Media-security

РАДУЖНЫЕ ИЗОБРАЖЕНИЯ В РЕАЛЬНОМ ВРЕМЕНИ

Н.Г.Власов, С.Д.Иванова

ВНИИ оптико-физических измерений,

103031, г.Москва, ул.Рождественка, 27.

1.Введение.

Радужные голограммы, в частности, тисненые на металлизированной пленке, стали популярными в последние годы. Благодаря способности восстанавливать яркие голографические изображения при освещении белым светом такие голограммы успешно используются в изобразительном искусстве, рекламе, декоративном оформлении товаров народного потребления, сувениров и т.п., а также для защиты от подделки документов и ценных бумаг.

В этой статье представлен метод получения радужных изображений без записи на регистрирующую среду, т.е. в реальном времени. Этот метод применим как для пропускающих фазовых объектов, так и для диффузно отражающих объектов.

2. Анализ основных уравнений радужной голографии.

Как известно, радужная голограмма, полученная по двухступенчатому или одноступенчатому методу, восстанавливает при когерентном освещении не только изображение записанного на нее объекта, но и изображение щели, ограничивающей спектр пространственных частот объектного волнового поля и восстанавливающейся в плоскости, в которой при просмотре находятся глаза наблюдателя.

Чтобы избежать непринципиальных в данном случае математических осложнений, рассмотрим два возможных случая размещения объекта по отношению к голограмме во время ее записи. В первом случае записывается изображение объекта, лежащее в плоскости голограммы (двумерный объект). Вывод уравнений (называемых основными уравнениями радужной голографии), описывающих этот случай, приведен в [1]. Во втором случае объект располагается достаточно далеко от голограммы, и можно показать (аналогично [1]), что основные уравнения радужной голографии имеют вид:

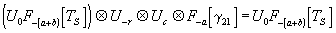(1)

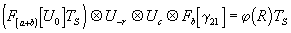(2)

где U_o - волновое поле вблизи объекта при его записи на голограмму, F_(a+b)[T_S] - обратное преобразование Френеля от функции пропускания щелевой апертуры T_S (индекс - (-(a+b)) означает расстояние от объекта (или его изображения) до щели (или ее изображения), присутствующее как параметр в обратном преобразовании Френеля), U_-r - волновое поле вблизи опорного источника при записи радужной голограммы, U_c - волнового поле вблизи восстанавливающего источника, F_a[g ₂₁] и F_b[g ₂₁] - соответственно обратное и прямое преобразования Френеля от комплексной степени когерентности g ₂₁ опорного и объектного волновых полей при записи радужной голограммы (индекс -a означает расстояние от объекта (или его изображения) до радужной голограммы, присутствующее как параметр в обратном преобразовании Френеля, а индекс b - расстояние от радужной голограммы до щели (или ее изображения), присутствующее как параметр в прямом преобразовании Френеля), F_(a+b)[U_o] -прямое преобразование Френеля от поля U_o, j (R) - cлучайное распределение волнового поля по пространственным координатам.

Левые части уравнения (1) и (2) описывают волновое поле в области восстановленного изображения объекта и в плоскости изображения щели соответственно. Правые части уравнения (1) и (2) описывают волновое поле в области локализации объектива и щели соответственно в процессе записи радужной голограммы. Таким образом, равенства (1), (2) обеспечивают необходимые условия получения радужного изображения объекта. Присутствие случайной функции j (R) в правой части уравнения (2) описывает возможность многостороннего наблюдения этого изображения.

Из уравнения (1), (2) можно вывести все известные способы записи радужных голограмм. Кратко поясним это для двух случаев - для диффузно отражающего и для фазового объекта. Волновое поле вблизи объекта можно записать как

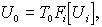(3)

где Т_о - функция отражения для отражающих объектов и функция пропускания для пропускающих объектов, F_i[U_i] - преобразование Френеля от поля U_i вблизи освещающего объект источника (при записи голограммы).

Для диффузно отражающего объекта уравнения выполняются за счет того, что функция отражения объекта Т_о ( а точнее, ее часть, описывающая микроструктуру поверхности объекта) является случайным распределением по пространственным координатам:

Т_о = j (R) (4)

Для фазового объекта случайной функцией является функция освещения U_i , т.к. фазовый объект освещается через матовое стекло, поэтому

F_i[U_i] = j (R) (5)

И в том, и в другом случае объектное и опорное волновые поля полностью когерентны, а опорный и восстанавливающий источники - точечные:

g ₂₁ = 1, U_-r = d (-r), U_c = d (c) (6)

Условия (4) - (6) обеспечивают выполнение уравнений (1), (2) для обычных схем записи радужных голограмм фазовых и диффузно отражающих объектов.

3. Новые методы получения радужных изображений.

Кроме того, анализ основных уравнений радужной голографии приводит к новым, не известным ранее способам получения радужных изображений в реальном времени. Рассмотрим получение радужного изображения фазового объекта с помощью схемы,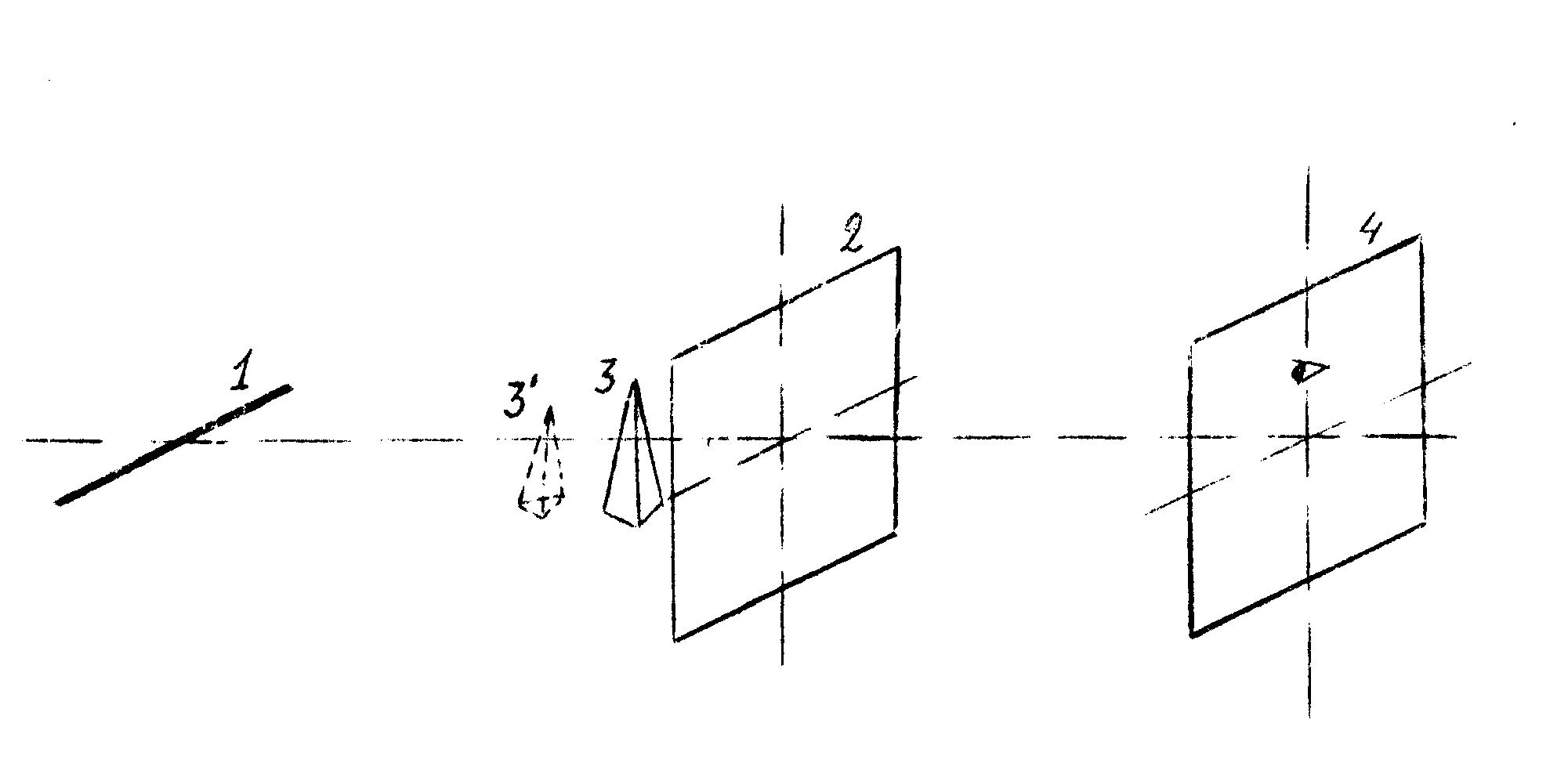

Рис.1 Получение радужного изображения фазового объекта. 1- линейный источник белого света, 2-голографическая линза, 3- фазовый объект, 3’- изображение объекта, 4-плоскость наблюдения

представленной на рис.1. Голографическая линза 2 строит действительное изображение линейного источника белого света 1 в плоскости наблюдения 4. Голографическая линза получена в результате регистрации интерференционной картины двух сферических волн (сходящейся и расходящейся), падающих под углом 30-40 градусов [2]. Изображение линейного источника ("щели"), размытое в радугу, образуется в плоскости 4. В первом порядке дифракции наблюдатель, находящийся в плоскости 4, видит мнимое радужное изображение, расположенное между линзой 2 и источником 1. Это фантомное изображение реального объекта, которое изменяет размеры и место локализации в зависимости от длины волны света, т.е. от положения глаз наблюдателя по вертикали, что само по себе является оригинальным оптическим эффектом.

Оптическая схема для получения радужных изображений реально присутствующих диффузно отражающих объектов подобна обычной одноступенчатой схеме записи радужных голограмм таких объектов. Отличие состоит лишь в том, что используется источник белого света и вместо регистрирующей среды в схеме присутствует дифракционная решетка (см. рис.2). Источник белого света 1 освещает диффузно отражающий объект 2, сферическая

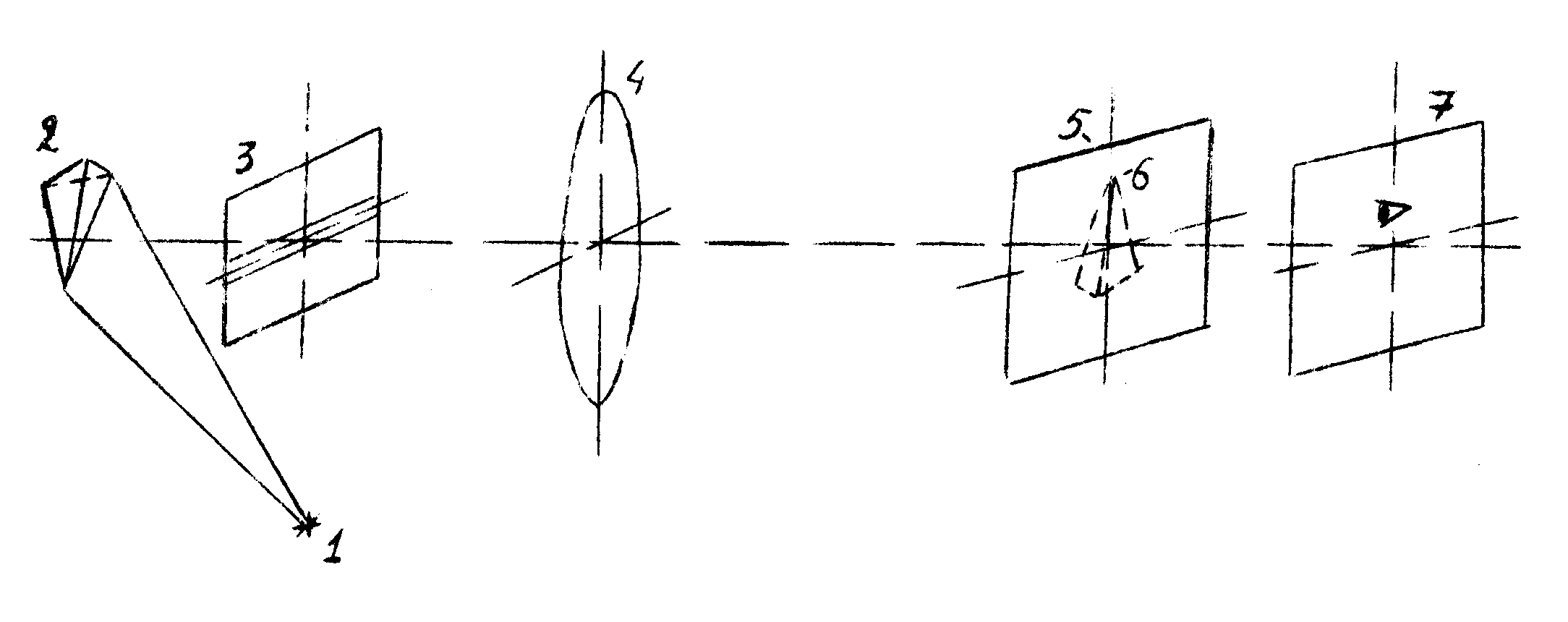
Рис.2 Получение радужного изображения диффузно отражающего объекта. 1-источник белого света, 2- диффузно отражающий объект, 3- щелевая диафрагма, 4- сферическая линза, 5- дифракционная решетка, 6- изображение объекта, 7- плоскость наблюдения.

линза 4 строит изображение объекта 6 вблизи дифракционной решетки 5, а щелевая диафрагма 3 находится между объектом 2 и линзой 4. Изображение щели, построенное в плоскости 7, размывается в радугу в вертикальном направлении. Глаз наблюдателя,

расположенного в плоскости 7, вырезает маленький участок спектра, и поэтому он видит радужное изображение объекта, как если бы оно было восстановлено с радужной голограммы. Недостаток данной схемы - потери света от источника на щелевой апертуре.

Описанные методы получения радужных изображений в реальном времени могут быть использованы для разработки голографических дисплеев, для создания оригинальных оптических эффектов, для моделирования схем записи радужных голограмм и в учебно-методических целях.

ЛИТЕРАТУРА

1.N.G.Vlasov, S.D.Ivanova, "Rainbow holography and its applicatijn", Proc. SPIE, v.1978, pp.361-367, 1993.

2. Н.Г.Власов, Г.В.Скроцкий, Е.Г.Соловьев, Квантовая электроника, №7, с.14-19, 1972.