Media-security

ГИБРИДНЫЕ ОПТИКО-ЦИФРОВЫЕ КОРРЕЛЯТОРЫ

С БИНАРНЫМИ ЧИСТО-ФАЗОВЫМИ ФИЛЬТРАМИ

НА ОСНОВЕ ЖИДКОКРИСТАЛЛИЧЕСКИХ ПВМС

В.В.Дадешидзе, И.Н.Компанец, И.Л.Линдунен, А.А.Васильев

В сравнении с голографическими согласованными фильтрами (ГСФ), как синтезированными на ЭВМ, так и записанными непосредственно в оптической системе, - бинарные чисто-фазовые фильтры (БЧФФ) позволяют существенно снизить требования к емкости памяти ЭВМ, используемой для синтеза и хранения фильтров, а также к разрешающей способности и динамическому диапазону ПВМС, используемых в Фурье-плоскости оптической системы пространственной фильтрации [1,2]..Кроме того, они обеспечивают минимальные потери света в оптической системе, более острый максимум функции корреляции и лучшее отношение максимума функции к ее боковым лепесткам, т.е. лучшее в сравнении с ГСФ отношение сигнал/шум в корреляционной плоскости.

Пониженные требования к емкости памяти позволяют использовать простейшие настольные ЭВМ для синтеза и хранения библиотеки фильтров, а бинарная функция пропускания делает возможным использование для их реализации практически любых фазовых либо амплитудных ПВМС.

Ранее сообщалось об использовании жидкокристаллических телевизионных (ЖК-ТВ) дисплеев [4,5], электрически управляемых магнитооптических модуляторов х6 , оптически управляемых ЖК-ПВМС фирмы Hugher [7] и ПВМС на основе деформируемых зеркал фирмы Texas Instruments [8] для формирования БЧФФ. В данной работе представлены результаты исследований оптико-цифровых корреляторов с БЧФФ на основе гибридного прибора, состоящего из ЭЛТ в сочетании с оптически управляемым ЖК-ПВМС [9,10] . Приведены основные соотношения, используемые при синтезе фильтров (раздел 2) и исследована зависимость параметров корреляционного отклика чисто-фазового фильтра от числа уровней квантования фазы (раздел 3). Даны оценки основных параметров устройства ЭЛТ-ЖК ПВМС, используемого для формирования БЧФФ (раздел 4) и приведены характеристики оптико-цифрового коррелятора с БЧФФ (раздел 5). Продемонстрирована возможность введения обратной связи для реализации адаптивных (нейроподобных) алгоритмов обработки изображений в гибридном корреляторе с БЧФФ (раздел 6).

2. Чисто-фазовые и бинарные чисто-фазовые фильтры.

Основные определения.

Для простоты рассмотрим одномерный случай. Комплексная передаточная функция фильтра, согласованного с сигналом f(x), определяется как F*(w ), где * обозначает комплексное сопряжение, F(w ) = A(w ) exp[j (w )] - фурье-образ сигнала f(x); A(w ),j ( w ) - амплитудная и фазовая составляющая спектра F(w ) соответственно [1,2] . Если на изображение наложен шум со спектральной плотностью мощности P(w ), то функция фильтра задается как F*(w )/P(w ) [2,11]. Очевидно, что функция пропускания H(w ) чисто фазового фильтра (ЧФФ) должна удовлетворять условию A(w )º 1, и, следовательно, H(w ) = exp[-ij (w )].

Чисто-фазовые фильтры (ЧФФ) можно рассматривать как комбинацию двух фильтров - согласованного A(w )exp(-ij (w ))/P(w ) и фильтра с пропусканием P(w )/A(w ), или в отсутствие шума 1/A(w ). Поскольку амплитуда спектра убывает с частотой, передаточная функция 1/A(w ) соответствует фильтру низких частот и в импульсном отклике h(x) ЧФФ изображения f(x) подчеркнуты контуры изображаемых объектов. Выделение контуров в опорном изображении приводит к обострению центрального лепестка функции корреляции f(x) * h(x) и одновременно к уменьшению ее боковых лепестков.

Бинарные чисто фазовые фильтры (БЧФФ) определяются как бинарное представление фазовой составляющей синусного [12] , или косинусного [13 фурье-образа, либо преобразования Хартли [14] сигнала f(x). Для описания БЧФФ удобно использовать бинарное представление действительной функции

F¢ = [ReF(w ) cosq - ImF(w )sinq ] в виде [11] :

H(w )=sgn[F¢ (w , q )] (1)

Угол q является пороговым значением фазы, при переходе через которое пропускание фильтра меняет знак, причем при q = 0 получаем бинарное представление синусного фурье-образа сигнала f(x): H(w ) = sgn[ReF(w )] , при q = p /2 - косинусного: H(w ) = sgn[ImF(w ) , а при q = p /4 - преобразования Хартли: H(w ) = sgn[ReF(w )-ImF(w )].

Фурье-образ действительной функции F’(w ) имеет четную амплитуду и нечетную фазу: f¢ (w ) = [exp(iq ) f(x) + exp(-iq ) f(-x) ; следовательно, импульсный отклик БЧФФ содержит два взаимно инвертированных импульсных отклика ЧФФ изображения, т.е.

два развернутых друг относительно друга на 180^o контурных изображения f. Расположение прямой и инвертированной компонент в импульсном отклике определяется положением изображения f при синтезе фильтра, а сдвиг фаз между ними - выбором угла q . Присутствие в импульсном отклике второго изображения приводит к появлению ложных максимумов в выходной плоскости. Так, например, для косинусного БЧФФ сигнал на выходе коррелятора

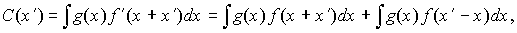(2)

содержит два слагаемых, первое из которых - искомая функция корреляции, а второе - свертка. Если при синтезе фильтра изображение располагалось в центре, то оба слагаемых в выражении (2) совмещены в пространстве и, следовательно, при q = 0 функции корреляции и свертки когерентно вычитаются, а при q = p /2 - складываются. Таким образом, выбор угла q влияет на отношение сигнал-шум (ОСШ) на выходе коррелятора [2,11].

Знакопеременная функция может быть реализована в виде фазовой модуляции транспаранта (сдвиг фазы света на p соответствует изменению пропускания от 1 до -1), либо путем добавления постоянной составляющей к функции амплитудного пропускания [15] . Во втором случае передаточная функция амплитудно кодированного БЧФФ (АКБЧФФ) равна 0,5[1 + H_Ф(w )] где H_Ф - передаточная функция БЧФФ. Сигнал на выходе коррелятора с АКБЧФФ:

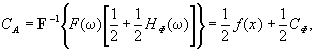(3)

содержит две составляющие: корреляционный отклик БЧФФ фильтра С_Ф и входное изображение f(x).Если при синтезе фильтра опорное изображение расположено в одном из квадрантов входной плоскости, то корреляционный пик и восстановленное изображение пространственно разнесены.

3. Число уровней квантования фазы и параметры ЧФФ

Присутствие инвертированной копии входного сигнала в импульсном отклике БЧФФ, возникающее из-за бинаризации фазы, приводит к дополнительным вариациям амплитуды пика функции корреляции и росту уровня ее боковых лепестков. Это, в свою очередь, приводит к снижению отношения сигнал-шум на выходе коррелятора в сравнении с ОСШ коррелятора с ЧФФ [1,11]. Известно, что при увеличении числа N уровней квантования

фазы ОСШ на выходе ЧФФ растет как sinc² (1NТ) [16]. Однако при этом ОСШ оценивалось как отношение среднего значения интенсивности пика корреляции к дисперсии амплитуды пика при наличии на входе коррелятора белого шума, что существенно для измерения интенсивности (амплитуды) корреляционного сигнала. Не менее важными критериями оценки качества корреляторов с ЧФФ являются: отношение интенсивностей (амплитуд) пика функции корреляции и ее боковых лепестков (ОПБЛ) - используется наряду с ОСШ для оценки шумов, поскольку определяет вероятность правильного обнаружения сигнала на выходе коррелятора); острота максимума функции корреляции, измеряемая как отношение энергии пика к суммарной энергии боковых лепестков; доля энергии падающего света, приходящаяся на корреляционный пик (эффективность использования света в схеме коррелятора) [11,17,18].

Для оценки параметров ЧФФ с различным числом уровней квантования фазы в численном эксперименте использовалось изображение размером 64*32 элемента, содержащее 8 градаций серого тона (Рис.1а). Доля энергии, приходящаяся на четную часть изображения (эффективно присутствует в косинусном БЧФФ):

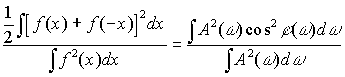(4)

составляла 0,86. Бинаризованный по уровню 0,5 от максимального значения импульсный отклик ЧФФ с различным числом уровней квантования фазы показан на Рис. 1б. При N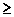2 уровнях квантования фазы функция пропускания фильтра j (w ) принимала значение 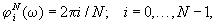если 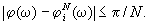При N= 2 формировался косинусный БЧФФ (q = 0), поскольку он, как правило, обеспечивает максимальное ОСШ для вещественных сигналов [11].

Табл.1. Сравнительные характеристики ЧФФ с различным числом квантования фаз.

N	2	4	8	256
I_max ОСШ g	0,39 287 0,038	0,83 1194 0,085	0,96 1241 0,098	1 1476 0,104

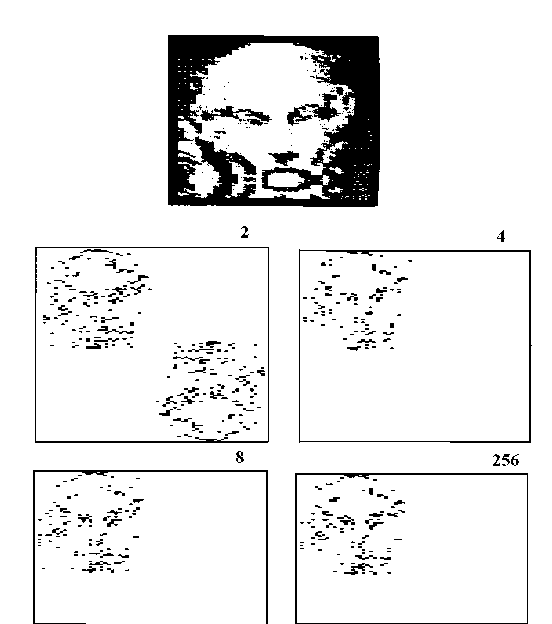
Рис. 1. а) Исходное изображение, использованное для синтеза N-

уровневых фильтров в численном эксперименте; б) бинаризованный по уровню 0б5 от максимального значения импульсный отклик ЧФФ с числом уровней квантования фазы N = 2; 4; 8; 256.

В Табл. 1 приводятся значения амплитуды пика С_max, отношения интенсивностей пика и боковых лепестков и остроты пика функции корреляции для ЧФФ изображений, расположенных в одном из квадрантов входной плоскости. Острота пика g вычислялась в виде [17] :

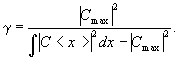(5)

Как видно из Табл. 1 корреляционный отклик ЧФФ снижается на 4% при 8 уровнях квантования фазы, на 20% - при 4 уровнях и более чем на 50% - для косинусного БЧФФ. Это подтверждает целесообразность использования в ЧФФ более чем двух уровней квантования фазы [11,16,18]. Действительно, ЧФФ с ограниченным числом уровней квантования фазы (N = 4 - 8), занимая промежуточное положение между ЧФФ с непрерывным фазовым пропусканием и БЧФФ, позволяют сократить в 5 - 6 раз объем хранимой информации без существенного ухудшения корреляционных характеристик фильтра.

4. Интерфейс ЭЛТ-ЖК ПВМС для ввода изображений и фильтров в оптический коррелятор

Для ввода изображений и формирования пространственных фильтров в оптической части гибридного оптико-цифрового коррелятора использовался ЖК ПВМС типа МДП-ЖК, на вход которого поступало изображение с волоконно-оптического экрана малогабаритной ЭЛТ с диаметром экрана 20 мм. В устройстве ввода изображений волоконно-оптическая пластина (ВОП) на входе ПВМС находилась в непосредственном контакте с ВОП-экраном ЭЛТ. Спектральная характеристика экрана ЭЛТ имела максимум на длине волны 628 нм, которая лежит в диапазоне фоточувствительности МДП структуры на GaAs. Амплитудная либо фазовая модуляция отраженного считывающего света достигалась за счет гибридного эффекта в закрученной на 45^o структуре нематического ЖК [3]. Устройство, принцип действия и характеристики ЖК ПВМС, в том числе - в сочетании с ЭЛТ (ЭЛТ-ЖК ПВМС), подробно описаны в литературе [3,9,10].

Бинарные и многоуровневые изображения, соответствующие фазовым профилям формируемых фильтров, рассчитывались на персональной ЭВМ PC/AT-286 и хранились на жестком диске. Для вывода изображений из ЭВМ использовался интерфейс, формирующий взвешенную сумму цифровых сигналов, поступающих с выхода видеоадаптера EGA, который в графическом

режиме обеспечивал формат 640*200 элементов разложения, совместимый с телевизионным стандартом.

Телевизионное изображение поступает на вход ПВМС со стороны полупроводника (GaAs), создавая потенциальный рельеф на границе с ЖК. Считывающее излучение He-Ne лазера подается с противоположной стороны ПВМС и дважды проходит через слой ЖК, отражаясь от зеркала внутри ПВМС. Считывающий свет поляризован параллельно директору на передней границе слоя ЖК, поэтому начальное пропускание ячейки определяется только оптической активностью закрученной структуры и поляризация отраженного света на выходе ПВМС совпадает с исходной [3]. При деформации структуры под действием электрического поля одновременно с изменением двойного лучепреломления слоя ЖК происходит раскрутка спирали, что приводит к повороту плоскости поляризации [19] и к появлению составляющей электрического вектора, ортогональной исходному направлению [3,20].

Гибридный ориентационный эффект, также как и S-эффект в планарно ориентированном слое ЖК [3], позволяет реализовать непрерывные профили фазового пропускания за счет сдвига фазы необыкновенного луча при изменении угла наклона молекул ЖК под действием электрического поля [3,20]. Однако недостаточная глубина модуляции фазы отраженного света из-за ограниченности интенсивности видеоизображения, поступающего с экрана ЭЛТ, не позволила получить сдвиг фазы на 2p между освещенными и темными участками апертуры модулятора, необходимый для формирования N-уровневых функций фазового пропускания. Тем не менее, для реализации биполярной функции пропускания (A; -A; A<1) можно использовать эффект поворота плоскости поляризации отраженного света при изменении напряжения на слое ЖК [19]. В этом случае ось анализатора должна располагаться перпендикулярно биссектрисе угла j , образованного азимутами поляризации неосвещенных и освещенных участков ПВМС.

Измерения показали, что при максимальном контрасте бинарного входного изображения и оптимальном режиме ПВМС (напряжение питания 18 В, частота 2 кГц) угол j » 40^o . В самом деле, при повороте оси анализатора на угол f » 20^o против часовой стрелки приводил к переходу от двухполярной к однополярной (неотрицательной) функции с максимальным амплитудным контрастом [19] . Таким образом, поворот анализатора на угол о соответствует переходу от БЧФФ к АКБЧФФ. Заметим,

что пропускание БЧФФ, также как пропускание освещенных участков АКБЧФФ, определяется законом Малюса: I = I_o sin² (j /2), где I_o - пропускание поляризаторов с учетом потерь света в ЖК ячейке. В нашем случае I @ 0,12 I_o .

На Рис.2 приведено изображение импульсного отклика АКБЧФФ изображения буквы G. Поскольку при синтезе фильтра

Рис. 2. Импульсный отклик амплитудно-кодированного БЧФФ изображения буквы G.

изображение размещалось в одном из квадрантов входной плоскости, импульсный отклик представляет собой два пространственно разнесенных и повернутых друг относительно друга на 180^o контурных изображения G и яркое пятно в центре выходной плоскости, соответствующее постоянному смещению в выражении (3).

5. Оптический коррелятор с БЧФФ.

Экспериментальная схема оптико/цифрового коррелятора представлена на Рис. 3. Исходное изображение воспринимается видеокамерой VDС1 и с экрана малогабаритного кинескопа СRT1 поступает на вход первого ЖК ПВМС (LCSLM1). Входное изображение считывается коллимированным пучком света He-Ne лазера. Пространственный фурье-спектр входного изображения формируется фурье-объективом FTL1. Увеличенное изображение фурье-спектра переносится микрообъективом mL на выходную плоскость второго ЖК ПВМС (LCSLM2), который формирует функцию пропускания фильтра. Функция корреляции (обратное преобразование Фурье) формируется в фокальной плоскости второго фурье-объектива FTL2 и проецируется с увеличением микрообъективом mL2 на мишень видеокамеры VDC2. С ее выхода изображение корреляционной плоскости поступает в ЭВМ через интерфейс ввода телевизионных изображений.

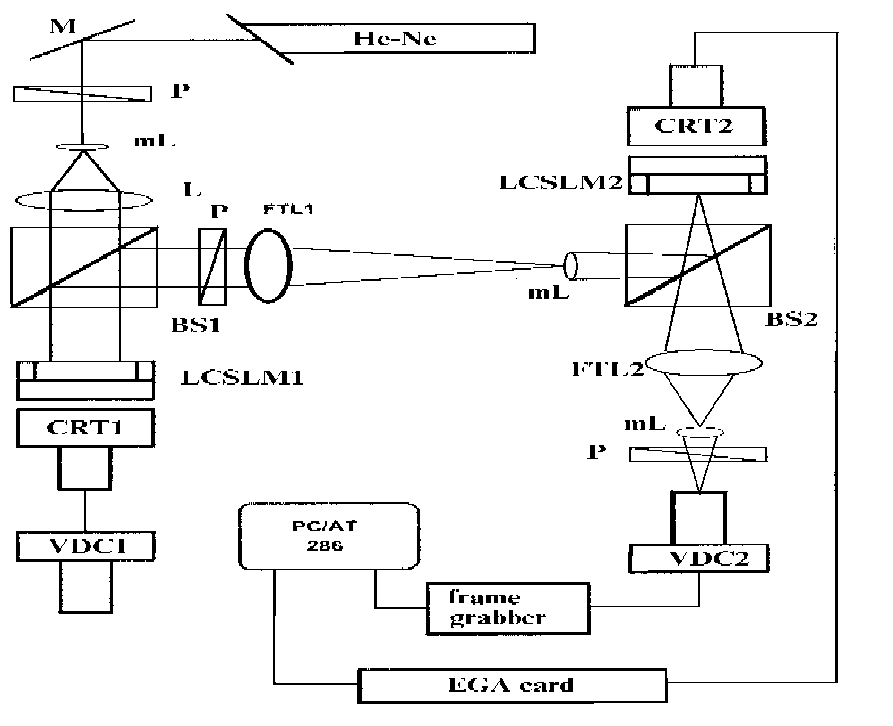
Рис. 3. Экспериментальная схема оптического коррелятора с БЧФФ: M-

зеркало; P - поляризатор; BS - светоделитель; FTL - фурье-объектив;

mL - микро-объектив; CRT - ЭЛТ; LCSLM - ЖК ПВМС; VDC - видеокамера;

ЧФФ размером 128*64 элементов последовательно выводились на экран CRT2 в виде массивов прямоугольников различной интенсивности. Шкала интенсивностей содержала 8 уровней серого тона, полученных путем суммирования с соответствующими весами цифровых RGB сигналов видеоадаптера EGA.

Изображение корреляционной плоскости для БЧФФ слова "SAGE", полученное в экспериментальной схеме и при численном расчете, показано на Рис. 4. При сдвиге изображения фильтра в один из квадрантов входной плоскости функции корреляции и

свертки оказываются пространственно разделенными. Как было показано в п.2, если опорное изображение при синтезе фильтра находится в центре, то выбор синусного или косинусного преобразований приводит к когерентному вычитанию или сложению корреляционной и сверточной составляющих. Рис. 5 содержит изображения корреляционной плоскости для косинусного и синусного БЧФФ центрированного изображения буквы "O", полученные в эксперименте.

Минимальное время вычисления двумерной корреляционной функции, без учета времени обработки и считывания фильтра, составляет 120 мс. Из них 40 мс затрачивается на вывод фильтра и 80 мс составляет время ввода в ЭВМ. Для повышения скорости смены фильтров их изображения записывались с чередованием в различные страницы видеопамяти. Измерения временного отклика коррелятора показали, что система может работать с частотой смены фильтров до 8 Гц без ухудшения выходных параметров.

Построчный вывод изображений БЧФФ приводит к осцилляциям с частотой кадровой развертки оптического отклика в освещенных участках ЖК ПВМС. Это вносит существенный вклад во временную нестабильность пика корреляционной функции, в особенности - при отсутствии взаимной синхронизации разверток видеокамер и ЭЛТ. Непосредственные измерения показали, что нормированное среднеквадратичное отклонение величины корреляционного максимума составляет 6%. Эту величину можно считать суммарной погрешностью вычисления корреляционной функции.

На выходе видеоадаптера EGA формируется изображение БЧФФ с различным масштабом по вертикали и горизонтали. Для используемого графического режима EGA (640*200 точек) аспектное отношение (Aspect Radio) равно 042. Однако фактическая разница масштабов по вертикали и горизонтали зависит в большей степени от амплитуд тока в отклоняющих катушках ЭЛТ. Аппаратная корректировка горизонтального и вертикального масштаба может производиться оптически с помощью цилиндрических линз либо путем регулировки размера кадров и строк на экране ЭЛТ. Другая возможность состоит в программном корректировании размеров фильтра. Программа с независимой линейной интерполяцией по двум координатам позволила подобрать необходимое соотношение сторон выводимых элементов БЧФФ (экспериментально подобранное значение составило 0,37) и обеспечить точное совпадение масштабов фильтра и фурье-спектра входного изображения.

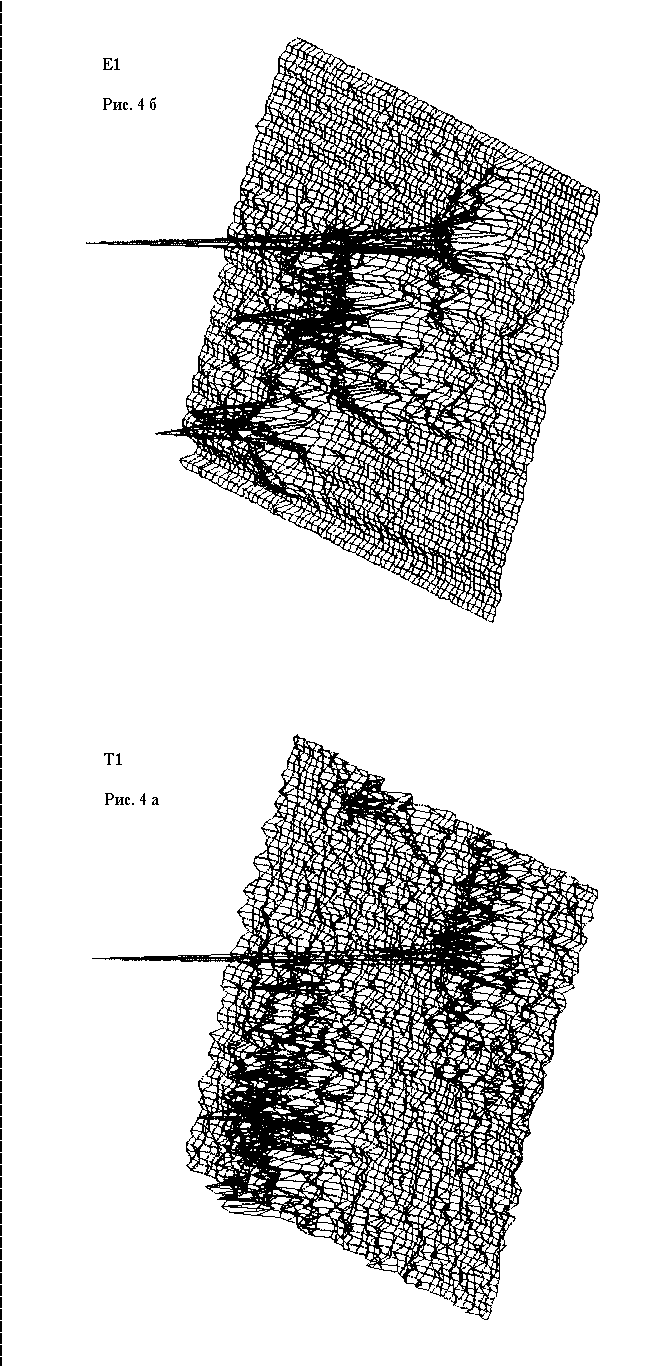Рис. 4 Изображение выходной плоскости коррелятора с БЧФФ: а - численный расчет; б - экспериментальный результат.

Дискретный характер БЧФФ, формируемых с использованием ПВМС, приводит к ограничению размеров входного и опорного сигналов, которые не могут быть больше чем l f/a , где a - расстояние между элементами фильтра, l - длина волны, f - фокусное расстояние Фурье-объектива [21]. Кроме того, дискретная структура фильтра приводит к репликации импульсного отклика [5,21] и, следовательно, к появлению ложных максимумов-двойников в функции корреляции [21]. Последний недостаток может быть ослаблен при использовании оптически управляемого ПВМС в частотной плоскости коррелятора если расстояние между элементами фильтра выбирается равным размеру элемента. В самом деле, функцию пропускания фильтра можно представить в одномерном случае как [21]:

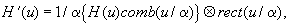(6а)

где символом 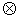обозначена операция свертки, u=x₂ / l f - пространственная частота, ч координата в плоскости фильтра, l и f - длина волны и фокусное расстоянию Инверсное Фурье преобразование последнего выражения есть:

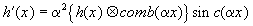(6b)

Функция (6b) содержит реплики импульсного отклика с центрами в точках x_m = m/a , m = 0, ± 1, ± 2,...(выражение в фигурных скобках). В тех же точках x_m расположены нули функции sinс(a x)=(1/p x)sin(p a x) для m ¹ 0 , которые ослабляют боковые порядки импульсного отклика (6а). Огибающая функция sinс в выражении (6b) приводит к тому, что отклик неинвариантен к выбираемому положению изображения при синтезе фильтра. Чем дальше опорное изображение от центра, тем слабее корреляционный отклик. На Рис.6 показана зависимость интенсивности корреляционного пика от сдвига изображения относительно центра входного окна при синтезе БЧФФ. С другой стороны, на этапе фильтрации значения корреляционных коэффициентов инвариантны к положению изображения в исходной сцене. Формула (6.а) справедлива при условии, что ПВМС точно воспроизводит апертурную функцию пропускания одного элемента. Это выполняется при a >>d , где - ширина функции рассеяния линии (ФРЛ), определяющая разрешающую способность ПВМС [3]. Для учета влияния разрешающей способности ПВМС необходимо умножить импульсный отклик фильтра (6.a) на функцию передачи модуляции (ФПМ) ПВМС, которая равна фурье-образу ФРТ.

Рис. 5. Изображения корреляционной плоскости для косинусного и синусного БЧФФ изображения буквы "О", полученные в эксперименте.

Рис .6. Амплитуда корреляционного максимума на выходе коррелятора в зависимости от положения опорного изображения при синтезе фильтра: ^х-сдвиг влево; + - сдвиг вверх; - сдвиг по диагонали

Влияние (ФПМ) ПВМС приводит к более быстрому чем sinс спаду интенсивности максимума пика корреляции в зависимости от сдвига эталонного изображения при синтезе фильтра. Разрешение

ПВМС (4 лин/мм по полуспаду ФПМ) являлось достаточным для используемых размеров БЧФФ. Из графиков рис. 6 видно, что отклик фильтра уменьшается в два раза при сдвиге изображения примерно на 52 элементов при теоретическом значении 56 для полуспада функции sinс² . Осцилляции отклика фильтра в зависимости от сдвига эталонного объекта объясняются погрешностью воспроизведения функции фильтра за счет конечного размера элемента a .

6. Адаптивный нейроподобный коррелятор с БЧФФ.

Адаптивные оптические системы на основе корреляторов с обратной связью и с нелинейностью в корреляционной/предметной [22,23] и в частотной [23,24] плоскостях могут рассматриваться как нейропроцессоры, пригодные для решения задач распознавания образов, восстановления сигналов, ассоциативного поиска и

реконструкции изображений [22-24]. Успешная работа таких систем определяется их способностью подавлять ложные корреляционные сигналы-помехи (высокое отношение сигнал-шум) и выявлять сходство входного сигнала с одним из хранимых в памяти

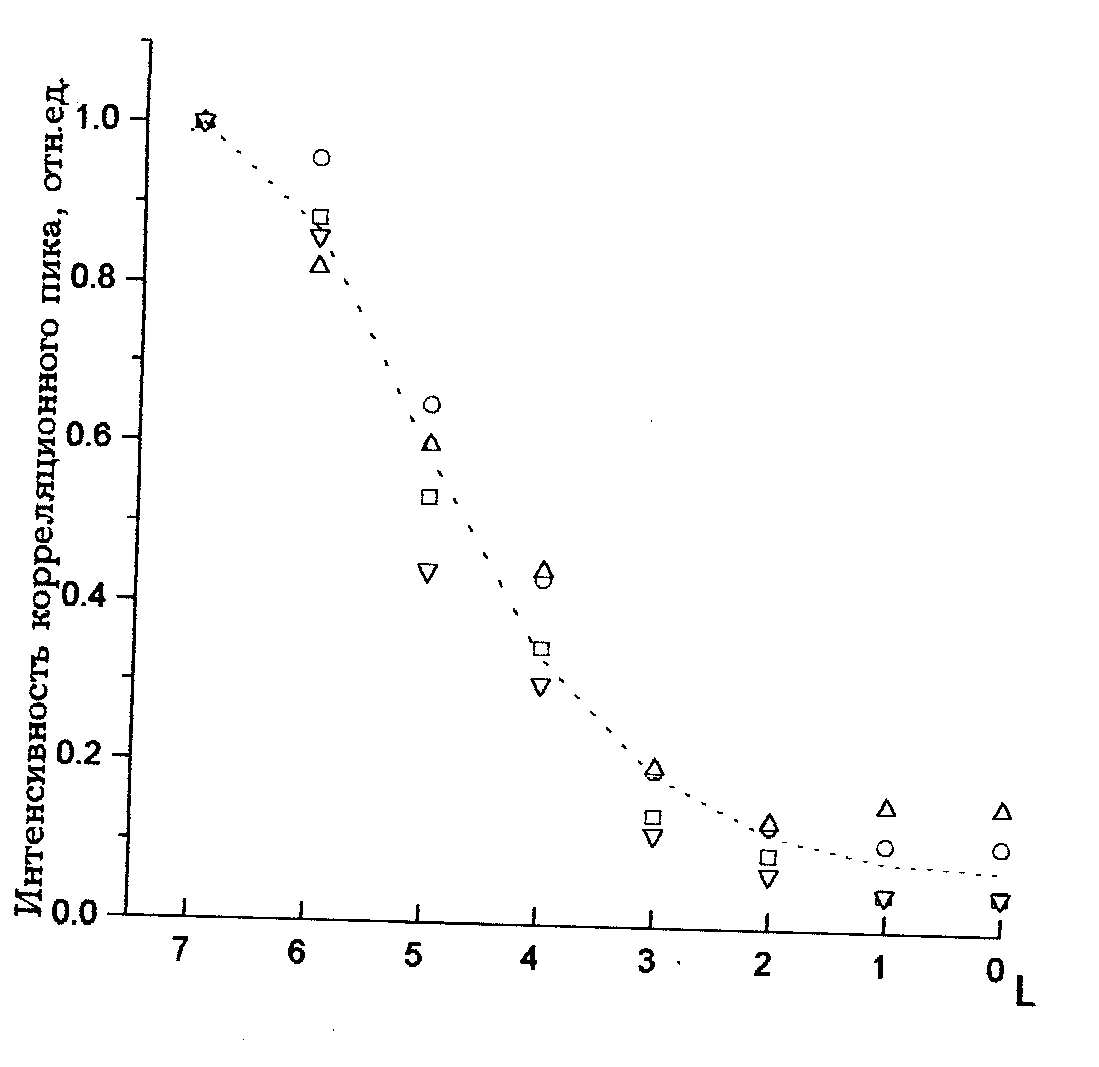
Рис. 7. Зависимость корреляционных максимумов от уровня яркости экрана ЭЛТ.

эталонов (минимальная вероятность ошибки). Выполнение этих условий обеспечивает существование устойчивых состояний системы, соответствующих набору хранимых эталонов и высокую скорость сходимости при попадании входного сигнала в область "притяжения" одного из эталонов. С этой точки зрения представляет интерес использование БЧФФ в частотной плоскости адаптивного коррелятора, поскольку эти фильтры обеспечивают высокое отношение величины пика функции корреляции к ее боковым лепесткам и обладают повышенной дискриминационной способ. ностью [11,18].

Адаптивный режим работы коррелятора был реализован непосредственно в схеме, изображенной на рис. 3. Библиотека опор-

ных изображений представлена на Рис. 8а. В видеопамяти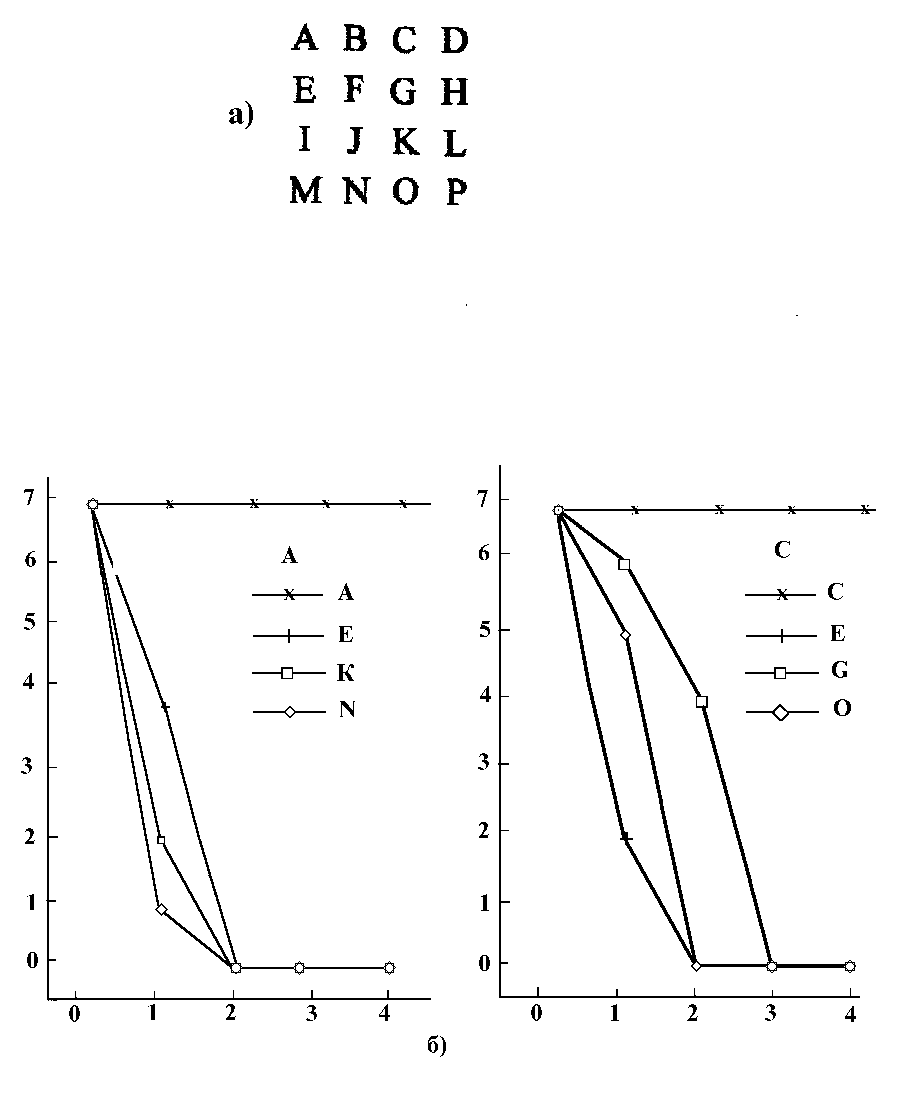

Рис. 8. а) Опорные изображения, использованные при синтезе библиотеки БЧФФ; б) Изменение уровня яркости изображений фильтров, выводимых на экран ЭЛТ в зависимости от числа итераций.

адаптера EGA объемом 256 K хранилось одновременно до 16 БЧФФ, скорректированных по вертикальному и горизонтально-

му масштабам. Выбор нужного фильтра и уровня выходного видеосигнала достигался перекодированием карты памяти УПФ. Значения корреляционных максимумов, полученные на выходе коррелятора, образуют вектор K, компоненты k_i которого нормировались на соответствующие значения максимума функции автокорреляции:

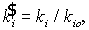где 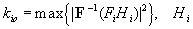- БЧФФ функции f_i. Далее вектор 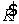приводился к единичному виду 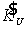путем нормировки на max{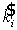}. В последующих итерациях светлые элементы в изображениях фильтров, соответствующие значениям H_i=-1, представлялись одним из восьми уровней серого тона (j=0,...7) в соответствии со значением 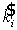, полученным в предыдущей итерации. Так, если 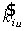попадает в интервал [0,125 f; 0,125(f+1)], то для представления элементов фильтра с H_i = -1 используется j-й уровень серого тона. Таким образом, эффективность и величина отклика уменьшались для тех фильтров, для которых 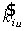<0,875.

Конкретный вид нелинейности в канале обратной связи задавался характеристической кривой ПВМС фильтра H(I_j) = sin² [D Ф(I_j )/2], где I_j - интенсивность (яркость экрана ЭЛТ), соответствующая j-му уровню серого тона; фазовая задержка для двух ортогональных поляризаций света, прошедшего через ЖК D Ф(I) @ a tanh(bI), a и b - параметры ПВМС, зависящие от чувствительности фотопроводника и анизотропии ЖК [3]. 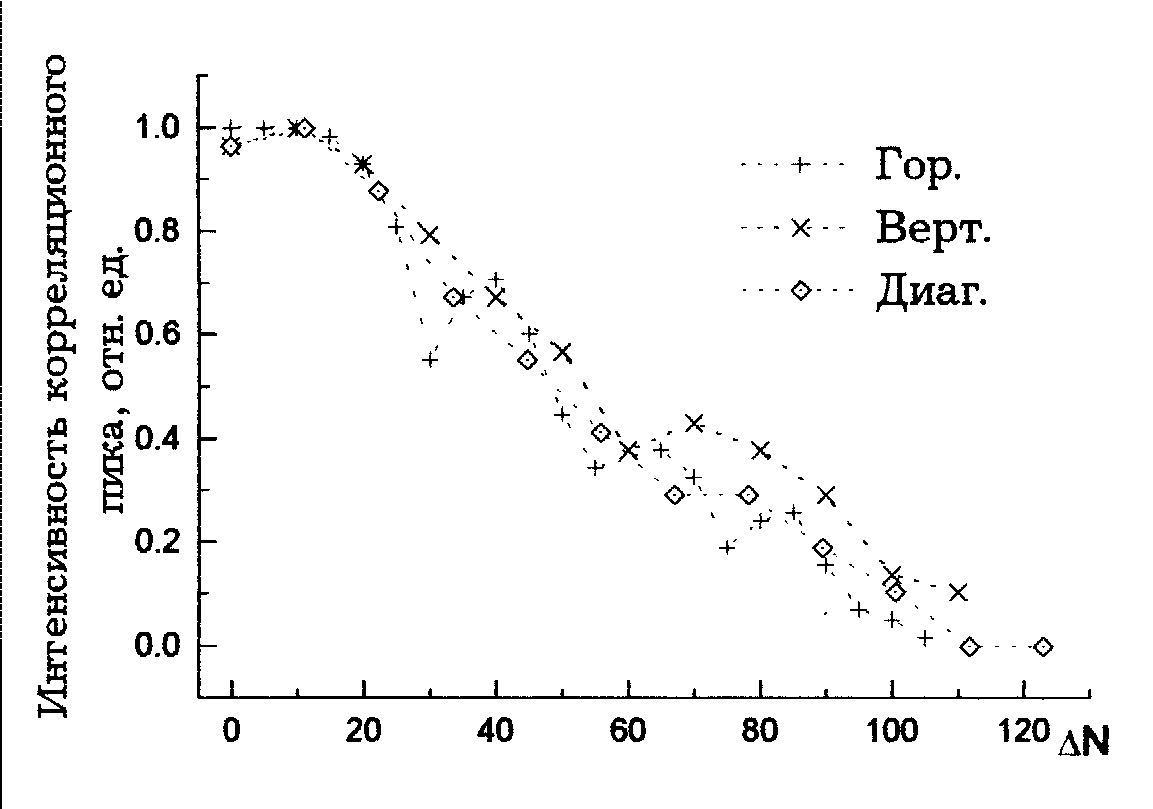Управляющее напряжение на ПВМС фильтра и положение анализатора устанавливались так, чтобы сдвиг фаз между элементами фильтра с j = 0 и j = 7 ("черные" и "белые" участки соответственно) составлял p рад. На Рис. 7 приведена зависимость интенсивности корреляционных максимумов от уровня яркости j в изображении на экране ЭЛТ. Таким образом схема, изображенная на Рис. 3, превращается в адаптивную систему с нелинейной обратной связью, в которой регулируемым параметром является глубина амплитудно-фазовой модуляции функции пропускания БЧФФ. Система приходит в устойчивое состояние, когда вектор 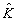содержит единственную составляющую, отличную от нуля.

Нормировка корреляционных коэффициентов на 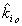позволяет учесть долю входного изображения в опорном. При этом система уверенно различает изображения таких букв как С, O, G или F, E, B и т.д. Однако особенности системы таковы, что изображения букв D, E, F, P и др., содержащих вертикальную черту, при этих условиях идентифицировались как I. Эту проблему удалось решить путем преобразования весовых коэффициентов к виду [1+ h ln]. 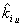Результаты экспериментов показали, что существуют такие значения h , при которых система сходится к моно- или мультистабильным состояниям при заданном режиме работы ПВМС фильтра. Так при 0,005 < h < 0,03 система устойчиво сходится к истинным эталонам для всех входных изображений из набора Рис. 8а. Скорость сходимости составляла 3 - 6 итераций, что обусловлено значительной крутизной функции нелинейности H(I_j ). На Рис. 8.б приведены графики сходимости для некоторых букв при входных изображениях букв С и I.

7. Заключение.

Результаты численного моделирования и экспериментальных исследований показали возможность эффективного использования жидкокристаллических оптически управляемых ПВМС, соединенных через волоконную оптику с малогабаритным кинескопом, как для ввода изображений, так и для формирования бинарных чисто-фазовых фильтров в гибридном оптико-цифровом корреляторе. Несмотря на сравнительно невысокую разрешающую способность использованного в работе гибридного прибора ЭЛТ-ЖК ПВМС, он обладает целым рядом достоинств, таких как отсутствие дискретной структуры элементов и возможность получения непрерывной (многоуровневой) функции фазового и амплитудного пропускания, которые делают его привлекательным и перспективным для использования в практических системах оптической обработки данных, включая нейроподобные нелинейные системы с обратной связью.

Авторы выражают благодарность Р.М.Саввиной и В.И.Труфану за предоставление образцов ПВМС, В.Н.Полубоярову - за предоставление модуля ЭЛТ, а также С.Н.Верескову и Н.А.Васильеву - за полезные консультации и помощь в проведении экспериментов.

Литература

1. D.L.Flanntery and J.L.Horner,"Fjurier optical signal processing". Proc.IEEE, vol.77, № 10, pp. 1511-1527, October 1989.

2. B.V.K.Vijaya Kumar, "Tutorial survey of composite filter designs for optical correlators", Appl.Opt., vol.31, № 23, pp. 4773-4801, August 1992.

3. А.А.Васильев, Д.Касасент, И.Н.Компанец, А.В.Парфенов. Простран ственные модуляторы света. - М.: Радио и связь, 1987, 320 с.

4. T. H. Barnes, T. Eiju, K. Matsuda, and N. Ooyama, "Phase-only modulation using a twisted nematic liquid crystal television," Appl. Opt., Vol.28, No.22, pp.4845-4852, November 1989.

5. J.-J. P. Drolet, L. Leclerc, Y. Cheng, H. Arsenault, Real-time binary phase-only circular harmonic filter using a liquid crystal television in the Fourier plane of an optical correlator," Opt. Eng., Vol.31, No.5, pp.939-946, May 1992.

6. D. L. Flannery, A. Biernacki, J. Loomis, and S. Cartwright, "Real-time coherent correlator using binary magnetooptic spatial light modulators at input and Fourier planes,"Appl. Opt., vol.25, No.4, p.466, February 1986.

7. J. A. Davis, G. M. Heissenberger, R. A. Lilly, D. M. Cottrell, and M. F. Brownell, "High efficiency optical reconstruction of binary phase-only filters using the Hughes liquid crystal light valve," Appl. Opt., Vol.26, No.5, pp.929-933, March 1987.

8. J. M. Florence and R. O. Gale, "Coherent optical correlation using a deformable mirror device spatial light modulator in the Fourier plane," Appl. Opt., Vol. 27, pp. 2091-2093, 1988.

9. A. A. Vasiliev, V.V.Dadeshidze, and I. N. Kompanets, Lebedev Physical Institute, Preprint 23, Moscow, 1991.

10. A. A. Vasiliev, V.V.Dadeshidze, and I. N.Kompanets, "Binary phase-only filters generated in a hybrid TV-LC spatial light modulator," ICO-92 Meeting on Optical Computing (Minsk, Belo russia, June 1992), 29E32. 11. B. V. K. Vijaya Kumar, "A tutorial review of partial-information filter designs for optical correlators," Asia-Pacific Eng. J. (Part A), Vol.2, No.2, pp.203-215, 1992.

12. J.L.Horner, J.R.Leger. "Pattern recognition with binary phase only filters," Appl. Opt., Vol.24, No.5, pp.609-611, March 1985. 13. D. Psaltis, E. G. Paek, and S. S. Venkatesh, "Optical image correlation with a binary spatial light modulator," Opt. Eng., Vol.23, pp.698-705, Nov.-Dec. 1984.

14. D. M. Cottrell, R. A. Lilly, J. A. Davis, and T. Day. "Optical correlator performance of binary phase-only filters using Fou rier and Hartley transforms," Appl. Opt., Vol.26, No.18, pp.3755-3761, October 1987.

15. M. A. Flavin and J. L. Horner. "Amplitude encoded phase-only filters," Appl. Opt., Vol.28, No.9, pp.1692-1696, May 1989.

16. B. V. K. Vijaya Kumar and J. M. Connelly, Effects of quantazing the phase in correlation filters," Proc. SPIE, Vol. 1151, pp.166-173.

17. J. D. Downie and M. B. Reid. "Mapping considerations for opti mal binary correlation filters," Appl. Opt., Vol.29, No.35, pp.5235-5241, December 1990.

18. Ph. Refregier, B. V. K. Vijaya Kumar, and C. Hendrix, "Multi criteria optimal binary amplitude phase-only filters," J. Opt. Soc. Am.-A, Vol.9, No.12 pp.2118-2125, December 1992.

19. J. A. Davis, G. A. Heissenberger, R. A. Lilly, D. M. Cottrell, and M. F. Brownell, "High efficiency optical reconstruction of binary phase-only filters using the Hughes liquid crystal light valve," Appl. Opt., Vol.26, No.5 pp.929-933, March 1987.

20. N. Konforti, E. Marom, S.-T. Wu, "Phase-only modulation with twisted nematic liquid-crystal spatial light modulators," Opt. Letters, Vol.13, No.3, pp.251-253, March 1988.

21. S. P. Kozaitis, W. E. Foor, "Optical correlation using reduced resolution filters," Opt. Eng., Vol.31, No.9, pp.1929-1935, September 1992.

22. Y. Owechko, G. J. Dunning, E. Marom, and B. H. Soffer, "Holo graphic associative memory with nonlinearities in the correla tion domain," Appl. Optics, Vol.26, No.10, pp.1900-1910, May 1987.

23. N. Kasama, Y. Misuoka, T. Iwaki, S. Yamamoto, "Effects of non linear parameters in feedback joint-transform correlator (FJTC) (1)," Proc. SPIE, Vol.1772, pp.51-62, July 1992. (1),

24. B. Javidi and J. Wang, "Optical associative processor with variable nonlinearities in the filter plane," Opt. Eng. Vol.31, No.9, pp.1990-1998, September 1992.