БИНАРНЫЕ ФАЗОВЫЕ ФИЛЬТРЫ КРУГОВЫХ
ГАРМОНИЧЕСКИХ
СОСТАВЛЯЮЩИХ,
ИНВАРИАНТНЫЕ К ОРИЕНТАЦИИ ИЗОБРАЖЕНИЙ.
В.В.Дадешидзе, А.Г.Дворядкин, И.Н.Компанец, И.Л.Линдунен.
1.
Введение.
Оптические корреляторы, реализующие корреляционную функцию
сравнения изображения и эталона для автоматического распознавания
изображений, хорошо известны [1,2] . Использование в корреляторах
чисто фазовых фильтров (ЧФФ) [3,4] , содержащих только фазовую
составляющую комплексных согласованных фильтров, позволяет
получать более высокие и острые максимумы корреляционной
функции, что увеличивает точность принимаемых решений. Частным
случаем оптических ЧФФ являются бинарные чисто фазовые фильтры
(БЧФФ), у которых фаза принимает только два значения, отличающиеся
на 180o . Отображение оптических БЧФФ в реальном
времени может производиться с использованием устройств с
ограниченным динамическим диапазоном, таких как жидкокристаллические
дисплеи [5[ , магнитооптические [6] или жидкокристаллические
модуляторы света [7] , устройства с деформируемым зеркалом
[8] .
ЧФФ и БЧФФ дают более высокий относительный вклад высоких
пространственных частот в максимум корреляционной функции
по сравнению с согласованными фильтрами, что приводит к
более быстрому исчезновению корреляционного отклика при
несовпадении ориентации изображения и эталона. Одним из
возможных методов устранения этого недостатка корреляторов
является использование фильтров круговых гармонических составляющих
(КГС) [9] , обладающих инвариантностью к ориентации изображений.
Метод синтеза БЧФФ посредством бинаризации фазовой составляющей
согласованного фильтра может быть аналогично использован
для синтеза БЧФФ КГС [10,11] . В данной работе приводится
анализ особенностей синтеза БЧФФ КГС, а также экспериментальные
результаты реализации таких фильтров в оптическом корреляторе
с жидкокристаллическими модуляторами света.
2.
Фильтры круговых гармонических составляющих.
Изображение f(x,y), или в полярных координатах fo
(r,q ) может быть представлено в виде суммы гармонических
составляющих [9] :
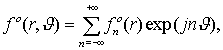 (1)
(1)
где
 (2)
(2)
Величина
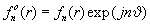 называется
n-й КГС изображения f(x,y).
называется
n-й КГС изображения f(x,y).
Значение корреляционной функции повернутого на угол a
изображения 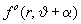 и k-й КГС в точке с координатами (0,0) равно:
и k-й КГС в точке с координатами (0,0) равно:
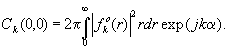 (3)
(3)
Как следует из последнего выражения б интенсивность регистрируемого
сигнала |Сk (0,0)|2 не зависит от
ориентации входного изображения.
При
произвольном выборе положения центра полярных координат,
относительно которого производится разложение (1), значение
выражения (3) не является максимальным из всех возможных
значений, получаемых для различных центров разложения. Это
приводит к ошибке при определении координат объекта б поскольку
положение максимума корреляционной функции не совпадает
с центром разложения. Положение центра полярных координат
б для которого максимум корреляционной функции находится
в точке (0,0), называется центром соответствия (ЦС) КГС.
Если разложение (1) осуществлялось относительно ЦС, то выполняется
условие:
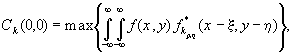 (4)
(4)
где
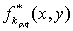 - k-я
КГС с центром разложения в точке (p,q).
- k-я
КГС с центром разложения в точке (p,q).
В работе [9] предложен иттеративный алгоритм поиска ЦС,
обладающий быстрой сходимостью. Оптический фильтр может
быть получен как с использованием фурье-преобразования КГС
изображения, так и с использованием выражения (2) для фурье-спектра
изображения. Разложение по круговым составляющим спектра
изображения производится относительно
точки
w x =0, w y =0; где w
y , w x - пространственные частоты.
При этом изображение должно быть расположено так, чтобы
его ЦС находился в центре координат входной плоскости, для
выполнения условия (4).
3.
БЧФФ круговых гармонических составляющих.
БЧФФ H(w ) функции f(x) получают при бинаризации действительной
функции [4]
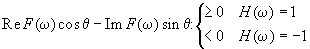 (5)
(5)
где
F(w ) - фурье-образ f(x), а угол q является пороговым
значением фазы, при переходе которой пропускание БЧФФ меняет
знак. Левая часть выражения (5) является Фурье-образом функции
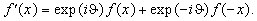 (6)
(6)
Как следует из последнего выражения для q =0, фурье-преобразование
функции f¢ (x) переходит в действительное косинусное
преобразование f(x), а при q =p /2 соответственно
в синусное. Из соотношений (5),(6) следует, что импульсный
отклик БЧФФ содержит два центросимметричных импульсных отклика
ЧФФ входного изображения в виде двух развернутых контурных
изображений. Положение каждой из симметричных копий определяется
положением изображения при синтезе фильтра, а фаза выбором
угла q в процессе бинаризации. Появление второй (развернутой
на 180o ) копии дает в выходной плоскости дополнительно
к функции корреляции функцию свертки.
Для БЧФФ, полученных при косинусном преобразовании КГС,
инвариантных к взаимной ориентации входного изображения
и эталона, сверточная составляющая имеет такую же амплитуду,
как корреляционная, но является комплексно-сопряженной по
отношению к ней. Выражение (3) в этом случае переходит в
:
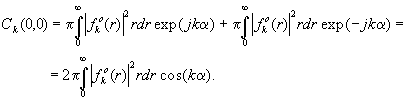 (7)
(7)
При использовании синусного преобразования КГСб косинусный
множитель в (7) переходит в синусный. Таким образом,
БЧФФ
КГС не являются инвариантными к ориентации входного изображения.
Инвариантность к ориентации может быть сохранена, если слагаемые
в выражении (7) пространственно разделены. Регистрируемая
интенсивность в этом случае не зависит от угла a , однако
каждый корреляционный максимум будет в 4 раза меньше исходного.
Пространственное разделение двух составляющих может быть
получено, если до бинаризации Фурье-спектра КГС в него внести
пространственную несущую [11] .
Если КГС рассчитываются по формулам (1)и(2), для внесения
несущей можно использовать теорему о смещении [12 ], т.е.
вычислить КГС по изображению, сдвинуть ее относительно ЦС
и выполнить преобразование Фурье и бинаризацию. Если КГС
рассчитываются по спектру изображения, то использовать теорему
о смещении нельзя, и несущая может быть внесена только в
частотной плоскости. Объясняется это тем, что при синтезе
фильтра изображение должно находиться в определенном месте
входной плоскости, сдвиг относительно которого приводит
к нарушению условия (4).
4.
Результаты эксперимента и численного моделирования.
Экспериментальная схема оптического коррелятора представлена
на Рис.1 [13] . Исходное изображение отображается на жидкокристаллический
(ЖК) модулятор света LCSIM1 с помощью телевизионной камеры
VDC1 и малогабаритного кинескопа СRT1 с диаметром экрана
20мм. Увеличенное изображение фурье-образа исходного изображения
строится в плоскости второго модулятора LCSLM2 фурье-объективом
FTL1 и микрообъективом mL. Изображение корреляционной плоскости,
полученное после обратного преобразования Фурье объективом
FTL2 и микрообъективом mL, вводится в компьютер с использованием
телекамеры VDC2 и интерфейса ввода телевизионных изображений.
Время вычисления двухмерной корреляционной функции, с учетом
времени вывода фильтра и ввода в компьютер, составляет 120
ms.
Для
расчета БЧФФ КГС использовалось изображение буквы "K" размером
64x32 элемента. Фильтры рассчитывались как по изображению,
так и по его спектру. Алгоритмы расчета представлены на
Рис.2. Фильтры КГС, полученные для изображений (Рис.2а),
дают более высокий и устойчивый корреляционный максимум
при численном моделировании по сравнению с фильтрами, рассчитанными
по спектру (Рис.2б). Это вызвано более высоким уровнем ошибки,
обусловленной дискретным представ-
лением
фурье-спектра по сравнению с изображением. Кроме того, расчет
КГС по спектру требует большего объема вычислений, т.к.
производится разложение комплексной функции.
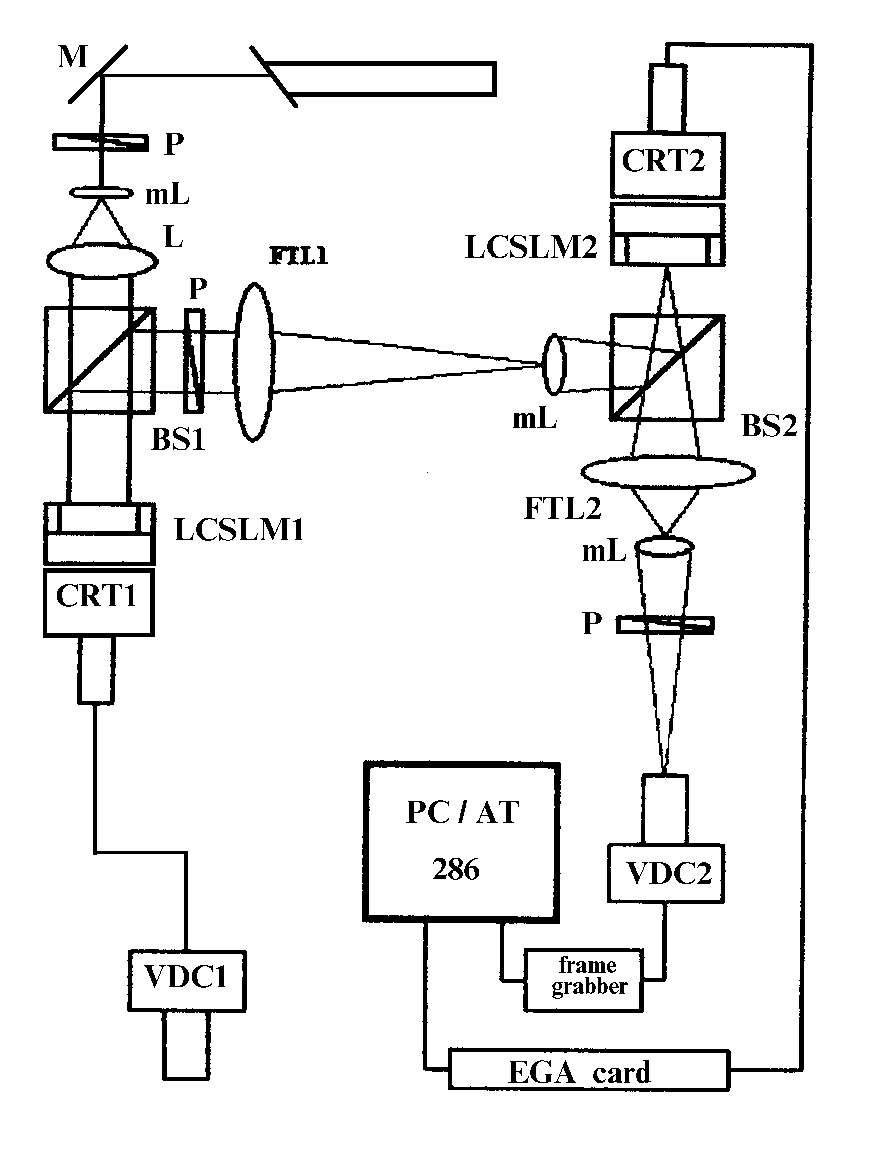
Рис.1.
Экспериментальная схема оптического коррелятора.
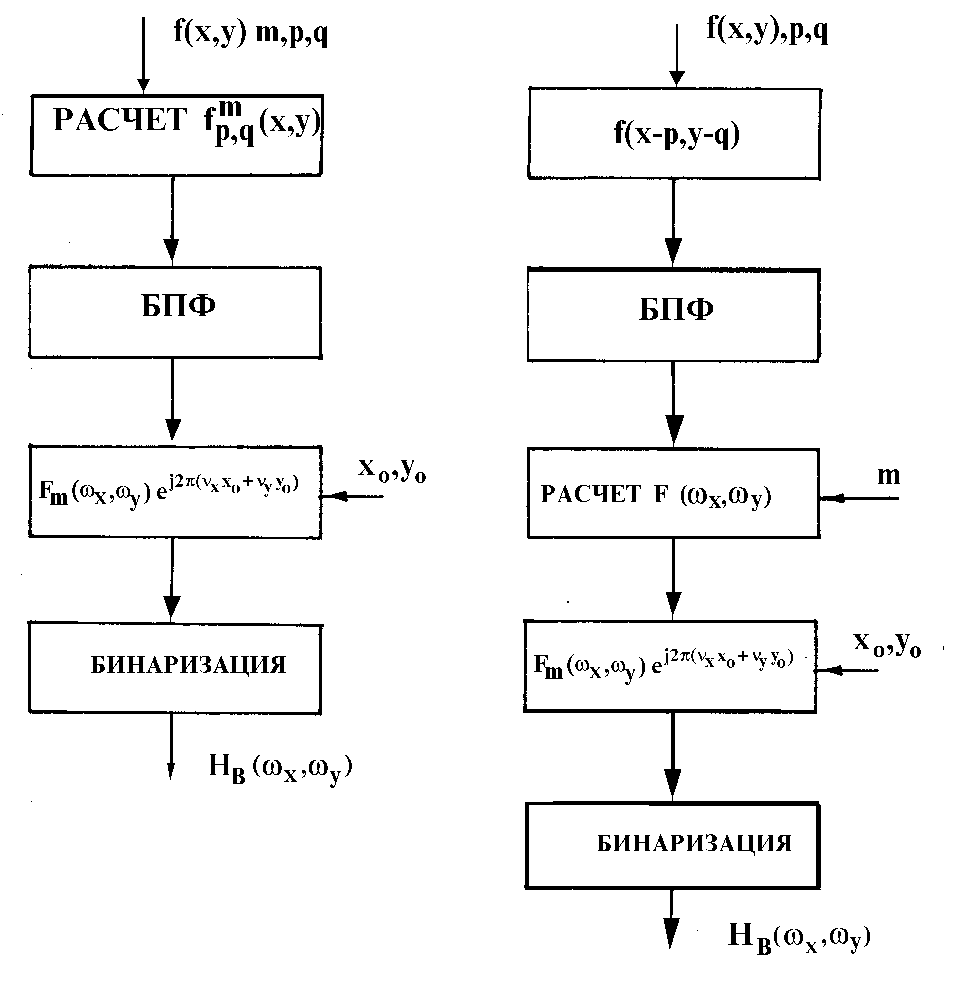
а) б)
Рис.2.
Два алгоритма расчета БЧФФ КГС с несущей по изображению
(а) и по его фурье-спектру (б).


Рис.3.
Относительное распределение интенсивности света в корреляционной
плоскости, полученное в экспериментальной схеме (б,г) и
при численном расчете (а,в) для БЧФФ 0-й КГС без несущей
при углах поворота входного изображения относительно эталона
на 0o (а,б) и 90o (в,г).
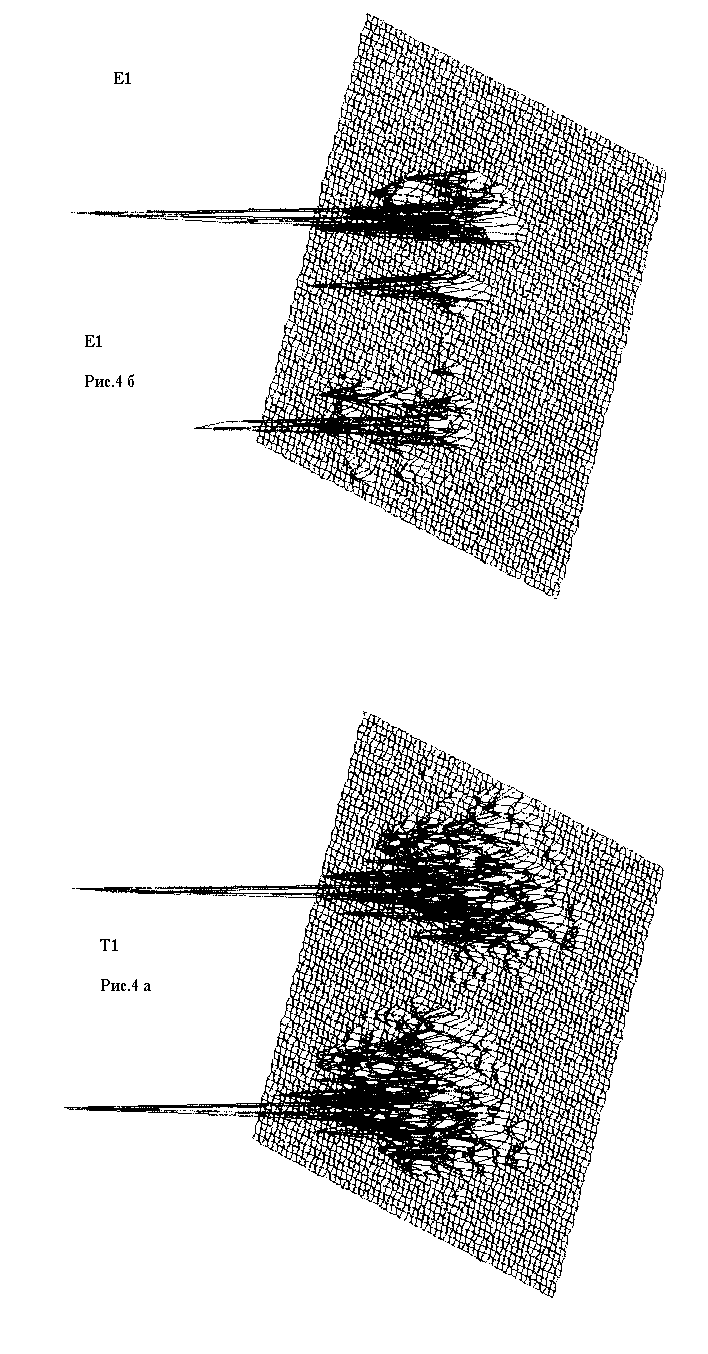
 Рис.4.
Относительное распределение интенсивности света в корреляционной
плоскости, полученное в экспериментальной схеме (б,г) и
при численном расчете (а,в) для БЧФФ 0-й КГС с несущей при
углах поворота входного изображения относительно эталона
на 0o (а,б) и 90o (в,г).
Рис.4.
Относительное распределение интенсивности света в корреляционной
плоскости, полученное в экспериментальной схеме (б,г) и
при численном расчете (а,в) для БЧФФ 0-й КГС с несущей при
углах поворота входного изображения относительно эталона
на 0o (а,б) и 90o (в,г).
БЧФФ
размером 128x64 элементов различных порядков КГС, полученные
при косинусном преобразовании, последовательно выводились
на экран CRT2 в виде массивов черно-белых прямоугольников,
соответствующих бинарному распределению фазового фильтра.
Переход к фазовой модуляции осуществлялся на основе гибридного
ориентационного эффекта в слое ЖК.
Изображение корреляционной плоскости, полученное в экспериментальной
схеме и при численном расчете для БЧФФ 0-й КГС без несущей
при углах поворота входного изображения относительно эталона
на 0o 90o , показано на Рис.3. Выходная
плоскость содержит единственный пик характерной формы, величина
которого не меняется при повороте входного изображения только
для 0-й КГС. Для БЧФФ КГС с несущей (Рис.4) в выходной плоскости
появляются два пика согласно выражению (7), однако их величина
остается постоянной при повороте изображения для КГС любого
порядка. Несмотря на то, что интенсивность пиков уменьшается
в 4 раза, они сохраняют свою характерную форму.
На Рис.5 приведены экспериментальные и теоретические зависимости
значений корреляционных максимумов от угла поворота входного
изображения для БЧФФ КГС 0, 4 и 12 порядков без несущей.
Ошибка поворота дискретного массива обуславливает 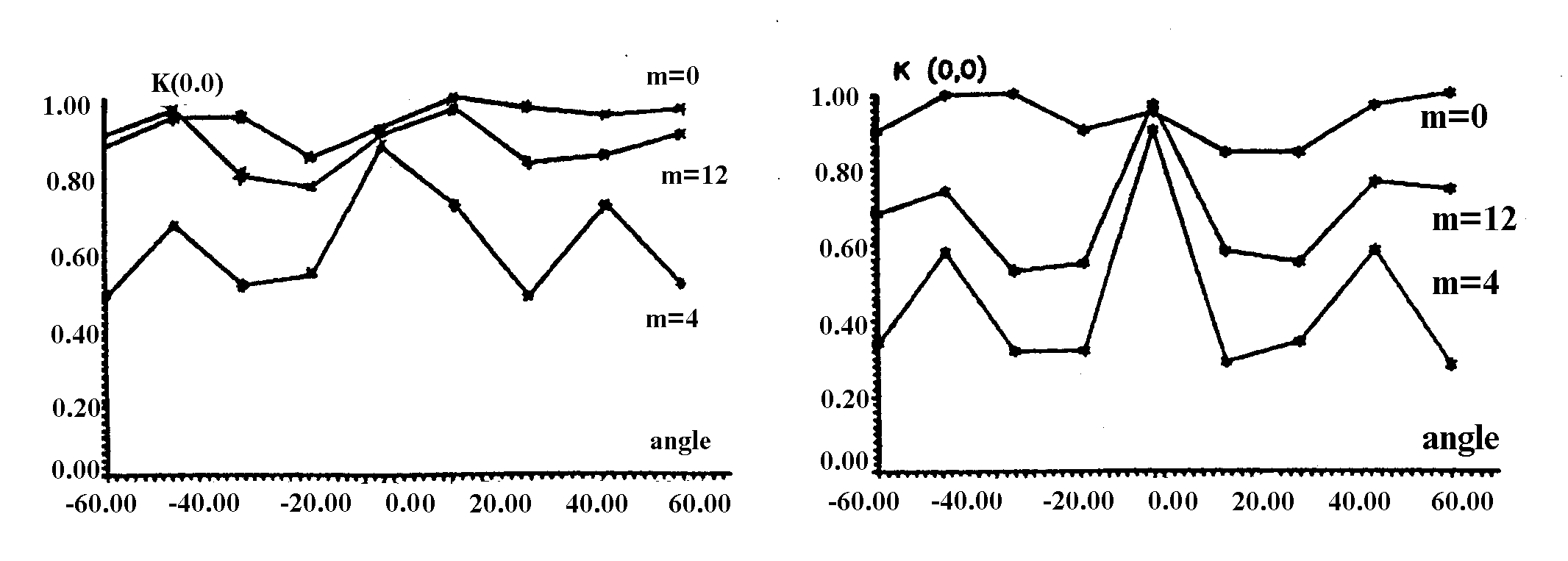
Рис.5.
Экспериментальные (а) и теоретические (б) зависимости нормированных
значений корреляционных максимумов от угла поворота входого
изображения для БЧФФ КГС 0, 4 и 12 порядков без несущей.
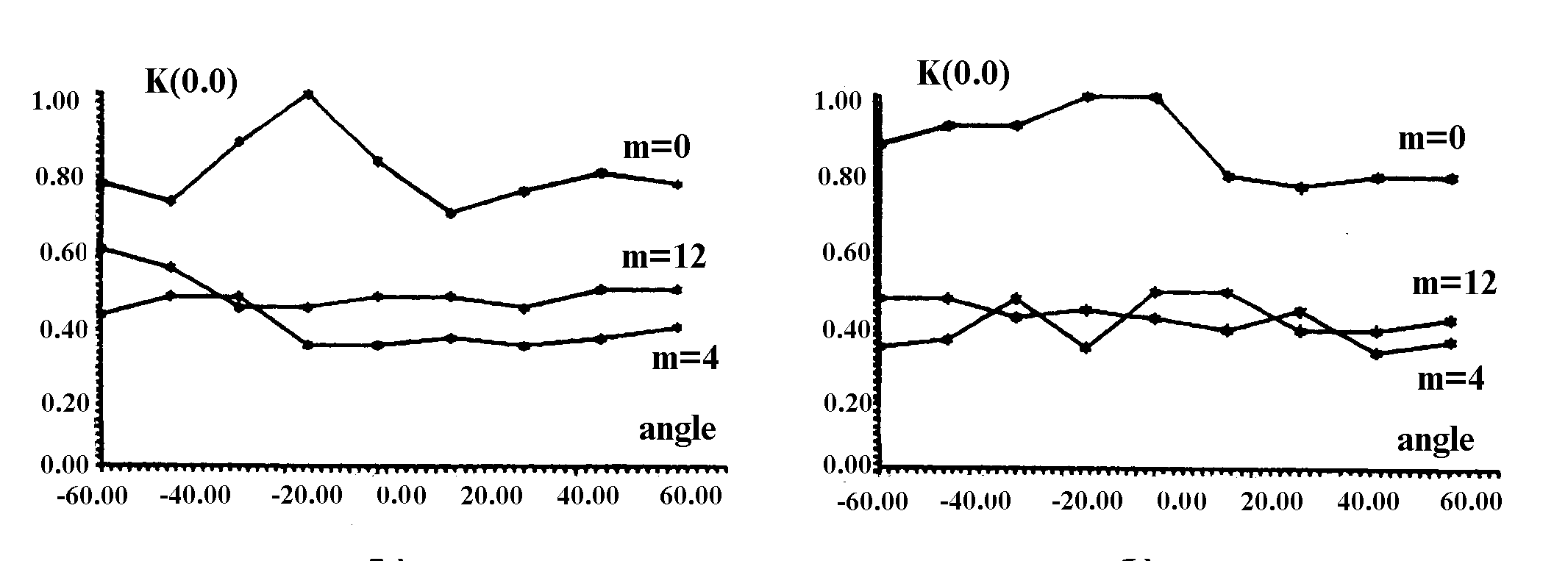
Рис.6
Экспериментальные (а) и теоретические (б) зависимости нормированных
значений корреляционных максимумов от угла поворота входного
изображения для БЧФФ КГС 0, 4 и 12 порядков с несущей.
более
низкую величину расчетных значений для КГС высоких порядков.
При выбранных углах поворота входного изображения значения
корреляционных максимумов для БЧФФ КГС 0-го и 12-го порядков
сохраняют свои величины, а максимумы БЧФФ КГС 4-го порядка
периодически меняются через 45o . Как видно из
Рис.6, величина корреляционных максимумов БЧФФ КГС любого
порядка с несущей остается постоянной.
5.
Заключение.
Полученные экспериментальные и теоретические результаты
использования в оптических корреляторах БЧФФ КГС с несущей
демонстрируют эффективность их применения как фильтров,
инвариантных к ориентации входных изображений и сохраняющих
достоинства БЧФФ. При расчете фильтров разложение по круговым
гармоническим составляющим может производиться как по изображению,
так и по его спектру. В последнем случае центр соответствия
, относительно которого производится разложение, должен
быть совмещен с центром входной плоскости до выполнения
фурье-преобразования. Кроме того, при расчете фильтров по
спектрам несущая не может вводиться сдвигом изображения
во входной плоскости, поскольку это приводит к смещению
центра разложения. Взаимное расположение двух корреляционных
пиков для БЧФФ КГС с несущей может быть выбрано подбором
частоты несущей так, чтобы расстояние между ними было меньше
размеров изображения. В этом случае не будет возникать ошибки
при опознавании изображений, присутствующих в сложных сценах.
Положение корреляционных максимумов, как и в случае согласованных
фильтров, однозначно связано с положением
изображений
во входной плоскости, что позволяет определять координаты
изображений.
Литература.
1.
Vander Lugt A. IEEE Trans. Inf. Theory, vol.IT-10, }2, 1964,
pp.139-145.
2.
Г.И.Василенко, Л.М.Цибулькин. Голографические распознающие
устройства.- М., Радио и связь, 1985.
3.
J.L.Horner, P.D.Gianino. Appl.Opt., v.23, №6, 1984, pp.812-816.
4.
D. L. Flannery and J. L. Horner, Proc. IEEE, Vol. 77, pp.
1511-1527, 1989.
5.
T. H. Barnes, T. Eiju, K. Matsuda, and N. Ooyama, Appl.
Opt. vol. 28, pp.4845-4852, 1989.
6.
D. L. Flannery, A. Biernacki, J. Loomis, and S. Cartwright,
Appl. Opt., vol.25, pp.2484-2490, 1986.
7.
V.V.Dadeshidze, I.N.Kompanets, and A.A.Vasiliev, Int. Top.
Meet. on Optical Computing, Minsk, 1992, 29E32.
8.
J. Florence and R. Gale, Appl. Opt., Vol. 27, pp. 2091-2093,
1988.
9.
Y.H.Hsu, H.H.Arsenault, C.April. Appl.Opt., vol.21, №22,
1982, pp.4012-4019.
10.
J.Rosen, J.Shamir. Appl.Opt., vol.27, №14, 1988, pp.2895-2899.
11.
L.Leclerc, Y.Sheng, and H.Arsenault. Appl.Opt., vol.30,
№32, pp. 4643-4649.
12.
А.Папулис. Теория систем и преобразований в оптике. - М.,
Мир, 1971.
13.
А.А.Васильев, В.В.Дадешидзе, И.Л.Линдунен, И.Н.Компанец
- готовится к печати.

