КОРРЕЛЯЦИОННЫЕ ЭФФЕКТЫ ПРИ ОСВЕЩЕНИИ
РАССЕИВАЮЩИХ СРЕД ЛАЗЕРНЫМ ПУЧКОМ С

ИНТЕРФЕРЕНЦИОННОЙ СТРУКТУРОЙ

В.П.Рябухо, Ю.А.Аветисян, Л.И.Голубенцева, Д.А.Зимняков

Саратовский Университет, 410701,Саратов, Астраханская, 81

Институт Машиноведения РАН, 410740, Саратов, Рабочая, 24

В лекциях на Школах и статьях Георгий Викторович Скроцкий неоднократно обращался к вопросам проявления корреляционных свойств спекл-полей при интерферометрии. В [1,2] показана возможность проявления корреляционных свойств диффузно-когерентного излучения в поле дифракции за голограммой- интерферометром сдвига. В этих работах рассматривались d -коррелированные рассеиватели, для которых, как и установлено в [1,2], корреляционные свойства спекл-полей определяются аналогом теоремы Ван-Циттера-Цернике, сформулированной для излучения тепловых источников [3,5]. Для слабых рассеивателей с плавными оптическими неоднородностями и ближнего поля дифракции уже нельзя пользоваться вышеназванной теоремой. В настоящей работе рассматриваются проявления корреляционных свойств спекл-полей при освещении слабых фазовых рассеивателей пучком с регулярной интерференционной структурой. В этом случае за рассеивателем, также как и в [1,2] за голограммой, формируются два взаимно смещенных спекл модулированных поля. Сдвиг полей линейно увеличивается с удалением от рассеивателя, что сопровождается уменьшением контраста полос средней интенсивности в рассеянном поле [6]. Эволюция контраста полос зависит от корреляционных свойств рассеянного поля, которые определяются статическими характеристиками неоднородностей рассеивателя, а также дифракционными эффектами, обусловленными ограниченностью в поперечном сечении освещающего лазерного пучка.

Лазерные пучки с интерференционными полосами - пространственно-модулированные пучки, используются в голографической и спекл-интерферометрии для измерения микроперемещений [7,8], а в лазерной анемометрии [9] для счета и измерения скорости движения частиц. В этих методах интерференционные полосы имеют малый пространственный период, сравнимый с размерами неоднородностей. В настоящей работе рассматри-

ваются пучки с периодом полос, значительно превышающим поперечные размеры неоднородностей.

Из практических соображений целесообразно использовать освещающий лазерный пучок с параллельными полосами, которые формируются при интерференции двух идентичных волн, распространяющихся под малым углом q друг к другу. Комплексную амплитуду такого пучка в плоскости 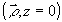можно записать в виде:

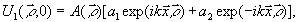(1)

где a₁, a₂ - константы, 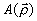- комплексная амплитуда волн, 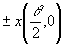- составляющие единичных векторов направлений распространения волн на плоскость 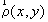. В поперечном сечении пучка формируются прямолинейные полосы, параллельные оси x с периодом L =l / q и контрастом V₀=2a₁a₂/(a₁²+a₂²). Если неоднородности рассеивателя плавные, т.е. их радиус корреляции l_ф значительно превышает длину волны l и среднее квадратичное отклонение приобретаемой разности хода 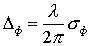(l_ф>>l и l_ф>> D _ф), где s _ф² - дисперсия фазовых флуктуаций поля, то такой рассеиватель удовлетворяет модели случайного фазового экрана (СФЭ) [4,5] с функцией пропускания вида

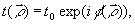(2)

где 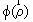- случайный фазовый набег. Для малых углов падения q освещающего пучка функция пропускания остается неизменной, поэтому граничное поле в плоскости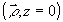, располагающейся в непосредственной близости за СФЭ, можно представить в виде

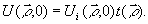(3)

Используя приближение дифракции Френеля можно показать, что в параксиальной области рассеянное поле представляет собой суперпозицию двух взаимно смещенных спекл-полей с комплексными амплитудами вида

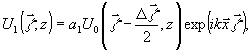(4)

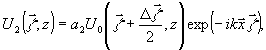(5)

где 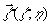- координата плоскости наблюдения:

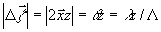- взаимный сдвиг полей; 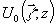- рассеянное поле при освещении поверхности по нормали (x=0) одним из пучков:

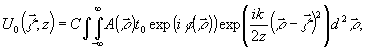(6)

где

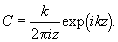
Будем полагать, что средние интенсивности каждого из интерферирующих полей медленно меняются в плоскости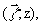поэтому 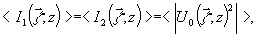где угловые скобки означают осреднение по ансамблю реализаций спекл-полей. Осреднение интенсивности рассеянного поля необходимо для сглаживания спекл-модуляции и выделения детерминированной составляющей в пространственном распределении интенсивности. Это распределение имеет вид:

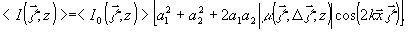(7)

где

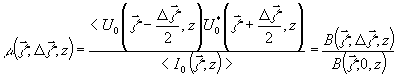(8)

• коэффициент поперечной корреляции комплексной амплитуды рассеянного поля при освещении СФЭ по нормали одним пучком с комплексной амплитудой

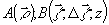
- поперечная кор-

реляционная функция. Из (7) следует, что в рассеянном поле наблюдаются интерференционные полосы средней интенсивности с периодом L = l / q и контрастом

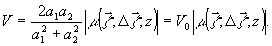(9)

Из-за взаимного сдвига полей D z контраст полос уменьшается с удалением от экрана. Для СФЭ с различными параметрами s _ф² и l_ф, контраст изменяется по-разному. При этом зависимость m от z проявляется одновременно за счет взаимного сдвига спекл-полей и трансформации рассеянного поля вдоль продольной координаты z , что в значительной мере проявляется при ограниченном освещающем пучке.

Используя (6), для поперечной корреляционной функции 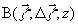получим [4,5] выражение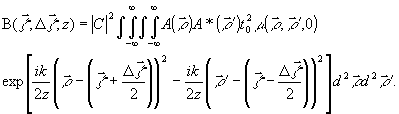(10)

где 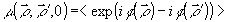- коэффициент корреляции пропускания СФЭ (2). Если 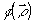- статически однородный гауссов процесс с нулевым средним, то 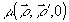принимает вид [4,5]

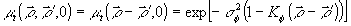(11)

где 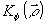- коэффициент корреляции фазы граничного поля. Используя замену переменных: 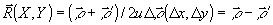, уравнение (10) можно привести к более удобному для анализа виду: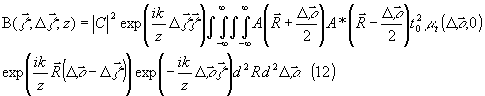

Далее выделим два важных случая освещения СФЭ безгранично широким или ограниченным лазерным пучком.

Если освещающий пучок достаточно широк и коллимирован 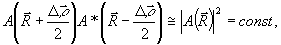то интегрирование по 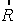в (12) дает d -функцию и для 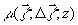получим выражение, что и для коэффициента корреляции граничного поля

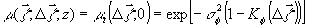(13)

Имеем важный результат - корреляционные свойства рассеянного поля сохраняются за СФЭ [4], несмотря на развивающуюся в этом поле спекл-модуляцию. Используя спектральные представления, этот результат можно объяснить следующим образом. Для безграничного параллельного освещающего пучка и статически однородного СФЭ пространственный спектр мощности рассеянного поля не изменяется в продольном направлении, поскольку модуль спектральной передаточной функции свободного пространства в этом случае равен единице [10]. Такой же вывод можно сделать и из чисто эвристических соображений, принимая во внимание отсутствие влияния апертурных ограничений на угловой спектр рассеянного поля. Поэтому корреляционная функция поля, определяемая в соответствии с теоремой Винера-Хинчина через Фурье-образ пространственного спектра мощности, также будет неизменной в продольном направлении [4]. При ограниченном освещающем пучке вблизи СФЭ имеется область, в которой коэффициент корреляции поля остается неизменным. Протяженность этой области z_o зависит от ширины освещающего пучка 2w и параметров СФЭ s _ф² и l_ф и оценивается соотношением z_o » p w l_ф/l s _ф [4]. Поэтому при соответствующем выборе ширины освещающего пучка 2w для описания эволюции контраста полос V в ближней области дифракции можно использовать уравнение (13).

В качестве ограниченного освещающего пучка нами рассматривался коллимированный гауссов пучок - 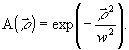В этом случае интеграл (12) допускает аналитическое интегрирование по переменной R и принимает вид:

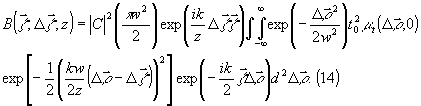
Последующие расчеты для простоты выполнены для одномерного СФЭ, полагая радиус корреляции фазы вдоль оси y равным бесконечности, l_фy>>w. В этом случае в (14) интегрирование по D y проводилось аналитически, а по D x - численно в приосевом приближении, 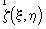=0. Коэффициент корреляции фазы граничного поля К_ф(D x) аппроксимировался функцией вида:

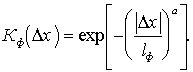(15) На рис.1 представлены результаты численных расчетов коэффициента |m (z)| для безграничного и ограниченных освещающих

пучков при гауссовом (a=2) коэффициенте корреляции фазы К_ф для следующих параметров: l =0.63 мкм; L =0.75 мм; s _ф=1.5; l_ф=20 мкм. Влияние ограниченности освещающего пучка начинает проявляться заметным образом лишь при достаточно малом радиусе пучка w , малом l_ф и, что важно отметить, малой s _ф². При z>z_o появляется локальный минимум и последующий максимум, а затем асимптотическое стремление к нулю в дальней области дифракции (кривая 6 на рис.1 с отсчетом z по верхней шкале). Увеличение контраста полос можно объяснить фильтрующими свойствами свободного пространства [10], которые обеспечивают выделение нерассеянной компоненты на фоне рассеянной состав-

ляющей поля. Полосы при этом наблюдаются только в пределах нерассеянного пучка.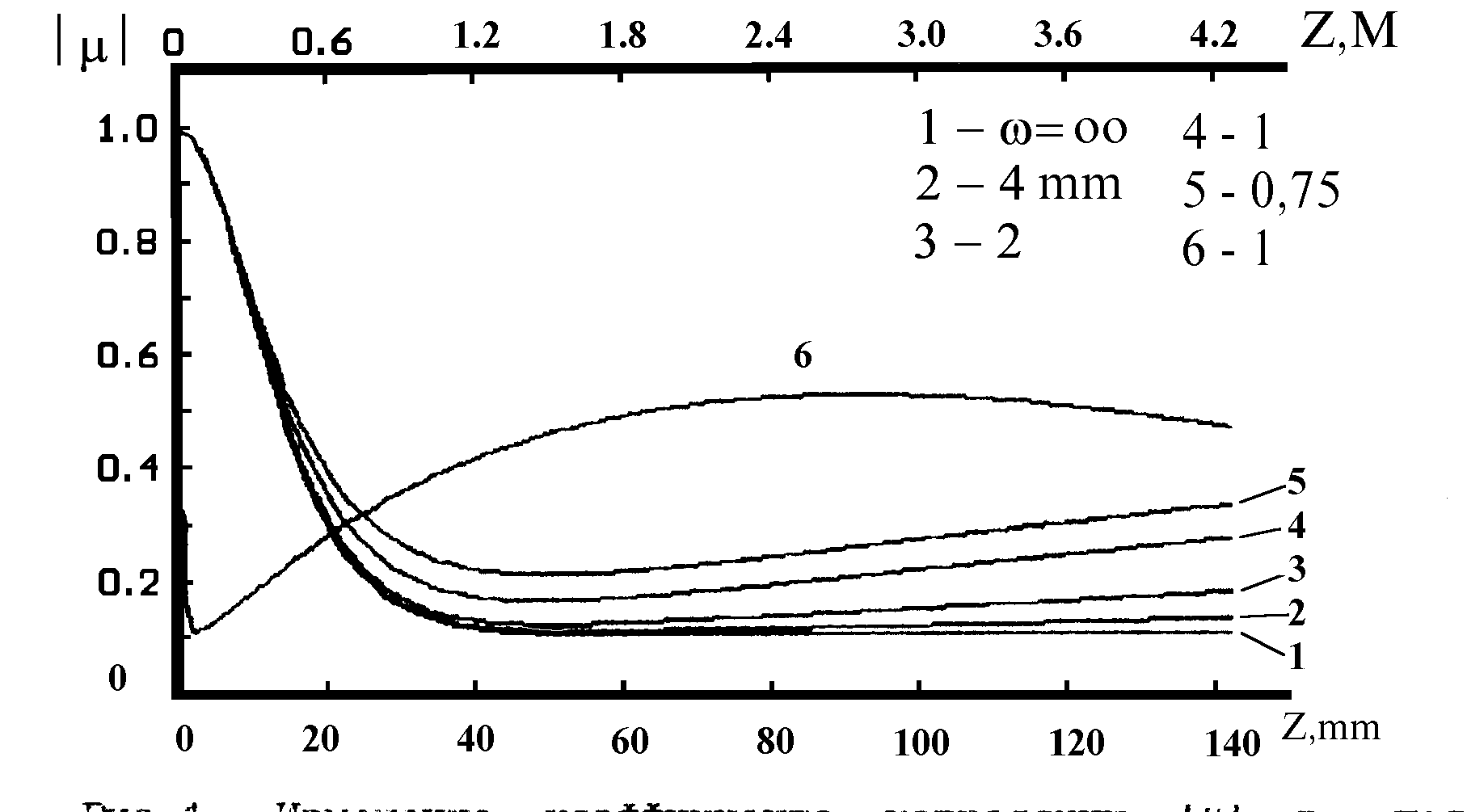

Рис.1. Изменение коэффициента корреляции | m | в поле

дифракции ограниченного пучка на СФЭ.

В эксперименте с целью осреднения спекл-модуляции и получения фотоэлектрического сигнала, пропорционального средней интенсивности излучения, использовался фотоприемник со щелевой апертурой. Для статически однородного поля такое осреднение эквивалентно осреднению по ансамблю реализаций спекл-полей, введенному в (7) и (8).

С технической точки зрения в измерениях удобнее использовать в освещающем пучке подвижные интерференционные полосы [6]. В этом случае при неподвижном приемнике формируется переменный фотоэлектрический сигнал, коэффициент модуляции b которого пропорционален контрасту V средней интенсивности регистрируемого поля, b =MV. Коэффициент пропорциональности M определяется сглаживающим действием апертуры фотоприемника. Измеряя коэффициент модуляции фотоэлектрического сигнала b _о от освещающего пучка (без образца), который равен b _о=MV_о, где V_o - контраст полос в этом пучке, можно найти отношение V/V_o=b /b _о. Следовательно, в соответствии с (9),

искомое значение модуля коэффициента корреляции поля экспериментально определяется простым выражением |m | = b /b _о.

В качестве СФЭ использовались фазовые (отбеленные) спеклограммы, модулирующие пучок по фазе за счет плавных пространственных флуктуаций толщины и показателя преломления эмульсионного слоя. Изменяя экспозицию и размер регистрируемых спеклов, можно в достаточно широких пределах изменять статические параметры таких СФЭ - s _ф² и l_ф. Более того, используя нелинейность фотоотклика или сложную апертуру рассеивателя при записи спеклограммы, можно получать СФЭ с многомасштабным или сильно осциллирующим коэффициентом корреляции фазы граничного поля К_ф.

На рис.2 приведены экспериментальные данные и теоретические

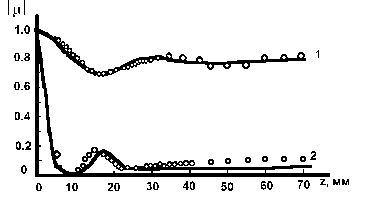
Рис.2. Экспериментальные точки и теоретические графики

зависимости модуля коэффициента корреляции рассеян-

ного поля для СФЭ (спеклограмм) с различными параметрами неоднородностей: 1-s _ф=0.615, l_ф=6.4 мкм, а=2,45;

2 - s _ф=1.12, l_ф=7.8 мкм, а=2; 3 - s _ф=1.3, l_ф=5.6 мкм, а=2,5.

зависимости |m (z)|. Численные расчеты выполнены для ограниченного освещающего пучка (w = 4 мм) и параметров СФЭ, полученных по экспериментальным данным в приближении безграничного освещающего пучка, т.е. при использовании уравнения (13) и (15).

Дисперсия s _ф², как и в [11], определялась по минимальному уровню экспериментальных значений m _о=exp(-s _ф²); радиус корреляции l_ф - с помощью уравнения 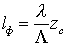, где z_о соответствует уровню m _c , для которого коэффициент К_ф уменьшился в е-раз .Показатель степени а для К_ф также легко определить из (15) по экспериментальным данным m и z, решая относительно а уравнение

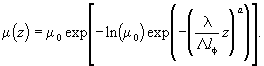(16)

Вышеописанные эффекты позволяют в определенной мере судить о характере эволюции корреляционных свойств спекл-полей за рассеивателем. В ближней области дифракции коэффициент поперечной корреляции поля, как отмечалось в [11], остается неизменным, равным коэффициенту корреляции граничного поля, несмотря на развивающуюся спекл-модуляцию, которая для

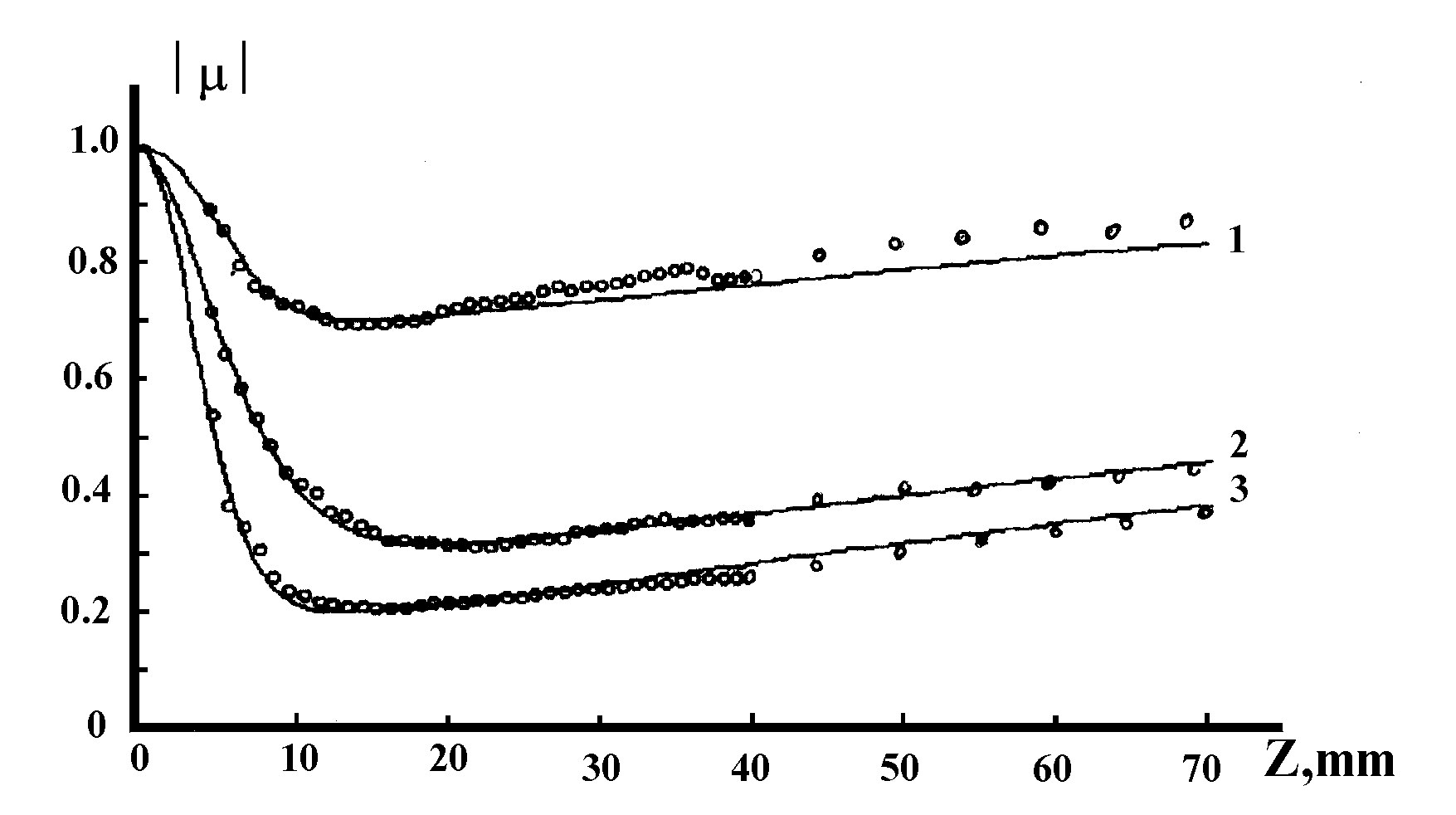
Рис.3. Изменение коэффициента корреляции рассеянного поля

при осциллирующем коэффициенте корреляции фазы:

1 - s _ф=0.62, l_ф=28 мкм, l_ф1=6.4 мкм, а=2.5;

2 - s _ф=2.2 , l_ф=21 мкм, l_ф1= 8 мкм, а=2,3.

 

рассеивателей с s _ф²>1 уже в рассматриваемой области становится развитой.

Апертурные ограничения освещающего пучка приводят к трансформации корреляционных свойств поля для z>z_o=wl_{ф/ l s ф} , что сопровождается увеличением контраста наблюдаемых интерференционных полос. Оценки показывают, что максимум контраста приходится на дальнюю область дифракции Френеля, когда в апертуреосвещающего пучка укладываются несколько зон Френеля.Дальнейшее уменьшение контраста полос (рис.1, кривая 6) соответствует области, в которой корреляционные свойства описываются теоремой Ван-Циттерта-Цернике. При этот следует иметь ввиду, что рассматриваются корреляционные свойства комплексной амплитуды поля в целом, а не отдельно его флуктуационной части, получаемой за вычетом среднего значения, отвечающего нерассеянной компоненте поля. Поэтому для собственно рассеянного поля результаты будут другими.

Авторы благодарны А.Е.Гриневичу и В.Л.Хомутову за помощь в экспериментах и профессору В.В.Тучину за плодотворные обсуждения результатов работы.

ЛИТЕРАТУРА

1. Власов Н.Г., Скроцкий Г.В., Соловьев Е.Г. В сб.: Проблемы голографии. Вып.1.- М.: МИРЭА, 1973, с.85-88.

2. Власов Н.Г., Скроцкий Г.В., Соловьев Е.Г. // Кв.электр., 1972, №3, с.84-86.

3. Борн М., Вольф Э. Основы оптики.- М.: Наука, 1970. 855 с.

4. Рытов С.М., Кравцов Ю.А., Татарский Б.И. Введение в статистическую радиофизику. Ч.11.- М.: Наука, 1978.- 463 с.

5. Гудмен Дж. Статистическая оптика.- М.: Мир, 1988.- 528 с.

6. Рябухо В.П., Зимняков Д.А., Голубенцева Л.И., Фелулеев Б.В., Полькина О.И. // В сб.: Оптические поля и оптические методы обработки информации.- М.: МФТИ, 1991.- с.29-37.

7. Джоунс Р., Уакс К. Голографическая и спекл-интерферометрия.- М.: Мир, 1986.- 328 с.

8. Локшин Г.Р., Козел С.М., Клименко И.С., Белонучкин В.Е. // Опт. и спектр., 1992, т.72, №6, с.1444-1450.

9. Б.С.Ринкевичус. Лазерная диагностика потоков. М.: МЭИ, 1990.- 288 с.

10. Гудмен Дж. Введение в Фурье-оптику.- М.: Мир, 1970.- 364 с.

11. Ангельский О.В. // Кв. электр., 1992, т.19, №12, с. 1151-1158.