МЕТОДЫ
ИССЛЕДОВАНИЯ СОСТОЯНИЙ
КОГЕРЕНТНЫХ
ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ
А.Е.
Краснов
Физический
институт им. П.Н. Лебедева РАН
117924,
Москва, Ленинский пр., 53
Введение.
Понятие физически-оптимального синтеза детекторов электромагнитного
поля.
Когерентное
электромагнитное поле в общем случае является квази-классическим
физическим объектом и при его наблюдении необходимо использовать
статистический аппарат оператора (матрицы) плотности [1,2].
В соответствии с данным аппаратом любое устройство, измеряющее
какую-либо связанную с полем физическую величину L, производит
усреднение по всевозможным начальным условиям состояния
поля (описываемым оператором плотности  )
оператора
)
оператора 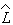 ,
отвечающего данной физической величине. В результате формируется
среднее значение физической величины: <L> = Tr {
,
отвечающего данной физической величине. В результате формируется
среднее значение физической величины: <L> = Tr {
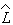 },
при условии Tr {
},
при условии Tr { }
= 1, где Tr означает след оператора.
}
= 1, где Tr означает след оператора.
Обычно
в физических задачах известен вид операторов  и
и 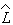 , а
также зависимость
, а
также зависимость 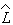 от динамических переменных поля. Совершенно другая ситуация
имеет место в задачах обнаружения сигналов на фоне шумов,
их выделения, оценки параметров и распознавания. В этом
случае известен (теоретически) лишь вид оператора плотности
поля, а оператор физической величины необходимо найти. Процедуру
нахождения такого оператора физической величины (или нескольких
физических величин) будем называть в дальнейшем физическим
синтезом измерителей или детекторов поля.
от динамических переменных поля. Совершенно другая ситуация
имеет место в задачах обнаружения сигналов на фоне шумов,
их выделения, оценки параметров и распознавания. В этом
случае известен (теоретически) лишь вид оператора плотности
поля, а оператор физической величины необходимо найти. Процедуру
нахождения такого оператора физической величины (или нескольких
физических величин) будем называть в дальнейшем физическим
синтезом измерителей или детекторов поля.
В
данном случае понятие физического синтеза противопоставляется
понятию технического синтеза, нашедшего широкое применение
в фильтрации сигналов после оcновополагающих работ А.Колмогорова,
Н.Винера, В.Котельникова, Д.Мидлтона, Р.Стратоновича, Р.Калмана
и Р.Бьюси, Л. Вайнштейна и
В.Зубакова,
В.Тихонова и Н.Кульмана, В. Репина и Г. Тартаковского [3-11].
В этих и более современных работах [12,13] основное внимание
уделено проблемам технически-оптимального синтеза,
при котором вид оператора физической величины считается
известным. Тогда, обычно с точностью до вектора c =
(c1, c2, ... cN) неизвестных коэффициентов, формируется
некоторое преобразование Á [<L>, с] наблюдаемой
физической величины <L> (фильтр наблюдаемых данных),
оптимизирующее некий функциональный критерий F (c)
качества фильтрации [6,10,11]. Так, например, при винеровской
фильтрации в качестве критерия F (c) выбирается
среднеквадратичное отклонение F (c) = <|
Á [<L>,с] - Á  |
|
 >
выхода синтезируемого фильтра Á [<L>,с]
от некоторого известного значения Á
>
выхода синтезируемого фильтра Á [<L>,с]
от некоторого известного значения Á  [4,5,6].
Неизвестные коэффициенты находятся при оптимизации (минимизации)
значения функционала F (c).
[4,5,6].
Неизвестные коэффициенты находятся при оптимизации (минимизации)
значения функционала F (c).
Физичеки-оптиальный
синтез отличается от технически-оптимального синтеза тем,
что заранее неизвестен вид оператора, отвечающего процедуре
измерения физических величин, связанных с полем. Тем самым
неизвестна и сама процедура. Она должна быть найдена из
условий, включающих: статистику поля ( ),
критерий оптимальности (F ) детектирования поля и некоторые
граничные условия наблюдения поля. После этого должен быть
использован технически-оптимальный синтез, но уже применительно
к известной измеряемой физической величине.
),
критерий оптимальности (F ) детектирования поля и некоторые
граничные условия наблюдения поля. После этого должен быть
использован технически-оптимальный синтез, но уже применительно
к известной измеряемой физической величине.
Для
задач, связанных с построением детекторов электромагнитного
поля, А.Холево и К Хелстромом был предложен подход к физически-оптимальному
различению состояний квантовых полей на основе синтеза измеряющих
(детектирующих) операторов [14,15]. Однако, основное внимание
было уделено математическому формализму описания состояний
поля (через ненаблюдаемый оператор плотности), далекому
от экспериментальной реализации.
Ниже,
при решении задачи физически-оптимального синтеза, мы будем
придерживаться результатов работ [14,15], однако выберем
более приемлемый для экспериментальной реализации путь,
основанный на наблюдаемых оценках состояний когерентных
электромагнитных полей. При этом для конкретизации условий
наблюдения поля будем в дальнейшем интересоваться только
такими его состояниями, которые связаны с разнообразием
форм как временных, так и пространственных огибающих поля,
считая,
что
поля, отличающиеся лишь несущими, идентичны по состояниям.
1.
Роль описания состояний электромагнитного поля
при
физически-оптимальном синтезе.
Выберем
критерий, отвечающий нахождению такой процедуры измерения,
которая позволяет наиболее точно находить различие между
двумя состояниями поля, описываемыми соответственно операторами

 и
и 
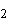 .
При измерении физической величины L в каждом состоянии поля
будут детектироваться ее значения <L
.
При измерении физической величины L в каждом состоянии поля
будут детектироваться ее значения <L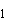 >
и <L
>
и <L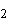 >
с соответствующими дисперсиями s
>
с соответствующими дисперсиями s 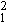 = <[L-<L
= <[L-<L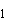 >]
>]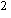 >
и s
>
и s 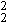 = <[L-<L
= <[L-<L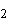 >]
>]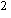 >.
При этом среднеквадратичное отклонение самих измеряемых
величин s
>.
При этом среднеквадратичное отклонение самих измеряемых
величин s 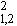 = [<L
= [<L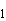 >
- <L
>
- <L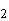 >]
>]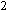 .
Тогда, в качестве искомого критерия естественно выбрать
критерий Фишера: F (L) = s
.
Тогда, в качестве искомого критерия естественно выбрать
критерий Фишера: F (L) = s 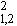 / (s
/ (s 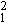 +s
+s
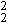 ) [16].
Максимизация данного критерия будет соответствовать наибольшей
разрешающей способности синтезируемого измерителя состояния
электромагнитного поля.
) [16].
Максимизация данного критерия будет соответствовать наибольшей
разрешающей способности синтезируемого измерителя состояния
электромагнитного поля.
Отмеченные
выше задачи обнаружения и распознавания сигналов на фоне
шумов решаются на основе введенного критерия. В таких задачах
c позиции статистической теории решений [10-12] должны рассматриваться,
как минимум, две конкурирующие гипотезы: 1) Г1 - поле находится
в состоянии шума 
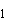 =
=

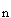 ;
2) Г2 - поле находится в смешанном состоянии сигнала и шума
;
2) Г2 - поле находится в смешанном состоянии сигнала и шума

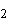 =
=

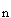 Ä
Ä 
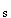 ,
где Ä - знак свертки [2]. Легко показать, что в случае
гауссовых статистик значений физической величины L с критерием
F (L) связан функционал L [Г2 /Г1] отношения правдоподобия
гипотез (L [Г2 /Г1] = exp{F (L)}), используемый
в качестве основного оптимизационного критерия при технически-оптмальном
синтезе [10].
,
где Ä - знак свертки [2]. Легко показать, что в случае
гауссовых статистик значений физической величины L с критерием
F (L) связан функционал L [Г2 /Г1] отношения правдоподобия
гипотез (L [Г2 /Г1] = exp{F (L)}), используемый
в качестве основного оптимизационного критерия при технически-оптмальном
синтезе [10].
К
сожалению решить оптимизационную задачу в общем виде не
представляется возможным ввиду того, что введенный критерий
нелинейно зависит от спектральных значений искомого оператора.
Действительно, вводя соответствующие матричные
элементы
вместо  и
и 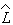 (матрицу
плотности s
(матрицу
плотности s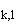 и спектр l
и спектр l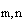 ),
средние величины в F (L) можно выразить в
),
средние величины в F (L) можно выразить в
виде
билинейной формы <L> = Tr {
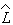 }
=
}
= 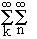 s
s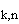 l
l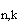 .
Матрица плотности и спектр являются вполне непрерывными
[17]. Поэтому нелинейная задача оптимизации становится бесконечномерной.
С другой стороны, под совокупностью индексов {k,n} скрываются
динамические перемен-ные поля, выбирая которые должным образом
можно упростить вид билинейной формы. Оператор
.
Матрица плотности и спектр являются вполне непрерывными
[17]. Поэтому нелинейная задача оптимизации становится бесконечномерной.
С другой стороны, под совокупностью индексов {k,n} скрываются
динамические перемен-ные поля, выбирая которые должным образом
можно упростить вид билинейной формы. Оператор  плотности поля не является наблюдаемой величиной. Получаемый
же при решении оптимизационной задачи наблюдаемый оператор
плотности поля не является наблюдаемой величиной. Получаемый
же при решении оптимизационной задачи наблюдаемый оператор
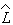 будет
естественно зависеть от
будет
естественно зависеть от  .
Следовательно, необходимо искать наблюдаемую оценку
.
Следовательно, необходимо искать наблюдаемую оценку  .
Наконец, необходима явная связь динамических переменных
поля с различными условиями его наблюдения (в частности,
масштабом несущих, пространственной ориентацией по отношению
к детектирующему устройству). Такую связь дают различные
представления состояний поля.
.
Наконец, необходима явная связь динамических переменных
поля с различными условиями его наблюдения (в частности,
масштабом несущих, пространственной ориентацией по отношению
к детектирующему устройству). Такую связь дают различные
представления состояний поля.
2.
Представление состояний классических электромагнитных
полей.
Наблюдаемые
в различных экспериментах на некоторой плоской апертуре
D (координаты r ={x,y,z=0} Î D)
детектирующего устройства классические электромагнитные
поля полностью описываются векторным потенциалом A(r,t).
Обычно экспериментально детектируют физические величины,
непосредственно связанные с электрическим вектором поля
Е = -дA/дt [2]. Переход к дискретному
описанию поля и его соответствующему гамильтонову представлению
как динамического объекта с набором {Q ,
P
,
P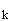 }
канонических динамических переменных (координат и импульсов)
осуществляется разложением векторного потенциала поля на
апертуре D по т. н. пространственно-временным модам
(a
}
канонических динамических переменных (координат и импульсов)
осуществляется разложением векторного потенциала поля на
апертуре D по т. н. пространственно-временным модам
(a (t)
и u
(t)
и u (r)):
A(r,t) =
(r)):
A(r,t) = 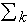 {a
{a (t)
u
(t)
u (r)+a
(r)+a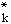 (t)
u
(t)
u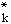 (r)}.
Канонические переменные поля связаны с временными модами
соотношениями:
(r)}.
Канонические переменные поля связаны с временными модами
соотношениями:
Q (t)={a
(t)={a (t)+a
(t)+a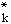 (t)},P
(t)},P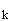 (t)=-
дQ
(t)=-
дQ /дt
= -iw {a
/дt
= -iw {a (t)
- a
(t)
- a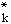 (t)},
где w = | k| с, а с - скорость света.
Соответственно функция Гамильтона поля À =
(t)},
где w = | k| с, а с - скорость света.
Соответственно функция Гамильтона поля À = 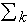 À
À
 = (1/2)
= (1/2)
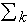 (|
P
(|
P |
|
 + w
+ w
 |
Q
|
Q |
|
 ), а
канонические переменные удовлетворяют каноническим уравнениям
Гамильтона: дQ
), а
канонические переменные удовлетворяют каноническим уравнениям
Гамильтона: дQ /дt
=дÀ /дP
/дt
=дÀ /дP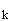 ,
дP
,
дP /дt
=дÀ /дQ
/дt
=дÀ /дQ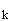 .
Тем самым, Q
.
Тем самым, Q и P
и P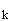 удовлетворяют временным осцилляторным уравнениям типа
д
удовлетворяют временным осцилляторным уравнениям типа
д Q
Q /дt
/дt +
w
+
w  Q
Q = 0 и описываются гармоническими функциями: Q
= 0 и описываются гармоническими функциями: Q (t)=Q
(t)=Q (0)´
cos(w t+a
(0)´
cos(w t+a 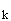 ),
P
),
P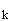 (t)=-w
Q
(t)=-w
Q (0)
sin(w t+a
(0)
sin(w t+a 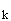 ).
).
Каждая
пара динамических канонических переменных поля {Q ,P
,P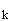 }
описывает четырехмерную область его динамического фазового
пространства - фазовый портрет в виде:
}
описывает четырехмерную область его динамического фазового
пространства - фазовый портрет в виде:
|
P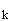 (t)|
(t)|
 + w
+ w
 |
Q
|
Q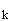 (t)|
(t)|
 =À
=À
 =w
=w
 |
Q
|
Q (0)|
(0)|
 [2].
Соответствующие пространственные моды поля u
[2].
Соответствующие пространственные моды поля u (r)
удовлетворяют пространственным осцилляторным уравнениям
д
(r)
удовлетворяют пространственным осцилляторным уравнениям
д u
u /дr
/дr +
| k|
+
| k|  u
u =
0. В приближении плоских волн, падающих на апертуру D,
что соответствует большинству экспериментов с полем, пространственные
моды также описываются гармоническими функциями: u
=
0. В приближении плоских волн, падающих на апертуру D,
что соответствует большинству экспериментов с полем, пространственные
моды также описываются гармоническими функциями: u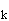 (r)=exp(ikr+b
(r)=exp(ikr+b
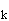 ). Поэтому
данные моды можно связать со структурными каноническими
перемененными поля, которые описывают структурное фазовое
пространство [18].
). Поэтому
данные моды можно связать со структурными каноническими
перемененными поля, которые описывают структурное фазовое
пространство [18].
Объединим
динамические и структурные канонические переменные поля,
перейдя к пространственно-временным каноническим перемененным:
Q (r,t)
= Q
(r,t)
= Q (0)
cos(w t+kr+j
(0)
cos(w t+kr+j 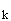 ),
P
),
P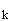 (r,t)
= -w Q
(r,t)
= -w Q (0)
sin(w t+kr+j
(0)
sin(w t+kr+j 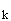 ).
Тогда соответствующее полю фазовое пространство будет описываться
набором фазовых портретов:
).
Тогда соответствующее полю фазовое пространство будет описываться
набором фазовых портретов:
{|
P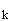 (r,t)|
(r,t)|
 + w
+ w
 |
Q
|
Q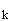 (r,t)|
(r,t)|
 = w
= w
 |
Q
|
Q (0)|
(0)|
 }. Это
означает, что в любой фиксированной пространственной точке
r апертуры D детектирующего устройства (rÎ
D) поле ведет себя, как набор осцилляторов, а в любой
фиксированный момент времени t поле ведет себя, как набор
волн. Полное поле описывается векторным потенциалом и электрической
напряженностью:
}. Это
означает, что в любой фиксированной пространственной точке
r апертуры D детектирующего устройства (rÎ
D) поле ведет себя, как набор осцилляторов, а в любой
фиксированный момент времени t поле ведет себя, как набор
волн. Полное поле описывается векторным потенциалом и электрической
напряженностью:
A(r,t)
= 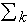 Q
Q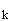 (r,t)
=
(r,t)
= 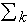 Q
Q (0)
cos(w t + kr + j
(0)
cos(w t + kr + j 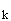 ),
),
E(r,t)=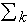 P
P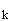 (r,t)=-
(r,t)=-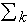 w
Q
w
Q (0)sin(w
t + kr + j
(0)sin(w
t + kr + j 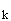 ),
(2.1)
),
(2.1)
которые
являются, по существу, обобщенными каноническими перемененными
{A(r,t), E(r,t)}.
В
классической механике состояние динамической системы, как
известно, определяется заданием начальных координат и импульсов
{Q (0),P
(0),P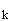 (0)}.
В обобщенном фазовом пространстве {A, E} изображающая
точка системы двигается по определенной траектории, хотя
в каждом подпространстве {Q
(0)}.
В обобщенном фазовом пространстве {A, E} изображающая
точка системы двигается по определенной траектории, хотя
в каждом подпространстве {Q ,P
,P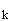 }
она движется по эллипсу. Как видно из (2.1), данная траектория
целиком и однозначно определяется набором {Q
}
она движется по эллипсу. Как видно из (2.1), данная траектория
целиком и однозначно определяется набором {Q (0),
(0),
j
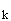 } спектральных
амплитуд и начальных фаз пространственно-временных мод поля.
Данному набору в обобщенном фазовом пространстве будет соответствовать
начальная точка {A(r,0), E(r,0)}. Тем
самым, наборы начальных условий: {Q
} спектральных
амплитуд и начальных фаз пространственно-временных мод поля.
Данному набору в обобщенном фазовом пространстве будет соответствовать
начальная точка {A(r,0), E(r,0)}. Тем
самым, наборы начальных условий: {Q (0),
P
(0),
P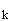 (0)}
Þ {Q
(0)}
Þ {Q (0),
j
(0),
j 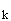 }
Þ {A(r,0), E(r,0)} являются
эквивалентными описаниями состояния полностью детерминированного
или когерентного поля. Частично когерентным или хаотическим
(тепловым) полям будут соответствовать некоторые распределения
вероятностей p[{Q
}
Þ {A(r,0), E(r,0)} являются
эквивалентными описаниями состояния полностью детерминированного
или когерентного поля. Частично когерентным или хаотическим
(тепловым) полям будут соответствовать некоторые распределения
вероятностей p[{Q (0),P
(0),P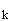 (0)}]
и р[{Q
(0)}]
и р[{Q (0),j
(0),j
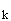 }] начальных
значений канонических переменных поля. Данные распределения
порождают и соответствующее распределение вероятностей р[{A(r,t),E(r,t)}]
траекторий в sin {A,E}.
}] начальных
значений канонических переменных поля. Данные распределения
порождают и соответствующее распределение вероятностей р[{A(r,t),E(r,t)}]
траекторий в sin {A,E}.
Множество
данных траекторий можно было бы рассматривать, как обобщенное
описание пространственно-временной структуры огибающей поля.
Однако необходимо учесть ограничения, возникающие из-за
различных условий наблюдения поля. Информативное описание
поля не должно зависеть от его несущих , т.е. от положения
спектральных амплитуд его мод на осях временных и пространственных
частот. Из (2.1) видно, что при изменении временных частот
поля и таком же изменении пространственных частот (в силу
соотношения w = | k| с) форма кривых
в подпространстве {A,E} будет изменяться.
Изменение масштаба временной несущей поля может происходить
в результате эффекта Допплера, а изменение масштаба пространственной
несущей может быть связано с изменением угла падения поля
на апертуру D детектирующего устройства, формирующего
спектр
пространственных
частот поля, или же изменением его фокусного расстояния
в случае формирования изображений.
Для
масштабно-инвариантного представления обобщенного фазового
пространства поля произведем каноническое преобразование
его координат и импульсов: Q Þ Q
Þ Q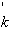 =
w Q
=
w Q ,
P
,
P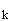 Þ P
Þ P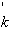 =
P
=
P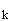 [18].
В результате получим набор инвариантных фазовых портретов
поля | P
[18].
В результате получим набор инвариантных фазовых портретов
поля | P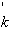 (r,t)|
(r,t)|
 + |
Q
+ |
Q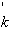 (r,t)|
(r,t)|
 =|
Q
=|
Q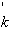 (0)|
(0)|
 , не
зависящих явно от его временных и пространственных частот.
Соответствующие им обобщенные координаты и импульсы поля
будут описываться, как:
, не
зависящих явно от его временных и пространственных частот.
Соответствующие им обобщенные координаты и импульсы поля
будут описываться, как:
H(r,t)
= 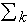 Q
Q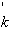 (r,t)
=
(r,t)
= 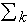 w Q
w Q (0)
cos(w t + kr + j
(0)
cos(w t + kr + j 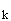 ),
),
E(r,t)
= 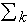 P
P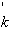 (r,t)
= -
(r,t)
= - 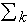 w Q
w Q (0)
sin(w t + kr + j
(0)
sin(w t + kr + j 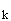 ),
(2.2)
),
(2.2)
Легко
заметить, что оба поля в (2.2) связаны взаимным преобразованием
Гильберта [19] (cos(w t+kr+j 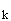 )Þ
-sin(w t+kr+j
)Þ
-sin(w t+kr+j 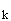 ),
sin(w t+kr+j
),
sin(w t+kr+j 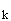 )
Þ cos(w t+kr+j
)
Þ cos(w t+kr+j 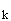 )
как по временным, так и пространственным аргументам. Поэтому
распределение р[E(r,t), H(r,t)],
описывающее в четырехмерном пространстве {E
)
как по временным, так и пространственным аргументам. Поэтому
распределение р[E(r,t), H(r,t)],
описывающее в четырехмерном пространстве {E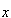 ,E
,E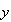 ,H
,H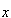 ,H
,H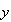 }
состояние пространственно-временной структуры огибающей
поля, инвариантно к изменению масштаба как временной, так
и пространственной несущей поля [18,20].
}
состояние пространственно-временной структуры огибающей
поля, инвариантно к изменению масштаба как временной, так
и пространственной несущей поля [18,20].
Полученные
с помощью канонического преобразования динамические переменные
(2.2) поля являются ни чем иным, как действительными компонентами
введенного Д. Габором комплексного представления поля (комплексного
аналитического сигнала) E (r,t)
= [E(r,t) + i H(r,t)] [21].
При этом произвольное комплексное поле, наблюдаемое на апертуре
D детектирующего устройства, обычно разлагается в
соответствии с (2.2) по бегущим пространственно-временным
модам E
(r,t)
= [E(r,t) + i H(r,t)] [21].
При этом произвольное комплексное поле, наблюдаемое на апертуре
D детектирующего устройства, обычно разлагается в
соответствии с (2.2) по бегущим пространственно-временным
модам E (r,t)=
(r,t)=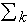 С
С u
u (r)exp(-iw
t) и полностью определяется набором {С
(r)exp(-iw
t) и полностью определяется набором {С }
своих комплексных амплитуд, заданных с некоторым распределением
р[{С
}
своих комплексных амплитуд, заданных с некоторым распределением
р[{С }]
вероятностей их значений.
}]
вероятностей их значений.
Легко
заметить, что данное распределение полностью аналогично
распределению р[E(r,t), H(r,t)]
[2]. В [22] показано, что данные распределения описывают
статистику как стационарных, так и нестационарных сигналов
любой колебательной природы, которая учитывает причинные
фазовые соотношения в чередовании компонент сигналов. Тем
самым любому изменению формы огибающей сигналов будет соответствовать
свое статистическое распределение. Более подробно вопросы
однозначной связи форм огибающих сигналов и полей с рассмотренной
статистикой исследованы в диссертации Ю.Дружинина [23].
3.
Представление состояний квази-классических электромагнитных
полей. Когерентные состояния поля.
Разложение
комплексного поля по ортогональным пространственно - временным
модам является широко известным в электродинамике представлением
поля по когерентным состояниям - состояниям с определенными
значениями спектральных амплитуд {С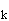 }
[1,2]. Перемешивая эти состояния с вероятностным законом
р[{С
}
[1,2]. Перемешивая эти состояния с вероятностным законом
р[{С }],
возможно получить любые квази-когерентные или же полностью
стохастические состояния поля. Для когерентных состояний
характерно наибольшее знание о структуре поля. Очевидно,
что для них р[{С
}],
возможно получить любые квази-когерентные или же полностью
стохастические состояния поля. Для когерентных состояний
характерно наибольшее знание о структуре поля. Очевидно,
что для них р[{С }]
=
}]
= 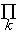 d
d
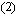 (C
(C -C
-C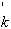 ),
где d
),
где d 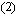 (C
(C )
= d (Re C
)
= d (Re C )
d (Im C
)
d (Im C ),
d (.) - дельта функция Дирака, а {C
),
d (.) - дельта функция Дирака, а {C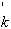 }
- набор комплексных амплитуд когерентного поля.
}
- набор комплексных амплитуд когерентного поля.
Как
показал Глаубер [2], описания р[{С }]
и р[E(r,t), H(r,t)] состояний
полей связаны соотношением:
}]
и р[E(r,t), H(r,t)] состояний
полей связаны соотношением:
р[E(r,t),H(r,t)]=
 р[{С
р[{С }]d
}]d
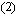 [E
[E (r,t)
(r,t)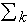 С
С u
u (r)
(r)
exp(-iw
t)] d
d C
C ,
(3.1)
,
(3.1)
где
d  [E
[E ]
= d [E] d [H], а d
]
= d [E] d [H], а d C
C = dRe C
= dRe C dIm C
dIm C .
При этом данные описания состояний полей полностью эквивалентны,
так как определяют одинаковые средние значения á L[E
.
При этом данные описания состояний полей полностью эквивалентны,
так как определяют одинаковые средние значения á L[E (r,t]ñ
любой физической величины L[E
(r,t]ñ
любой физической величины L[E (r,t],
зависящей от поля произвольным образом:
(r,t],
зависящей от поля произвольным образом:
á
L[E (r,t]ñ
=
(r,t]ñ
= 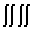 р[{С
р[{С }]
L[E
}]
L[E (C
(C )]
)]
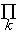 d
d C
C =
=
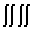 р[E(r,t),H(r,t)]
L[E
р[E(r,t),H(r,t)]
L[E (r,t)]
dE dH. (3.2)
(r,t)]
dE dH. (3.2)
При
рассмотрении поля в квазиклассическом пределе физическим
величинам E и
C
и
C необходимо
ставить в соответствие оператор
необходимо
ставить в соответствие оператор 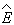
 поля и оператор
поля и оператор 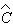
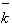 уничтожения кванта в к-ой моде поля. Тогда когерентные
состояния поля будут описываться в обозначениях Дирака волновыми
функциями | C
уничтожения кванта в к-ой моде поля. Тогда когерентные
состояния поля будут описываться в обозначениях Дирака волновыми
функциями | C ñ
, являющимися собственными функциями операторов
ñ
, являющимися собственными функциями операторов 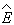
 и
и 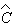
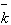 с собственными значениями соответственно E
с собственными значениями соответственно E и
C
и
C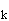 . Состояние
поля в квази-классическом пределе описывается его оператором
плотности
. Состояние
поля в квази-классическом пределе описывается его оператором
плотности  в т.н. "р" - представлении [2]:
в т.н. "р" - представлении [2]:
 =
=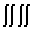 р[{С
р[{С }]|
{C
}]|
{C }ñ
á {C
}ñ
á {C }|
}|
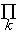 d
d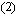 C
C ,
(3.3)
,
(3.3)
где
| {C }ñ
=
}ñ
= 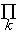 |
C
|
C ñ
- волновая функция чистого когерентного состояния поля.
Заметим, что под оператором
ñ
- волновая функция чистого когерентного состояния поля.
Заметим, что под оператором 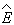
 понимаются два оператора: Re
понимаются два оператора: Re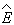
 =
=
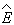 и Im
и Im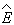
 =
=
 . С позиции
квантовых измерений любая процедура получения спектра собственных
значений F и G каких-либо совместно измеряемых операторов
. С позиции
квантовых измерений любая процедура получения спектра собственных
значений F и G каких-либо совместно измеряемых операторов
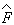 и
и
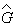 ,
связанных с полем, порождает операторно-вероятностную меру
| F,Gñ á F,G| , определяемую с помощью
собственных функций | F,Gñ данных операторов [15].
Эта мера определяет совместную плотность вероятности р[F,G]
спектра собственных значений F и G в поле, находящемся в
состоянии, описываемом оператором плотности
,
связанных с полем, порождает операторно-вероятностную меру
| F,Gñ á F,G| , определяемую с помощью
собственных функций | F,Gñ данных операторов [15].
Эта мера определяет совместную плотность вероятности р[F,G]
спектра собственных значений F и G в поле, находящемся в
состоянии, описываемом оператором плотности 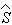 по известной квантомеханической схеме: р[F,G] = Tr[
по известной квантомеханической схеме: р[F,G] = Tr[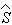 | F,Gñ á F,G| ]. Используя "р"- представление
(3.3), можно получить [24]:
| F,Gñ á F,G| ]. Используя "р"- представление
(3.3), можно получить [24]:
р[F,G]=
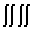 р[{С
р[{С }]|
á {C
}]|
á {C }|
F,Gñ |
}|
F,Gñ | 
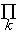 d
d C
C ,
(3.4)
,
(3.4)
где
положительно определенная величина| á {C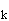 }|
F,Gñ |
}|
F,Gñ |  показывает
степень "перекрытия" собственных функций измеряемых операторов
с волновыми функциями когерентного состояния поля. В нашем
случае в качестве операторов
показывает
степень "перекрытия" собственных функций измеряемых операторов
с волновыми функциями когерентного состояния поля. В нашем
случае в качестве операторов 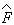 и
и
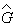 необходимо
использовать операторы самого поля
необходимо
использовать операторы самого поля 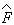 =
= 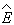 и
и
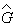 =
=  с общими собственными функциями | {C
с общими собственными функциями | {C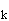 }ñ
. Используя условие "перекрытия" различных когерентных состояний
(| C
}ñ
. Используя условие "перекрытия" различных когерентных состояний
(| C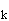 ñ
и | C
ñ
и | C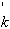 ñ
) [2]:
ñ
) [2]:
|
á C |
C
|
C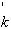 ñ
|
ñ
| 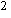 =
exp(- | C
=
exp(- | C -C
-C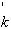 |
|
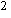 ) , из
(3.4) легко получить [24]:
) , из
(3.4) легко получить [24]:
р[E(r,t),H(r,t)]
= р[{С
р[{С }]
}]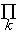 exp(-|
C
exp(-|
C -C
-C |
|
 ) d
) d C
C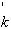 .
(3.5)
.
(3.5)
Полученное
представление (3.5) описания пространственно-временной структуры
квази-классического поля совпадает с представлением (3.1)
описания классического поля. Оба представления являются
редуцированными оценками многомерной плотности вероятности
р[{С }]
набора {С
}]
набора {С }
комплексных амплитуд поля. Однако, поскольку описание (3.5)
получено непосредственно с помощью неэрмитового оператора
}
комплексных амплитуд поля. Однако, поскольку описание (3.5)
получено непосредственно с помощью неэрмитового оператора
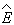 , то
видно, что p[E,H] не является наблюдаемой
оценкой [24]. Поэтому для вычисления средних значений наблюдаемых
физических величин по схеме
, то
видно, что p[E,H] не является наблюдаемой
оценкой [24]. Поэтому для вычисления средних значений наблюдаемых
физических величин по схеме
(3.1)
необходимо перейти к наблюдаемому описанию пространственно-временной
структуры поля.
4.
Наблюдаемое описание пространственно-временной структуры
когерентного поля.
Наблюдаемое
описание пространственно-временной структуры электромагнитного
поля может быть получено из (3.4) выбором связанных с полем
E (r,t)
наблюдаемых физических величин F и G, операторы которых
являются эрмитовыми. Для этого операторы физических величин
должны зависеть от нормально упорядоченных произведений
(r,t)
наблюдаемых физических величин F и G, операторы которых
являются эрмитовыми. Для этого операторы физических величин
должны зависеть от нормально упорядоченных произведений
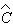
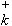
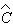
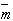 операторов рождения и уничтожения квантов в различных модах
(k, m) поля, а сами величины должны зависеть
от произведения E
операторов рождения и уничтожения квантов в различных модах
(k, m) поля, а сами величины должны зависеть
от произведения E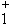 (r,t)
E
(r,t)
E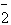 (r,t)
комплексно сопряженных полей, формируемых данными модами:
F[E
(r,t)
комплексно сопряженных полей, формируемых данными модами:
F[E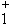 (r,t)
E
(r,t)
E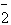 (r,t)]
и G[E
(r,t)]
и G[E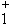 (r,t)
E
(r,t)
E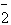 (r,t)]
[25]. Тогда, осуществляя при измерении физической величины
L в (3.2) замену переменных, можно получить [24,26]:
(r,t)]
[25]. Тогда, осуществляя при измерении физической величины
L в (3.2) замену переменных, можно получить [24,26]:
á
Lñ =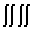 р[E(r,t),H(r,t)]L[F,G]
dE dH=
р[E(r,t),H(r,t)]L[F,G]
dE dH=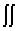 р[F,G]
J
р[F,G]
J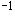 L[E
L[E (r,t)]dF
dG,
(r,t)]dF
dG,
где
якобиан преобразования J = (¶ F/¶ E)(¶
G/¶ H)-(¶ F/¶ H)(¶ G/¶
E). Отсюда, при J ¹ 0 получается искомое наблюдаемое
описание состояния пространственно-временной структуры или
формы огибающей поля в виде распределения р[F,G] J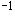 [24]. Как и исходное ненаблюдаемое описание, оно является
редуцированной наблюдаемой оценкой (3.4) оператора плотности
(3.3) поля. Интегрируя данное распределение по всей двумерной
апертуре D детектирующего устройства, возможно получить
обобщенное описание формы огибающей поля на плоскости:
[24]. Как и исходное ненаблюдаемое описание, оно является
редуцированной наблюдаемой оценкой (3.4) оператора плотности
(3.3) поля. Интегрируя данное распределение по всей двумерной
апертуре D детектирующего устройства, возможно получить
обобщенное описание формы огибающей поля на плоскости:
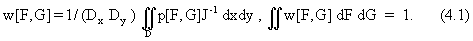 Частным
случаем (4.1) является описание только временной огибающий
поля в выбранной пространственной моде поля. В этом случае
апертура D детектирующего устройства должна быть
согласована с данной модой поля. Двумерное распределение
w[F,G] является фазовым портретом пространственно-временной
структуры огибающей когерентного поля [24, 26].
Частным
случаем (4.1) является описание только временной огибающий
поля в выбранной пространственной моде поля. В этом случае
апертура D детектирующего устройства должна быть
согласована с данной модой поля. Двумерное распределение
w[F,G] является фазовым портретом пространственно-временной
структуры огибающей когерентного поля [24, 26].
Физический
смысл фазового портрета заключается в том, что он отображает
частоту w совместных событий, при которых детектирующим
устройством регистрируются физические величины F и G, связанные
с наблюдаемым на его апертуре полем.
В
[26] рассмотрены различные случаи выбора физических величин
F и G, для которых J ¹ 0. С помощью (3.1,3.5) легко
показать, что вероятностное распределение р[E(r,t),H(r,t)]
хаотических или полностью некогерентных полей вырождается
в одномерное р[E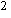 (r,t)+H
(r,t)+H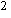 (r,t)],
зависящее лишь от интенсивности поля. В этом случае информация
о форме огибающий поля теряется (J = 0), фазовый портрет
не имеет смысла, а наибольшая информация о состоянии поля
содержится в его спектральных или корреляционных функциях
[25, 26].
(r,t)],
зависящее лишь от интенсивности поля. В этом случае информация
о форме огибающий поля теряется (J = 0), фазовый портрет
не имеет смысла, а наибольшая информация о состоянии поля
содержится в его спектральных или корреляционных функциях
[25, 26].
Для
когерентных и квази-когерентных полей аппарат спектральных
и корреляционных функций также нашел широкое применение,
в частности, для описания степени их когерентности [1,2].
Однако все эти описания теряют важные фазовые соотношения
во взаимном расположении компонент (отсчетов) пространственных
или временных огибающих поля [22,26]. Данная информация
присутствует лишь в фазовом портрете поля.
5.
Физически-оптимальный детектор пространственно-временной
структуры огибающей когерентного поля.
С
использованием полученной наблюдаемой оценки оператора плотности
поля рассмотренная в п.1 оптимизационная задача может быть
сформулирована следующим образом. Необходимо найти вид зависящей
от поля E (r,t)
= [E(r,t) + i H(r,t)] физической
величины L, которая максимизирует критерий Фишера
(r,t)
= [E(r,t) + i H(r,t)] физической
величины L, которая максимизирует критерий Фишера
F
(L) = s 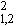 / s
/ s 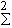 = s
= s 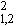 / (s
/ (s 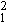 +s
+s
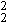 ), где:
), где:
s
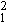 =
=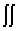 w
w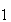 [F,G]
(L- á L
[F,G]
(L- á L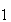 ñ
)
ñ
)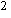 dF
dG, s
dF
dG, s 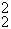 =
=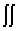 w
w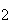 [F,G]
(L- á L
[F,G]
(L- á L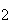 ñ
)
ñ
)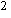 dF
dG,
dF
dG,
s
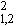 =(á
L
=(á
L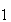 ñ
-á L
ñ
-á L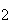 ñ
)
ñ
)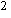 ,á
L
,á
L ñ
=
ñ
=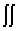 w
w [F,G]LdFdG,
(5.1)
[F,G]LdFdG,
(5.1)
а
w [F,G]
- наблюдаемые оценки операторов
[F,G]
- наблюдаемые оценки операторов 
 плотности поля в состояниях (1 и 2) с различными пространственно-временными
формами огибающий. В силу (3.4) и своего определения (4.1)
w
плотности поля в состояниях (1 и 2) с различными пространственно-временными
формами огибающий. В силу (3.4) и своего определения (4.1)
w [F,G]
удовлетворяют условию нормирования
[F,G]
удовлетворяют условию нормирования 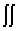 w
w [F,G] dF dG = 1,
[F,G] dF dG = 1, 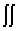 (w
(w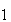 -
w
-
w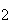 ) dF
dG = 0.
) dF
dG = 0.
Все
выражения в (5.1) можно упростить, заменяя интегрирование
по переменным F и G суммированием по условному индексу q
= {F,G}. Тогда критерий Фишера можно выразить в виде:
F
(L)=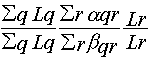 ,
где L
,
где L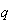 =L[F,G],
(5.2)
=L[F,G],
(5.2)
a 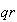 = [w
= [w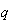 (1)-w
(1)-w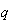 (2)][w
(2)][w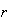 (1)
- w
(1)
- w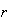 (2)],
b
(2)],
b 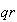 = [w
= [w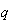 (1)+w
(1)+w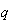 (2)]
d
(2)]
d 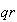 -
[w
-
[w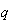 (1)w
(1)w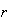 (1)
+ w
(1)
+ w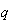 (2)w
(2)w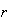 (2)],
w
(2)],
w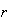 (1,2)
= w
(1,2)
= w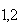 [F,G].
Выражение (5.2) хорошо известно в математической физике,
как обобщенное число Релея. Известно также решение, максимизирующее
это число [27]:
[F,G].
Выражение (5.2) хорошо известно в математической физике,
как обобщенное число Релея. Известно также решение, максимизирующее
это число [27]:
L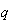 =
g
=
g 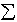
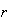 b
b
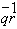 [w
[w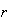 (1)-w
(1)-w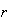 (2)],
g =
(2)],
g =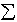
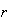 L
L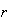 [w
[w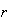 (1)
- w
(1)
- w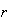 (2)].
(5.3)
(2)].
(5.3)
Для
нахождения явного вида (5.3) необходимо обратить матрицу
b 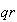 .
Это можно сделать с помощью итерационной процедуры, вводя
значение меры различия состояний:
.
Это можно сделать с помощью итерационной процедуры, вводя
значение меры различия состояний:
m
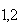 =
=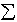
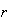 w
w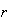 (1)[w
(1)[w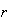 (1)-w
(1)-w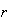 (2)]
(2)]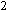 /w
/w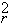 (1)=
m
(1)=
m 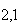 =
=
=
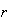 w
w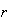 (2)[w
(2)[w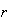 (1)
- w
(1)
- w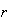 (2)]
(2)] /w
/w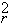 (2).
(2).
Тогда:
L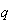 =[1-m
=[1-m
 (1-m
(1-m
 )/10]
)/10]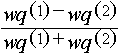 (5.4)
(5.4)
Исходя
из (5.4) и возвращаясь к исходным обозначениям, получим:
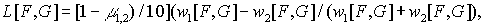
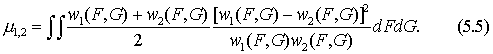
Таким
образом, физически-оптимальный детектор пространственно-временной
структуры огибающей когерентного поля выражается через фазовые
портреты полей в различных состояниях и меру их различия.
Используя
(5.1) и (5.5) получим средние значения и дисперсии физической
величины, измеряемой найденным оптимальным детектором, в
различных состояниях:
á
L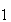 ñ
=(m
ñ
=(m  /4)[1-m
/4)[1-m
 (1-m
(1-m
 )/10],
á L
)/10],
á L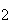 ñ
=-(m
ñ
=-(m  /4)[1-m
/4)[1-m
 (1- m
(1- m
 )/10],
s
)/10],
s 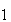 = s
= s 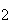 = {m
= {m  [1-
m
[1-
m  (1-
m
(1-
m  )/10]}
)/10]}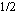 /2
. (5.6)
/2
. (5.6)
Физический
смысл полученного детектора можно пояснить с по мощью рис.1,
где показаны: векторы w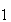 и w
и w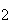 ,
соответствующие фазовым портретам w
,
соответствующие фазовым портретам w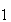 [F,G]
и w
[F,G]
и w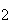 [F,G]
известных или эталонных состояний (
[F,G]
известных или эталонных состояний (
 );
вектор L, описывающий действие детектора (5.5) и
определяемый своими компонентами (5.4); вектор w
);
вектор L, описывающий действие детектора (5.5) и
определяемый своими компонентами (5.4); вектор w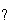 ,
соответствующий фазовому портрету неизвестного исследуемого
состояния
,
соответствующий фазовому портрету неизвестного исследуемого
состояния  .
Видно, что физически-оптиальный детектор описывается вектором
L, ортогональным вектору (w
.
Видно, что физически-оптиальный детектор описывается вектором
L, ортогональным вектору (w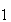 +
w
+
w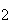 )
и практически коллинеарным вектору (w
)
и практически коллинеарным вектору (w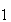 -
w
-
w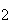 ).
Мерой коллинеарности является мера различия состояний: L(w
).
Мерой коллинеарности является мера различия состояний: L(w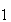 -
w
-
w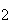 )
= m
)
= m  /2.
/2.
Степень
близости неизвестного и эталонного состояний определяется
знаком и величиной проекции вектора w на вектор L.
на вектор L.
Исходя
из (5.6) и считая, что измеряемые физически-оптимальным
детектором (5.5) величины распределены по нормальному закону,
легко графически представить плотности вероятностей значений
измеряемой физической величины в различных состояниях поля
(см. рис.2).
Заштрихованная
область пересечения распределений вероятностей p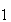 [<L>]
@ exp[-(<L> - á L
[<L>]
@ exp[-(<L> - á L ñ
)
ñ
) /2s
/2s
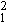 ] и p
] и p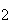 [<L>]
@ exp[-(<L> - á L
[<L>]
@ exp[-(<L> - á L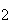 ñ
)
ñ
)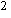 /2s
/2s
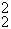 ] соответствует
максимальной ошибке М различения состояний поля. Приближенно
можно считать, что М
] соответствует
максимальной ошибке М различения состояний поля. Приближенно
можно считать, что М
£
(1-m  /2)/2m
/2)/2m
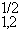 . Так,
например, для наиболее различающихся состояний с неперекрывающимися
фазовыми портретами (m
. Так,
например, для наиболее различающихся состояний с неперекрывающимися
фазовыми портретами (m  = 1) М £ 0,25. Поэтому для уменьшения ошибки отнесения
неизвестного состояния поля (
= 1) М £ 0,25. Поэтому для уменьшения ошибки отнесения
неизвестного состояния поля ( )
с средним значением <L> к какому- либо известному
состоянию (
)
с средним значением <L> к какому- либо известному
состоянию (
 )
необходимо выбирать порог классификации <L
)
необходимо выбирать порог классификации <L >
> 0 и действовать по решающему правилу, принятому в
методах технически-оптимального синтеза устройств [6, 8-12]:
>
> 0 и действовать по решающему правилу, принятому в
методах технически-оптимального синтеза устройств [6, 8-12]:
-
если <L> ³ <L >,
то поле находится в состоянии
>,
то поле находится в состоянии 
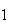 ;
;
-
если <L> £ - <L >,
то поле находится в состоянии
>,
то поле находится в состоянии 
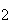
Заключение.
Необходимость
экспериментального наблюдения различных состояний электромагнитных
полей, отличающихся формой огибающих, приводит
к
задаче физически-оптимального синтеза устройств детектирования
поля. Для когерентных полей физически-оптимальной является
процедура детектирования, основанная на регистрации т.н.
фазового портрета w[F,G] поля, регистрируемого в
виде двумерного частотного распределения w независимых физических
величин F[E(r,t), H(r,t)] и
G[E(r,t),H(r,t)], каждая из
которых функционально связана c пространственно-временными
модами E(r,t) и H(r,t) действительной
и мнимой компонент комплексного когерентного поля E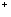 (r,t),
наблюдаемого в момент времени t на апертуре D(r
Î D) детектирующего устройства. Формируемый фазовый
портрет является наблюдаемой оценкой оператора плотности
когерентного поля, которая определяется формой его пространственно-временной
огибающей. Фазовые портреты w[F,G] когерентных и частично
когерентных полей отражают закономер-ности в чередовании
отсчетов их пространственных или временных огибающих.
(r,t),
наблюдаемого в момент времени t на апертуре D(r
Î D) детектирующего устройства. Формируемый фазовый
портрет является наблюдаемой оценкой оператора плотности
когерентного поля, которая определяется формой его пространственно-временной
огибающей. Фазовые портреты w[F,G] когерентных и частично
когерентных полей отражают закономер-ности в чередовании
отсчетов их пространственных или временных огибающих.
В
отличие от технически-оптимальных методов синтеза детекторов
когерентных полей, при которых регистрируемые пространственно-временные
моды E(r,t) действительных компонент поля
сравниваются с модами E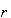 (r,t)
аналогичных компо-
(r,t)
аналогичных компо-
нент
эталонных полей (r = 1,2,... R) [11-13], при физически-оптимальном
синтезе сравниваются фазовые портреты w[F,G] и w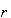 [F,G]
огибающих анализируемого и эталонных полей. Результаты
последнего сравнения в силу специального выбора функций
F и G инвариантны к условиям наблюдения полей [20, 23, 28].
Сами фазовые портреты, регистрируемые в наблюдаемом поле,
могут в дальнейшем использоваться как исходные сигналы в
известных технически-оптимальных методах их анализа.
[F,G]
огибающих анализируемого и эталонных полей. Результаты
последнего сравнения в силу специального выбора функций
F и G инвариантны к условиям наблюдения полей [20, 23, 28].
Сами фазовые портреты, регистрируемые в наблюдаемом поле,
могут в дальнейшем использоваться как исходные сигналы в
известных технически-оптимальных методах их анализа.
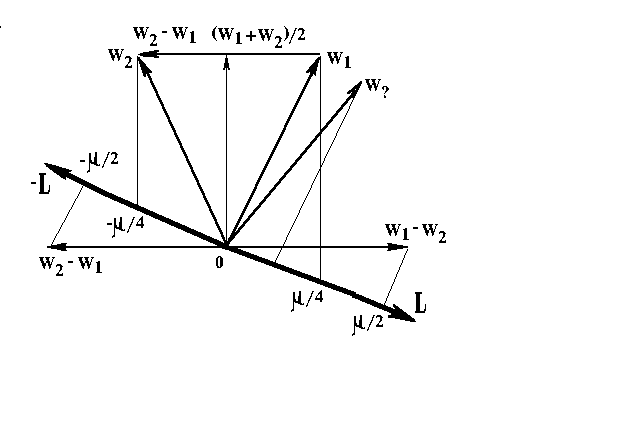
Рис.1.
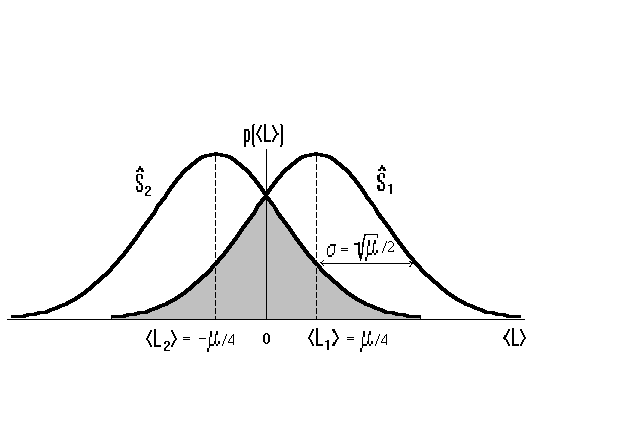
Рис.2.
В
заключение отметим, что рассмотренные свойства фазовых портретов
использованы в практических задачах оптической интерферометрии
[28], оптической микроскопии [29,30], оптической дифрактометрии
[31,32], спектроскопии оптического смешения [33,34], распознавания
оптических и радиолокационных изображений [23,35,36]. В
оптической голографической фильтрации физическая оптимизация
приводит к необходимости использования не только согласованных
фильтров Ван-дер-Люгта [37], но и объемных голографических
фильтров [38,39], наиболее полно учитывающих фазовую информацию
о когерентных полях. Практика показала, что для сложных
полей (смешанных состояний), формируемых большим количеством
различных объектов, рассмотренные методы исследования состояний
поля эффективно сочетаются с согласованной фильтрацией и
другими методами предварительной обработки полей [23,35,36,40].
ЛИТЕРАТУРА
1. Дж.Клаудер, Э.Сударшан. Основы квантовой оптики. М.:
Мир, 1970.
2. Р. Глаубер. Оптическая когерентность и статистика фотонов.
В сб.: Квантовая оптика и квантовая радиофизика. М.: Мир,
1966.
3. А.Н. Колмогоров. Интерполирование и экстраполирование
стационарных последовательностей./Известия АН СССР. Сер.
мат.,1941,т.5, N1.
4. N. Wiener. Extrapolation, interpolation and smoothing
of stationary time series. New York: J. Wiley, 1949.
5. В.А. Котельников. Теория потенциальной помехоустойчивости.
М.: Госэнергоиздат, 1958.
6. Л.А. Вайнштейн, В.Д. Зубаков. Выделение сигналов на фоне
случайных помех. М.: Сов. радио, 1960.
7. R.L. Kalman, R.S. Bucy. New results in linear filtering
and prediction theory. /J. Basic Engr. (ASME Trans.), 1961,
v. 83, D.
8.
Д.Мидлтон. Введение в статистическую теорию связи., т.1,2.
М.: Сов.радио, 1961, 1962.
9. Р.Л.Стратонович. Принципы адаптивного приема. М.:Сов.
радио,1972.
10.
В.И. Тихонов, Н.К. Кульман. Нелинейная фильтрация и квази
когерентный прием сигналов. М.: Сов. радио, 1975.
11.
В.Г. Репин, Г.П. Тартаковский. Статистический синтез при
априорной неопределенности и адаптация информационных систем.
М.:Сов. радио, 1977.
12.
I. N.Kompanets. Optical images/Image Processing in Russia.
Proc. SPIE, 1992, v.1704 (Advances in Optical Information
Processing), pp. 343-370.
13.
V.V.Dadeshidze, I.N.Kompanets, L.L.Lindunen, and A.A.Vasiliev.
Optical correlator using binary phase-only filters implemented
with hybrid TV/liquid-crystal spatial light modulators.
Proc. SPIE, 1993, vol. 2065 (Optics, Illumination, and images/Image
Sensing for Mashine Vision V111), pp. 182-191.
14.
А.S. Holevo. Statistical problems in quantum physics. Proc.
2nd Japan-USSR Symp. Prob. Theo. Kyoto, Japan, v. 1, pp.
22-40, 1972.
15.
К. Хелстром. Квантовая теория проверки гипотез и оценивания.
М.: Мир, 1979.
16.
R.A. Fischer. Contributions to mathematical statistics.
New York: John Wiley, 1950.
17.
А.С. Холево. Вероятностные и статистические аспекты квантовой
теории. М.: Наука, 1980.
18.
A.E. Krasnov, A.K. Glotov, V.F. Starodubtsev. Integral invariant
description of grey-scale images. /Mathematical Researh
(Computer Analysis of images/Images and Patterns). Berlin:
Akademia-Verlag, 1987, pp. 55-61.
19.
Э. Титчмарш. Введение в теорию интегралов Фурье. М.: ИЛ,
1948.
20.A.E.Краснов.Использование
Гильберт- фильтрации электромагнитного сигнала для выделения
инвариантных признаков его пространственной структуры. /Автометрия,
1987, v.5, стр. 102-103.
21.
D. Gabor. Jorn. Inst. Electr. Eng., v. 93, 1946, p. 429.
22.
А.Е. Краснов. Статистически причинное описание структуры
сигналов колебательной природы./ Автометрия, 1990, т.6,
стр. 15-20.
23.
Ю.О. Дружинин. Разработка и исследовавие устройств для анализа
формы изображений на основе Гильберт-фильтрации. - Автореферат
канд. диссертации, М.: ИПУ РАН, 1992.
24.
A.E. Krasnov. Method of phase portrait for analysis of nonstationary
coherent optical fields. Proc. SPIE, 1993, v.1978 (Coherent
Measuring and Data Processing Methods and Devices), pp.
193-200.
25.
М. Лекс. Флуктуации и когерентные явления. М.: Мир, 1974.
26.
A.E. Krasnov. Statistical causal description of space-time
srtucture of quasi-coherent optical fields. Proc. SPIE,
1993, v.1978 (Coherent Measuring and Data Processing Methods
and Devices), pp. 57 - 65.
27.
С. Уилкс. Математическая статистика. М.: Наука, 1967.
28.
Авт. свидет. N 1368729, Б.И. N3, 1988.
29.
А.Е.Краснов. Информативные признаки пространственной структуры
квази-стационарного электромагнитного поля. В сб.: "Оптоэлектронные
методы и средства обработки изображений". - Винница, 1987,
стр. 81-84.
30.
А.Н.Ануашвили, В.Д.Зотов, А.Е.Краснов, К.А.Яновский. О принципах
построения оптоэлектронных систем анализа изображений микроструктур.
/Автоматика и телемеханика, N1, 1989, стр. 162-170.
31.
А.Е.Краснов, Ю.О.Дружинин, А.Ф.Лунин, С.Е.Юрченко. Автоматизированный
оптический контроль цилиндрических магнитных доменов материалов.
В сб.: "Современные проблемы физики и ее приложений", М.:
ВИНИТИ, 1990, стр. 21.
32.
Авт. свидет. N5588, Б.И. N 20, 1990.
33.
A.Krasnov, A.Lunin, Yu. Druzhinin. Description of non-stationary
scattered fields in light beating spectroscopy problems.Proc.
SPIE, 1993, v.1978 (Coherent Measuring and Data Processing
Methods and Devices), pp. 66 - 76.
34.
A.Krasnov. Method of Phase Portrait for Analysis of Nonstationary
Dynamics of Coherent Optical Fields. Proc. of International
conference on advanced and laser technologies (ALT 92),
Moscow, 1992, pp. 91-94.
92),
Moscow, 1992, pp. 91-94.
35.
A.Krasnov, A.Dobrovidov, Yu.Druzhininu., G.Popova. An Informational
Technology for Investigation of Structural Dynamics of Environmental
Objects by Their Multiple-Spectral images/Images. Proc.SPIE,
1993, v.2107 (Optical Monitoring of the Environment), pp.
53-64.
36.
A.Krasnov, I.Kompanets, Yu.Druzhinin Detection and Recognition
of Spatial Medium Disturbances by Satellite images/Image
Processing.-Proc. of the European Symposium on "Satellite
Remote Sensing", 1994, v.2312 (Optics in Atmospheric Propagation
and Random Phenomena), Italy, 1994, pp. 49.
37.
A. Vander Lugt. IEEE Trans. IT-10, 1964, p.139.
38.
А.Е.Краснов. Пространственно-неинвариантные фильтры оптических
сигналов на основе объемных голограмм. / Квантовая электроника,
т. 7, N 4, 1980, стр. 818 - 828.
39.
А.Е.Краснов. Объемные голографические фильтры и их использование
в оптоэлектронных вычислительных устройствах для обработки
изображений. - Автореферат канд. диссертации, М.: ИПУ РАН,
1980.
40.
I.N.Kompanets. Optical rial time image analysis and processing
in Lebedev Physics Institute. - Proc. of Workshop for Scientists
and Technical Managers from the Former Soviet Union and
the U.S. (Exploring the Opportunities for Cooperative Research),
Orlando, Florida, U.S.A., 8-9 april, 1994, pp. 31-51.

