ПЕРЕХОДНЫЕ ПРОЦЕССЫ НА ГРАНИЦЕ РАЗДЕЛА

ДВУХ СРЕД И УСТАНОВЛЕНИЕ ФОРМУЛ ФРЕНЕЛЯ

А.А.Колоколов

Введение

Распространение электромагнитных волн с передним фронтом в линейной среде с дисперсией и формирование стационарной волны определенной частоты вместе с установлением показателя преломления, фазовой скорости и других характеристик стационарного процесса впервые были рассмотрены в работах Л.Бриллюэна и А.Зоммерфельда [1]. При падении волны с передним фронтом на границу раздела двух сред возникают поверхностные переходные процессы, описывающие возбуждение отраженной и преломленной волн и приводящие к установлению формул Френеля для плоских монохроматических волн. Впервые эти поверхностные переходные процессы рассматривались Г.В.Скроцким с сотрудниками в работе [2], где были получены важные результаты, относящиеся к отраженной волне. Однако примененный в этой работе сложный математический метод не позволил полностью проанализировать все стадии формирования стационарного отражения и оценить время установления формул Френеля.

В настоящей работе для описания границы раздела вакуум-среда используются такие хорошо известные в теории линейных систем функции как импульсный отклик и переходная характеристика. Это позволяет избежать сложных расчетов и получить общие для всех линейных отражающих сред результаты на основе принципа причинности и высокочастотной асимптотики диэлектрической проницаемости. В случае отражения волн с резким передним фронтом от плазмы и диэлектрика получены формулы, позволяющие оценить характерное время установления формул Френеля. Эти результаты позволяют определить те пределы быстродействия оптических устройств, которые обусловлены протеканием волновых процессов на границе раздела двух сред.

1. Импульсный отклик и переходная характеристика

границы раздела вакуум-среда.

Рассмотрим волну с резким передним фронтом E(z,t) распространяющуюся в вакууме в положительном направлении оси z

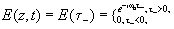(1.1)

где t - время, t - = t-z/c, c - скорость света в вакууме, i = Ö -1, w o - частота.

Если волна (1.1) падает нормально на плоскую поверхность z=0 раздела вакуума (z<0) и линейной среды (z>0) с показателем преломления n(w ), то согласно принципу суперпозиции отраженная волна запишется в виде

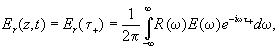(1.2.)

где t + = t+z/c, z>0. 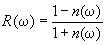- амплитудный коэффициент отражения плоской монохроматической волны с частотой w и E(w ) - фурье-образ волны (1.1).

Используя теорему о преобразовании Фурье произведения двух функций (1.2) можно переписать в виде

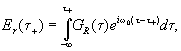(1.3)

где

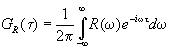(1.4)

- импульсный отклик границы раздела вакуум-среда, описывающий отраженную волну при нормальном падении дельта-импульса d (t -). Путь интегрирования в (1.4.) проходит выше всех особых точек функции R(w ).

Согласно принципу причинности амплитудный коэффициент отражения R(w ) не имеет особых точек в верхней полуплоскости комплексной частоты w , а его асимптота в области больших частот соответствует поведению электронов cреды как газа свободных частиц [3]

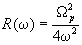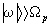, (1.5)

где 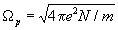- электронная плазменная частота, е и m - соответственно заряд и масса электрона, N - концентрация электронов cреды.

Следовательно, при t £ 0 путь интегрирования в (1.4.) можно замкнуть в верхней полуплоскости комплексной частоты w по полуокружности сколь угодно большого радиуса и, применяя к данному замкнутому контуру теорему Коши, получить

G_R(t )=0, t £ 0 (1.6)

и

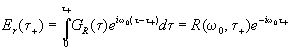(1.7.)

Здесь введена переходная характеристика границы раздела вакуум-среда на частоте w о

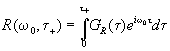(1.8.)

Из (1.8) видно, что переходная характеристика есть фурье-компонента на частоте w о текущего спектра импульсного отклика. Согласно (1.4), (1.6) и (1.8)

lim R(w о,t ₊)=R(w о), lim E_r(t ₊)=R(w о) exp(-iw _{0t +}). (1.9)

t ^{+® +¥} t ^{+® +¥}

Время выхода t _R переходной характеристики R(w о,t ₊) на стационарное значение R(w о) есть время установления формул Френеля на данной частоте (w о).

2. Характеристики переднего фронта отраженной волны.

Согласно (1.7) переходная характеристика R(w о,t ₊) есть комплексная амплитуда отраженной волны. Из (1.6)и (1.8) следует, что для всех линейных сред на переднем фронте отраженной волны t ₊=0 [2]

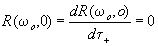. (2.1)

используя (1.8)вместе с соотношением R(-w * )=R* (w ), где * обозначает комплексное сопряжение, можно показать, что 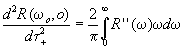(2.2) где R(w ) =R¢ ( w ) +iR¢ ¢ (w ).

Прямым следствием аналитических свойств функции R(w ) в верхней полуплоскости комплексной частоты w и асимптотики (1.5) являются соотношения Крамерса-Кронига [3]

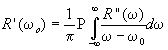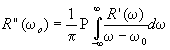, (2.3)

и правило сумм

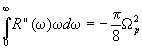(2.4)

Согласно (2.1), (2.2) и (2.4)

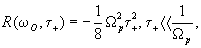(2.5)

поэтому на переднем фронте отраженной волны всегда происходит фазовый сдвиг на p , а формирование амплитуды характеризуется временем запаздывания порядка 1/W p [2].

Выполнение соотношений Крамерса-Кронига и, следовательно, принципа причинности для отраженной волны в смысле E_r(t ₊)=0 для всех t ₊<0 возможно только для комплексных значений R(w ). Комплексность функции R(w ) может быть обусловлена либо поглощением (усилением) отражающей среды (e ’’º 0), либо отрицательной величиной e ( w ) в некотором диапазоне частот в случае прозрачной среды (e ¢ ¢ º 0). В последнем случае |R(w )|=1 и в указанном диапазоне частот происходит полное отражение.

 

 

3. Отражение от плазмы

Подставляя амплитудный коэффициент отражения непоглощающей плазмы

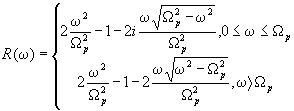(3.1)

где R(-w ) =R* ( w ) и W р -электронная плазменная частота, в (1.4) и выполняя необходимые расчеты, получим

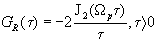(3.2)

где J₂(x) - функция Бесселя первого рода.

Асимптотика импульсного отклика (3.2) при t >>1/W p, определяющая время установления стационарного отражения t _R, имеет вид

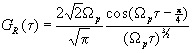(3.3)

который соответствует затухающим колебаниям на частоте W p, разделяющей области полного и частичного отражения. Затухание колебаний происходит по степенному закону и обусловлено излучением энергии преломленной волны с частотой W p в исходную среду, из которой падает волна (1.1).

Оценка времени установления стационарного отражения t _R, определяемого с помощью условия 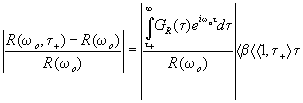(3.4)

и (3.3), дает

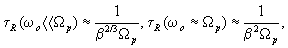
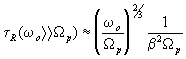(3.5)

Таким образом, величина t _R(w о) имеет локальный максимум на частоте w о=W р.

Учет слабого поглощения плазмы может изменить время t _R только в области частот w о ³ W р. Например, при w о » W р

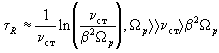(3.6)

где n _ст - частота столкновений электронов с ионами плазмы.

4. Отражение от диэлектрика

Рассмотрим отражение от среды с диэлектрической проницаемостью

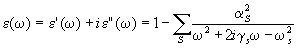(4.1)

где суммирование выполняется по всем ансамблям гармонических осцилляторов среды с частотами собственных колебаний w _S и коэффициентами затухания 0<g _S<<w _S, причем

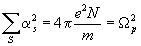(4.2)

С помощью интегрирования в комплексной плоскости частоты можно показать, что импульсный отклик границы раздела вакуум - диэлектрик

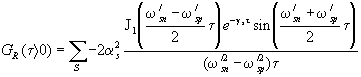(4.3)

где w _sp=w ¢ _sp+iw ¢ ¢ _sp - полюсы и w _sn=w ¢ _sn+iw ¢ ¢ _sn - нули диэлектрической проницаемости (4.1) и соответственно точки ветвления функции R(w ). Вблизи переднего фронта отраженной волны, где W _{pt +}<<1 и для всех s (w ¢ _sn+w ¢ ¢ _sn)t <<1, выражение (4.3) можно разложить в ряд по степеням t и учесть только первый линейный по t член разложения. В результате, используя (1.8) и (4.2), снова приходим к универсальной для всех линейных сред формуле (2.5).

При (w ¢ _sn-w ¢ _sр)t >>1 с помощью асимптотики J₁(x) для х>>1 импульсный отклик отдельного ансамбля осцилляторов можно записать в виде

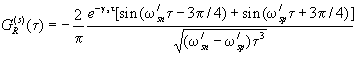(4.4)

Выражение (4.4) описывает затухающие колебания на частоте w ¢ _sn и w ¢ _sр, которые соответствуют нераспространяющимся преломленным волнам. В пределе g _s=0 эти частоты разделяют области частичного и полного (w ¢ _sр<w < w ¢ _sn) отражения. Экспотенциальный и степенной множители в (4.4) описывают затухание, обусловленное соответственно поглощением среды и излучением энергии преломленных волн с частотами w ¢ _sn и w ¢ _sр в исходную среду, т.е. вакуум.

Для оценки времени установления стационарного отражения на частоте w _о рассмотрим случай, когда в (4.3) можно ограничиться учетом вклада только одного ансамбля осцилляторов, для которого величина |w _о-w _s| является минимальной.

Расчеты t _R, выполняемые с помощью (3.4) и (4.4), проиллюстрируем двумя примерами. В области резонанса, где

|(w _о-w ¢ _sn)(w о-w ¢ _sp)|<<g _{sw o}, при g _s>b ^{2D w} _s=b ²(w ¢ _sn-w ¢ _sp)

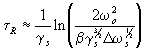(4.5)

Вне области резонанса, где |(w _о-w ¢ _sn)( w о-w ¢ _sp)|>>g _{sw o}, при g _s<D w _s

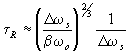(4.6)

Как и в случае отражения от плазмы величина t _R определяется коэффициентом затухания g _s и частотной шириной области полного отражения для случая нормального падания плоских монохроматических волн D w _s.

Результаты, полученные для нормального падения, можно обобщить на случай произвольного угла падения q . Для волны, поляризованной перпендикулярно плоскости падения, в приведенных выше формулах достаточно выполнить следующие замены:

t ± ® t± (zcosq 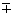xsinq )/c, W p® W p/cosq , a p® a p/cosq , где ось х- направление вдоль границы раздела двух сред. Отметим, что при установлении стационарного отражения угол отражения всегда равен углу падения.

Заключение.

Выполненные расчеты показали, что для всех линейных сред характеристики переднего фронта отраженной волны являются одинаковыми, причем максимальная скорость роста амплитуды отраженной волны определяется величиной 1/W р, т.е. концентрацией электронов cреды. Время установления стационарного отражения на определенной частоте зависит от коэффициента затухания собственных колебаний электронов g и частотной ширины области D w , где в пределе g =0 происходит полное отражение. В случае свободных электронов металлов, когда можно использовать результаты раздела 3, при 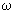_о<<W _p время t _R порядка 1/W р. Для диэлектрика в большинстве случаев время t _R порядка 1/g , за исключением нерезонансного отражения, которое описывается формулой (4.6).

 

ЛИТЕРАТУРА

1. Зоммерфельд А. Оптика.- М.: ИЛ, 1953, с.154.

2.Скроцкая Е.Г., Махлин А.Н., Кашин В.А., Скроцкий Г.В. ЖЭТФ, т.56, в.1, с.220-226 (1969).

3. ЛандауЛ.Д., Лифшиц Е.М. Электродинамика сплошных сред.- М.: Наука, 1982, с.386.