|
|
 |
 |

|
| |
ФУНКЦИЯ ПРОСТРАНСТВЕННОЙ КОГЕРЕНТНОСТИ КАК
ИНФОРМАТИВНЫЙ ПАРАМЕТР ПРИ ИССЛЕДОВАНИИ
ФАЗОВЫХ ОБЪЕКТОВ
Н.Г.Власов, А.Е.Штанько
ВНИИ оптико-физических измерений
119361, г.Москва, Озерная, 46.
Функция взаимной когерентности, описывающая корреляционные свойства волновых полей, является наряду с длиной волны, амплитудой, фазой и поляризацией одним из основных параметров определяющих характеристики этих полей и возможность передачи ими информации как о самих волновых полях, так и об исследуемых объектах и процессах, в которых они применяются как зондирующее излучение.
Функция взаимной когерентности g
12 ( r1 , r 2, t
), как комплексная функция состоит из модуля и аргумента. Аргумент функции взаимной когерентности argg
12 определяется, в частности, разностью фаз интерферирующих волновых полей, и информация, заключающаяся в нем, используется в интерференционных измерениях. Информация, содержащиеся в модуле |g
12| , традиционно используется либо для определения спектрального состава излучения (Фурье-спектроскопия), либо для определения угловых размеров источников излучения (звездный интерферометр Майкельсона, интерферометр Х.Брауна-Твиса).
Анализ литературных данных показывает однако, что за последние два десятилетия появляются отдельные, хотя и немногочисленные публикации [1-4], в которых модуль функции временной либо пространственной когерентности используется как основной информативный параметр в новых, нетрадиционных видах оптико-физических измерений. Малочисленность подобных публикаций объясняется, по нашему мнению, тем, что модуль и аргумент функции взаимной когерентности входит в уравнения, описывающие пространственное распределение интенсивности интерферирующих волновых полей, как сомножители, то есть являются по отношению друг к другу мультипликативной помехой.
В интерференционных измерениях оптические схемы строятся таким образом, что |g
12|=1 и вклад в образование интерференционных полос вносится только arg g
12 . В нашей работе [4] было обращено внимание на тот факт, что при помощи гологра-
фии может быть осуществлена обратная операция, то есть устранен вклад arg g
12, на основе чего был предложен аналог интерференционных измерений, в котором роль эффективной длины волны играла длина когерентности. В настоящей работе описывается аналог теневого метода, основанный на использовании в качестве основного информативного параметра модуля функции пространственной когерентности.
Обратимся к принципиальной оптической схеме, показанной на рис.1. Протяженный квазимонохроматический источник 1 диаметром 2r
(например, вращающееся матовое стекло, освещенное лазерным излучением), освещает дифракционную решетку 2 и непрозрачный экран 3, отсекающий прошедшее мимо излучение. Дифракционная решетка объективом 4 отображается в положение 3¢
таким образом, что используются только плюс-минус первые порядки дифракции, а остальные задерживаются непрозрачным экраном 5. Исследуемый прозрачный фазовый объект 6 вводится в один из первых порядков дифракции, а образованная ими интерференционная картина, являющаяся при отсутствии объекта изображением дифракционной решетки, регистрируется на фотопластинку 7, как голограмма этого объекта.
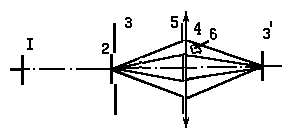
Рис. 1. Принципиальная оптическая схема получения голограммы оптической неоднородности в частично-когерентном излучении
Если в объекте имеются области с градиентом показателя преломления, то освещающее излучение, прошедшее эту область, из-за рефракции смещается в плоскости регистрирующей среды на величину a
l, где a
-угловое смещение прошедшего излучения, l - расстояние от голограммы до объекта. Пусть максимальный угол рефракции a
max будет таким, чтобы максимальное линейное смещение rmax »
a
maxl было равно радиусу области простран-
ственной когерентности Rк, то есть 0 £
r £
Rк. Это всегда можно сделать, имея априорную информацию о максимальных градиентах показателя преломления исследуемого объекта и подбирая угловые размеры освещающего источника, которые собственно и определяют R к [5].
Напомним, что функция g
12( r1, r2, t
) , равная в данном случае g
12( a
l), описывает корреляцию между волновыми полями, интерферирующими в плоскости 3¢
, в зависимости от пространственного сдвига a
l между ними, а
| g
12 | определяет контраст (видность) интерференционных полос, образующих микроструктуру записываемой голограммы. Для тех участков объекта, для которых r=R к, видность равна нулю и голограмма не записывается. Следовательно, при восстановлении изображения они наблюдаются как темные. Участки, для которых r=0, записываются с единичной видностью и наблюдаются как светлые. Для промежуточного случая, когда 0<
r <
Rк восстанавливаются, соответственно, полутоновые изображения.
Дополним данное качественное описание оценкой. Как известно, перекрестный член в уравнении голограммы, описывающий восстановленное волновое поле, U(x,y) ~
g
12, то есть
U(x,y) ~
g
12 (a
l) = | g
12 (a
l) | exp (arg g
12 ) (1) Наблюдение или фотографированию восстановленного изображения, то есть переходу к интенсивности, математически соответствует возведение (1) по модулю в квадрат:
J(x,y) ~
| g
12 (a
l) |2 (2) Таким образом, информация, заключенная в arg g
12 , устраняется, и пространственное распределение интенсивности в восстановленном изображении, зависящее от распределения углов рефракции в исследуемом объекте, определяется конкретным видом функции |g
12 ( a
l)| 2. Вид функции | g
12 | определяется в свою очередь источником освещающего излучения. Так для однородного источника в виде круга радиусом r
:
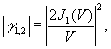 (3) (3)
где 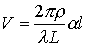 ,J1(V) - функция Бесселя первого рода, ,J1(V) - функция Бесселя первого рода,
l
- длина волны [5].
Строго говоря, уравнение (3) описывает функцию когерентности в плоскости дифракционной решетки 3, однако, если угловые размеры источника излучения меньше, чем угловые размеры апертуры объектива 4 или, другими словами, если область пространственной когерентности в плоскости 3 разрешается оптической системой, то уравнение (3) можно считать справедливым и для плоскости 3¢
.
Функция 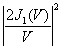 обращается в ноль при значении V=3,83, то есть при обращается в ноль при значении V=3,83, то есть при
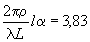 (4) (4)
Вводя обозначения 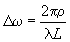 для диапазона пространственных частот и для диапазона пространственных частот и 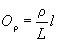 для области теневого размытия точки в плоскости голограммы, можно переписать соотношение (4) в виде: для области теневого размытия точки в плоскости голограммы, можно переписать соотношение (4) в виде:
D
w
R к = 3,83 (5)
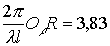 (6) (6)
В физической оптике соотношение неопределенности типа (5) было выведено для диапазона временных частот и времени когерентности, в нашем случае уравнения (5) и (6) связывают соотношением неопределенности чувствительность и разрешение метода. Действительно, увеличение угловых размеров источника излучения увеличивает диапазон пространственных частот, уменьшает Rк и, соответственно увеличивает чувствительность. Одновременно возрастает и область размытия точки на голограмме. Из уравнений (5) и (6) видно также, что соотношение между чувствительностью и разрешением для каждого конкретного случая можно оптимизировать подбором условий, то есть угловых размеров источника, относительного взаиморасположения источника, исследуемого объекта и голограммы. Более подробное рассмотрение показывает, что при приемлемом разрешении ~
10-1 см чувствительность метода равна 10-4 - 10 -5 радиан.
При экспериментальной проверке предложенного метода в качестве исследуемого объекта был выбран участок незасвеченной и отфиксированной фотопластинки, расположенный неподалеку от ее края. На серийных фотопластинках большого формата фотоэмульсия поливается обычно не до самого края, оканчиваясь примерно в 5-10 мм от него, образуя тонкий прозрачный клин с углом ~
10-4 рад. Чтобы избежать внесения дополнительной разности хода, такая фотопластинка вносилась одновременно в обе ветви оптической схемы, а упомянутый клин размещался в объектной ветви. Источником освещающего излучения служил участок вращающегося матового стекла, освещенный неразведенным лучом гелий-неонового лазера ЛГН-222.

Рис. 2. Визуализация фазового объекта по схеме рис. 1.
а - аналог теневого метода светлого поля,
б - аналог теневого метода темного поля.
Изображение, восстановленное полученной голограммой в первом порядке дифракции при освещении ее белым светом, показано на рис.2а. На восстановленном изображении ясно видно, что фазовый объект - клиновидная область границы полива фотоэмульсии - визуализировалась и стала черно-белой в соответствии с теорией, изложенной выше.
Другая голограмма была получена при смещении фотопластинки на величину D
z = 4 мм по оси оптической системы в направлении от объектива. При таком смещении (расфокусировке) происходит взаимное поперечное смещение интерферирующих волновых полей на величину b
D
z , где b
- угол между направлениями их распространения. В результате при b
D
z = Rк контраст интерференционных полос, составляющих микроструктуру голограммы, становится равным нулю и светлое поле заменяется на темное. Если взаимное смещение волновых полей в
результате рефракции на объекте оказывается противоположным по знаку, то оно может скомпенсировать смещение расфокусировки и эти поля придут в плоскость регистрации без сдвига. В результате соответствующие участки объекта окажутся светлыми (рис.2б). Таким образом, расфокусировка оказывается способом смещения центра (начала отсчета) при сохранении диапазона измерения в целом. Указанное обстоятельство позволяет рассчитывать на построение для данного метода аналога метода фазовых шагов [6], и как результат - на увеличение чувствительности на 1-2 порядка и на автоматизацию процесса измерений.
В заключении сравним предложенный метод с классическим теневым (шлирен) методом. В них обоих измеряется пространственное распределение углов рефракции по исследуемому объекту.
В шлирен-методе увеличение чувствительности достигается уменьшением эффективного размера освещающего источника, что сопровождается уменьшением освещенности в плоскости изображения, ограничивающего предельную чувствительность. В рассмотренном методе, напротив, увеличение размеров источника приводит к уменьшению области пространственной когерентности и, соответственно, к увеличению чувствительности. Кроме того, снижаются требования к оптическим элементам, входящим в схему измерения.
ЛИТЕРАТУРА
1. Иванов И.П., Чайковский А.П., Кулейша А.А., ДАН БССР, 1979, т.23, №6, сс.503-506.
2. Abramson N., Appl.Opt., 1983, 22 №2, pp.215-232.
3. Ивакин Е.В., Кишак А.И., Оптика и спектроскопия, 1982, т.25, №1, сс.94-102.
4. Власов Н.Г., Семенов Э.Г., Соколова М.Э. в сб. 17 Всесоюзн.Школы по голографии, Л., 1986, сс.184-197.
5. Борн М., Вольф Э. Основы оптики, М.: Наука, 1970.
6. Reid G.T., Optics and Laser Engineering, 1986, 7, №7, pp.53-68/
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

