|
|
 |
 |

|
| |
РЕШЕНИЕ ФАЗОВОЙ ПРОБЛЕМЫ НА ОСНОВЕ МОДИ-ФИЦИРОВАННЫХ МЕТОДОВ ФАЗОВОГО КОНТРАСТА И
ФАЗОВЫХ ШАГОВ .
Н.Г. Власов, С.Г. Каленков, А.В. Сажин
В методах оптической обработки информации, ставших уже классическими, фильтр пространственных частот, например, комплексный согласованный фильтр Ван-дер Люгта, помещается в Фурье-плоскости оптической системы, на выходе которой получают окончательное, обработанное изображение. Однако в последние годы прослеживается тенденция более перспективного и в то же время более сложного подхода, заключающегося в многошаговой фильтрации исследуемого сигнала - последовательной, как в алгоритме Гершберга-Сэкстона [1], или в одновременной цифровой обработке нескольких независимых результатов фильтрации, как в методе фазовых шагов [2].
В настоящей работе предлагается обобщенный метод фазового контраста, основанный на названном выше принципе и позволяющий, по нашему мнению, достичь заметного прогресса в решении фазовой проблемы.
Напомним, что метод Цернике предназначен для визуализации прозрачных фазовых объектов, комплексная функция амплитудного пропускания которых имеет вид e ij
(x,y) , где описывающая пространственное распределение фазы функция j
(x,y) <
<
1. Визуализация достигается за счет двойного преобразования Фурье объектного волнового поля с фильтром пространственных частот, изменяющим фазу пространственной частоты
w
=0 , либо на + p
/2, либо на - p
/2. Соответственно, визуализированное изображение объекта наблюдается на светлом, либо на темном поле, причем пространственное распределение интенсивности в плоскости изображения прямо пропорционально j
(x,y).
С современной точки зрения метод Цернике представляет собою, хотя и для очень ограниченного частного случая, идеальное решение фазовой проблемы. Рассмотрим существенно более общий случай волнового поля, описываемого комплексной амплитудой a(x,y), в котором j
(x,y) - произвольна, а ограничение накладывается только на соотношение интенсивностей объектного волнового поля и его нулевой пространственной частоты, обсуждаемое ниже.
Следуя каноническому выводу [3] выражения, описывающего обобщенный метод Цернике, запишем исследуемое волновое поле в плоскости изображения в виде:
U(x,y) = [a(x,y) eij
(x,y) - b] + be
eia
(1)
где b - амплитуда нулевой пространственной частоты, а второй сомножитель e
eia
во втором члене правой части (1) описывает действие фильтра пространственных частот. Обозначение координат в плоскостях предметов и изображений совпадают, так как волновые поля, рассматриваемые в фазовой проблеме, как правило достаточно далеко удалены от источника и их спектры пространственных частот, как и для большинства фазовых объектов, представляющих практический интерес, достаточно узки и передаются оптической системой без искажения. Нетрудно показать, что распределение интенсивности I(x,y) в плоскости изображения равно:
I(x,y) = | a(x,y) |2 + b2 + b2e
2 + 2a(x,y)be
cos[j
(x,y) - a
] -
- 2a(x,y)b cos j
(x,y) - 2 b2e
2 cos a
. (2)
Очевидно, что при a( x,y)=1, j
( x,y) <
<
1 и b=1 выражение (2) тождественно выражению, описывающему метод Цернике. Отметим также, что в уравнении (2) модуль нормированной функции взаимной когерентности g
12( x,y, t
) предполагается равным единице. Действительно, t
=0 в силу таутохронных свойств линзы, а для волновых полей, достаточно удаленных от источников, область пространственной когерентности разрешается оптической системой и построение изображения происходит также, как и в случае полностью когерентного освещения. Как и в методе фазовых шагов, получим не одно, а несколько распределений интенсивности в плоскости изображения, считая для упрощения e
=1:
Io(x,y) = | a(x,y) |2 , (3)
I1= b2, (4)
I2(x,y) = | a(x,y) |2 +2 b2 + 2a(x,y)b sin j
(x,y) -
- 2ab(x,y) cos j
(x,y) , (5)
I3(x,y) = | a(x,y) |2 - 2b2 + 2a(x,y)b sin j
(x,y) -
- 2ab(x,y) cos j
(x,y) , (6)
где I o( x,y) - интенсивность нефильтрованного изображения,
I1 - интенсивность нулевой пространственной частоты,
I2(x,y ) и I3( x,y) - интенсивности, соответствующие сдвигу фазы на + p
/2 и на - p
/2 соответственно. Все пространственные распределения Ii( x,y) вводятся в ЭВМ для последующей обработки. Простые алгебраические вычисления приводят к следующему уравне-
нию, определяющему пространственное распределение фазы: 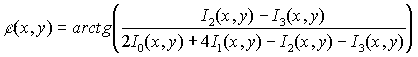 (7) (7)
Как видно из уравнения (7), полученный результат может быть применен как для решения фазовой проблемы, так и для визуализации фазовых объектов с произвольным значением фазы.
Возможно несколько вариантов оптических схем, реализующих рассматриваемый метод. Первый из них является усложненным экспериментом Цернике, заключающемся в последовательном помещении в фокальную плоскость оптической системы необходимых фильтров пространственных частот. Другой - в установке между плоскостями предметов и изображений равноплечного интерферометра Майкельсона, одна ветвь которого, как и в методе фазовых шагов, содержит пьезозеркало для сдвига фаз и пропускает только нулевой порядок, а другая - весь остальной спектр пространственных частот. Общим недостатком этих вариантов является достаточно трудоемкая юстировка оптической схемы. Если спектр пространственных частот достаточно узок, его можно мультиплицировать с помощью дифракционной решетки, помещенной вблизи плоскости предметов и получать по одному из значений I i( x,y) в каждой из мультиплицированных (N+1) копий.
Обсудим теперь допустимые соотношения между интенсивностями нулевого порядка и остального спектра пространственных частот. Практика показывает, что метод фазовых шагов надежно работает вплоть до контраста k изображения (интерференционных полос) равного 0,1. Как известно, k~
Ö
I 1×
Ö
I 2. Таким образом, названное соотношение интенсивностей может изменяться в 102 раз. Так, в уравнении (2) показано ослабление интенсивности нулевой частоты.
Очевидно, также, что точность восстановления фазы рассматриваемым методом совпадает с методом фазовых шагов, положенного вместе с методом Цернике в его основу. По литературным данным, точность метода фазовых шагов, в зависимости от конкретных условий, в долях периода равна 10 -2¸
10 -3 для волновых полей, не зашумленных спекл-эффектом и 10-1¸
10 -2 в его присутствии [4,5].
ЛИТЕРАТУРА
1. Обратные задачи в оптике /под ред.Г.П.Болтса. М.:"Машиностроение", 1984 .
2. Reid G.T. Opt. and Laser Eng., 1986, v.7 , №7, pp.53-68.
3. Борн М., Вольф Э. Основы оптики, М.: Наука, 1973.
4. G.R. Slettemoem, J.C.Wayant, JOSA, 1986, v.3, №3, pp.210-214.
5. R.Dandliker, K.Thalmann, Opt.Eng., 1985, v.24, №5, pp.824-831.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

