|
|
 |
 |

|
| |
МЕТОД ФАЗОВЫХ ШАГОВ
Н.Г.Власов, А.Е.Штанько.
ВНИИ оптико-физических измерений,
103031, Москва, ул.Рождественка, 27
1. Основы метода.
Вероятно, к важнейшим достижениям интерферометрии за последние десятилетия, таким как голографическая и спекл-интерферометрия, скоро можно будет приравнять метод фазовых шагов [1,2] и другие методы. развитые на его основе. Названный метод первоначально был предложен для автоматизации интерференционных измерений на элементной базе современных средств обработки изображений и позволил не только повысить информационную емкость измерений, но, в ряде случаев, и повысить их точность.
Рассмотрим интерференционную картину, образованную наложением двух волн. Распределение интенсивности света I(x,y) в такой картине может быть представлено в виде
I(x,y) = a(x,y) + b(x,y) cosj
(x,y), (1)
где a(x,y) - средняя интенсивность, b(x,y) - амплитуда модуляции интенсивности, j
(x,y) - разность фаз интерферирующих полей.
Выявление функции j
(x,y) из данных, содержащихся в интерференционной картине является целью интерференционных измерений. Изменим фазу одной из интерферирующих волн на величину D
j
. Тогда распределение интенсивности I 1(x,y) в интерференционной картине будет
I = a(x,y) + b(x,y) cos[j
(x,y) + D
j
] , (2)
Проведем эту операцию изменения фазы N раз, добавляя к фазе одной из волн постоянную величину D
j
. Получим соответствующий ряд значений интенсивности I k(k=1,2,...,N). Периодическая функция I(x,y) может быть разложена в ряд Фурье. Коэффициенты разложения Ai(x,y) и Bi(x,y) выражаются формулами
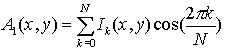 (3) (3)
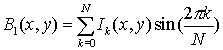 (4) (4)
Искомая величина j
(x,y) равна
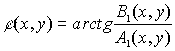 (5) (5)
Формула (5) дает решение задачи в общем виде. Рассмотрим случаи, представляющие наибольший интерес.
Пусть D
j
=120o и регистрируются три распределения интенсивности I1, I 2, I 3, соответствующие фазовым сдвигам +120о, 0 и -120о. В этом случае j
(x,y) вычисляется по формуле [3]
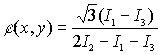 (6) (6)
Такой способ выгоден тем, что требует минимального количества фазовых шагов и, следовательно, минимального объема памяти, необходимого для ввода и обработки интерференционной картины, однако с практической точки зрения неудобен тем, что требует точного контроля величины фазового сдвига между шагами, т.е. точной калибровки фазосдвигающего устройства. Кроме того, отсутствие информации делает метод весьма чувствительным к шумам в оптическом и электронном тракте, что в итоге снижает точность измерений. Для устранения этих недостатков предложены четырех [4], пяти [5] и семишаговые [6] методы.
Первоначально метод фазовых шагов был использован в классической интерферометрии. Ступенчатое изменение фазы опорного волнового поля в заданной последовательности проводилось смещением зеркала, прикрепленного к пьезокерамическому элементу,управляемому компьютером. Процесс измерения полностью автоматизирован и занимает доли секунды (время, необходимое для ввода нескольких телевизионных кадров). Обычно используется формат 512 х 512 точек изображения с 256 градациями яркости. Для каждого пикселя производится вычисление по указанным выше алгоритмам. Полученное в результате распределение фазы имеет разрывы величиной 2p
. Для получения непрерывного распределения фазы необходимо произвести операцию сшивки фазы в точках разрывов. Для этого к каждому элементу массива фазы прибавляется 2p
n, где n - целое число. Число n выбирается для каждого элемента таким образом, чтобы разность между значениями данного и какого-либо уже обработанного соседнего элемента была меньше p
по абсолютной величине. В результате на выходе получается распределение фазы j
(x,y) в виде непрерывной гладкой функции.
В голографической интерферометрии управление фазой интерференционной картины наиболее просто при исследовании объектов в реальном времени, когда ее изменение для восстанавливающего волнового поля осуществляют при помощи подвижного зеркала в опорной ветви интерферометра. В методе двух экспозиций для управления фазой на восстановленном изображении каждую экспозицию производят с отдельным опорным пучком и при восстановлении изменяют фазу в одном из них [7].
Спекл-интерферометрия отличается от голографической в частности тем, что интерференционная картина, составляющая микроструктуру изображения, формируется иногда двумя объектными волновыми полями и для реализации метода фазовых шагов следует изменять, как единое целое, фазу одного из них. Другое отличие - существенное увеличение спекл-шума в телевизионном варианте спекл-интерферометрии. Он вносит существенные помехи при определении фазы и для уменьшения его влияния в процессе обработки интерферограммы на разных стадиях вычисления вводят операции усреднения или фильтрации обрабатываемых данных. Усреднению или фильтрации подвергают разности измеренных интенсивностей до и после нагружения объекта, а также вычисленную фазу. Фильтрацию осуществляют с помощью скользящего фильтрующего окна, размер которого выбирают, исходя из уровня шума. Перед фильтрацией могут проводится также операции исключения дефектных точек, т.е. тех пикселей, в которых по установленным заранее критериям вычисленное значение фазы признано недостоверным. Методика применения метода фазовых шагов в спекл-интерферометрии приведена в [8,9].
Процесс расшифровки муаровых картин во многом сходен с процессом расшифровки интерферограмм. Например, соотношение (1), описывающее интерференционные полосы, в равной степени описывает и распределение интенсивностей в муаровой картине, полученной наложением двух синусоидальных решеток. Отсюда все соотношения, приведенные выше, применимы для муаровых картин, т.е. метод фазовых шагов может успешно использоваться в области муаровых измерений [10, 11, 12]. Для управления фазой муаровых полос в этом случае смещают одну из решеток, дающих муаровую картину, на долю периода (для случая теневого муара меняют величину зазора между решеткой и объектом). В остальном методика регистрации и обработки информации сходна с описанной выше.
Перспективным направлением использования метода фазовых шагов в муаровых измерениях является получение контурных карт рельефа поверхности объекта. Для этого могут быть
использованы решетки, проектируемые на исследуемый объект под углом к направлению наблюдения. TV-камера должна разрешать спроектированную на объект решетку. Из зафиксированного методом фазовых шагов распределения фазы этой решетки по объекту необходимо вычесть распределение фазы, зафиксированное при проектировании той же решетки на плоскость, играющую роль опорной поверхности. Впрочем, опорную поверхность можно "воспроизвести" в компьютере чисто математически, рассчитав предварительно распределение фазы полос на ней, и физически фиксацию второй решетки не проводить.
2. Обсуждение дополнительных возможностей метода.
Использование метода фазовых шагов в классической интерферометрии не только позволяет автоматизировать процесс измерений. Фактически мы имеет дело с новым способом записи волновых полей, являющимся своеобразным аналогом голографической записи. В голографии, правда, записывается как фаза, так и амплитуда волнового поля. Метод фазовых шагов, в описанных в литературе вариантах, регистрирует только фазу волнового поля. Однако в классической интерферометрии амплитуда поля является, как правило, величиной постоянной, поэтому метод фазовых шагов в этом случае в полной мере можно считать методом записи волновых полей. Принципиальное отличие от голографии состоит лишь в том, что в последней записанное волновое поле может быть физически восстановлено (реконструировано), а в методе фазовых шагов оно восстанавливается лишь математически в компьютере. Тем не менее это позволяет воспользоваться основными преимуществами голографии.
Во-первых, открывается возможность использования в конструкции классического интерферометра недостаточно качественных оптических элементов, вносящих фазовые искажения в волновые фронты. Такой интерферометр даже в отсутствии объекта дает на выходе интерферометрическую картину, т.е. не настраивается на "чистое поле". Однако с помощью метода фазовых шагов эта начальная картина распределения фазы может быть записана в памяти компьютера и в дальнейшем будет вычитаться из распределения фазы, получаемого на выходе интерферометра при введении в него исследуемого объекта. Такой интерферометр может быть существенно дешевле обычного, не уступая ему по точности измерений. Можно скомпенсировать и несовершенство голографического интерферометра, устранив, например, интерференционные полосы, образующиеся в результате неточной
установки голограммы на место экспонирования после ее обработки при исследовании в реальном времени.
Во-вторых, для классического интерферометра открывается возможность сравнения различных состояний исследуемого объекта, существующих разновременно. Последовательно записывая распределения фаз, соответствующих двум различным состояниям исследуемого объекта и вычитая их, получаем разностную картину, отображающую происшедшие изменения. Такая методика является аналогом метода двух экспозиций. Особенно большой эффект она может дать при сравнении близких состояний объекта, когда вносимые между экспозициями изменения незначительны и обе интерферограммы почти совпадают. Разность фазовых картин выявляет различия в наглядной форме.
В-третьих, расширяется возможность сравнения различных объектов между собой. В классических интерферограммах такое сравнение производят, помещая сравнимые объекты в два плеча интерферометра. Однако конструктивно не все интерферометры для этого приспособлены. Используя метод фазовых шагов, мы можем последовательно помещать сравниваемые объекты в одно плечо интерферометра и находить затем разность соответствующих фазовых распределений. Если “воспроизводить" предлагаемый для сравнения объект математически в компьютере, то становится возможным сравнивать контролируемый объект с неким идеальным образцовым изделием.
3. Сравнение методов фазовых шагов и фазового контраста.
Напомним, что метод фазового контраста (метод Цернике) применим к фазовым объектам, у которых пространственное распределение фазы j
(x,y)<
<
1. Согласно этому методу, в центре фокальной плоскости объектива. строящего изображение исследуемого объекта, устанавливается фильтр пространственных частот, изменяющий фазу нулевой пространственной частоты объектного волнового поля. Комплексная функция пропускания фильтра описывается выражением D=d eia
, где d - коэффициент ослабления, a
- принимает значение либо +p
/
2 , либо -p
/
2 (методы светлого и темного фазового контраста). Интенсивность в плоскости изображения описывается следующим выражением [13]:
I(x,y) = /c/2[d2+2{1-a cosa
-cos j
(x,y)+d cosj
(x,y)±
a
}], (7)
где /с/ 2 -константа.
В предположении, что j
(x,y) мало, и sin j
(x,y) »
j
(x,y) , предыдущее выражение преобразуется к виду:
I(x,y) = /c/2[d2+2dj
(x,y)]. (8)
Применим к методу Цернике идеологию метода фазовых шагов, то есть получим не одно, а два выражения. соответствующих значениям a
=+p
/
2 и a
=-p
/
2 и описывающихся выражениями типа (8). Вычитая одно из другого, получим:
j
(x,y)= I(x,y)/4 /c/2 d. (9)
Таким образом, замеряя значения I(x,y), мы получаем распределение j
(x,y). Необходимое для нормировки значение 4/с/ 2 d можно получить в дополнительном эксперименте в отсутствии объекта. Из выражения (9) видно проявление и другой характерной черты метода фазовых шагов - увеличение контраста.
4. Обсуждение новых областей применения.
Как известно, под фазовой проблемой в оптике понимается восстановление информации о пространственном распределении фазы волнового поля в одной плоскости пространства по распределению интенсивности, зарегистрированной, вообще говоря, в другой плоскости. Прогресс в решении фазовой проблемы, достигнутый в последние годы, связан, вероятно, со все большим пониманием того факта, что перед регистрацией интенсивности, уничтожающей фазовую информацию, целесообразно произвести сначала некоторое предварительное преобразование волнового поля, позволяющее при переходе к интенсивности облегчить решение задачи. Таким преобразованием может быть, в частности, сам процесс распространения волнового поля и регистрации интенсивности не в одной, а в нескольких плоскостях [14], например в плоскости изображения и в Фурье-плоскости.
Рассмотрим возможный подход к решению фазовой проблемы для волновых полей, в спектре пространственных частот которых заметная часть энергии сосредоточена на нулевой частоте, с привлечением идей фазового контраста и метода фазовых шагов.
Пространственное распределение интенсивности в плоскости изображения будем рассматривать как результат интерференции нулевой пространственной частоты объектного волнового поля с остальным спектром пространственных частот того же объекта. Вводя в память компьютера, в соответствии с уравнением (6) еще два распределения интенсивности и, изменив при этом фазу нулевой частоты, например, на ±
120о, можно согласно (6) найти пространственное распределение фазы в плоскости изображения.
Другой, перспективной с нашей точки зрения областью применения является метрология интерференционных измерений.
Проведенные к настоящему времени исследования точности измерений методом фазовых шагов [15,16] указывают на следующие основные источники погрешности измерений: нестабильность состояния объекта и интерферометра в процессе регистрации фазовых шагов; неточное соблюдение величины фазовых шагов; спекл-шум в изображении объекта (имеет место в голографической и, в особенности, в спекл-интерферометрии);шум, обусловленный наложением перекрестных изображений (в методе двух экспозиций с двумя опорными пучками, разведенными на малый угол); шумы детектора и электронного тракта.
Оценки теоретически достижимой точности измерений, проведенные в работах [15,16], показывают, что каждый из перечисленных источников погрешностей может вносить в измеренную фазу погрешность, имеющую величину от долей до нескольких единиц градусов. В результате для голографической интерферометрии оценка достижимой точности измерений дает величину порядка 1/100 полосы.
Таким образом, чувствительность метода фазовых шагов является промежуточной между обычной и гетеродинной интерферометрией и, следовательно, на его основе можно разработать единые и достаточно близкие методы поверки различных типов классических, голографических и спекл-интерферометров, предназначенных для измерения пространственного распределения физических величин, выражающихся через пространственное распределение изменения оптического пути объектного волнового поля. Названные методы поверки, в свою очередь могут быть аттестованы на основе гетеродинного метода, что позволяет расчитывать на создание отсутствующей в данный момент единой поверочной схемы для интерференционных методов названного типа.
ЛИТЕРАТУРА
1. Reid G.T., Autimatic Fringe Pattern Analysis: A Rewiew, Op tics and Lasers Engineering, v.7, №7, 1986, pp.53-68.
2. Ryszard T., Review of methods for automatic analysis of fringers in hologram interferometry. SPIE, v.816 Interferometric Metrology, 1987, pp.140-148.
3. Rolinson P.W., Williams D.C., Digital phase stepping speackle interferometry, Optics communications, v.57, №1, 1986, pp.26-30.
4. Creath K., Phase-shifting speackle interferometry, Applied Optics, v.24, №18, 1985, pp.3035-3057.
5. Hariharan P., Oreb B.F., Eiju T., Digital Phase-shifting interferomet ry: a simple error compensating phase calculation algorithm, Applied Optics, v.26, №13, 1987, pp/2504-2505.
6. Larkin K.G., Oreb B.F., New seven-sample symmetrical phase-shifting algorithm, Proc. SPIE №1755, pp.2-11.
7. Thalmann R., Dandlicker R., High re solution video processing for holographic interferometry applied to contouring and measuring deformations, Proc. SPIE, №492 (1985), pp.299-306.
8. Zheng W. Phase Stepping DSPI and its application, Proc. SPIE, v.1821, 1992, pp.46-51.
9. Owner-Petersen M., D igital speackle pattern shearing interferometry: limitations and prospects, Applied Optics, v.30, №19, 1991, pp.2730-2738.
10. Yoshizawa T., Tomisama T., Opt.Engineering, v.32, №7, 1993, p.1668.
11. Williams D.C. at al., Digital phase-step interferometry: a simlified approach, Optics and Laser Technology, v.23, №3, 1991, pp.147-150.
12. Rosvold G.O., Fast measurement of phase using a PC-base frame graffer and phase stepping technique, Appl. Opt., v.29, №2, 1990, pp.237-241.
13. Борн М., Вольф Э., Основы оптики, изд. "Наука" М., 1973.
14. Кузнецова Т.И., ТрудыФИАН 1991, т.212 "Оптика и лазеры", с.38-57.
15. Dandliker R., Thalmann R., Heterodyne and quasi-heterodyne holographic interferometry, Opt.Engineering, v.24, №5, 1985, pp.824-831.
16. Slettemoen G.A., M aximal fraction of accepteble measurements in phase-shifting speakle interferometry: a theoretical study, Journ. Opt. Sos. Am. A, v.3, №2, 1986, pp.210-214.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

