|
|
 |
 |

|
| |
МАСШТАБНОЕ ВОССТАНОВЛЕНИЕ НЕСТАЦИОНАРНЫХ ИЗОБРАЖЕНИЙ В ДИНАМИЧЕСКОЙ ЭХО-ГОЛОГРАФИИ
С.М.Захаров, Э.А.Маныкин
Рассматриваются пространственно-временные масштабные преобразования нестационарных изображений , осуществляемые сигналами типа модифицированного стимулированного фотонного эха при возбуждении трехуровневых резонансных систем импульсами свата со сферическим волновым фронтом.
В настоящее время получили значительное развитие методы динамической голографии. основанные на восстановлении нестационарных оптических полей. Один из возможных способов осуществления голографической записи изменяющихся во времени оптических сигналов состоит в использовании нестационарной опорной волны с линейным изменением частоты по сечению /1-3/. Причем при восстановлении .одномерного изображения пучком, аналогичным опорному, но с иной скоростью изменения частоты, возможно масштабное преобразование во времени.
Другой способ основан на явлении фотонного эха (ФЭ). Благодаря свойству фазовой памяти при записи эхо-голограммы допускается разнесенность во времени объектной и опорной волн, а чувствительность резонансной среды к спектральному составу падающего света проявляется в записи и восстановлении нестационарных объектных сцен. Именно эти особенности были продемонстрированы в цикле работ по пространственно-временной голографии в высокоселективных фотохромных средах на основе фотохимического выжигания провалов /4-8/. В итоге при восстановлении нестационарных объектных сцен оказывается возможным как прямой, так и обратный ход времени.
Новые особенности в записи и восстановлении нестационарных изображений появляются при использовании многоуровневых резонансных сред. Как известно, воспроизведение временной формы возбуждающих импульсов света в этих условиях сопровождается характерным
масштабным преобразованием, зависящим от конкретных механизмов неоднородного уширения резонансных уровней анергии /9/. Поясним это на примере сигнала модифицированного стимулированного фотонного эха (МСФЭ), возникающего в трехуровневой резонансной среде при возбуждении тремя импульсами света. МСФЭ является аналогом обычного стимулированного ФЭ, однако, когерентность, запасенная в среде после действия двух возбуждающих импульсов но резонансной переходу "а®
в" частоте W
в разности населенностей уровней "а" и "в", а вместе с тем и в населенности уровня "в", реализуется третьим импульсом на частоте w
, резонансной переходу "в®
с". На этой же частоте возникает когерентный отклик в виде сигнала МСФЭ.
В теории ФЭ для поляризации можно получить следующей выражение /9/:
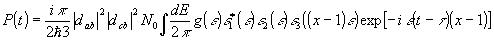 (1) (1)
где dab, dcb - матричные элементы дипольных моментов резонансных переходов, N0 - концентрация резонансных атомов, t
= t
1 + t
2 + t
3/(х - 1) соответствует времени возникновения сигнала МСФЭ, t
1 и t
2 интервалы между возбуждающими импульсами света, функция q(e
), зависящая от расстройки e
, описывает форму неоднородно-уширенной линии, коэффициент х = (w
ca - w
ºca)/(w
ba - w
ºba) определяется механизмом неоднородного уширения спектральных переходов "с®
а'' и "в®
а", а функции e
a
(в) являются Фурье-образами медленных огибающих импульсов возбуждения:
e
a
= ò
dtEa
(t)exp(ie
t), a
= 1,2,3 (2)
В частных случаях, когда спектральная ширина функций e
1(e
), e
2(e
) или e
3((x¾
1)e
) оказывается наименьшей в выражении (1), поляризация P(t) будет пропорциональна E*1((x-1)(t
-t)), либо E2((x-1)(t-t
)), либо Е(t - t
). Таким образом,
сигнал МСФЭ воспроизводит временную форму возбуждающего импульса либо в реальном, либо в измененном масштабе времени.
В настоящем сообщении мы хотим обратить внимание на то, что подобные масштабные преобразования возможны при воспроизведении пространственной структуры нестационарных изображений и использовании импульсов света со сферическим волновым фронтом.
Пусть сферическая световая волна, имеющая центр кривизны волнового фронта в точке Z = -R1, 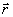 = 0 освещает плоский информационный транспарант Т с амплитудным пропусканием T( = 0 освещает плоский информационный транспарант Т с амплитудным пропусканием T(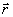 ,t), находящийся в плоскости Z = 0. Резонансная среда малой протяженности помещается на расстоянии L от транспаранта. и играет роль динамической фазовой голограммы. Поле вблизи голограммы будет иметь вид: ,t), находящийся в плоскости Z = 0. Резонансная среда малой протяженности помещается на расстоянии L от транспаранта. и играет роль динамической фазовой голограммы. Поле вблизи голограммы будет иметь вид:
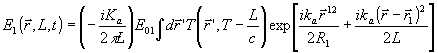 (3) (3)
где k a - волновое число. Спустя промежуток времени t
1 и t
2 резонансная среда подвергается воздействию двух других импульсов, также имеющих сферический волновом фронт с радиусом кривизны Ra
и центром кривизны в точке Z = L - Ra
, 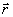 = =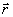 0a
. 0a
.
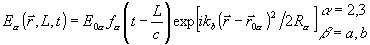 (4) (4)
где волновое число ka для третьего импульса света, а вместе с тем и для сигнала МСФЭ, отлично от ka, а функции ƒa
(t) описывают временную форму импульсов возбуждения.
Приведем окончательное решение электродинамической задачи, учитывающей квантовые свойства резонансной среды. В параксиальном приближении для амплитуды эхо-отклика вместе с произвольной координатой Z и плоскостью наблюдения 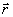 a
можно получить следующее выражение: a
можно получить следующее выражение:
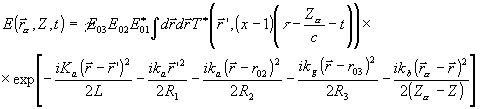 (5) (5)
где g
- некоторый коэффициент зависящий от свойств резонансной среды и параметров возбуждающих импульсов света. Из выражения (5) следует условие возникновения четких изображений, т.е. плоскость сформированного сигналом ФЭ изображения должна отстоять на расстоянии L' от резонансной среды
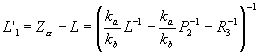 (6) (6)
При выполнении данного условия интегрирование в исходном выражении (5) выполняется до конца и для амплитуды электрического поля и интенсивности эхо-отклика получим
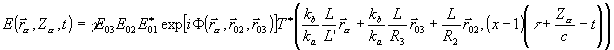
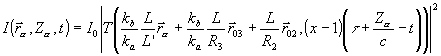 (7) (7)
Za
= L + L'
где Ф (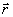 a
, a
,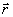 02, 02,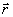 03) - некоторая фазовая функция, а g
' - константа, выражаемая через g
. 03) - некоторая фазовая функция, а g
' - константа, выражаемая через g
.
Из последнего выражение (7) следует, что сигнал МСФЭ формирует в плоскости 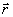 a
с координатой Za
нестационарное изображение, ход времени в котором является зеркально-обращенным, а само изображение - пространственно-подобное с характерным масштабным множителем М: a
с координатой Za
нестационарное изображение, ход времени в котором является зеркально-обращенным, а само изображение - пространственно-подобное с характерным масштабным множителем М:
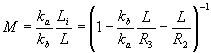 (8) (8)
Если информационными свойствами обладает второй возбуждающий импульс света, то условие возникновения четкого изображения, а также выражения для интенсивности и коэффициента масштабных преобразований будут иметь вид:
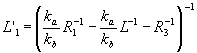 (9) (9)
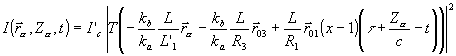 (10) (10)
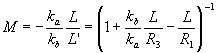 (11) (11)
Наконец, запись исходного изображения может осуществить третий импульс света, тогда
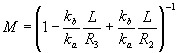 (12) (12)
Из полученных выражений для коэффициента масштабных преобразований (8), (11), (12) следует, что восстановленные изображения носят пространственно-подобный характер, причем при возбуждении резонансной среды импульсами света с плоским волновым фронтом (Ri = ¥
) изображения, сформированные сигналами: ФЭ, остаются масштабно-неизменными, т.е. М = 1. В общем случае характер преобразования исходного изображения /сжатие или растяжение/ зависит от величины |
M|
, при |
М|
> 1 будет наблюдаться растяжение, а при |
M|
< 1 - сжатие.
Таким образом, резонансная среда выполняет двойную роль: - во-первых, роль спектрально-селективной голограммы, позволяя восстанавливать нестационарные изображения, во-вторых, роль некоторой оптической системы, параметры которой определяются радиусом кривизны волнового фронта и частотами возбуждения импульсов света.
Литература
1. Зубов В.А., Крайский А.В., Кузнецова Т.И. // Письма в ЖЭТФ, т.13, с.443, 1983.
2. Боркова В.Н., Зубов В.А., Крайский А.В. // Труды ФИАН, 1982. т.131, с.68; а также // Актуальные проблемы спектроскопии. М.: 1985, с.132.
3. Крайский А.В. Препринт ФИАН № 222. М.: 1968.
4. Саари П.М., Каарли Р.К., Ребане А.К. // Квант.электрон. 1985, т.12, с.672.
5. Саари П.М. Труды ин-та физики АН Эстонии. 1986, т.59, с.157.
6. Saari P., Kaarli R., Rebane A. // SPIE proceed. Seminar. 1937, v.673, р.53.
7. Rebane K.K., Saari P.M. // Physica Scripta. 1987, v.T19B, p.604.
8. Rebane K.K., Kaarli R.K., Rebane A.K., Saari P.M. In: Laser Optics of Condensed Matter. N.V., Plenum. 1933.
9. Захаров С.М., Маныкин Э.А. // ЖЭТФ, 1966, т.91, с.1209; 1989, т.95. с.1587.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

