|
|
 |
 |

|
| |
СПЕКТРАЛЬНО-УГЛОВАЯ ДИАГНОСТИКА ФОТОЭМУЛЬСИОННЫХ ГОЛОГРАФИЧЕСКИХ РЕШЕТОК
В.В.Крылов, Ю.П.Удоев
Рассмотрены результаты экспериментального исследования углового и спектрального распределений дифракционной эффективности фотоэмульсионных голографических решеток пропускающего типа с пространственными частотами 1100-2400 лин/мм, приготовленных на пластинках ВРЛ, ЛОИ-2, ПЭ-2, ПФГ-03 при различны экспозициях и режимах химической обработки. С позиций теории Когельника интерпретированы особенности полученных спектральных распределений, выявлены различия между измеренными угловыми зависимостями и ожидаемыми в рамках идеальной модели фазовой решетки, обычно используемой при теоретическом анализе. На основе известных теоретических расчетов намечены критерии диагностики решеток.
Экспериментальному исследованию дифракционных свойств фотоэмульсионных голографических решеток (ФГР) посвящено много работ /1-5/. Однако в большинстве случаев исследования проведаны на фиксированной длине волны (обычно 0,63 мкм) и ограничены изучением влияния вида фотоматериала и технологии его обработки на экспозиционную характеристики. Нами было проведено комплексное исследование фазовых ФГР припускающего типа, включающее измерения спектрального распределения дифракционной эффективности (ДЭ) и угловых зависимостей ДЭ при различных условиях получения решеток. Исследование было предпринято с целью изменения возможности применения промышленных фотопластинок ЛОИ-2-633, ПЭ-2, ПФГ-03, ВРЛ для создания высокоэффективных голографических элементов, рассчитанных на роботу совместно с полупроводниковыми лазерами, однако, полученные данные представляют и более общий интерес для физики фотоэмульсионных регистрирующих сред.
ФГР записывались на длине волны 0,63 мкм на установке
СИН-1 в сходящихся пучках по симметричной схеме либо с делением фронта, либо с делением амплитуды волны при соотношении интенсивностей световых пучков - 1:1, имеющих S-поляризацию. Для уменьшения влияния неидентичности химической обработки и свойств фотоэмульсионных слоев на каждой пластинке записывалось несколько решеток при различных экспозициях. Пространственные частоты решеток находились в диапазоне 1100-2400 лин/мм. Химическая обработка проводилась в основно тремя способами:
А - метод Чанга-Виника (Ч-В) /6/ после проявления в Д-19;
Б - обычное отбеливание после проявления в растворе Д-19 и фиксирования;
В - отбеливание после проявления в концентрированных растворах ГП-2 и фиксирования.
Во всех случаях отбеливание производилось в растворе R-10, содержащем К J. Характерные времена обработки: проявление в Д-19 - 5 мин, проявление в ГП-2 - 12 мин, отбеливание - 5-8 мин, фиксирование - 5 мин. ФГР, полученные путем отбеливания, дополнительно обрабатывались в осветляющем растворе сульфита натрия.
Спектральное распределение ДЭ измерялось в диапазоне 0,5-1,0 мкм в коллимированном пучке за выходной щелью монохроматора УМ-2 при падении волны под углом Брэгга. Угловые зависимости ДЭ автоматически регистрировались на длине волны 0,63 мкм с помощью установки, включающий усилитель постоянного тока, электронный потенциометр, генератор пилообразного напряжении и вращающийся столик, на котором были укреплены решетка и датчик угловых меток. Все измерения проводились при S-поляризации падающей волны.
Наиболее характерный вид спектральных распределений ДЭ для решеток с пространственной частотой 1680 лин/мм, записанных на пластинках ЛОИ-2, приведен на рис.1, где по оси ординат отложена величина относительной дифракционной эффективности h
(ОДЭ) первого порядка, определяющаяся в общем случае по соотношению:
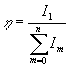 (1) (1)
где n - общее число дифракционных порядков в проходящем свете, I1 и Im - интенсивности пучков первого и m-ого порядков соответственно. При обработке по методу Ч-В достигнуты высокие (~96%) значения ОДЭ в районе l
= 0,63 мкм, однако, с увеличением l
величина ОДЭ монотонно уменьшается (рис.1а). При отбеливании получены зависимости h
(l
) как такого же (кривые 1 на рис.1б и 1в), так и другого типа, характеризующиеся наличием максимума при l
= 0,8 мкм, причем величина ОДЭ в этом максимуме также является высокой (94-96%) (кривые 2 на рис.1б и 1в).
Общий характер приведенных зависимостей h
(l
) можно объяснить на основе из лестного /7/ выражения для ОДЭ чисто фазовой пропускающей решетки:
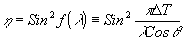 (2) (2)
где ƒ - "сила" решетки, D
- амплитуда синусоидальной фазовой модуляции, Т - толщина решетки, l
- рабочая длина волны в вакууме, q
- внутренний угол Брэгга. Расчетные кривые h
(l
) на рис.1 получены путем привязки к экспериментальным значениям при l
~ 0,63 мкм (кривая 2 на рис.1б и кривые рис.1в) и l
~ 0,78 мкм (кривые рис.1а и кривая 1 на рис.1б). При расчете учитывалось изменение внутреннего угла Брэгга с изменением l
, а величина D
считалась постоянной. Из (2) следует, что если при некоторой длине волны l
* величина ƒ(l
*) < p
/2 то при l
> l
* ОДЭ будет уменьшаться с ростом l
, а с уменьшением l
- увеличиваться. При ƒ(l
*)>p
/2 поведение h
(l
) должно быть противоположно предыдущему. Как видно из рис.1, экспериментально могут быть получены зависимости h
(l
) обоих типов. Отсюда следует, что область спада h
на экспозиционных характеристиках ФГР в некоторых случаях может быть связана с достижением ƒ = p
/2 в максимуме этой характеристики. Надежным критерием перевала через ƒ = p
/2 является спектральное поведение именно ОДЭ, а не абсолютной ДЭ, определяемой по отношению к интенсивности падающей волны.
Расхождения между расчетными и экспериментальными зависимостями h
(l
) частично можно приписать влиянию дисперсии D
, немонохроматичности падающей волны и недостаточной коллимированности
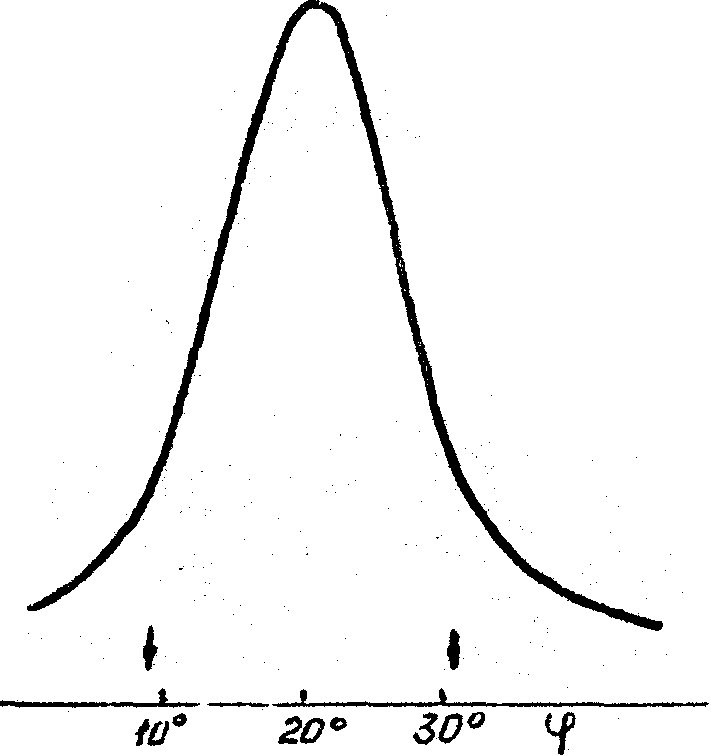
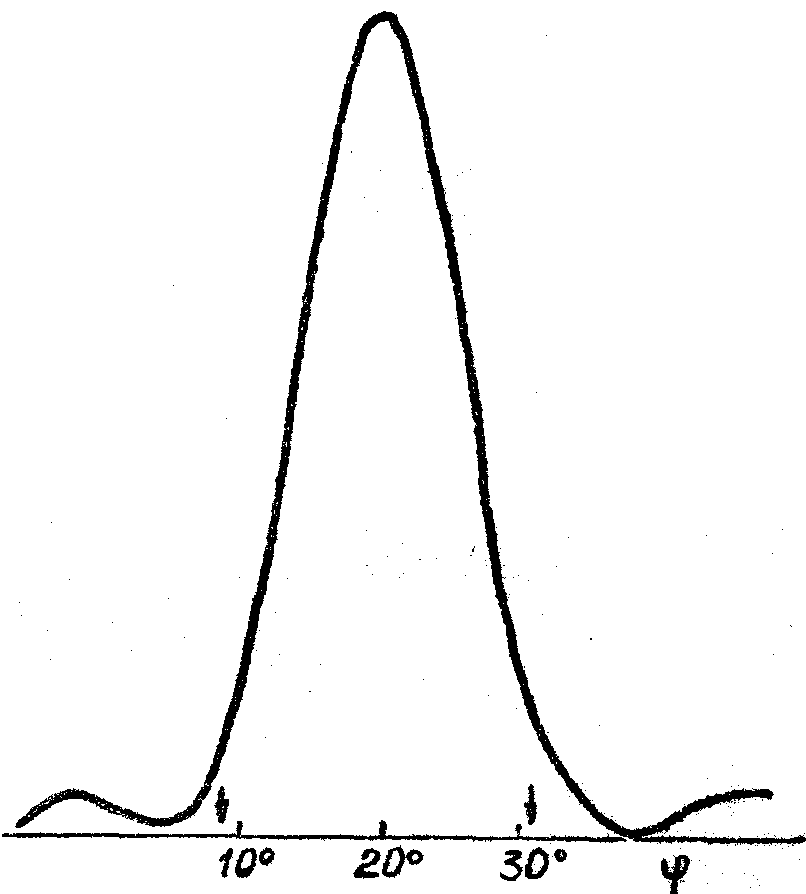
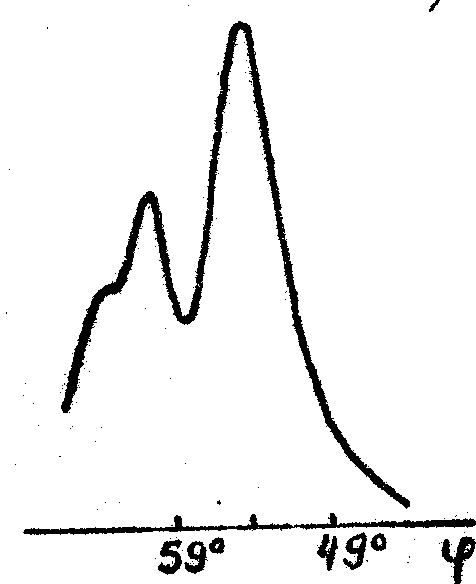
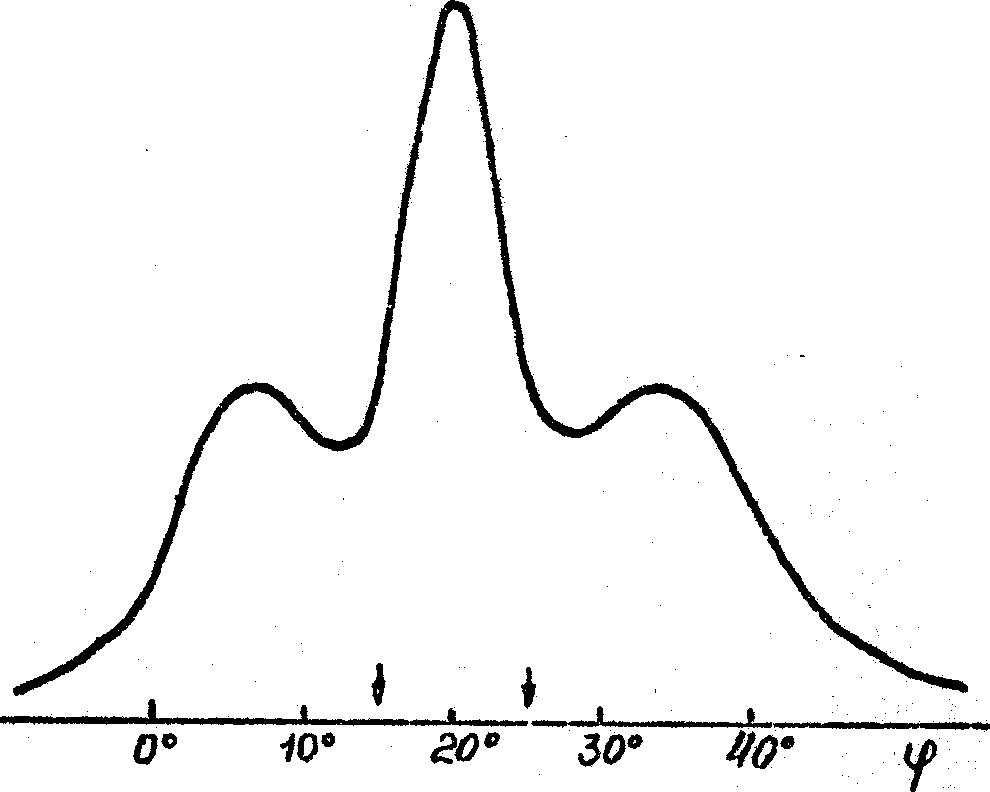
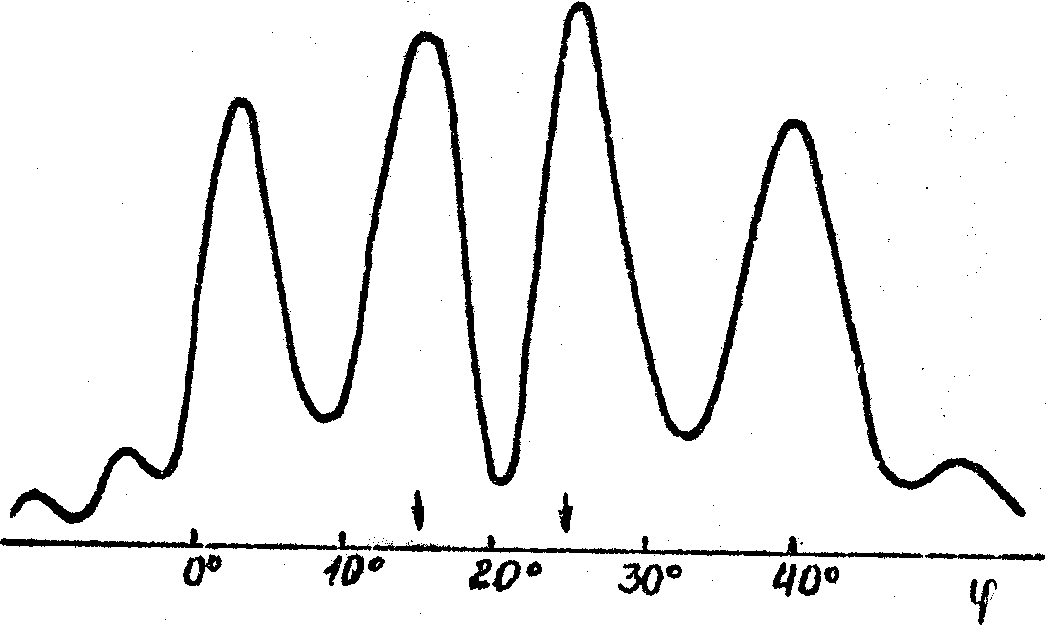
освещающего пучка. Однако в некоторых случаях эти расхождения могут быть связаны прежде всего с отличием реальных периодических структур от идеальной модели, обычно предполагаемой при теоретическом анализе. В пользу этого заключения свидетельствуют очевидные различия между реальными угловыми спектрами (рис.2-6) и известной идеальной угловой зависимостью ДЭ, для которой характерно наличие центрального брэгговского пика и ряда симметрично расположенных боковых максимумов, относительная высота которых зависит от величины ОДЭ /7-9/. Примеры экспериментальных угловых зависимостей ДЭ такого типа приведены на рис.2б и рис.4б. На этих и других рисунках стрелками показано положение первых минимумов ДЭ, рассчитанных по теории Когельника /7/; по оси абсцисс везде отложена величина угла падения относительно нормали к поверхности эмульсионного слоя. Как видно из рис.2-6 реальные спектры имеют аномалии трех типов: (1) - отсутствие боковых максимумов (рис.2а и За); (2) -наличие группы боковых максимумов, расположенных только на одном из склонов основного пика (рис.4а и 5), (3) - наличие провала ДЭ при углах падения, близких к ожидаемому положению центра брэгговского пика (рис.6). Аномалии первого типа получены ними при записи решеток на пластинках всех типов, аномалии второго типа - на пластинках ЛОИ-2, аномалии, третьего типа - в основном на пластинках ВРЛ, обработанных по методу Ч-В, причем провал ДЭ появлялся лишь при достаточно больших экспозициях и при записи решеток на достаточно "свежих" эмульсиях.
Исходя из теоретических результатов работ /10,11/ можно заключить, что отсутствие боковых максимумов связано с уменьшением величины D
вдоль нормали к поверхности эмульсионного слоя, Этот эффект, частично может быть объяснен оптическим поглощением и эмульсии на стадии записи решеток и с практической точки зрения является полезным при таких применениях ФГР, в которых необходима хорошая угловая селекция анализируемых сигналов. Учитывая результаты расчетов /11/, аномалии второго типа можно объяснить искривлением плоскостей решетки. Вероятной причиной такого искривления могут быть остаточные напряжения эмульсионного слоя /11,12/. Значительное влияние этого эффекта на вид
угловых зависимостей ДЭ иллюстрируется рис.7, на котором приведены результаты проведенного нами расчета h
(j
) для простой модельной структуры, показанной на вставке к рисунку. Расчет выполнен путем применения известных /7/ выражений для амплитуд дифрагированной и проходящей волны последовательно к двум решеткам при учете интерференции двух пар волн. возникающих во второй (наклонной) решетке. Результаты модельного расиста позволили также объяснить наблюдаемую асимметрию кривых h
(j
) при изменении знаке j
(рис.5б,в). Таким образом, исследование угловых зависимостей ДЭ может быть проведено методом контроля остаточных напряжений эмульсионного слоя при отработке технологии производства пластинок или непосредственно перед их применением.
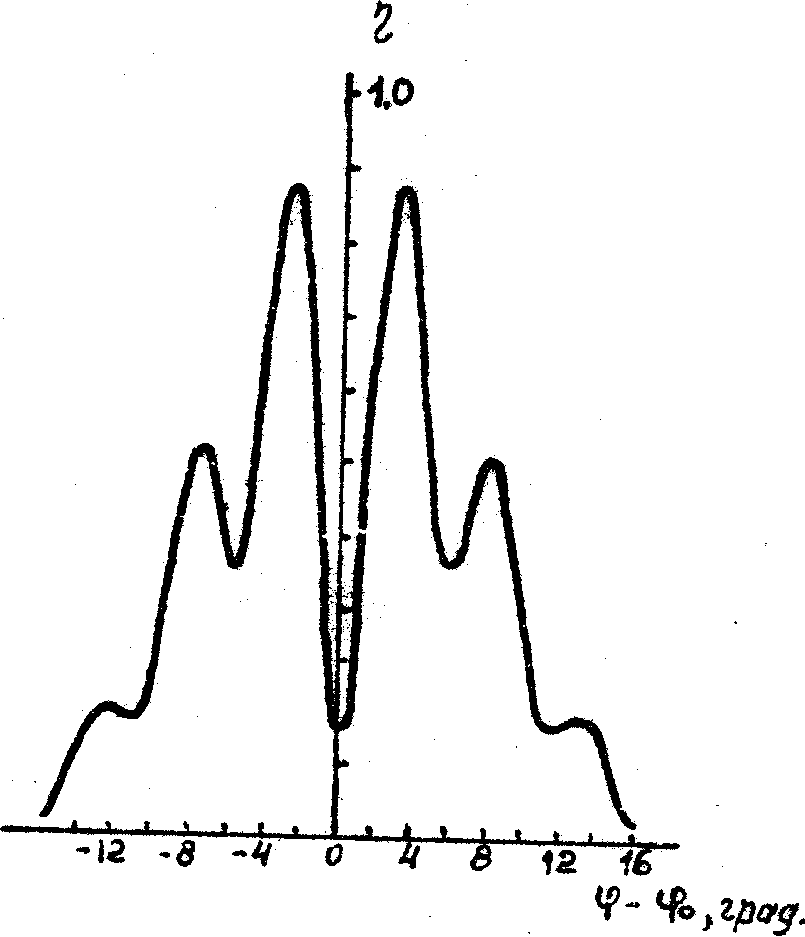
Аномалии третьего типа на кривых h
(j
) являются качественно новым эффектом, обусловленным, по-видимому .образованием двух решеток, смененных относительно друг друга. В пользу такого заключения свидетельствуют результаты проведенных нами расчетов h
(j
) для структуры, состоящей из двух решеток с различными значениями Т, D
, величины фазового сдвига y
. Наиболее хорошее качественное соответствие эволюции расчетных и экспериментальных кривых h
(j
) с ростом экспозиции получено для случая y
= p
и толщинах решеток Т1 и Т2, соответственно, 4 и 14 мкм. В качестве примера на рис.8 показаны кривые h
(j
), рассчитанные при l
= 0,9 мкм, l
= 0,63 мкм. Возможной физической причиной образования двух решеток при обработке фотоматериала по методу Ч-В является одновременная реализация поверхностных (например, крэки) и объемных механизмов модуляции показателя преломления, аналогичных наблюдавшимся при записи решеток на бихромированной желатине /13-15/. Как непосредственно следует из расчетных данных, образование двух решеток может существенно ограничивать предельно достижимую величину ДЭ.
Таким образом, полученные экспериментальные данные и результата более ранних исследований (в частности - амплитудно-фазовых структур /16,17/) показывают, что измерения спектрального и углового распределения ДЭ являются весьма полезным инструментом для технологического контроля состояния эмульсионного слоя и диагностики параметров и структуры голографических решеток.

Рис.1. Расчетные (сплошные линии) и экспериментальные зависимости ОДЭ от длины волны для решеток, полученных методом Чанга-Виника (а), путем отбеливания после проявления в Д-19 (б) и путем отбеливания после проявления в растворах ГП-2 (в). Время экспонирования, мин.: 1 - 4.6, 2 - 6 (а), 1 - 2, 2 – 10 (б), 1 - 4, .2 - 1 (в).
а) б)
Рис.2. Угловая зависимость ДЭ для решеток с пространственной частотой ~ 1100 лин/им, записанных: на пластинках ПЭ-2 и обработанных по способу А. Время экспонирования, с.: а - 100, б - 280.
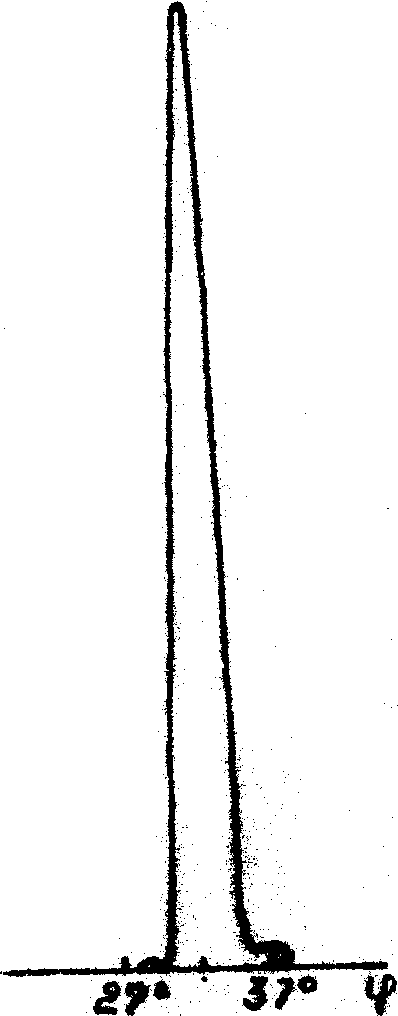 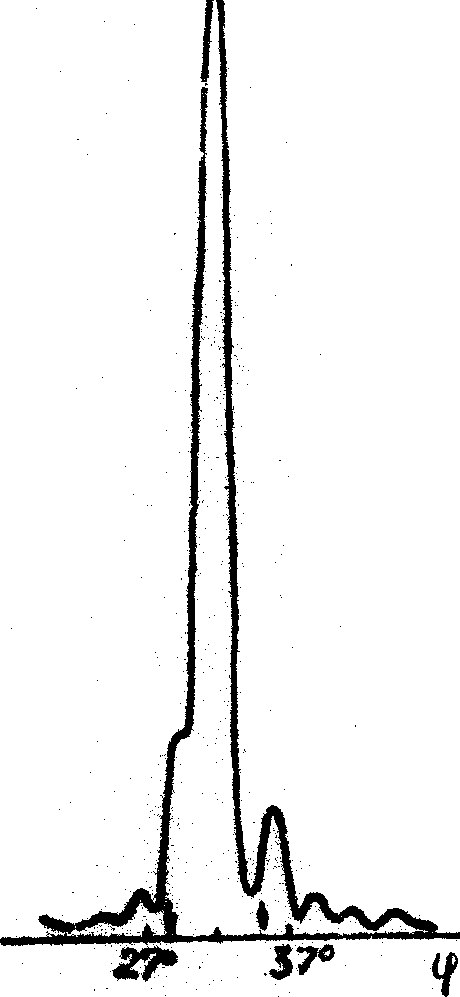
а) б)
Рис.3. Угловая зависимость ДЭ для решеток с пространственной частотой ~ 1700 лин/мм, записанных на пластинках ЛОИ-2 и обработанных по способу А (а) и по способу Б с дополнительной дегидратацией в изопропаноле (б).
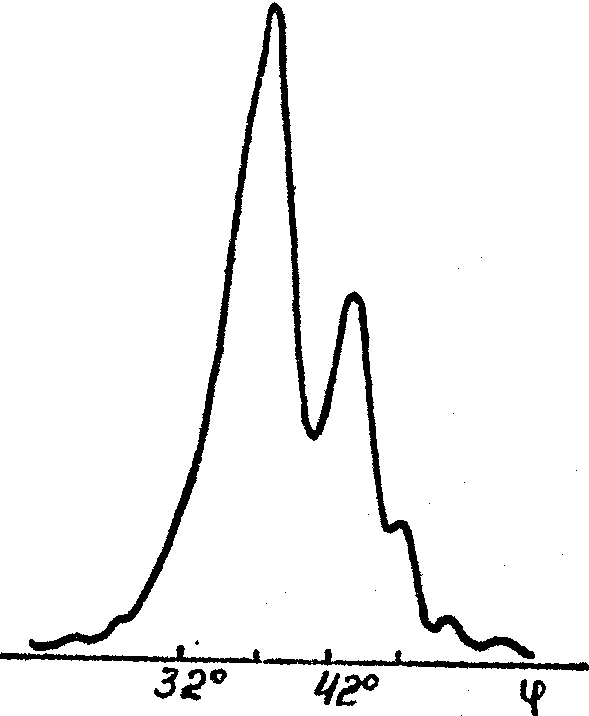 
а) б)
Рис.4. Угловая зависимость ДЭ для решеток с пространственной частотой ~ 1700 лин/мм, записанных на пластинках ЛОИ-2 и обработанные по способу В. Концентрации растворов и времена экспонирования: а - 10%, 8 мин, б - 34%, 4 мин.
 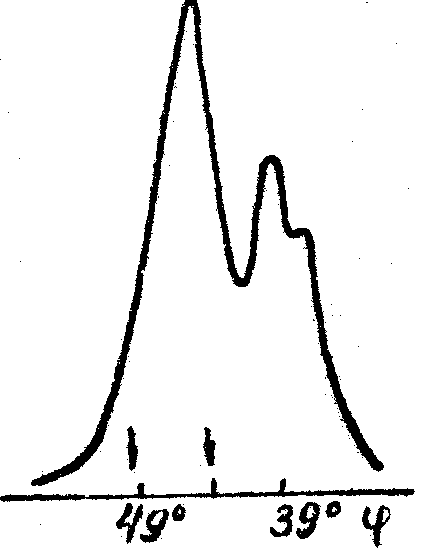 
а) б) в)
Рис.5. Угловая зависимость ДЭ для решеток с пространственной чистотой ~ 2400 лин/мм, записанных на пластинках ЛОИ-2 и обработанных по способу Б (а) и также с дополнительной дегидратацией В изопропаноле (б,в). б и в - освещение одной и той же решетки слева и справа от нормали.
а)
б)
Рис.6.
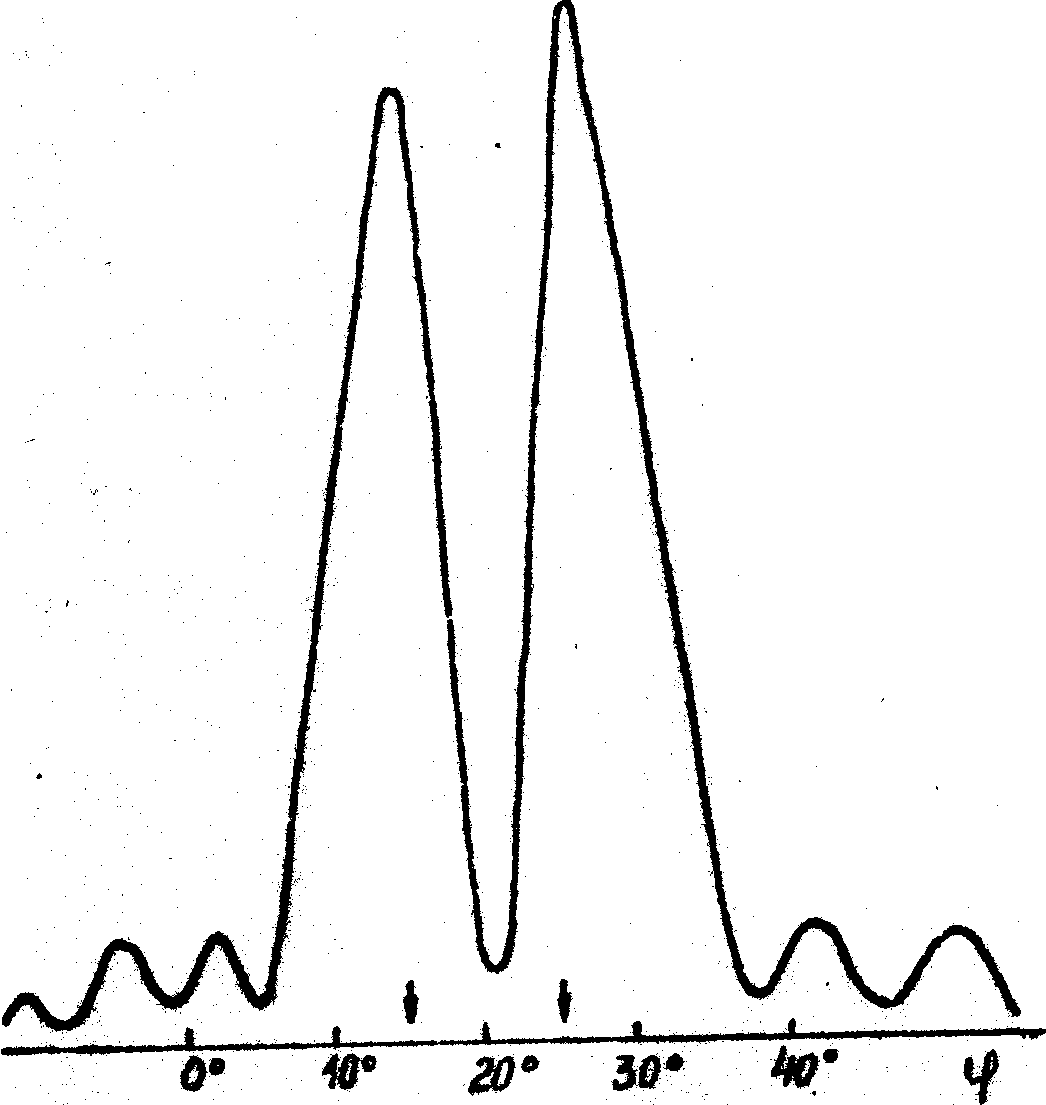
в)
Рис.6. Угловая зависимость ДЭ для решеток с пространственной частотой ~ 1100 лин/мм, записанных на пластинках ВРЛ и обработанных по способу А. Время экспонирования, с.: а - 2, б - 5, в - 13.
а) б)
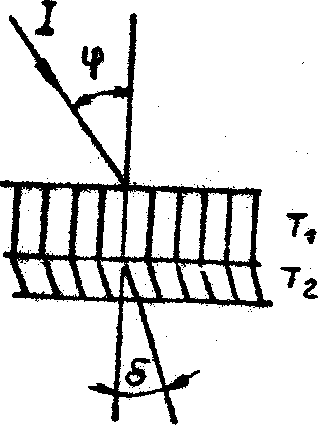
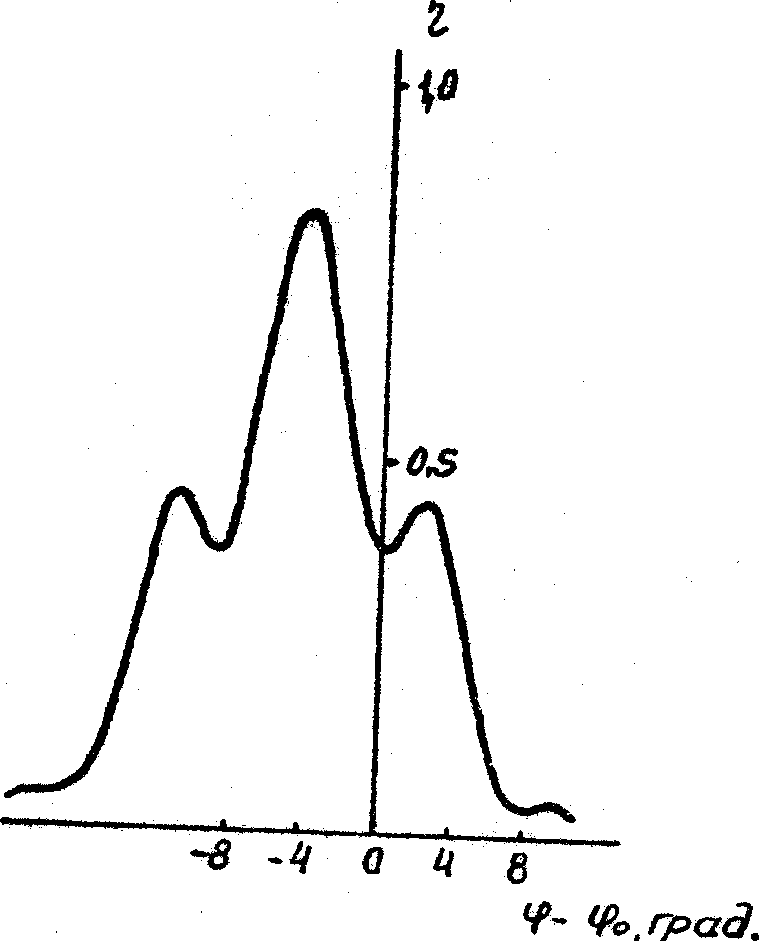
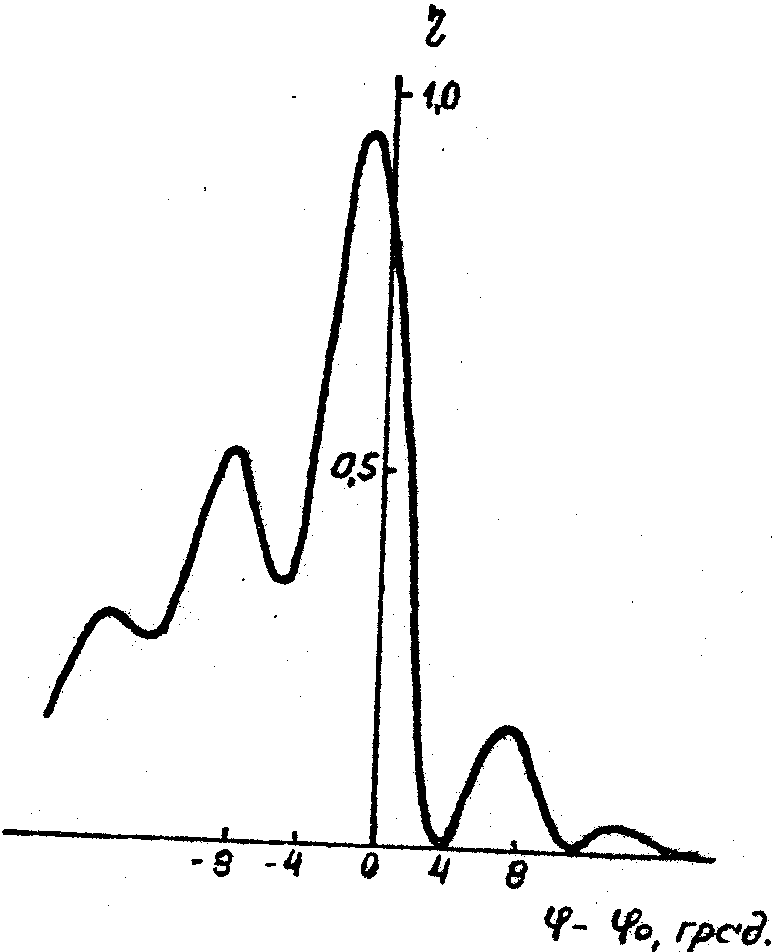
Рис.7. Расчетная угловая зависимость ДЭ для сложной структуры, содержащей прямую и наклонную решётки. Параметры решеток:
а – Т 1 = 9мкм, Т2 = 3 мкм, ƒ1 = ƒ 2 = p
/4, L
= 0,8 мкм, d
= 4º
б – Т 1 = Т2 = 6 мкм, ƒ1 = ƒ 2 = p
/4, L
= 0,8 мкм, d
= 6º
а) б)
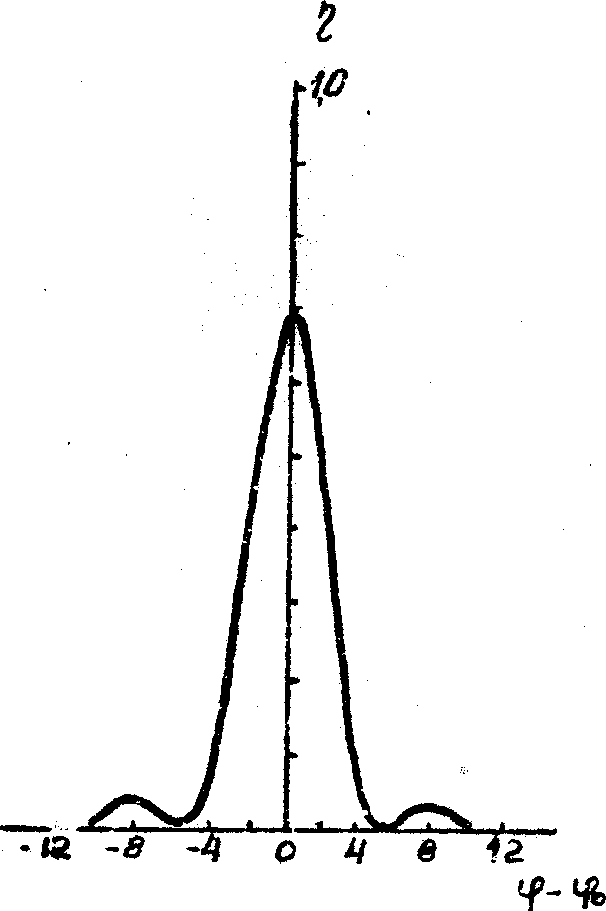
Рис.8.
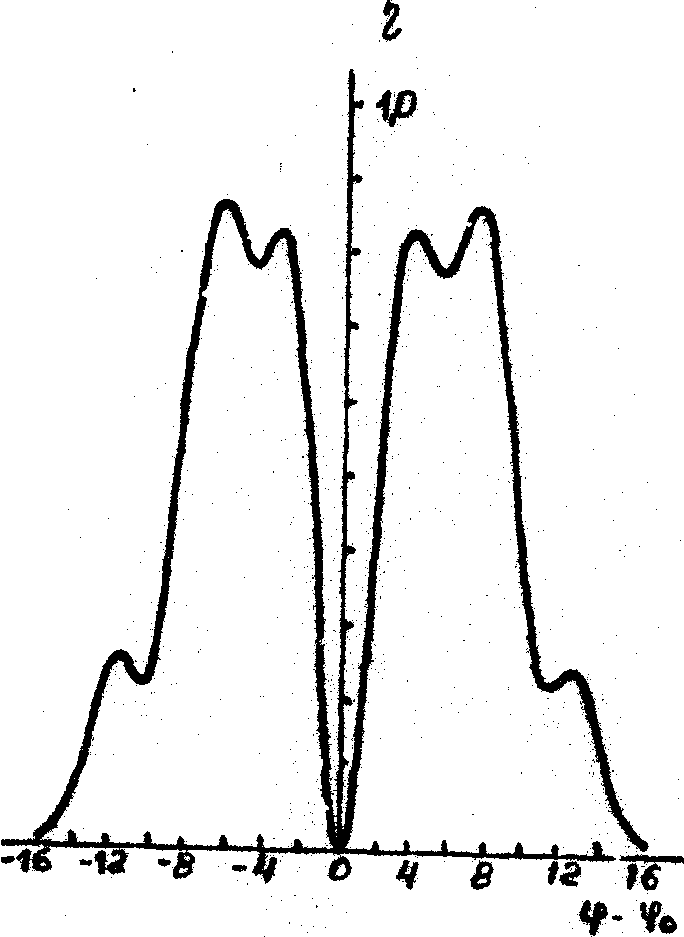
Рис.8. Расчетная угловая зависимость ДЭ для сложной структуры, содержащей две прямые решетки с периодом О,9 мкм, сдвинутые относительно друг друга на полпериода.
Параметры решеток: а – ƒ 1 = 0, ƒ 2 = 5 p
/16
б – ƒ 1 = p
/4, ƒ 2 = 3 p
/8
в – ƒ 1 = p
/2, ƒ 2 = p
/2.
Литература
1. Кольер Р., Беркхарт К., Лин Л. Оптическая голография. И., 1973.
2. Регистрирующие среды для голографии. Л., 1975.
3. Кириллов Н.И. Высокоразрешающие фотоматериалы для голографии и процессы их обработки. М., 1979.
4. Syms R.R.A., Solymar L. Planar volume phase holograms formed in bleached photographic emulsions // Appl.Opt. 1933, v.22, N 10, р.1479-1496.
5. Стаселько Д.И., Чураев Л.Л. Исследование фазовых характеристик регистрирующих сред для голографии // Оптика и спектр. 1984, т.57, в.4, с.677-683.
6. Chang B.J., Winick К. Silver-halide gelatin holograms // SPIE, 1980, v.215. р.172-177.
7. Kogelnik H, Coupled wave theory for thick hologram gratings // Bell Syst. Techn. J. 1969, v.48, N 9, p.2909-2947.
8. Burckhardt С.В. Diffraction of a plane wave at a sinusoidally atratified dielectric grating // JOSA. 1966, v.56, N 11, p.1502-1509.
9. Крупицкий Э.И., Чернов Б.К. Строгая теория объемных голографических решеток и перспективы ее развития. - // Материалы 6 Всесоюзн. школы по голографии. Л., 1974, с,46-80.
10. Leith S.N. Kozma A., Upatnieks J., Marks J., Masney M. Holographic data storage in three-dimensional media // Appl. Opt. 1966, v.5, N 8, p.1303-1311.
11. Kubota T. The bending of inter ference fringes Inside a hologram // Optica Actica. 1979, v.26, N 6, р.731-743.
12. Friesem A.A., Walker J.L. Experimental investigation of some anomalies in photographic plates // Appl.Opt. 1969,v.8, N 7, р.1504-1506.
13. Curran R.K., Shankoff T.A. The mechanism of hologram formation in dichromated gelatin // Appl.Opt. 1970, v.9, N 7, p.1651-1657.
14. Chang В.J., Leonard C.D. Dichromated gelatin for the fabrication of holographic optical elements // Appl.Opt. 1979, v.18, N 14, p.2407-2417.
15. Баженов В.Ю., Бурыкин Н.М., Васнецов М.В., Волков С.В., Соснин М.С., Тараненко Б.Б. Исследование процессов образования объемных фазовых голограмм в слоях бихромированной желатины // УФЖ. 1982, т.27, № 1, с 30-36.
16. Алексеев-Попов А.В., Гевелюк С.А. Определение вкладов амплитудной и фазовой модуляции в дифракционную эффективность объемных голограмм. - // Оптическая голография. Л. 1983, с.14-24.
17. Алексеев-Попов А.В., Гевелюк С.А. Влияние сдвига между амплитудной и фазовой компонентами голограмм на ее угловую селективность. - // Тезисы докл. 5 Всесоюз.конф. по голографии. Рига, 1985, с.65-60.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

