Media-security

МЕТОДЫ СОЗДАНИЯ ДВУХКООРДИНАТНЫХ ГОЛОГРАФИЧЕСКИХ ДИФРАКЦИОННЫХ РЕШЕТОК

Б.Г.Турухано, Н.Турухано

Рассмотрены методы создания двухкоординатных голографических дифракционных решеток с помощью двух-, трех- и четырехлучевого интерферометра. Приведены аналитические выражения распределения интенсивности интерференционных полос в выходной апертуре этих интерферометров. Представлены экспериментальные данные.

1. Введение

Осуществление двухкоординатных измерений перемещений традиционно производится двумя датчиками перемещений, механически связанными между собой. Поэтому точность измерений перемещений на двухкоординатном приборе определяется точностью изготовления механических узлов, осуществляющих двухкоординатное перемещение, и обычно в процессе измерений не контролируется. Уникальные возможности голографии позволяют создать двухкоординатные дифракционные решетки, которые при использовании в системах измерений перемещение автоматически связывают измерения по двум координатам.

Одним из методов создания участка интерференционного поля с ортогональным распределением интерференционных полос является метод, использующий трехлучевой и четырехлучевой интерферометры.

2. Анализ

Рассмотрим случай четырехлучевого интерферометра. На выходе такого интерферометра образуются четыре коллимированных пучка когерентного света, центральные лучи которых находятся в ортогональных плоскостях и образуют угол q с осью OZ. Проекции волновых векторов в четырехлучевом интерферометре заданной конфигурации можно записать в виде:

₁ = -_1x - _1z

₂ = -_2y - _2z

₃ = -_3x - _3z

₄ = -_4y - _4z

(1)

Проекции волновых векторов можно выразить через длину вектора и угол падения q :

K_1x = K_2y = K_3x = K_4y = (2p /l )Sinq

K_1z = K_2z = K_3z = K_4z = (2p /l )Cosq

(2)

Волновые фронты пучков в четырехлучевом интерферометре запишутся следующим образом:

S₁ = exp[i(-K_1xx – K_1zz)]

S₂ = exp[i(-K_2yy – K_2zz)]

S₃ = exp[i(K_3xx – K_3zz)]

S₄ = exp[i(K_4yy – K_4zz)]

(3)

Интенсивность интерференционной картины можно представить как квадрат модуля суммы амплитуд пучков:

I = | S₁ + S₂ + S₃ + S_4|² = S²₁ + S²₂ + S²₃ + S²₄ + S^*₁S₂ + S₁S^*₂ + S^*₁S₃ +

+ S₁S^*₃ + S^*₁S₄ + S₁S^*₄ + S^*₂S₃ + S₂S^*₃ + S^*₂S₄ + S₂S^*₄ + S^*₃S₄ + S₃S^*₄

(4)

Принимая амплитуды волн за единицу и комбинируя попарно интерференционные члены с одинаковыми индексами в выражении (4), а также учитывая значения, S₁, S₂, S₃ и S₄ из выражения (3) и проекции волновых векторов из (2), получим, к примеру, для пятой и шестой

пар выражение:

S^*₁S₂ + S₁S^*₂ = exp[-i(-K_1xx – K_1zz)]·exp[i(-K_2yy – K_2zz)] +

+ exp[-i(K_1xx – K_1zz)]·exp[-i(-K_2yy – K_2zz)] =

= exp[i(K_1xx – K_2yy)] + exp[-i(-K_1xx – K_2yy)] =

= 2Cos[2p Sinq ·(x - y)/l ]

(5)

Преобразовывая (1), как показано выше, получим распределение интенсивности интерференционных полос в выходной плоскости четырехлучевого интерферометра в виде:

I(x,y) = 4 + 2{2Cos[2p u (x - y)] + 2Cos[2p u (x + y)] +

+ Cos(2p 2u x) + Cos(2p 2u y)}

(6)

где u = 2Sinq /l - пространственная частота интерференционных полос. Выражение (6) описывает две системы ортогональных интерференционных полос. Причем первая система ортогональных полос определяется первыми двумя членами в фигурных скобках, имеет пространственную частоту u и наклонена под углом ± 45º к оси ОХ. Вторая система ортогональных полос отвечает третьему и четвертому членам, имеет удвоенную пространственную частоту 2u и каждая система полос параллельна осям ОY и ОХ, соответственно. Аналогично можно получить распределение интенсивности интерференционных полос с выходной плоскости ХОY трехлучевого интерферометра в виде:

I(x,y) = 3 + 2{2Cos[2p u (x - y)] + 2Cos[2p u (x + y)] + Cos(2p 2u y)} (7)

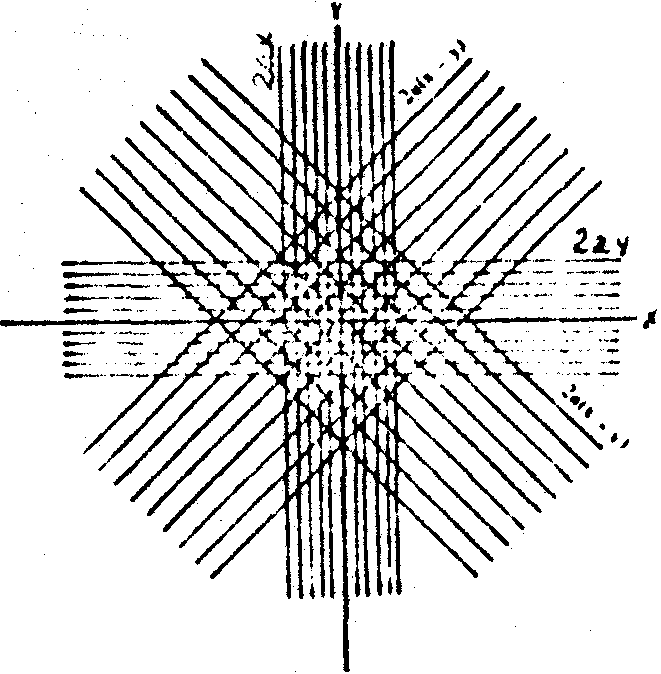
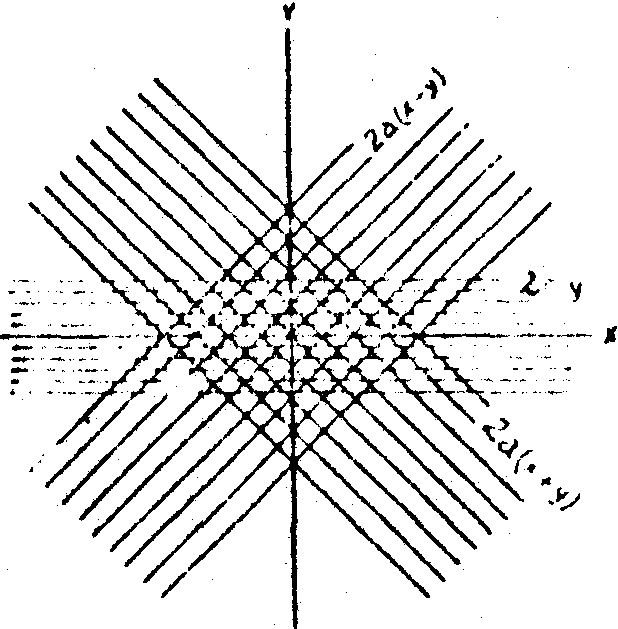
Распределение интерференционных полос четырехлучевого и трехлучевого интерферометров дано на рис.1 (а и б).

Другим методом создания двухкоординатных голографических решеток может служить метод с использованием двухлучевого интерферометра с двухкратной записью. Для получения двухкоординатного распределения линий перед второй записью решетка поворачивается на угол 90°.

При первой регистрации волны S₁ и S₂ можно записать как

S₁ = exp[i(-K_1xx – K_1zz)]

S₂ = exp[i(K_2xx – K_2zz)]

После поворота решетки на 90° вокруг оси ОZ волны S₃ и S₄ примут вид:

S₃ = exp[i(-K_3yy – K_3zz)]

S₄ = exp[i(K_4yy – K_4zz)]

(8)

Интенсивности интерференционных полей на первом и втором этапе записи голографической решетки можно описать выражениями:

I₁ = | S₁ + S_2|² = S²₁ + S²₂ + S^*₁S₂ + S₁S^*₂

I₂ = | S₃ + S_4| = S²₃ + S²₄ + S^*₃S₄ + S₃S^*₄

(9)

В случае линейной регистрации суммарная интенсивность волн, зарегистрированная фотопластинкой, дается выражением:

I(x,y) = I₁ + I₂ = 4 + 2[2Cos(2p 2u x) + + Cos(2p 2u y)] (10)

Таким образом, в результате двухкратной экспозиции на фотопластинке зарегистрируются две системы интерференционных линий, ортогональные друг другу.

а)

б)

Рис.1. Распределение интерференционных полос в выходной плоскости а) четырехлучевого, б) трехлучевого интерферометров.

3. Эксперимент

Картина дифракции фокусированного лазерного пуча на голографической дифракционной решетке, структура интерференционных линий, которая описывается уравнениями (5) и (7), приведены на рис.2 (а и б). Ассиметрия в распределении интенсивности дифракционных порядков (рис.2-б) обуславливается отсутствием в выражении (7) одного из членов с двойной частотой 2u .

Конструкция четырехлучевого интерферометра для записи голографической решетки с ортогональным распределением линий показана на рис.3. При изготовлении голографической решетки, дифракционная картина которой дана на рис.2а, призматические элементы интерферометра заменялись на линейные голографические дифракционные решетки.

На рис.4 приведена картина дифракции лазерного пучка на голографической дифракционной решетке, полученной в результате двухкратной экспозиции, структура интерференционных полос которой описывается уравнением (10).

Картину дифракции можно объяснить, используя принцип суперпозиции в оптике, следующим образом: лазерный пучок испытывает двойную дифракцию, вначале на первой системе интерференционных линий голографической решетки, давая лучи в три порядка +1, 0, -1; эти лучи затем дифрагируют на ортогональной системе интерференционных линий решетки, создавая на выходе следующие порядки дифракции:

(+1, +1)

(0, +1)

(-1, +1)

(11)

(+1, 0)

(0, 0)

(-1, 0)

(+1, -1)

(0, -1)

(-1, -1)

Продолжая рассуждения, можно объяснить картины дифракции, полученные от голографических решеток, записанных в трех- и четырех- лучевом интерферометрах. Отметим, что углы дифракции лучей будут определяться пространственными частотами соответствующих систем интерференционных линий голографической решетки, а ряд порядков дифракции будут накладываться друг на друга в силу кратности пространственных частот. К примеру, порядок (+1, 0, -1) накладывается на порядок (0, +1, +1), порядок (0, 0, -1) - на порядок

а)

б)

Рис.2. Картина дифракции фокусированного лазерного пучка на голографической решетке, записанной в а) четыркхлучевом и б) трехлучевом интерферометрах.

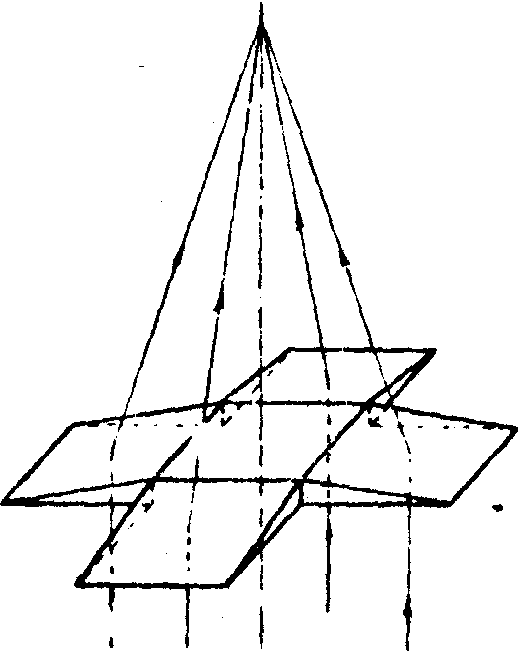
Рис.3. Конструкция четырехлучевого интерферометра и ход осевых лучей.

Рис.4. Картина дифракции фокусированного лазерного пучка на двухкоординатной голографической решетке.

(-1, +1, +1) и т.д. На рис.5 приведены порядки дифракции, образованные в результате дифракции фокусированного лазерного пучка на голографической решетке, линейно записанной в трехлучевом интерферометре. Появление дополнительных порядков на экспериментальной картине дифракции рис.2б в сравнении с картиной, полученной аналитическим путем - рис.5, обусловлено нелинейностью записи голографической решетки.

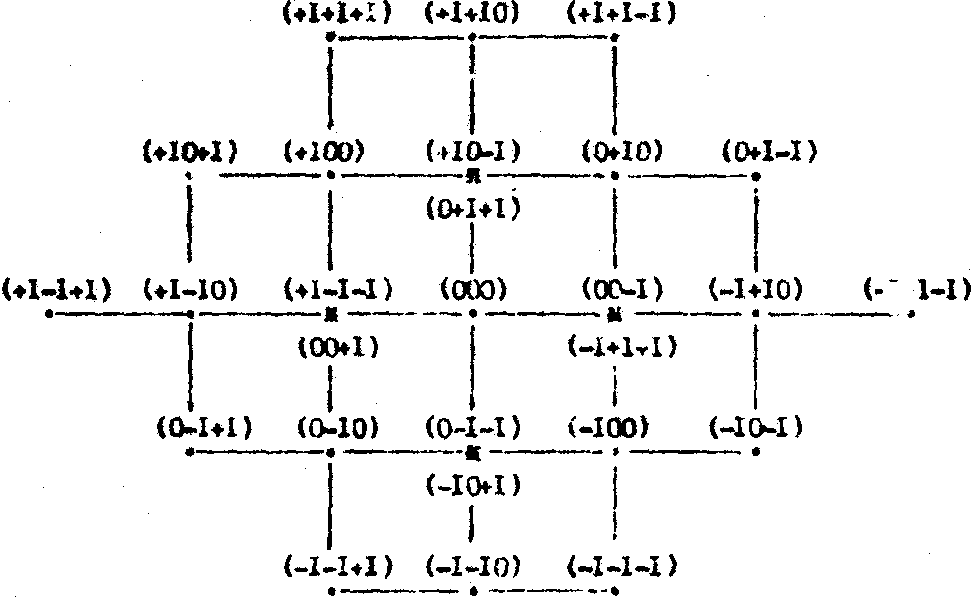
Рис.5. Порядки дифракции, образованные голографической решеткой, записанной в трехлучевом интерферометре. Крестиком обозначены места, где порядки накладываются.

4. Выводы

Рассмотрены три метода записи двухкоординатных решеток, каждая из которых может служить в качестве измерительного элемента в двухкоординатных фотоэлектрических преобразователях линейных перемещений. Записанные решетки с частотой 250 лин/мм позволяют

получить при простой интерполяции шага на 4 разрешение преобразователя, равное 1 мкм. Но представляет трудности записать двухкоординатные голографические решетки с периодом 1 мкм и тем самым получить при той же интерполяции разрешение, равное 0,25 мкм.

Литература

1. Добырн В.В., Турухано Б.Г. Турухано Н. "Метрические свойства комбинации интерференционного поля и синусоидальной голографической дифракционной решетки". Опт. и спектроскопия., 1971, т.30, вып.3 c.550-555.

2. Турухано Б.Г., Турухано Н. "Голографические системы для измерения линейных перемещений и фазовых сдвигов", // Материалы III Всесоюзной школы по голографии, Л.: ЛИЯФ, 1971, с.213-233.