|
|
 |
 |

|
| |
ЛОКАЛИЗАЦИЯ ИНТЕРФЕРЕНЦИОННЫХ ПОЛОС В СПЕКЛ-ИНТЕРФЕРОМЕТРИИ *)
И.С.Клименко, В.П.Рябухо, Б.В.Федулеев
Рассматривается явление локализации полос в двухэкспозиционной спекл-интерферометрии. Показано, что, как и в голографической интерферометрии, локализованный характер полос обусловлен взаимным смещением идентичных спекл-полей, образующихся при рассеянии когерентного света на двухэкспозиционной спеклограмме. Предлагается использовать в спекл-интерферометрии расшифровку интерферограмм "методом счета полос", широко применяемым в голографической интерферометрии. Проводится сравнительный анализ чувствительностей методов.
Введение
В классической интерферометрии явление локализации интерференционных полос, т.е. наличие пространственной области с наилучший видностыо полос, наблюдается в интерферометрах с протяженными тепловыми источниками, дающими излучение с существенно ограниченной пространственной и временной когерентностью /1/.
При использовании пространственно когерентного (одномодового) лазерного излучения область локализации интерференционной картины ограничивается разностью хода интерферирующих пучков, т.о. значением временной когерентности /1,2/. В голографической интерферометрии разность хода интерферирующих волн обычно значительно меньше длины когерентности, поэтому явление локализации полос имеет место в основном при изучении объектов с диффузно-отражающими поверхностями или при использовании диффузоров в исследованиях фазовых объектов. В этом случае рассеянное объектом световое поле - спекл-поле - имеет ограниченную область пространственной корреляции и его можно рассматривать как аналог светового поля, создаваемого протяженным тепловым источником с ограниченной областью пространственной когерентности /3,4/.
*) Настоящая лекция была прочитана на XVI Школе по голографии, 1985 г.
Явление локализации полос в голографической интерферометрии представляет собой один из наиболее интересных и в то же время неочевидные вопросов. Интерес к этой проблеме не ослабевает до настоящего времени и вызван тем, что изучение закономерности локализации полос, с одной стороны, позволяет глубже понять физические механизмы образования интерференционных картин в голографической интерферометрии, а с другой стороны, дает возможность извлекать дополнительную измерительную информацию ' об изменениях, происшедших с объектом. Выявление и анализ аналогий в эффектах локализации полос в голографической интерферометрии и в классической интерферометрии с использованием тепловых источников позволяют устанавливать общие закономерности образования интерференционных картин.
При исследовании явления локализации полос в голографической интерферометрии использовались различные подходы (см., например, библиографию в /5/), что, несмотря на многочисленные экспериментальные проверки, приводило зачастую к противоречивым результатам: для одних и тех же типов смещений объекта различными авторами определялись разные области локализации интерференционных полос /6/. В настоящее время наиболее часто для определения положения поверхности локализации полос, т.е. дня нахождения геометрического места точек, где видность полос равна единице, используется так называемая геометрическая теория локализации /5/. Следует однако отметить, что эта теория не имеет достаточно наглядного физического содержания и в ее рамках не достаточно полно описываются распределение видности. полос в области локализации, а также явление осцилляции видности полос.
Б связи с этим в последнее время нашел распространение новый подход к объяснению явления локализации полос в голографической интерферометрии диффузно отражающих объектов, обусловленный развитием оптика спеклов. Согласно этому подходу /7-12/, локализация полос имеет место в областях пространства, где объектные спекл-поля, соответствующие исходному и смещенному состояниям объекта, претерпели относительное смещение,
не превышающее размеров спеклов *), которые следует рассматривать как область пространственной корреляции диффузно когерентного поля. Максимальная видность полос наблюдается там, где спеклы не изменили своего пространственного положения. Например, для наклона объекта - это плоскость изображения объекта вблизи оси наклона, для поступательного смещения при плоской освещающей волне - это задняя фокальная плоскость линзы (плоскость Фурье-образа), для вращательного сдвига - линия в пространстве. Отметим также, что если регистрировать спеклограмму в области локализации голографической интерферограммы какого-либо типа смещения объекта, то спекл-интерферограммы не чувствительны к этому типу смещений, поскольку в плоскости регистрации отсутствует соответствующее смещение спеклов. Осциллирующий характер видности голографических интерферограмм в рамках указанного подхода обусловлен /11,12/ суперпозицией различных максимумов амплитуды идентичных спеклов, имеющих, подобно импульсному отклику, тонкую амплитудно-фазовую структуру.
Наряду с голографической интерферометрией в последние годы успешно развивается еще одно направление в интерференционных измерениях - спекл-интерферометрия. Хотя этот метод появился и совершенствовался во многом под влиянием плодотворных приемов и идей голографической интерферометрии, тем не менее, сначала сложилось мнение, что эти методы существенно отличаются друг от друга. Существовала даже такая точка зрения, согласно которой будто бы с помощью голографической интерферометрии измеряют смещения, тогда как методом спекл-интерферометрии - деформации и напряжения /14/. Некоторые авторы (см., например, /15/) относят спекл-интерферометрии двойной экспозиции или, как часто называют этот метод, спекл-фотографию, к неинтерференционным методам, а образование полос объясняют по аналогии с муаровым эффектом. Муаровая аналогия при объяснении механизма образования
*) По существу аналогичный подход рассматривался в /2,13/ для голографической интерферометрии фазовых объектов с диффузором.
полос и спекл-интерферометрии в настоящее время является весьма распространенной /16/. В ряде случаев она, безусловно, помогает при интерпретации сигнала измерительной информации в спекл-интерферометрии, однако, она не вскрывает истинных физических процессов формирования полос в этом методе, которые являются интерференционными и аналогичными, процессам образования полос в голографической интерферометрии. В частности, именно муаровой аналогии, на наш взгляд, обязало своим появлением распространенное утверждение, что полосы спекл-интерферограммы всегда локализованы на изображении объекта /16-19/. Ниже будет показано, что это утверждение на самом деле является неверным: в двухэкспозиционной спекл-интерферометрии поверхность локализации полос никогда не совпадает с плоскостью изображения. В отдельных случаях могут наблюдаться полосы, локализованные в ограниченных участках изображения.
Следует подчеркнуть, что исследование локализации полос в спекл-интерферометрии имеет такие не важные методическое и прикладное значения, как и в голографической интерферометрии.
1. Образование полос в двухэкспозиционной спекл-интерферометрии
В спекл-интерферометрии двойной экспозиции информация об изменениях, происшедших с объектом, записывается в виде взаимного смещения элементов спекл-структур, регистрируемых на фотопластине. Считывается эта информация путем освещения двухэкспозиционной спеклограммы когерентной волной, которая пространственно модулируется обеими зарегистрированными спекл-структурами (рис.1). В результате за спеклограммой образуются два идентичных спекл-поля, т.е. два поля, имеющих идентичный фазовый микрорельеф волновых фронтов. Эти световые поля отличаются взаимным пространственным сдвигом идентичных элементов, который носит чисто поперечный характер в силу того, что на спеклограммы при любом смещении объекта регистрируются только поперечине смещения спеклов. При реализации одноапертурного метода записи спеклограммы минимально регистрируемое смещение спекл-структур равно размеру спекла /20/ - только в этом случае
световые волны, рассеянные на спеклограмме, приобретают фазовый сдвиг, необходимый для образования одной интерференционной полосы.
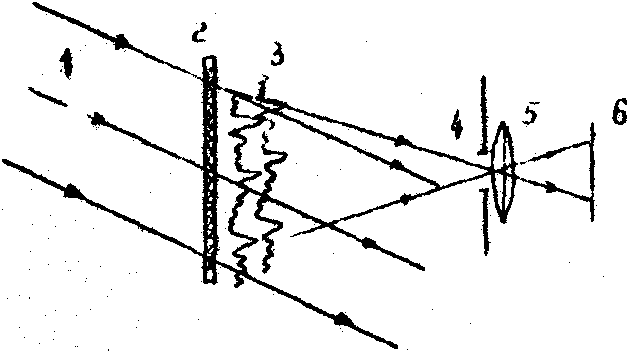
Рис.1. Схема получения спекл-интерферограмм:
1 - освещающий когерентный пучок;
2 - двухэкспозиционная спеклограмма;
3 - идентичные спекл-поля, рассеянные на спеклограмме;
4 - пространственный фильтр или апертурная диафрагма линзы 5;
6 - действительное изображение спеклограммы объекта.
Следовательно, взаимный пространственный сдвиг спокл-полей в плоскости спеклограммы; как правило, превышает размеры спеклов, которые, в свою очередь, определяют размеры элементарных областей пространственной когерентности спекл-поля /21/. Поэтому световые поля оказываются пространственно нескоррелированными, что препятствует образованию низкочастотной интерференционной картины - спекл-интерферограммы. Для получения такой картины необходимо привести преобразование световых полей, направленное на расширение элементарных областей пространственной когерентности спекл-полей. Такое преобразование можно выполнить на основе пространственной фильтрации исходного поля. В спекл-интерферометрии пространственную фильтрацию обычно проводят или и Фурье-плоскости, или и плоскости самой спеклограммы. Однако это не является принципиально необходимым - пространственную
фильтрацию для получения спекл-интерферограмм можно проводить и в любой другой области пространства. Например, на рис.1 приведена схема получения спекл-интерферограмм, в которой пространственная фильтрация осуществляется в области дифракции Френеля, где обычно проводят фильтрацию при получении голографических интерферограмм /10/. Предпочтительность пространственной фильтрации Фурье-плоскости обусловлена двумя непринципиальными практическими обстоятельствами - во-первых, в этой плоскости нерассеянным пучок занимает наименьшую область, во-вторых, получаемое изображение в целом имеет наиболее равномерную освещенность.
Комплексный коэффициент поперечной пространственной корреляции спекл-поля в результате пространственной фильтрации в соответствии с теоремой Ван-Циттерта-Цернике /4/ будет определяться выражением:
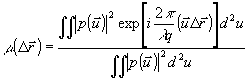 (1) (1)
где р( 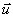 ) - функция амплитудного пропускания зрачка оптической системы, q - расстояние от входного зрачка до плоскости наблюдения, D
r = |
D ) - функция амплитудного пропускания зрачка оптической системы, q - расстояние от входного зрачка до плоскости наблюдения, D
r = |
D
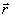 |
- расстояние между двумя точками в плоскости наблюдения. В (1) предполагается, что рассеянное на спеклограмме поле полностью заполняет зрачок и имеет постоянную среднюю интенсивность в его пределах. Если зрачок или, что то же самое, фильтрующее отверстие имеет форму круга с радиусом R и единичным амплитудным пропусканием, то (1) примет вид: |
- расстояние между двумя точками в плоскости наблюдения. В (1) предполагается, что рассеянное на спеклограмме поле полностью заполняет зрачок и имеет постоянную среднюю интенсивность в его пределах. Если зрачок или, что то же самое, фильтрующее отверстие имеет форму круга с радиусом R и единичным амплитудным пропусканием, то (1) примет вид:
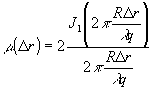 (2) (2)
Принимая за размеры области корреляции e
спекл-поля полуширину главного максимума функции (2), получим
e
= 1,22·l
q/2R (3)
Таким образом, для наблюдения спекл-интерферограммы необходимо, чтобы взаимное пространственное смещение спекл-полей, вызванное смещением поверхности объекта, не превышало величины e
. Это условие обычно выполняется для всего изображения при использовании достаточно малого диаметра 2 R фильтрующего отверстия. Однако при увеличении диаметра отверстия уменьшается величина e
и, как следствие, сокращаются размеры области, где наблюдается интерференционные полосы. Иными слонами, интерференционная картина приобретает ярко выраженный локализованный характер. Распределение видности полос в области локализации*) будет описываться для круглой апертуры выражениями (1) или (2), в которых D
r необходимо рассматривать как вектор взаимного смещения идентичных элементов интерферирующих спекл-полей. Для плоскости, оптически сопряженной с плоскостью спеклограммы, D
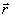 - вектор смещения элементов зарегистрированных спекл-структур. Максимальная видность полос будет иметь место в областях с минимальными значениями D
r. При увеличении D
r видность уменьшается и в соответствии с (1) это уменьшение, как и в голографической интерферометрии /11,12/, носит осциллирующий характер при использовании бинарных (неаподизированных) апертур. - вектор смещения элементов зарегистрированных спекл-структур. Максимальная видность полос будет иметь место в областях с минимальными значениями D
r. При увеличении D
r видность уменьшается и в соответствии с (1) это уменьшение, как и в голографической интерферометрии /11,12/, носит осциллирующий характер при использовании бинарных (неаподизированных) апертур.
*) В настоящем рассмотрении мы не учитываем декорреляцию зарегистрированных спекл-структур, имеющую место в результате продольного смещения поверхности объекта /20/. Не учитываем также и эффект декорреляции спекл-полей, вызываемый смещением спекл-поля в плоскости входного зрачка регистрирующей /22-25/ и наблюдательной оптических систем.
Рассмотрим конкретные примеры локализации полос в двухэкспозиционной спекл-интерферометрии при различных смещениях объекта.
1.1. Поперечный поступательный сдвиг объекта
В этом случае в плоскости спеклограммы объектные спекл-поля претерпевают поперечный поступательный сдвиг, а интерференционная картина, как и в голографической интерферометрии, Судет локализована в Фурье-плоскости, которая совпадает с изображением точечного источника, освещающего спеклограмму (рис.2).
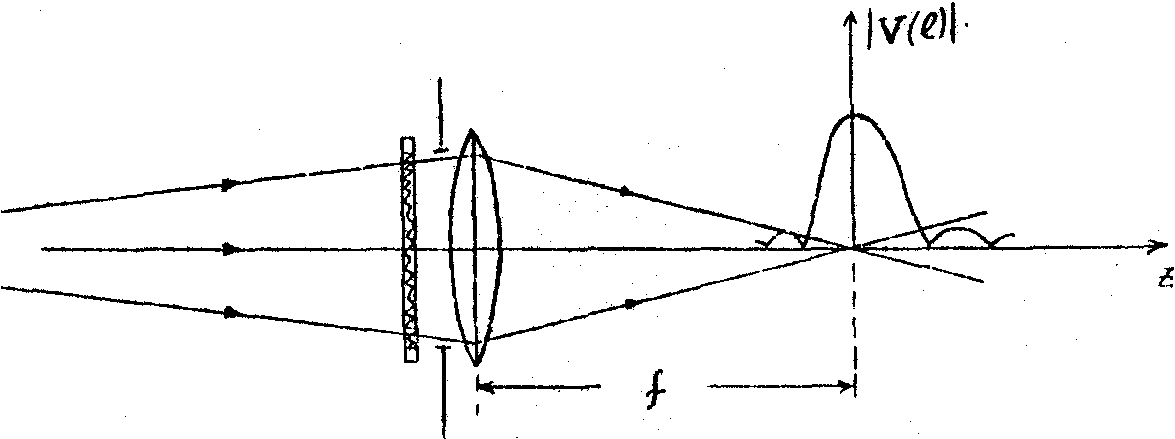
Рис.2. Наблюдение интерференционных полос при поперечном поступательном сдвиге спекл-структур и распределение видности этих полос в области локализации вдоль оптической оси.
Локализация полос именно в этой плоскости обусловлена тем обстоятельством, что в Фурье-плоскости отсутствует взаимное смещение объектных: спекл-полей. Отличия между этими поляки проявляются в линейном фазовом множителе exp{i 2p
gx
/l
ƒ} (где g - поперечный сдвиг спекл-структур, x
- координат в Фурье-плоскости), ответственным за образование прямолинейных эквидистантных полос с периодом
L
= l
ƒ/g
Поскольку в Фурье-плоскости спекл-поля не имеют взаимного сдвига, то видность полос |
V|
не зависит от размеров апертуры переотображающей линзы. Однако от апертуры зависит глубина области локализации полос, поскольку при выходе из Фурье-плоскости в ту или другую сторону объектные спекл-поля приобретают взаимное поперечное смещение D
r, определяемое выражением
D
r(ℓ) = gℓ/ƒ (4)
где ℓ - расстояние от Фурье-плоскости до рассматриваемой плоскости. Если используется круглая апертура, диаметр 2R которой меньше диаметра спеклограммы, то распределение видности полос вдоль оптической оси *) будет описываться функцией вида
|
V(ℓ)|
= |
2J1(u) / u|
, u = 2p
Rgℓ / l
ƒ(ƒ + ℓ) (5)
где использовано соотношение (4) и введено обозначение g = ƒ + ℓ. Из (5) следует, что распределение видности |
V(ℓ)|
имеет несимметричный характер относительно Фурье-плоскости. Нарушение симметрии объясняется тем, что при удалении от Фурье-плоскости в сторону линзы взаимный поперечный сдвиг D
r(ℓ) объектных спекл-полей увеличивается, а размеры области поперечной корреляции e
уменьшаются, тогда как при удалении от Фурье-плоскости в противоположную сторону обе эти величины возрастают. Нетрудно видеть, что когда размеры изображения на спеклограмме меньше апертуры Фурье-преобразующей линзы, а спеклограмма располагается в передней фокальной плоскости линзы, размеры области поперечной корреляции e
определяются
*) Здесь мы не принимаем во внимание пучок нулевого порядка дифракции, который в реальных условиях мешает наблюдать полосы непосредственно вдоль оптической оси.
не апертурой линзы, а размерами изображения, и остаются постоянными вдоль оптической оси. Следовательно, в данном случае распределение видности полос в области локализации будет иметь симметричный характер.
Принимая за глубину области локализации расстояние L между первыми нулями функции (5), получим
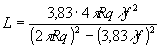
Следует отметить, что при удалении от оптической оси глубина области локализации полос увеличивается, поскольку размеры элементарных областей поперечной корреляции спекл-поля возрастают вследствие уменьшения угловой апертуры.
Пели спекл-интерферограммы получают путем освещения спекло-граммы нерасширенным лазерным пучком, то относительное смещение спекл-структур в пределах освещенного участка практически однородно как при жестком, так и при деформационном смещении поверхности объекта. Поэтому соответствующая интерференционная картина также локализована в Фурье-плоскости. Локализованный характер .полос в этом случае проявляется при достаточно большом g, если полосы наблюдать не в дальней плоскости дифракции свободного пространства, а в задней фокальной плоскости собирающей линзы при расположении спеклограммы в ее передней фокальной плоскости (рис.3). Поскольку интенсивность в поперечном сечении лазерного пучка имеет распределение Гаусса, то, в соответствии с (1), распределение видности полос в области локализации также будет описываться функцией Гаусса.
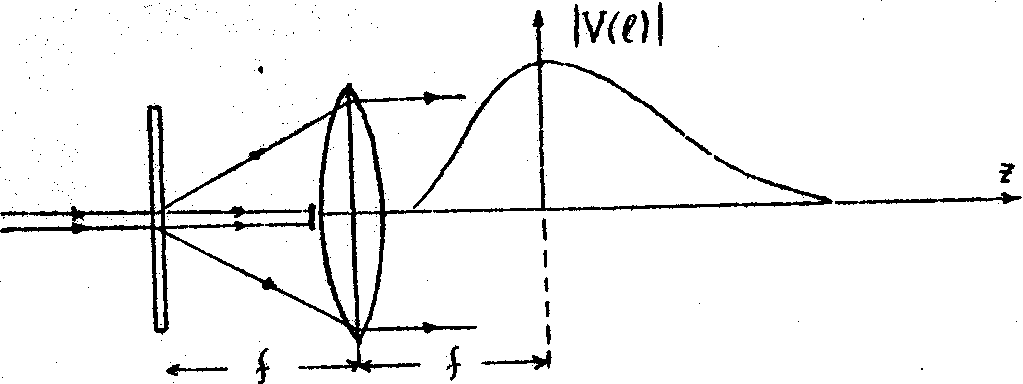
Рис.3. Схема наблюдения локализованных интерференционных полос при освещении спеклограммы нерасширенным лазерным пучком.
1.2. Наклон поверхности объекта
При наклоне поверхности объекта отсутствуют смещения субъективной спекл-структуры. Поэтому в этом случае регистрацию спеклограмм проводят в расфокусированной области /20,26/, где формируется объективная спекл-структура. Если поверхность объекта имеет неплоскую форму, то отдельные спеклы испытывают различное смещение в зависимости от макрорельефа и угла наклона /22/. Такое изменение спекл-структуры эквивалентно изменению, которое имеет место при деформации поверхности объекта. Но в плоскости Фурье-образа смещение спекл-структуры является однородным /26,27/ независимо от макрорельефа поверхности. Следовательно, если регистрацию спеклограмм проводить в Фурье-плоскости, то при наклоне объекта на двухэкспозиционной спеклограмме будут записаны две идентичные спекл-структуры, имеющие взаимный поперечный сдвиг g = ƒw
(1 + Cosg
), где w
- угол наклона, g
- угол падения освещающего пучка. Иными словами, реализуется случай, рассмотренный в предыдущем разделе, т.е. интерференционные полосы будут локализованы в
плоскости Фурье-образа светового поля, рассеянного на спеклограмме.
1.3. Продольное поступательное мещениэ объекта
Продольное поступательному смещению поверхности объекта сопутствует симметричное относительно оптической оси радиальное расширение (или сжатие) спекл-структуры в плоскости регистрации /23,28/. Поэтому спекл-поля, рассеянные на каждой записанной спекл-структуре, будут пространственно скоррелированы только в области, прилегающей к оптической оси. В этой области спекло граммы будут наблюдаться локализованные интерференционные полосы. Вне плоскости слеклограммы - по данной работе /29/ - поверхность локализации кольцевых интерференционных полос имеет форму параболоида вращения вокруг оптической оси с вершиной в плоскости спеклограммы. Геометрические параметры этого параболоида определяются величиной продольного смещения объекта и параметрами схемы записи спеклограммы. В /29/ рассматривалась регистрация спекл-структуры в плоскости Фурье-образа пропускающего диффузора, освещенного сходящейся сферической волной, что позволяет исключить декорреляцию спекл-структур вследствие их продольного смещения*).
1.4. Вращательный сдвиг объекта
Весьма интересным в методическом плане смещением является вращательный сдвиг объекта - поворот вокруг оси, перпендикулярной поверхности объекта. В этом случае имеет место центральная симметрия и линейное приращение смещений точек поверхности объекта. При этом отраженное от объекта спекл-поле также испытывает вращательный сдвиг на тот же угол w
. Если ось вращения совпадает с осью Z, а освещающий пучок лежит в плоскости
*) В настоящее время опубликована работа /35/, в которой детально рассматривается локализация полос в спекл-интерферометрии продольного смещения.
XZ и составляет угол g
с осью Z, то положение оси вращательного сдвига спекл-полей описывается /12/ уравнениями^
x = -z·Sing
, y = 0 (7)
При регистрации двухэкспозиционной спеклограммы в плоскости сфокусированного изображения на ней будут записаны две вращательно сдвинутые идентичные спекл-структуры с центром вращения на оптической оси *). Освещение полученной спеклограммы широким лазерным пучком приводит по аналогии с диффузно отражающим объектом к образованию за спеклограмме спекл-полей, имеющих взаимный вращательный сдвиг на угол w
. Ось этого вращательного сдвига совпадает с направлением освещения и проходит через центр вращения спекл-структур в плоскости спеклограммы. В пространстве изображений наблюдательной оптической системы (рис.4) объектные спекл-поля имеют вращательный сдвиг вокруг оси, поставляющей угол g
/b
к оптической оси (b
- поперечное увеличение). В области, прилегающей к этой линии, и будет локализована интерференционная картина, поскольку в этой области имеет место наименьшее взаимное смещение интерферирующих спекл-полей.
На pиc.5a представлена спекл-интерферограмма вращательного сдвига, полученная при использовании малого круглого фильтрующего отверстия. В этом случае интерференционные полосы наблюдаются в пределах всего изображения объекта, поскольку размер e
элементарной области пространственной корреляции, определяемый соотношением (3), превышает максимальное взаимное смещение спекл-полей в плоскости изображения. При увеличении диаметра фильтрующего отверстия область пространственной корреляции уменьшается, что приводит к сокращению области изображения, в которой наблюдаются интерференционные полосы (рис.5 б,в),
*) При регистрации спеклограммы в Фурье-плоскости центр вращательного сдвига спекл-структур, как это следует из (7), не лежит на оптической оси, а имеет координаты (-ƒSing
,0).
максимальная видность полос при этом имеет место в центре вращательного сдвига изображений.
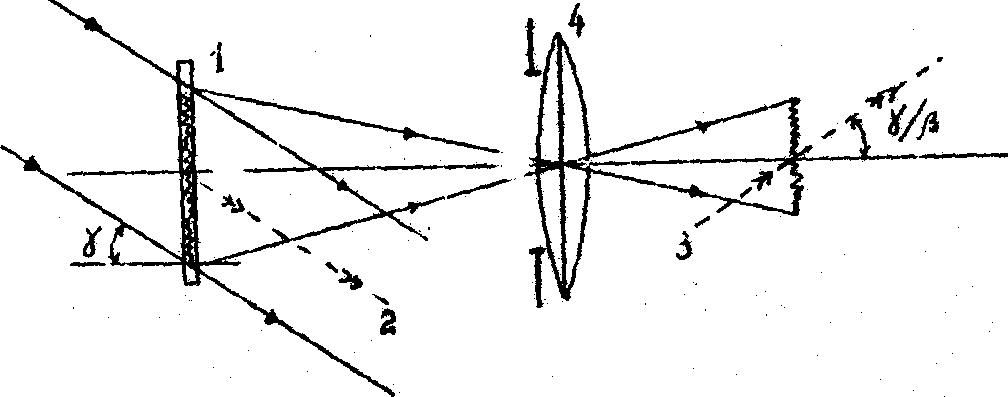
Рис.4. Схема наблюдения спекл-интерферограмм вращательного сдвига: 1 - двухэкспозиционная спеклограмма; 2 и 3 - оси взаимного вращательного сдвига спекл-полей, соответственно, в пространстве предметов и изображений наблюдательной оптической системы 4.
Поскольку линия локализации полос составляет угол g
/b
с плоскостью изображения объекта (рис.4), то при фокусировке объектива наблюдательной системы на плоскости перед изображением и за ним интерференционная картина должна смещаться в поле зрения в поперечном направлении вдоль проекции оси вращения спекл-полей на плоскость изображения. Этот эффект иллюстрируется рис.6. Заметим, что аналогичное явлений имеет место и в голографической интерферометрии (см. /5/, стр.146), поскольку голографическая интерферограмма вращательного сдвига также локализована на прямой линии.
 
а) б )

в)
Рис.5. Спекл-интерферограммы вращательного сдвига объекта на угол w
»
8', полученные при относительном отверстии объектива 1:16 (а), 1:5,6 (б), 1:2 (в) и b
= 0,26.
 
а) б)
Рис.6. Спекл-интерфарограммы вращательного сдвига, полученные при относительном отверстии 1:2 объектива наблюдательной системы при фокусировке в плоскость перед спеклограммой (а) и в плоскость за ней (б).
В спекл-интерферограммах вращательного сдвига так же, как и в голографических интерферограммах этого смещения /11,12/, наглядно проявляется осциллирующий характер видности полос. Осцилляции видности заметны при использовании круглого зрачка (см. рис.5б,в и рис.6), но наиболее ярко они выражены в случае применения зрачков сложной формы. На рис.7 представлены спекл-интерфврограммы вращательного сдвига, полученные со зрачками в виде кольца и двух круглых отверстий. При кольцевом зрачке распределение видности полос в соответствии с (1) будет описываться /11,12/ выражением:
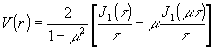 (8) (8)
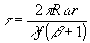 (9) (9)
где R - радиус внешней окружности кольца, m
R - радиус внутренней окружности кольца (0 < m
< 1), 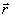 - радиус-вектор в плоскости изображения. - радиус-вектор в плоскости изображения.
Если используется зрачок, в виде двух круглых отверстий одинакового диаметра d, то распределение видности полос описывается выражением:
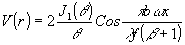 (10) (10)
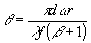
где b - расстояние между центрами отверстий, x - координата вдоль направления, перпендикулярного отрезку между центрами отверстий. Расстояние между отверстиями выбиралось таким, чтобы в пределах главного максимума функции 2J1(q
)/q
укладывалось несколько периодов функции 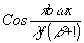
 
а) б)
Рис.7. Спекл-интерферограммы вращательного сдвига на угол w
»
8', полученные: а) с кольцевым зрачком: R = 14,5 мм, m
= 0,69; b
= 0,26, ƒ = 58мм, б) со зрачком в виде пары круглых отверстой, ориентированных поперек интерференционных полос.
2. Интерпретация спекл-интерферограмм
В предыдущем разделе, с точки зрения представлений, сложившихся в топографической интерферометрии, рассмотрено явление локализации полос в спекл-интерферометрии. Это позволило выявить ряд общих для этих методов особенностей в процессах формирования интерференционных картин, являющихся сигналами измерительной информации. На наш взгляд, полезно также рассмотреть интерпретацию спекл-интерферограмм с позиций, принятых в голографической интерференции.
Выше показано, что непосредственно за плоскостью двухэкспозиционной спеклограмму образуются два идентичных спекл-поля, имеющих поперечный сдвиг между идентичными элементами (спеклами). Эти световые поля в общем аналогичны полям в плоскости голографического изображения диффузно отражающей поверхности объекта, которая между экспозициями испытала только плоскостные смещения или деформации. В этом случае в плоскости изображения также формируются два спекл-поля, идентичные спеклы которых претерпели поперечный сдвиг. Это обстоятельство можно трактовать таким образом, что в двухэкспозиционной спекл-интерферометрии реализуется один из частных случаев голографической интерферометрии, когда поверхность объекта испытывает только поперечные смещения или деформации. Следовательно, для расшифровки спекл-интерферограммы можно применить известное в голографической интерферометрии /30/ соотношение:
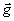 (x,y)[ (x,y)[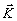 H(x,y) - H(x,y) - 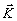 0(x,y)] = Nl
(11) 0(x,y)] = Nl
(11)
где x,y - координаты в плоскости спеклограммы, 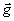 (gх,gy,0) - вектор смещения спеклов на спеклограмме, N - порядок интерференции, (gх,gy,0) - вектор смещения спеклов на спеклограмме, N - порядок интерференции, 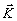 0 и 0 и 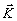 H - единичные векторы направлении освещения спеклограммы и наблюдения. В (11) учитывается, что d общем случае H - единичные векторы направлении освещения спеклограммы и наблюдения. В (11) учитывается, что d общем случае 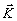 0 и 0 и 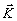 H зависят от координат x,y, чему соответствуют освещение спеклограммы сферической волной и наблюдение с конечного расстояния. H зависят от координат x,y, чему соответствуют освещение спеклограммы сферической волной и наблюдение с конечного расстояния.
Порядок интерференции N, как и в голографической интерферометрии, как правило, неизвестен. Для его определения необходимо, чтобы на изображении имелась полоса нулевого порядка и было известно ее местоположение. Эта полоса соответствует нулевому зарегистрированному смещению спеклов, поэтому она локализована на поверхности спеклограммы. Отыскать эту полосу можно или по максимальному контрасту полос в ее окрестностях при использовании большой апертуры наблюдательной системы, или по смещению полос при изменении направления наблюдения. В последней случае полоса нулевого порядка не смещается при изменении направления наблюдения*). Если отсутствует смещение спеклов на малом участке спеклограммы ли в отдельной ее точке, как, например, в случае вращательного сдвига или продольного поступательного смещения, то при изменении направления наблюдения этот участок не должны пересекать темные интерференционные полосы.
Порядок интерференции N можно установить и другим путем. Для этого необходимо определить величину смещения |
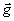 | в какой-либо точке спеклограммы. Эту величину можно измерить, проводя пространственную фильтрацию в плоскости спеклограммы. Зная величину | | в какой-либо точке спеклограммы. Эту величину можно измерить, проводя пространственную фильтрацию в плоскости спеклограммы. Зная величину |
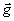 |
, из (11) легко определить N для данной точки, а, следовательно, и для других точен изображения. |
, из (11) легко определить N для данной точки, а, следовательно, и для других точен изображения.
*) Поперечное смещение самой спеклограммы не вызывает смещения полос относительно изображения, если пространственная фильтрация проводится в Фурье-плоскости. В этом случае полосы кажутся как бы связан ми со спеклограммой. Эта особенность, на наш взгляд, явилась еще одной причиной для ложного утверждения о локализованности спекл-интерферограмм на изображении объекта. В действительности же неизменность интерференционной картины объясняется постоянством вектора 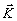 = = 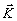 Н - Н - 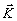 0 (см. (11)) при поперечном смещении слеклограммы. 0 (см. (11)) при поперечном смещении слеклограммы.
Поскольку интерференционные полосы не локализованы на спеклограмме, то для расшифровки спекл-интерферограмм можно применить метод счета полос, аналогичный известному методу расшифровки голографических интерферограмм /20/. В самом деле, предположим, что спеклограмма освещается плоской волной, перпендикулярно ее поверхности. Тогда для каждой точки изображения из уравнения (1) получим следующее соотношение:
gxCosa
i + gyCosb
i = Nil
(12)
где Cosa
i и Cosb
i - направляющие косинусы вектора 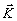 Hi. Hi.
Меняя направление наблюдения вдоль оси x при b
i = 90° и вдоль оси y при a
i=90° и подсчитывая количество полос D
Nx и D
Ny "пробежавших" через данную точку (x,y), изображения, из выражения (2) получим формулы для расчета составляющих gx и gy и вектора смещения:
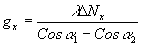 , , 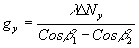 (13) (13)
Проведем также сравнение чувствительностей методов голографической и спекл-интерферометрии для плоскостных смещений или деформаций поверхности объекта. Если расшифровка интерферограмм проводится методом счета полос, то выходным измерительным сигналом служит число полос, "пробежавших" через выбранную точку изображения при измерении направления наблюдения на заданный угол. Чувствительность измерений будет определяться отношением произведения этого числа на длину волны к величине смещения в данной точке. Поскольку установлено, что наблюдаемые полосы в обоих методах могут быть описаны одними и теми же соотношениями (10) или (11), нетрудно видеть, что чувствительности рассматриваемых методов равны. Иными словами, при изменении направления наблюдения на один и тот же угол, через точки, претерпевшие равные смещения, "пробежит" одинаковое число интерференционных полос. При этом исходные и конечные углы направлений наблюдения должны быть одинаковыми в схемах голографической и спекл-интерферометрии.
Далее равним пороговые чувствительности этих методов. Под пороговой чувствительностью в настоящем рассмотрении следует понимать наименьшую регистрируемую часть периода интерференционной полосы, пересекающую данную точку изображения при максимально возможном изменения угла наблюдения. В спекл-интерферометрии диапазон изменения углов наблюдения ограничивается угловыми размерами дифракционного гало, которые, в свое очередь, определяются выходной апертурой регистрирующей оптической системы /26,31/. В голографической интерферометрии эти ограничения также определяются или апертурой голограммы, или апертурой линзы (в схемах голографии Фурье и сфокусированных изображений).
Рассмотрим идентичные схемы получения голограммы и спеклограммы, что можно выполнить путем совместной регистрации, например, голограммы и спеклограммы в плоскости сфокусированного изображения при использовании относительно слабого по интенсивности опорного пучка /32/. Нетрудно показать /28,31/, что в этом случая угловые размеры 2j
светового гало в нулевом порядке дифракции связаны с угловыми размерами 2g
светового пучка в первом порядке дифракции соотношением
Sin2j
= 2Sin2g
(14)
Отсюда следует, что метод спекл-интерферометрии имеет в два раза меньший порог чувствительности, чем голографическая интерферометрия, если принять равной точность измерения доли интерференционной полосы в обоих методах.
Нетрудно видеть, что аналогичное превышение пороговой чувствительности спекл-интерферометрии над пороговой чувствительностью голографической интерферометрии можно получить и по отношению к голографическим схемам Фурье, Денисюка и Френеля. В последнем случае двухэкспозиционные спеклограммы следует получать путем регистрации действительного изображения, восстановленного сопряженным опорным пучком с голограммы Френеля /33 /.
Очевидно также, что, при использовании пространственной фильтрации в плоскости спеклограммы и голограммы, в дифракционных
гало нулевого и первого порядков будут наблюдаться прямолинейные полосы одинаковой ориентации и равного периода. При этом, в силу соотношения (14) общее число полос в нулевом порядке будет в два раза больше числа полос в первом порядке дифракции.
Если в качестве сигнала измерительной информации рассматривается пространственный период интерференционных полос, наблюдаемых на изображении с одного направления, то для получения одинаковой голографических спекл-интерферограмм необходимо, чтобы углы освещения объекта и спеклограммы, а также углы наблюдения изображений были бы, соответственно, одинаковыми. В голографической интерферометрии за счет схемных решений, например, при использовании скользящего направления освещения и наблюдения в обратном направлении /5/. может быть реализована более высокая чувствительность к плоскостным смещениям, чем в спекл-интерферометрии. Однако в этом случае фактически имеют место нормальные смещения, к которым методы голографической интерферометрии наиболее чувствительны.
Таким образом, при использовании идентичных оптических схем методы голографической и спекл-интерферометрии имеют равную чувствительность к смещениям поверхности в плоскости *). Это объясняется тем, что в основе обоих методов лежат единые физические механизмы образования интерференционных картин.
Заключение
В методах голографической и спекл-интерферометрии полосы образуются в результате суперпозиции идентичных спекл-полей, имеющих взаимный пространственный сдвиг, обусловленный смещением или деформацией поверхности объекта между экспозициями.
*) В /15,34/ показано, что при измерении изгибных деформаций методом голографической и спекл-интерферометрии с регистрацией спеклограммы в расфокусированной области может быть достигнута одинаковая пороговая чувствительность этих методов.
В связи с этим процессом формирования интерференционных полос в этих методах подчиняются единым закономерностям. Это проявляется в парную очередь в локализованном характере интерференционных картин, получаемых обоими методами, и в идентичности распределения видности полос в области локализации, включая эффекты осцилляции видности. В силу того, что в голографической интерферометрии регистрируется не только пространственное смещение спекл-полей, но и их фазовые возмущения, в этом методе пространственное положение областей локализации отличается большим разнообразием, чем в спекл-интерферометрии. Например, голографические интерференционные картины локализуются в плоскости изображения, когда имеют место только изгибные деформации или только наклон поверхности объекта. В результате таких смещений в плоскости изображения слекл-поля приобретают фазовую модуляцию при незначительном, по сравнению с размером области корреляции пространственном смещении, о спекл-интерферометрии - на спеклограмме всегда регистрируется поперечное смоление спеклов без фазовой модуляции, что исключает возможность получения в плоскости спеклограммы локализованной интерференционной картины.
Поскольку в основе образования интерференционных картин в голографической и спекл-интерферометрии лежит единый физический механизм, то расшифровку этих картин можно проводить одинаковым образом. В частности, в спекл-интерферометрии можно применять способы интерпретации, разработанные для голографической интерферометрии. Такой единый подход к анализу голографических и спекл-интерферограмм упрощает сравнительные исследования метрологических возможностей этих методов и позволяет оценивать их практические достоинства.
Рассматривая методы голографической и спекл-интерферометрии как средства обеспечения суперпозиции идентичных спекл-полей следует отметить, что такая суперпозиция может быть реализована и без процедуры фоторегистрации и последующего восстановления исходного спекл-поля. Для этого могут быть использованы классические схемы интерферометров, например, Мяйкельсона или Маха-Цендера, в которых в качестве источника света используется
диффузор, освещенный когерентным светом. На выходе такого интерферометра будут распространяться два идентичных спекл-поля, различия между которыми в фазовом макрорельефе и взаимном пространственном смещении обусловлены различиями в плечах интерферометра. За счет соответствующей юстировки оптических элементов в плечах интерферометра можно добиваться совпадения идентичных спеклов двух спекл-полей в различных областях пространства и, следовательно, получать локализованные интерференционные картины, подобные интерференционным картинам в голографической интерферометрии. Наблюдение интерференционной картины в таком интерферометре можно также осуществлять, используя оптическую систему с малой апертурой, обеспечивающую расширение области пространственной корреляции спекл-полей.
Литература
1. Борн М., Вольф Э. Основы оптики — М.: Наука, 1970, 655с.
2. Островский Ю.И., Бутусов М.М., Островская Г.В. Голографическая интерферометрия – М.: Наука, 1977, 336с.
3. Власов Н.Г., Пресняков Ю.П. Пространственная корреляция интенсивности в диффузно-когерентном излучении и интерференционные измерения на её основе. // Современные проблемы прикладной голографии - М., МДНТП, 1974, с.13-32.
4. Goodman J.W. Statistical properties of laser speckle patterns. – In: Laser speckle and related phenomena. -Helldelberg.: Springer-Verlag, 1975, p.9-75.
5. Вест. Ч. Голографическая интерферометрия: Пер. с англ. /Под ред. Ю.И.Островского - М.: Мир, 1962, 504с.
6. Briers J.D. The interpretation of holographic interferograms. Review. - Opt. Quant.Electron., 1976, vol.6, N.6, p.469-501.
7. St etson К.A. Problem of defocusing in speckle photography, its connection to hologram interferometry, and its solutions. - J.Opt.Soc.Am., 1976. vol.66, N.11, p.1267-1271.
8. Yamaguchi I. Fringe loci and visibility in holographie interferometry with diffuse objects: Fringe of equal thickness. - Opt.Acta, 1978, vol.25, N.4, p.299-314.
9. Jaeguot P., Rastodi P.K. Speckle motions induced by rigid-bady movements in free-space geometry: on explicit investigation and extension to new cases. - Appl.Opt., 1979, vо1.18, N.12, р.2022-2032.
10. Клименко И.Р., Рябухо B.D. Пространственная фильтрация в голографической интерферометрии. // Вопросы прикладной голографии. Материалы Х IV школы по голографии. -Л.: ЛИЯФ, 1982, р.62-80.
11. Клименко И.Р., Рябухо В.П., Федулеев Б.В. Проявление тонкой структуры спекл-полей при их когерентном сложении. - Письма в ЖТФ, 1963, т.9, вып.21, с.1381-1385.
12. Клименко И,Р., Рябухо В.П, Федулеев Б.В. Проявление тонкой структуры спекл-полей при их интерференции. // Методы и устройства оптической голографии. Материалы Х V школы по голографии - Л.: ЛИЯФ, 1983, с.70-103.
13. Пресняков Ю.П., Царфин Е.Я. О влиянии дифракции в голографической интерферометрии в диффузно-когерентном излучении. - ЖНИПФИК, 1976. т.21, № 2, с.100-103.
14. Stetson К.A. Hologram interferometry and speckle metrology: a retrospective look.- Opt.Hews, 1979, vol.5, N.4, р.14-16.
15. Ennos А.E. Comparative accuracy of holographic interferometry and speckle photography for out-of-plane defomation measurement.- Opt.Commun., 1980, vol.33, N.1, р.9-12.
16. Голографическая интерферометрия. Обзорная информация. Сер. Метрологическое обеспечении измерений /Н.Г.Власов, Р.Б.Мацонашвили, А.Б.Штанько, В.И.Горчков - М.: Госстандарт, 1984, вып.1, 53 с.
17. Cloud О. Practical speckle interferome try for measuring in-plane deformation.-Appl.Opt., 1975, vol.14, N4, p.876-884.
18. Жилкин В.А., Борыняк Л.А. Оптические способы определения малых перемещений и деформаций элементов конструкций. // Голографические измерительные системы - Новосибирск, 1976, с.76-92.
19. Применение спекл-интерферометрии для контроля качества промышленных изделий. Методические указания - Горький, Горьковский филиал ВНИИНМАШ госстандарта СССР, 1980, 137 с.
20 . Франсон М, Оптика спеклов. Пер. с англ. / Под ред. Ю.И.Островского - М.: Мир, 1960, 171 с.
21. Власов Н.Г., Штанько А.Е. Некоторые вопросы голографической интерферометрии. // Материалы VIII Всесоюзной школы по голографии - Л.: ЛИЯФ, 1976, с.202-221.
22. Богомолов А.С., Власов Н.Г., Штанько А.Е. Исследование рельефа диффузно-отражающих объектов методом спекл-топографии с открытой апертурой - ЖТФ, 1978, т.48, вып.8, с.1696-1699.
23. Богомолов А.С. Власов Н.Г., Штанько А.Е. Влияние корреляции волновых полей на чувствительность голограмм - ЖТФ, 1979, т.49, вып.6, с. 1737.
24. Yamaguchi I, Speckle displacement and decorrelation in the diffraction and image fields for small object deformation.- Appl.Opt., 1981, vol.20, N.19, p.3392-3402.
25. Spajer M., Rastogi Р.К., Monneret J. In-plane displacement and strain measurement by spe ckle interferometry and moire derivation. - Appl.Opt., 1981, vol.20, N.19, p.3392-3402.
26. Tiziani H.J. A study of the laser speckle to measure small tilts of optically rough surfaces accurately. - Opt.Commun., 1372, vol.5, N.4, p.271-276.
27. Клименко И.Р., Рябухо В.П., Федулеев Б.В., Лохова Н.В. Об особенностях голографических и спекл-интерферограмм, получаемых при регистрами объектного светового поля в Фурье-плоскости. - Оптика и спектроскопия, 1963, т.55, вып.3, с.483-469.
28. Archbold В., Еnnоs А.E. D isplacement measurement from double-exposure laser photographs.- Optica Acta, 1972, v.19, N.4, p.253-271.
29. Hagopian J., May К. Interference phenomena generatid bу two radially shifted speckle patterns, - J.Opt., 1976, v.9, N.4, р.217-226.
30. Александров Е.Б., Бонч-Бруевич А.М. Исследование поверхностных деформаций тел с помощью голограммной текинки. – ЖТФ, 1967. т.37, № 2, с.360-369.
31. Megnard R. Diffraction halo in speckle photography. - Appl.Opt., 1984, vol.23, N.14, р.2235-2242.
32. Adams F.D., Maddux G.E. Synthesis of holography and speckle photography to measure 3-D displacements. -Appl.Oppl., 1974. v.13, N.2, p.219.
33. Гусев К.Г., Капустин А.А., Рассоха Д.А. Количественная оценка голографических интерферограмм с помощью спекл-интерферометрии. // Материалы IX Всесоюзной школы по голографии - Л.: ЛИЯФ, 1977, с. 267-286.
34. Еnnоs А.Е., Virdee M.S. Laser speckle photography as a practical alternative to holographic interferometry for measuring plate deformation. - Opt.En, 1982, v.21, N.3, p.478-48 2.
35. Марквида И.В., Танин Л.В., Уткин И.А. Локализация интерференционной картины в спекл-фотсграфии продольно смещаемых объектов. - ЖТФ, 1968, т.58, в.1, с.121-124.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

