|
|
 |
 |

|
| |
АПОДИЗЛЦИЛ (л.-ИЧКЖИХ СИСТЕМ
Н.Г.Власов, Б.К.Кинбер, З.Г.Семенов, С.В.Карпеев
В классической оптике, полностью когерентное освещение встречалось относительно редко и задачи фильтрации пространственных частот, в том числе проблема аподизации, не стояли на переднем плане. Положение существенно изменилось с развитием когерентной оптики и методов оптической обработки информации, и в настоящее время эта задача достаточно актуальна. В данной работе ее решение дается сначала для дифракционных оптических элементов, получен-hex голографическими методами, а затем для классических, обычных объективов и линз.
До развития голографии перечень оптических элементов, действие которых основано на явлении дифракции, ограничивался дифракционными решетками и зонными пластинками. Положение существенно измоталось с появлением голографии, когда было обращено внимание на перспективность самого направления дифракционной оптики и предложены принципиально новые оптические элементы, не имеющие классического аналога /1/. Голографический метод формирования оптических элементов и в настоящее время остается актуальным. К его достоинства относятся, в частности, возможность изготовления оптических элементов, предназначенных для работы в пределах всего видимого диапазона, тиражирование прецизионных, в том числе крупногабаритных объектов, возможность получения сложных оптических элементов за счет последовательной записи отдельных составляющих на один и тот же участок, регистрирующей среды и т.д.
Метод аподизации, описываемый в настоящей: работе, позволяет существенно подавить вторичные максимумы импульсного отклика, характерные для оптических элементов, работающих в когерентном лазерном
излучении. Его идея поясняется при помощи схемы на рис.1, представляющей модернизированный вариант получения голографической линзы, предложенной в /1/. На регистрирующую среду 1 направляются расходящаяся 2 и сходящаяся 3 сферические волны (рис.1), интерференция которых и образует микроструктуру голограммы-линзы с фокальной длиной ƒ, определяющейся соотношением 1/ƒ =1/а+1/b, где a н b - расстояния от голограммы до центров кривизны сферических волн. В отличие от /1/ голограмма записывается двумя экспозициями, между которыми центр кривизны одной из волн смещается в продольном направлении на величину d
= 2l
(а/d)2, где d - действующий диаметр голограммы.
Нетрудно показать, что при одновременном действии двух источников, расположенных на таком расстоянии, середина образованного ими первого темного интерференционного кольца совпадает с апертурой голограммы-линзы. Таким образом, разность фаз световых полей, восстановленных такой голограммой в ненулевых порядках дифракции, плавно изменяется от нуля в центре до p
на краях апертуры, где они находятся в противофазе, что и приводит к заметному ослаблению вторичных максимумов. Заметим, что величина d
равна двум продольным размерам основного максимума импульсного отклика (или, что то же самое, двум продольным размерам диска Эйри), поэтому два изображения, создаваемые такой линзой, по отношению к друг другу расфокусированы незначительно и практически совпадают.
Если же необходимо аподизировать щелевую апертуру, то перед второй экспозицией центр кривизны источника излучения смещается не в продольном, а в поперечном направлении. Интерференционная картина имеет тогда вид параллельных эквидистантных прямых, параллельных краям щелевой апертуры, причем светлая интерференционная полоса проходит через центр, а две ближайшие к ней темные - по краям апертуры. Выполнение этого условия обеспечивает косинусоидальное распределение полк по апертуре, максимум которого приходится на центр апертуры, а минимумы - на края.
Отметим, что рассматривавши метод позволяет аподизировать и обычные оптические элементы, действие которых основано на эффектах преломления и отражения. Дня этого изготавливается голограмма,
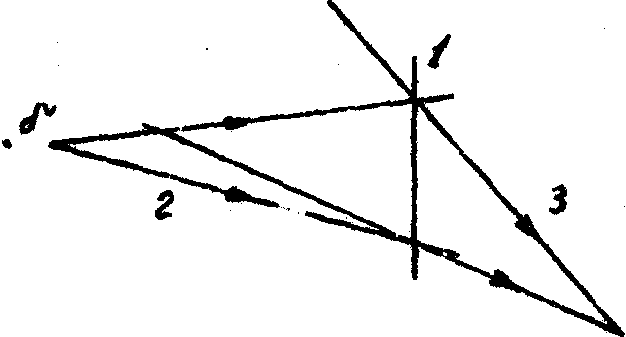
Рис.1. Схема получения аподизированной голограммы - линзы.
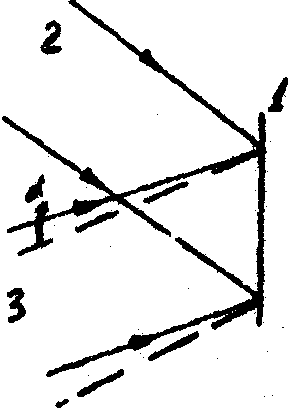
Рис.2. Схема получения голограммы - аподизирующей маски для щелевой апертуры.
например, с нулевой оптической силой, обеспечивающая требуемое распределение поля по апертуре и располагаемая затем вблизи аподизируемого объектива. Так для аподизации объектива со щелевой апертурой, краями которого в нашем проверочном эксперименте были лезвия бритвы, голограмма 1, образованная двумя плоскими волнами 2 и 3, записывалась по схеме рис.2 методом двойной экспозиции. Между экспозициями одна из плоских волн поворачивалась на малый угол ~ 0,1 мин., тогда период интерференционных полос на восстановленном изображении равнялся примерно 1 см. Полученная голограмма располагалась неподалеку от объектива так, чтобы центры соседних темных полос проходили через края апертуры. Визуальное наблюдение в микроскоп показало, что вторичные максимумы импульсного отклике при этом значительно ослабляются. Для сравнения апертура смещалась так, что через ее края проходили середины светлых полос. Вторичные максимумы тогда вновь становились яркими. Методика изготовления приставки для аподизации круговой апертуры отличается незначительно: одна из плоских волн между экспозициями при записи голограммы несколько изменяется по кривизне так, чтобы диаметр первого темного интерференционного кольца совпал с диаметром аподизируемой апертуры.
На примере щелевой апертуры перейдем к количественной оценке, для чего воспользуемся результатами, полученными для анализа дифракционного изображения в теории антенн /2/. В связи с тем, что названная теория хорошо разработана, отметим только, что косинусоидальному распределению поля по апертуре, имеющему место и в этом случае, соответствует импульсный отклик n(u) вида:
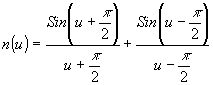 (1) (1)
в котором вторичный максимум номера " n" одного слагаемого накладывается в противофазе на максимум номера "n+1" другого слагаемого, в результате происходит ослабление первого, второго и третьего вторичных максимумов, соответственно, на 9,6; 12,3; 15,2 децибел.
История развития науки показывает, что решение какой-либо научной задачи редко бывает единственным. Попытка нахождения других
решений рассматриваемой задачи привела к идеи записи на голограмму дифракционной картины на микроотверстии, пространственное распределение поля в которой обеспечивает получение импульсного отклика и требуемыми характеристиками.
Простейшим критерием для выбора дифракционной картины может служить требование совпадения формы отверстия, предназначенного для создания картины дифракции, с идеализированным импульсным откликом, то есть с откликом, имеющим только нулевой максимум, с пространственными размерами и формой, определяемыми только дифракцией на апертуре оптической системы. Отсюда следует, что микроотверстие должно быть таким, чтобы картина дифракции на нем соответствовала размеру и форме апертурной диафрагмы. Уточним это положение. Как уже отмечалось, сходная с аподизацией проблема решалась в антенной технике /2/, где она формулировалась как задача определения и создания в раскрыве антенны поля, обеспечивающего диаграмму направленности с ослабленными вторичными максимумами и с энергией, сосредоточенной в основном в нулевом максимуме. Решение названной задачи привело к выводу, который в общем виде можно сформулировать как необходимость создания в раскрыве поля, имеющего максимум в центре, с плавным спаданием до нуля на краю раскрыва. Этот вывод не противоречит полученному выше, а только уточняет его в том смысле, что микроотверстие должно иметь такие размеры и форму, чтобы линия одного из минимумов картины дифракции на нем при записи аподизирующей голограммы или при ее использовании совпадала с краями апертурной диафрагмы. Так, для прямоугольной апертуры, частным случаем которой является целевая, картина дифракции имеет, как известно /3/, вид совокупности светлых, похожих на эллипсы фигур, разграниченных темными минимумами, на темном фоне, что позволяет осуществить несколько вариантов диафрагмирования с краями диафрагмы, проходящими по центрам минимумов. Напомним, что для прямоугольного отверстия дифракционная картина по координате Х или У описывается функцией вида Sin(x)/x и угловые размеры минимумов ~ Nl
/h, где l
- длина волны, h - ширина щели в направлении, перпендикулярном рассматриваемой координате, N - целое число, что позволяет просто рассчитать параметры
схемы записи.
В антенной технике и описанному выше общему виду аподизирующей функции иногда добавляют небольшой постоянный пьедестал. В принципе, его нетрудно получить, записывая дополнительной экспозицией на голограмму волновой поле с постоянной амплитудой, однако применение такой аподизирующей маски приведет одновременно и к появлению в плоскости изображения постоянного мешающего фона поэтому такой вид аподизации далее не обсуждается.
Рассмотрим, в качестве примера, решение задачи аподизации голографического оптического элемента, являющегося аналогом цилиндрической линзы. Схема записи голограммы показана на рис.3,
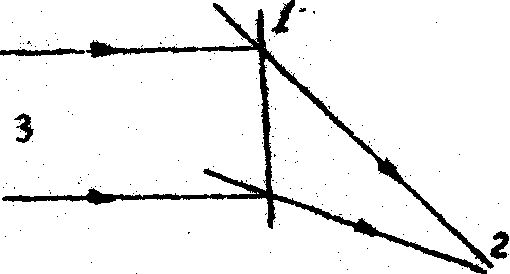
Рис.3. Схема получения голограммы - аподизированной цилиндрической линзы.
плоская опорная волна 3 падает на фотопластинку - голограмму 1 вместе с объектным волновым полем, образующим за ней, а помощью вспомогательной цилиндрической линзы, изображение 2 щелевого микроотверстия в непрозрачном экране. Само микроотверстие с экраном и линзой для упрощения чертежа не показаны. Как уже отмечалось, область, где записывается голограмма на регистрирующей среде, должна быть ограничена одним из минимумов дифракционной картины, образованной щелевым микроотверстием. Если осветить полученную голограмму, то она преобразует ее в сходящуюся цилиндрическую волну, то есть подействует как аподизированная цилиндрическая волна. Вернемся теперь к схеме записи аподизирующей голографической приставки, не изменяющей фокусирующих свойств классического оптического элемента, то есть схему получения голограммы с нулевой
оптической силой. Известно, что такими свойствами обладает голограмма Фурье. Следовательно, аподизирующую голограмму следует записывать либо по схеме обычной линзой, либо по схеме безлинзовой голографии Фурье (см., например, /4/). Как уже отмечалось, форма микроотверстия определяется аподизируемой апертурой. Так, для аподизации щелевой, прямоугольной и круговой апертуры требуются, соответственно, щелевое, прямоугольное и круговое отверстия. В последнем случае аподизирующая функция будет иметь вид I1(Z)/Z, где I1(Z) - функция Бесселя.
Маскирование апертуры приводит к тому, что количество пропущенного ею света уменьшается, так как уменьшается ее эффективный размер. По этой же причине несколько ухудшается разрешение. В антенной техника для описания этих эффектов вводят понятие апертурного коэффициента использования и полной ширины главного максимума, определяемого по его нулевому значению. Расчет на ЭВМ показал, что для аподизирующей функции S in(x)/x и диафрагмы с краями, совпадающими, соответственно с первым, вторым и третьими минимумами этой функции, ширина главного максимума, нормированная на единицу для аподизированной апертуры, равна 1,65; 1,3; 1,25; а апертурный коэффициент использования равен 0,72; 0,35; 0,19.
Чтобы найти весь спектр решения и обобщить полученные результаты, запишем амплитудное пропускание голограммы с аподизацией в первом порядке дифракции в виде:
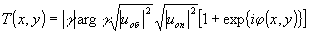 (2) (2)
где х,у - координаты в плоскости голограммы, g
- нормированная функция взаимной когерентности объектного и опорного волновых полей, j
(х,у) - изменение фазы между экспозициями. Для рассматриваемых здесь голограмм Френеля и Фурье объектное или опорное волновой полу описывается, как известно, сверткой функций амплитудного пропускания микроотверстия, которое может находиться в одном или обоих плечах схемы записи голограммы и освещающего волнового поля. В выражении (2) функция argg
описывает фазу восстановленного волнового поля и высокочастотную модуляцию (несущую пространственную частоту), обеспечивающую пространственное разделение различных порядков
дифракции и линейную передачу (восстановление) остальных функций, входящих в (2). Таким образом, для аподизации в любых сочетаниях могут пользоваться функции: когерентности, временной и пространственной, освещающего излучения, амплитудного пропускания объектов и изменения разности фаз волновых полей между экспозициями. В частности, еще один вид аподизирующего распределения ноля по апертуре оптической системы - гауссовское, можно получить за счет использования одномодового режима работы лазера. Аподизирующие характеристики этого распределения приведены в /2/.
Отметим, что в оптической обработка информации сходные с аподизацией задачи решались с помощью двойного преобразования Фурье с фильтром пространственных частот, помещенной в Фурье-плоскости. В настоящей работе развивается другой подход, основанный на том, что фильтр пространственных частот вписывается в дифракционный оптический элемент (объединяется с ним) в процессе их изготовления. Отметим также , что в некоторых методах аподизации требуемое распределение поля по апертуре достигается за счет интерференции волновых полей, осуществляемых с помощью голографического оптического элемента. Вместо этого можно было бы применить, например, интерферометр Майкельсона, однако его применение существенно усложнит аподизацию по стоимостным, массово-габаритным и виброзащитным параметрам.
В заключение рассмотрим преимущества и недостатки голографических методов аподизации. К преимуществам, в первую очередь, относится возможность линейной записи и воспроизведения аподизирующей функции независимо от характеристик регистрирующей среды. Действительно, в голографии ее нелинейность приводит к появлению высших, по сравнению с первым, порядков дифракции, что не искажает линейную передачу в первом порядке, используемом для практического применения. К недостаткам относятся относительно невысокая дифракционная эффективность голограмм, записанных на традиционных регистрирующих средах-фотоэмульсиях, и внеосевое, по отношению к оси аподизируемой оптической системы, направление распространения аподизированного изображения, однако, современные регистрирующие среды типа хромированной желатины и реоксана практически свободны от первого недостатка, их дифракционная эффективность
близка к единице. Второй недостаток не носит, по нашему мнению, принципиального характерами способ его устранения в дальнейшем может быть разработан.
Литература
1. Власов Н.Г., Скроцкий Г.В., Мосякин Й.С. Квантовая электроника, 1972, № 7, с.14-19.
2. Ямпольский В.Г., Фролов О.П. Антенный ЭМС. М., Радио и связь, 1963, 272 с.
3. Борн М., Вольф Э. Основы оптики. М., Наука, 1973, 720 с.
4. Сороко Л.М. Основы голографии и когерентной оптики, 1971.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

