О ВОЗМОЖНОСТЯХ ОПТИЧЕСКОЙ ДИАГНОСТИКИ СТРУКТУРЫ ФАЗОВЫХ СЛУЧАЙНЫХ ОБЪЕКТОВ
О.В.Ангельский, П.П.Мяксимяк
В работе представлены корреляционно-оптические методы определения структуры фазово-неоднородиых объектов. Методы основаны на использовании модели случайного фазового экрана. Экспериментальные исследования подтвердили эффективность методов. Задача решена и для случая, когда статистика распределения фазовых неоднородностей отличается от гауссовой.
I. Введение
Постановка задачи об оптической диагностике фазово-неоднородных объектов требует рационального выбора способа описания самого объекта. Известно, что полное описание поля случайного объекта предполагает знание n-мерных плотностей вероятности для данного поля, т.е. предполагается заданной функция распределения плотности вероятности случайной величины.
Поле оптического излучения, взаимодействуя со случайным фазовым объектом, наполняется информацией об объекте.
Поэтому задача диагностики структуры произвольного случайного объекта должна решаться в два этапа:
- нахождение взаимосвязи статистических параметров структуры объекта и соответствующих корреляционных параметров поля в зависимости от зоны регистрации;
- исследование возможности экспериментального измерения корреляционных параметров поля.
II. Элементы модели ц постановка задачи.
Для описания взаимодействия оптического излучения с фазово-неоднородным объектом используем модель случайного фазового экрана (СФЭ) /1/. Модель СФЭ предполагает:
- в формировании поля излучения, провзаимодействовавшего с объектом, принимают участие все пространственно-частотные компоненты поля, соответствующие фазовой структуре объекта:
- дисперсия фазы неоднородностей объекта s
2j
0 < 1;
- радиус корреляции неоднородностей ℓj
0 случайного фазового объекта больше длины волны, т.е. ℓj
0 > l
.
Наиболее просто, традиционно, решается задача диагностики структуры в случае, если предположить статистику объекта гауссовой. В этом случае, для полного описания структуры объекта достаточно найти среднее значение случайной величины и ее дисперсию.
Известно много оптических вариантов решения задачи определения дисперсии фазы случайного объекта. Специально, этому вопросу посвящено ряд обзоров и оригинальных работ /2-3/. Идея предлагаемых методов проста - существует однозначная взаимосвязь дисперсии фазы объекта и относительного контраста спекл-структуры поля, провзаимодействовавшего с объектом. Измерение контраста спекл-структуры в разных зонах регистрации поля, включая и зону формирования изображения поверхности, позволяет определить дисперсию фазы объекта. Общей сложностью на путях реализации этих методов является необходимость в априорной информации о количестве неоднородностей, участвующих в формировании поля, и выполнение достаточно длительной операции сканирования по полю с последующей статистической обработкой результатов.
III. Предлагаемые подходы и результаты исследований.
Первой из упомянутых трудностей в измерениях дисперсии фазы объекта. связанной с необходимостью априорной информации, можно избежать, используя подход, заимствованный из радиофизики и предложенный Рытовым /1/. Согласно этому подходу, индекс мерцаний поля в дальней зоне (зоне Фраунгофера) равен удвоенному значению дисперсии фазы объекта:
b
2¥
= 2s
2j
0 (1)
Таким образом, экспериментально обеспечивая требование безгранично-протяженного объекта и провода в дальней зоне (по отношению к одной неоднородности) сканирование поля в поперечном направлении можно найти индекс мерцаний поля b
2¥
, определяемый соотношением
b
¥
= s
2J/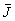 2
2
(где s
2J - дисперсия интенсивности, 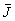 - среднее значение квадрата интенсивности). Экспериментальные исследования выполнялись в расположении, показанном на рис.1. В качестве объектов исследования здесь и в дальнейшем использовались пластины из плавленного кварца и отражающие пластины монокристаллического германия /4/.
- среднее значение квадрата интенсивности). Экспериментальные исследования выполнялись в расположении, показанном на рис.1. В качестве объектов исследования здесь и в дальнейшем использовались пластины из плавленного кварца и отражающие пластины монокристаллического германия /4/.
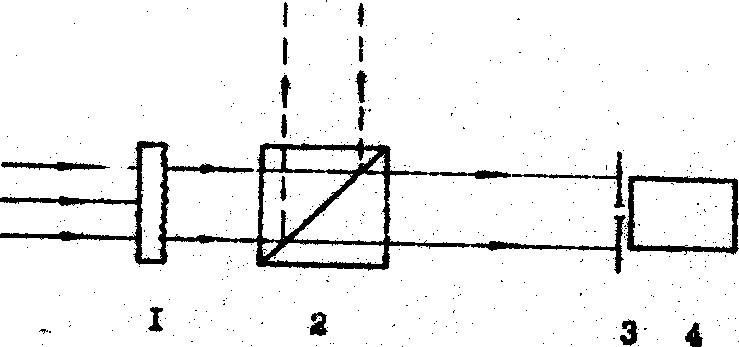
Рис.1. Схема измерений индекса мерцаний поля:
1 - исследуем объект; 2 - светоделительный куб, 3 - микронная диафрагма; 4 - фотоумножитель.
Достоинство рассмотренного метода в том, что независимо от статистики объекта диагностика дисперсии фазы неоднородностей его возможна и достаточно точна.
Второй метод диагностики использует взаимосвязь поперечной функции когерентности Г^
(r
) поля, провзаимодействовавшего с объектом со статистическими параметрами собственно объекта /1/:
Г^
(r
) = ехр{s
2j
0[Kj
0(r
) – 1]} (2)
где Кj
0(r
) - коэффициент корреляции фазы. В основу получения соотношения (2) положено предположение о гауссовой статистики объекта. Немаловажно и то, что для объектов с s
2j
0 < 1 поперечная функция когерентности поля Г^
(r
) равна поперечной функции когерентности граничного поля Гv(r
), независимо от зоны регистрации поля. Из (2) видно, что, логарифмируя правую и левую части соотношения можно получить выражение непосредственно доя дисперсии фазы объекта.
Задавая поперечное смещение r
между оптически смешиваемыми компонентами, при экспериментальном измерении Г^
(r
), большим нежели радиус корреляции неоднородностей объекта ℓj
0, добиваются Кj
0(r
) = 0 и получают непосредственно значение s
2j
0.
Экспериментальные исследования выполнялись в схеме, представленной на рис.2 - модифицированной схеме интерферометра Маха-Цандера. Схема предполагает возможность исследования как оптически-прозрачных, так и отражающих объектов. В зависимости от природы объекта используют пучок I либо II в осветительной части системы. Объект облучался по нормали пучком с плоским волновым фронтом. В интерферометре 8 осуществлялось амплитудное расщепление излучения, провзаимодействовавшего с объектом, на две равноинтенсивные составляющие, относительное поперечное смещение расцепленных составляющих с их последующим смешением. На выходе интерферометра смешанные пучки распространялись строго коллинеарно. С помощью объектива 9 произвольное сечение поля излучения, провзаимодействовавшего с объектом, проецировалось в плоскость полевой диафрагмы 11 Апертурная диафрагма 10 использовалась для управления спектром регистрируемых пространственных частот. Совокупность элементов 9-10-11-12 составляла систему продольного сканирования поля. Поперечное смещение между расщепленными пучками в
интерферометре Маха-Цандера сопровождается продольным смещением такой же величины, что не всегда желательно. В ситуации, когда необходимо избавиться от относительного продольного смещения смешиваемых компонент, можно использовать поляризационный интерферометр /5/.
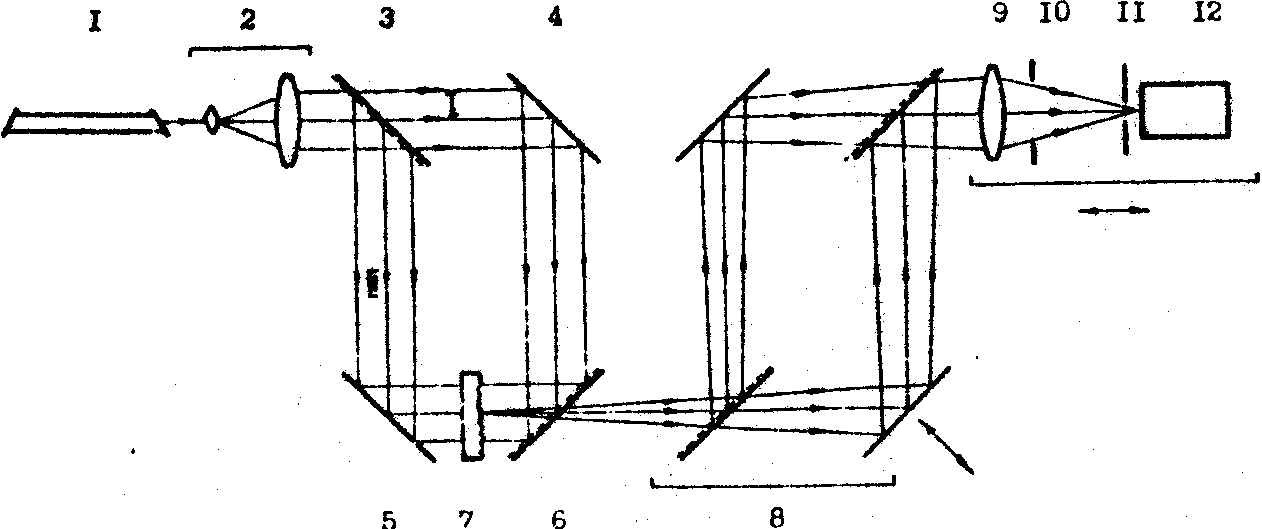
Рис.2. Схема измерения поперечной функции когерентности поля: 1 - лазер; 2 - телескопическая система; 3,6 - светоделители; 4,5 - зеркала; 7 - объект; 8 - интерферометр Маха-Цандера; 9 - объектив; 10,11 - апертурная и полевая диафрагмы; 12 - фотоприемник.
Третий вариант диагностики дисперсии фазы объекта основан на том, что в дальней зоне регистраций поля дисперсия амплитуды поля s
2А = ½s
2j
0 равна половине дисперсии фазы объекта /1/. В этом случае необходим метод прямого независимого измерения дисперсии амплитуды поля. Нами предложен интерференционный метод измерения дисперсии амплитуды поля /6/. Можно показать, что в случае интерференции соосно распространяющихся пучков -объектного и опорного - минимум интенсивности результирующего поля Js min может быть достигнут только в случае, когда средняя фаза объектной волны 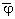 (х,y) противоположна фазе опорной
(х,y) противоположна фазе опорной
волны j
0: 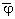 (х,у) = j
0 + p
, средняя амплитуда объектной волны,
(х,у) = j
0 + p
, средняя амплитуда объектной волны, 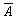 (х,у)=А0 равна амплитуде опорной А0, т.е.
(х,у)=А0 равна амплитуде опорной А0, т.е. 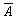 (х,у) = <A(x,y)> = A0. В этом случае:
(х,у) = <A(x,y)> = A0. В этом случае:
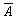 (х,у)2 = <A(x,y)>2 = A20 = J0 (3)
(х,у)2 = <A(x,y)>2 = A20 = J0 (3)
где J0 - интенсивность опорной волны. Известно, что дисперсия амплитуды поля s
2A определяется как
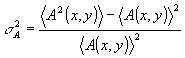 (4)
(4)
В соотношении (4) <A2(х,у)> - осредненная по площади интенсивность объектного пучка J(х,у), легко измеряемая величина. Значение же <А(х,у)>2 непосредственно измерять не представляется возможным. Однако, с учетом (3) можно утверждать, что значение этого слагаемого удается получить в результате измерения интенсивности опорной волны J.
Экспериментальные наследования возможностей этого метода выполнялись в схеме, представленной на рис.3.
Корректная постановка всех предложенных экспериментальных исследований предполагает такой выбор апертурных условий, который гарантировал бы выполнение приближения безгранично-протяженного случайного объекта. Иными словами, измерения корреляционных параметров поля уместно проводить в области, где присутствуют все пространственно-частотные составляющие поля рассеянного излучения. В случае, когда размер ограничивающей круглой диафрагмы а значительно превышает радиус корреляции граничного поля ℓj
0, вблизи ограничивающего отверстия имеется область, где влияние границ диафрагмы на корреляционные характеристики поля ничтожно. Указанная область представляет собой конус с основанием радиуса а/2 и высотой Z1 /1/:
Z1 = k·aℓj
0 (5)
где k = 2p
/l
. Однако, при прохождении излучения сквозь случайный базовый объект могут реализовываться эффекты фокусировок парциальных сигналов.
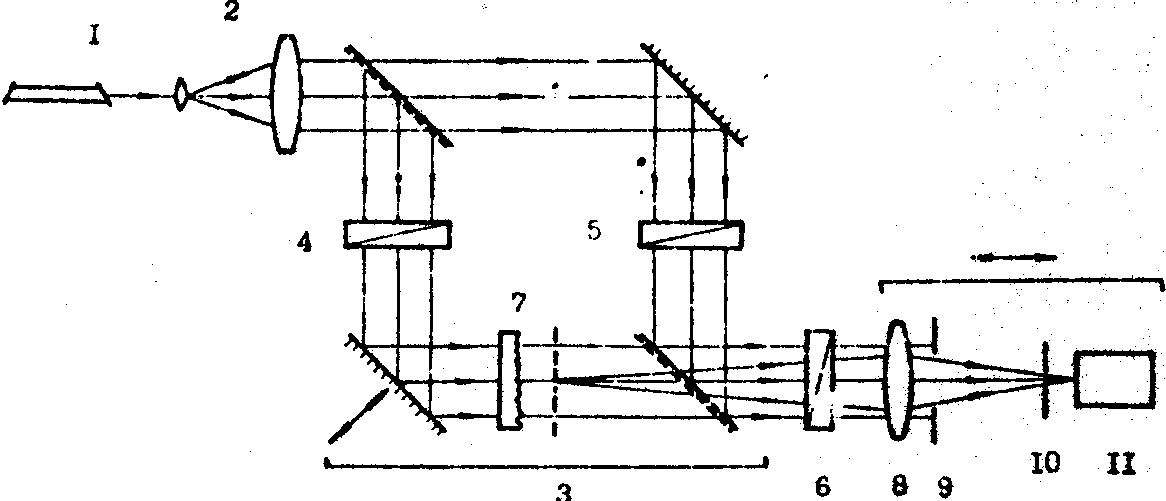
Рис.3. Схеме измерений корреляционных моментов поля:
1 - лазер; 2 - телескопическая система; 3 - интерферометр; 4,5,6 - поляроиды для управления интенсивностью пучков; 7 - исследуемый объект; 8 - объектив; 9,10 - апертурная и полевая диафрагмы; 11 - фотоприемник.
В области фокусировок флуктуации интенсивности поля максимальны. Положение этих максимумов зависит от кривизны фазового фронта граничного поля и определяется соотношением:
Zm = kℓj
0/s
j
0 (6)
По мере возрастания Z, т.е. по мере приближения зоны регистрации поля к дальней, происходит насыщение индекса мерцаний и дисперсии амплитуды поля и становится справедливым соотношение (1). Эта область соответствует зоне Фраунгофера Z¥
.
При изменении значения дисперсия фазы исследуемого объект изменяется местоположение зоны фокусировок парциальных сигналов к высоте конуса, в пределах которого присутствуют все пространственно-частотные составляющие, соответствующие фазовой структуре случайного объекта. Поэтому, при выборе зоны регистрации
поля необходимо учитывать как апертурную ограниченность объекта, так и значение фазовой дисперсии объекта s
2j
0. Так, при измерении поперечной функции когерентности поля зона регистрации Z должна удовлетворять условия
0 £
Z < Z1 (7)
для объекта с s
2j
0 < 1. Оптимальная зона регистрации индекса мерцаний, а значит, и дисперсии амплитуды поля, определяется из условия:
Z¥
£
Z < Z1 (8)
для объекта с s
2j
0 < 1.
Результаты проведанных исследований представлены я таблице.
Таблица
|
№
образца |
s
2j
0k |
s
2j
0K |
s
2j
0b
|
s
2j
0A |
|
1 |
0,059 |
0,057 |
0,052 |
0,057 |
|
2 |
0,095 |
0,087 |
0,080 |
0,102 |
|
3 |
0,118 |
0,120 |
0,113 |
0,125 |
|
4 |
0,140 |
0,139 |
0,126 |
0,145 |
|
5 |
0,433 |
0,405 |
0,341 |
0,380 |
|
6 |
0,115 |
0,125 |
0,102 |
0,120 |
|
7 |
0,422 |
0,400 |
0,376 |
0,376 |
|
8 |
0,720 |
0,580 |
0,503 |
0,550 |
Здесь в различных колонках приведены результаты измерений дисперсии фазы восьми случайных фазовых объектов разними способами: профилометрическим s
2j
0k, по индексу мерцаний s
2j
0b
, по поперечной функции когерентности поля s
2j
0K, по дисперсия амплитуды поля s
2j
0А. Относительное отклонение результатов измерений не превышает 25%.
Вместе с тем, в более общем случае, когда статистика объекта не гауссова, диагностика его структуры предполагает знание не только двух первых моментов фазы поля, но и моментов более высокого порядка. Только в этом случае возможно нахождение функция
распределения плотности вероятности случайной величины.
Рассмотрим результат интерференции двух волн, распространяющихся соосно: плоской и квазиплоской (фазово-модулированной объектной). Результат их интерференции можно представить с помощью следующего соотношения:
JS(x,y) = A20 + A2(x,y) + 2A0A(x,y)Cosj
(x,y) (9)
где JS(x,y) - интенсивность результирующего поля; А(х,у),А0 – амплитуды соответственно, объектной и опорной волн; j
(х,y) - разность фаз опорной и объектной воля.
В предположении о том, что <А(х,у)> = А0, a 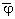 (x,y) = j
0 + p
и считая j
(x,y) < 10º соотношение (9) после осреднения по площади и ряда преобразований можно привести к виду /7/:
(x,y) = j
0 + p
и считая j
(x,y) < 10º соотношение (9) после осреднения по площади и ряда преобразований можно привести к виду /7/:
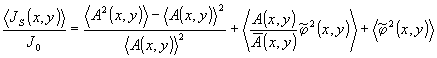 (10)
(10)
Проанализируем это соотношение.
Прежде всего, в граничном поле отсутствуют флуктуации амплитуды, поэтому дисперсия амплитуды поля 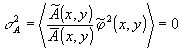 . Мы получаем возможность прямого интерференционного измерения дисперсии фазы объекта в граничное поле в соответствии с соотношением, вытекающим из (10):
. Мы получаем возможность прямого интерференционного измерения дисперсии фазы объекта в граничное поле в соответствии с соотношением, вытекающим из (10):
<JS(x,y)>/J0 = s
2j
0 (11)
Во-вторых, владея независимым способом определения s
2А и используя тот факт, что s
2j
0 = s
2j
+ s
2А независимо от зоны регистрации поля, могло доводить опенку смешанного корреляционного момента поля 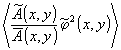 в любой зоне регистрации.
в любой зоне регистрации.
И, наконец, в-третьих, в области граничного поля можно находить корреляционные моменты фазы поля третьего и четвертого порядков однозначно и прямо характеризующие коэффициенты асимметрии Ка и эксцесса КЭ соответствующих функций распределения случайной величины.
Вид этих соотношений достаточно простой и следует из (11):
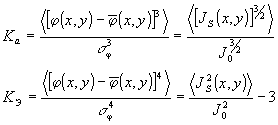 (12)
(12)
Зная корреляционные моменты фазы поля случайного объекта вплоть до момента 4-го порядка, можно находить функцию распределения плотности вероятности соответствующей случайной величины /8/.
Экспериментальные исследования выполнялись в схеме, представленной на рис.3 для отражающих поверхностей монокристаллов германия, параметры которых соответствовали модели случайного фазового объекта.
На рис.4 показан типичный ход экспериментально полученных зависимостей s
2А, s
2j
и 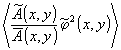 от зоны регистрации поля Д = 2Z/kℓj
. Их анализ показывает, что действительно в дальней зоне s
2А = s
2j
= ½s
2j
0, независимо от статистики объекта, максимум значения
от зоны регистрации поля Д = 2Z/kℓj
. Их анализ показывает, что действительно в дальней зоне s
2А = s
2j
= ½s
2j
0, независимо от статистики объекта, максимум значения 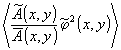 приходятся на зону фокусировок парциальных сигналов. Все это свидетельствует в пользу оптимальности выбора экспериментальных условий диагностики фазовой структуры случайных объектов в предлагаемых способах диагностики.
приходятся на зону фокусировок парциальных сигналов. Все это свидетельствует в пользу оптимальности выбора экспериментальных условий диагностики фазовой структуры случайных объектов в предлагаемых способах диагностики.
На рис.5 представлены функции распределения, полученные для слабошероховатой поверхности монокристалла германия профилометрическим и оптическим способами. Налицо хорошее соответствие результатов. Уверенно регистрируется отклонение статистики поверхностной структуры объекта от гауссовой
IV. Заключение
В заключении хотелось бы отметить, что рассмотренный комплекс исследований положен в основу разработки соответствующих методов диагностики структуры случайных фазовых объектов. Разработанные методы являются оригинальными, в большинстве случаев реализованы в виде макетов, выгодно отличаются быстродействием и высокой чувствительностью. Быстродействие достигается за счет осуществления операции статистического осреднения по полю и оптическом тракте. Предел чувствительности методов при контроле слабошероховатых поверхностей составляет 0,005 мкм.
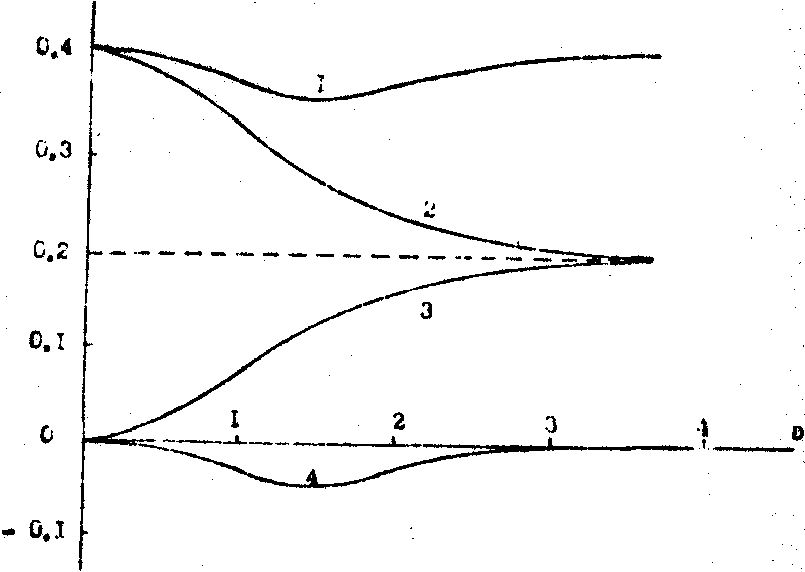
Рис. 4. Графики зависимостей <JS(x,y)>/J0 (кривая 1), s
2j
(кривая 2), s
2A (кривая 3) и 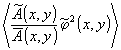 (кривая 4) от зоны регистрация поля образца монокристалла германия (Д = 2Z/kℓj
).
(кривая 4) от зоны регистрация поля образца монокристалла германия (Д = 2Z/kℓj
).
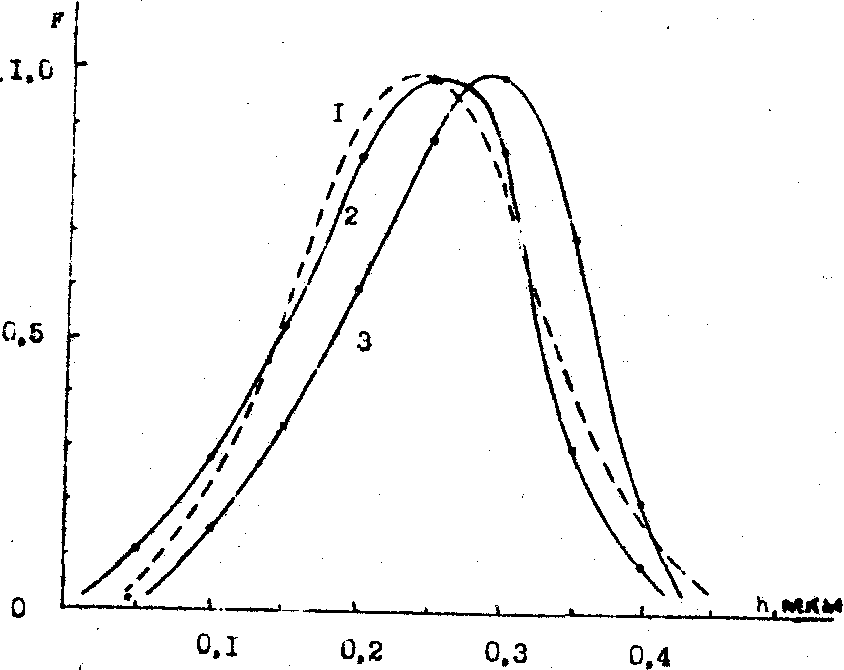
Рис.5. Функции распределения F микронеровностей поверхности образца, достроенные по результатам:
1 - гауссово распределение; 2 - профилометрических измерений; 3 - оптических измерений.
Литература
1. Рытов С.М,. Кравцов Ю.А., Татарский В.И. Введение в статистическую радиофизику, ч.2. Случайные поля. М.; Наука. 1978, 446 с.
2. Моисеев В.Н., Мандросов В,И. Информативность пятнистых когерентных изображений // Зарубежная радиоэлектроника. 1982, № 2, с.3-21.
3. H.Fujii, Asakura and Y.Shindo. Measurement of surface roughness properties by means of laser speckle techniques. Opt, Communs. 1976, 16, c.68.
4. Ангельский О.В., Житарюк В.Г., Максимяк П.И. О возможности корреляционно-оптического исследования фазово-неоднородных статистических поверхностей // Опт. и спектр, 1986, 60. вып.5, с.1013-1017.
5. Ахманов С.А., Дьяков Ю.Е., Чиркан А.С. Введение в статистическую радиофизику и оптику. М., Наука, 1981, 640 с.
6. O.V.Angelsky, P.P.Maksimyak, and Т.O.Perun, Optical correlation systems for studying weak aurface roughness, Frlnge'89, Automatic Processing of Fringe Patterns, Akademic-Verlag, Berlin.1989, c.53.
7. O.V.Angeleky, I.I.Magun, and P.P.Maksimyak, Optical correlation methods in the studles of inhomogeneous phase samples, Proc. IIId Internal.Symp.Mod.Opt., vol.2, Budapest. 1968, c.337.
8. M.G.Kendall, The Advanced Theory of Statistics, vol.1. Distribution Theory, A.Stuart. Ch. Griffin Co. Ltd. London. 1960.

