Media-security

ГОЛОГРАФИЧЕСКИЕ И КОСВЕННЫЕ МЕТОДЫ ИЗМЕРЕНИЯ ВРЕМЕННЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ

Т.И.Кузнецова

К настоящему моменту в литературе описано несколько моментов регистрации временных характеристик излучения, основанных на применении опорной волны. Поскольку эти методы базируются на идеях, близких к идеям, используемым при голографировании изменяющихся в пространстве стационарных полей, мы их будем называть голографическими. Ниже мы перечислим эти методы и укажем на одну их существенную особенность, которая связана именно с применением опорной волны. После этого перейдем к обсуждений альтернативных методов.

Первое предложение по голографической регистрации временных характеристик световых палеи было сформулировано /1/. В этой работе, а также в /2,3/ рассматривалась запись кис времен' них, так и пространственных характеристик, но здесь для краткости мы будем говорить только о зависимости поля от времени. При таком упрощении суть метода можно изложить следующие образом.

Пусть имеется пола сигнала e _S(t) и поле опорной волны E₀(t,x):

E_S(t) = e (t)exp[-iw t] (1)

здесь w - частота несущей, которая лежит в оптическом диапазоне. огибавшая e (t) - комплексная, функция с характерным временем изменения t _S:

E₀(t,x) = e ₀(t,x)exp[-iw t] (2)

причем e ₀(t,x) - огибающая опорной волны - должна в области –Д<х<Д иметь вид:

e ₀(t,x) = exp[-iaxt - iw xSina /c] (3)

а диапазон частот, содержащихся в огибающей, должен удовлетворять условию

1/t ₀ º aД ³ 1/t _S (4)

Сигнальный пучок падает под прямым углом на светочувствительный материал, а опорный - составляет с нормалью угол a . Величина засветки фотопластинки Н_полн с точностью до постоянного множителя будет выражаться формулой

Н_полн = Н₀ + Н(х) + Н^*(х) (5)

где

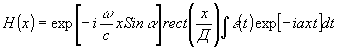(6)

Из выражения (6) видно, что интерференционное слагаемое Н(х) содержит Фурье-образ сигнала. Если ввести для Фурье-образа обозначение

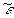(W ) º Le (t) = ò e (t)exp[-iW t]dt (7)

то можно вместо (6) записать

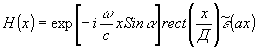(8)

Таким образом информация о спектре сигнала оказывается переведенной в координатную зависимость интенсивности почернения фотопластинки и частоты интерференционных полос. При выполнении условия (4) записанная информация является полной, и по ней впоследствии может бить восстановлен комплексный сигнал e (t).

Экспериментальная реализация этого метода записи и восстановления сигнала изложена в /4/.

Отметим, что формирование опорной полны нужного вида, по существу, эквивалентно получению одиночного короткого импульса длительности t ₀. Определим, какой вид будет иметь поле опорной волны вида (3) в дальней зоне. Нетрудно получить для дальней зоны зависимость

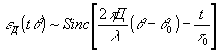(9)

здесь введена угловая координата q = x/z, z - расстояние от рассматриваемой плоскости до плоскости, в которой опорная волна имеет вид (3), q = Sina - угол, соответствующий максимуму интенсивности в дальней зоне в начальный момент времени. Из (9) следует, что, поместив в дальней зоне диафрагму, выделяющую угловой интервал D q , равный l /2Д, мы будем наблюдать непосредственно за диафрагмой импульс излучения длительности t ₀. (Эта ситуация иллюстрируется рисунком 1).

Вместе с тем ясно, что если в нашем распоряжений имеется одиночный световой импульс нужной длительности, то из него можно получить опорную волну вида (3). В работе /5/ обсуждается формирование опорной волны такого вида при пропускании одиночного короткого импульса через спектральный прибор.

Существуют и другие способы использования коротких импульсов для записи временных сигналов. Л именно, на использовании опорного импульса основаны эхо-голография временных сигналов /6/ и специальный случай эхо-голографии - запись сигналов в высокоселективных фотохромных средах с долгоживущим откликом /7/. Необычные свойства светочувствительных материалов, используемых в эхо-голографии, обеспечивают высокую информационную емкость при записи.

Известна также схема записи временных сигналов /рис.2./, использующая короткие импульсы (без спектрального разложения) и традиционные фотоматериалы (см., например, /8/).Эта схема действует следующим образом. Диаметры сигнального пучка и опорного пучка,

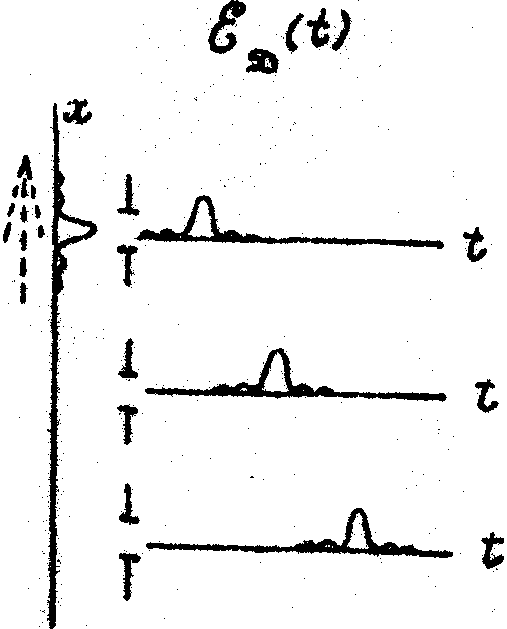
Рис.1. Поле нестационарной опорной волны в дальней зоне.

Рис.2. Схема записи временного сигнала, соответствующая работе /8/; опорной волной служит короткий импульс, наклонно падающий на фотопластинку.

несущего короткий импульс, расширяются так, чтобы поперечные размеры их были заметно больше продольного размера импульса сt ₀. При этом опорный пучок направляется на фотопластинку под малым углом, и время прихода импульса оказывается различным для различных значений координаты. Сигнальный пучок падает на фотопластинку нормально. Используя снова для пучков выражения вида (1) и (2), мы теперь должны взять функцию e ₀ в виде

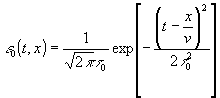(10)

для интерференционного слагаемого в засветке фотопластинки при этом получим

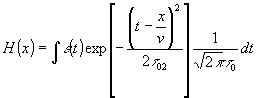(11)

Если опорный импульс является достаточно коротким, t ₀ < t _S, то вместо (11) можно написать

H(x) = e (x/v) (12)

Таким образом, в отличие от случая, который описывается формулой (8), означающей соответствие координата - спектр, здесь мы имеем соответствие координата – время. Укажем на одно исследование, выполненное с помощью этого метода. В работе /9/ научалось изменение импульса при прохождении через волоконный световод. Было зарегистрировано уширение импульса.

Общим для всех перечисленных методов является использование опорной волны (опорного импульса). Требования, предъявляемые к опорной волне, ограничивают круг исследований. Действительно, центральные частоты сигнала и опорной волны должны совпадать. Эффекты дрожания частоты реальных источников затрудняют осуществление этого условия. Поэтому оказывается, что не для всякого вида излучения удается подобрать опорную волны и провести с ней запись временных характеристик. Фактически в экспериментах, описанных в литературе, всегда речь идет об исследовании того излучения,

которое возникает из имеющегося импульса, когда он подвергается каким-то искажениям. Например, в вышеупомянутой работе /9/ исходный импульс искажался в световоде.

Если же стоит задача регистрации излучения, о свойствах которого заранее ничего не известно, то методы в таком виде перестают работать. Вместе с тем, наиболее интересной задачей было бы исследование излучения, которое не связано с заданным источником и для которого поэтому нет. подходящей опорной волны. В связи с этим напомним, что для изучения лазеров с синхронизацией мод в 1967 году были предложены так называемые косвенные методы исследования временных характеристик. Эти методы основаны на нелинейно-оптических эффектах, в первых вариантах - на двухфотонном поглощении или на генерации второй гармоники /10,11/. Для выполнения измерений исследуемое излучение расщепляется на два идентичных пучка, которые направляются а нелинейную среду; регистрация квадратичного аффекта дает информацию об автокорреляционной функции К(t ),

K(t ) = ò I(t)I(t + 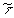)dt, I(t) = | e (t)| ² (13)

Первоначально метод предназначался дан измерения длительности одиночных импульсов; длительность легко определить по ширине пика автокорреляционной санкции. Однако исследуемое излучений может представлять собой группу импульсов или одиночный импульс асимметричной формы. В таком случае вид автокорреляционной функции усложняется. Дополнительные сложности привносятся шумами регистрирующей аппаратуры, искажающими вид автокорреляционной функции. Впрочем, в последнее время все больше применяются варианты косвенных методов с низким уровнем шумов /12,13/. В условиях высокой точности измерений можно пытаться проводить математическую обработку зарегистрированных данных. Подобные подходы разрабатывались в литературе для задач восстановления пространственных характеристик световых полей по автокорреляционным функциям /14,15/. Мы хотим обратить внимание на целесообразность применения алгоритмов, сходных с алгоритмом из работы /14/, к

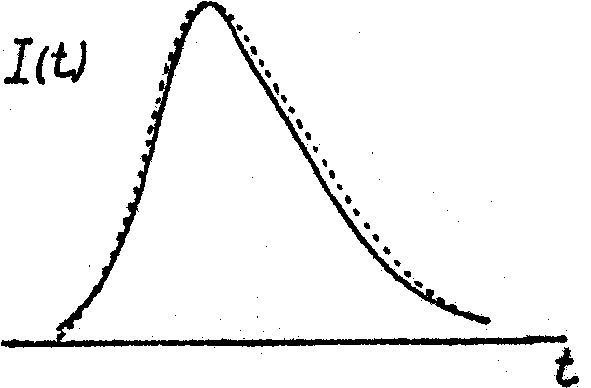
временным измерениям. Мы рассматривали одномерные функции, моделирующие зависимость интенсивности от времени, и пробовали восстанавливать их по функции автокорреляции. Отметим прежде всего, что метод работая абсолютно надежно, если мы имели дело с одиночным импульсом во временном ходе I(t). По автокорреляции удавалось не только получить оценку ширины импульса, но и воcстановить его форму. Во всех опробованных- случаях (с одиночным импульсом) итерационная процедура всегда сходилась либо к I(t), либо к I(-t). Если допустить, что априорные данные позволяют выбрать одно из двух таких решений, то можно говорить об однозначности восстановления. На рис.3 приводится иллюстрация к восстановлению одиночного импульса. Сплошными линиями

а)

б)

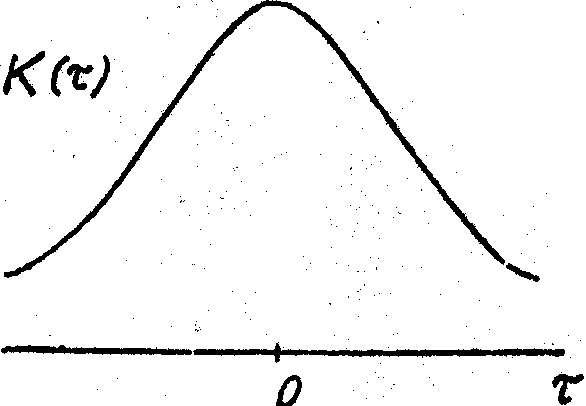
Рис.3. Восстановление асимметричного импульса по его автокорреляционной функции. Сплошными линиями изображены исходный импульс (а) и его автокорреляционная функция (б), штриховой линией - импульс, полученный после 10 итераций при восстановлении.

изображены асимметричный импульс (а) и его автокорреляционная функция (б). Штриховой линией изображен импульс, полученный по данным об автокорреляционной функции с помощью итерационного алгоритма за 10 итераций. Если же выполнить 100 итераций, то вид полученного импульса уже будет практически неотличим от истинного.

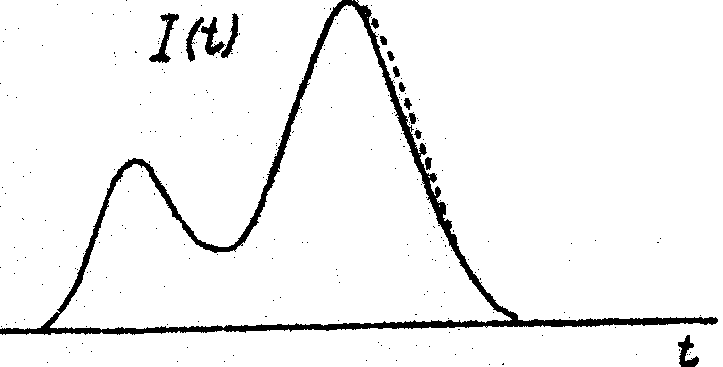
Так же успешно проходило восстановление в случае, когда исходное излучение содержало два симметричных импульса разной амплитуда, но одинаковой формы. Иллюстрация к одному из таких расчетов приводится на рис.4.

а)

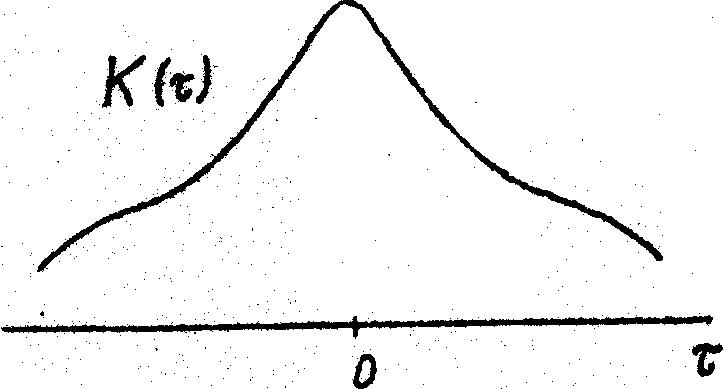
б)

Рис.4. То же, что на рис.3, но для исходных временной картины, состоящей из двух импульсов.

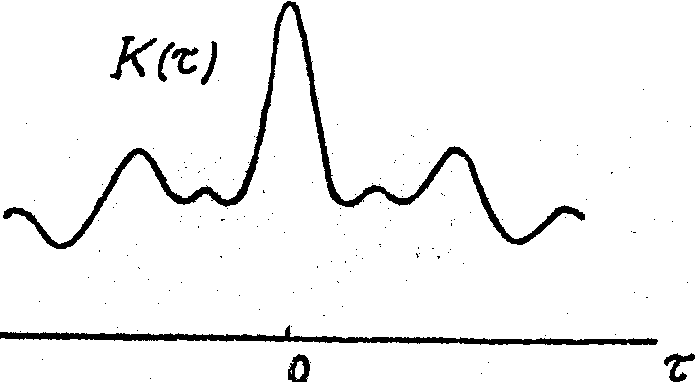
Нам встречались случаи удачного восстановления и для много импульсных функций (см.рис.5). Однако такие случаи, по-видимому, следует воспринимать как исключительные. Здесь положение такое же, как в случае восстановления пространственных функций одних только данных об автокорреляции в общем случае недостаточно для однозначного восстановления /16/. Условие неотрицательности, т.е. условие I(t) ³ 0, снижает степень неоднозначности, но полностью не снимает ее /15/. Так что можно говорить лишь о некоторых классах сигналов, для которых удастся проводить восстановление (число возможных решений не превосходит двух). В случае же произвольного сигнала метод корреляционных измерений нуждается в значительной модификации.

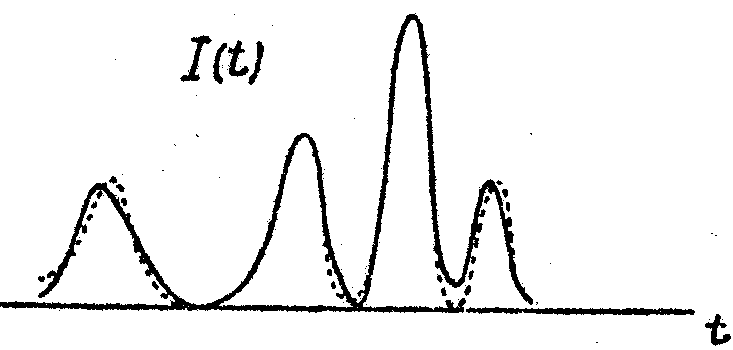
а)

б)

Рис.5. То же, что на рис.3, но исходная временная картина является многоимпульсной.

Один вариант модифицированных измерений йог бы состоять в использовании для воздействия на нелинейную среду опорного импульса 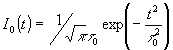. Получая при возбуждении нелинейного эффекта данные о функции корреляции опорного и сигнального импульсов (а не об автокорреляции)

K⁰(t ) = ò I₀(t)I(t + t )dt (14)

мы фактически будем записывать функцию

K⁰(t ) » I(t ) при t ₀ << t _S(15)

Однако такой вариант, по существу, примыкает к голографическим методам, а не к альтернативным. Если же вернуться к обсуждению безопорных методов, то тут следует остановиться на одной гипотетической схеме, которая основывается на идеях об экспоненциальной фильтрации. Отметим, что возможности метода экспоненциальной фильтрации применительно к пространственным задачам описаны в литературе /16/. Здесь мы применим близкий подход к временным задачам.

Допустим, на исходное излучение I(t) воздействует экспоненциальный фильтр, в результате чего создается излучение с временным ходом Ig (t):

Ig (t) = I(t)exp[-g t] (16)

Автокорреляционная функция должна регистрироваться в двух каналах: в одной - функция K(t ) для исходного излучения I(t) и в другом - функция Kg (t), соответствующая преобразованному излучению Ig (t),

Kg (t ) = ò Ig (t)I(t + t )dt (17)

Данных по этим двум функциям оказывается достаточно для восстановления временного хода интенсивности. Рассмотрим случай малых g . Следует отметить, что такой случай (g ® 0) для пространственных задач был впервые проанализирован в /17/. Введем обозначение 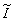(W ) для Фурье-образа интенсивности,

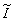(W ) = ò I(t)exp[-iW t]dt (18)

и выделим о Фурье-образе фазовый множитель и модуль

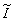(W ) = | I(W )| exp[-ij (W )] (19)

Из (13) и (17) получаем:

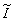| (W )| = [ò K(t )exp[-iW t ]dt ]^½ (20)

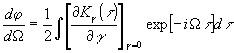(21)

Таким образом, мы видим, что па функций К(t ) и Кg (t ) можно получить полную информацию о Фурье-образе интенсивности, т.е. и о временном ходе I(t).

В данной статье мы привели перечень некоторых, не вполне традиционных, методов измерения временных характеристик излучения. В первую группу мы включили голографические методы, т.е. методы, основанные на использовании опорной волны со специально сформированными временными характеристиками (опорного импульса). Во вторую группу отнесли так называемые косвенные методы, а именно методы, сводящиеся к регистрации корреляционных функций с помощью нелинейных сред. Косвенные методы возникли раньше, более просты для реализации и экспериментально более продвинуты, чем голографические методы. Однако применение косвенных методов требует привлечения априорной информации о временных характеристиках. Установлено, что при наличии необходимой априорной информации целесообразным является применение итерационных алгоритмов для обработки данных, полученных с помощью косвенных методов.

Литература

1. Зубов В.А.. Крайсккй А.В., Кузнецова Т.И. Письма в ЖЭТФ, 1971, 13, 443.

2. Зубов В.А., Кузнецова Т.И. Квантовая электроника, 1973, № 3 (15), 135.

3. Кузнецова Т.И. //Тр. ФИАН, М., Наука, 1975, т.84, 62.

4. Borkova V.N., Zubov V.A., Kraisky A.V. SPIE. 1586, 673, 100.

5. Мазуренко В.Т. Оптика и спектроскопия, 1984, 56, 583.

6. Зуйков В.А., Самарцев В.В., Усманов Р.Г. Письма в ЖЭТФ, 1980, 32, 293.

7. Ребане А. К., Каарли Р.К., Саари П. К. Письма в ЖЭТФ, 1983, 38, 320.

8. Аbrаmsоn N. Appl.Optica, 1983, 22, 215.

9. Abramson N. Appl.Optica, 1987, 26, 4657.

10. Armstrong J.A. Appl.Phys.Lett., 1967, 10, 16.

11. Giordmaine J.A., Rentzepia P.M., Shapiro S.L., Wecht K.W. Appl.Phys.Lett., 11, 216, 1967.

12. Giuzalian R.N., Sogomonian S.B., Horvath Z.Gy. Optics Commun., 1979, 29, 239.

13. Salin F., Georges P., Roger G., Brun A. Appl.Optics, 1987, 26, 4528.

14. Fienup J.R. Optics Lett., 1978, 3, 27.

15. Fienup J.R. J.Opt.Soc.Amer. Ser.A, 1986, 3, 284.

16. Ферверда Х.А. //"Обратные задачи в оптике", ред.Г.П.Болтс, М., Машиностроение, 1964, с.21-47.

17. Абрамочкин Е.Г., Волостников В.Г., Котляр В.В., Малов А.Н. Краткие сообщения по физике в ФИАН, 1967, № 3, с.7.