ПОВЫШЕНИЕ KAЧЕCTBA РАЗНОСТНОГО ИЗОБРАЖЕНИЯ ПУТЕМ ИСПОЛЬЗОВАНИЯ KOМБИHИРОBAHHОГО ФАЗОВОГО СДВИГА
С.Н.Малоа, И.Р.Михайлова, И.С.Клименко
Метода голографического вычитания изображений путем регистрации и пространственной фильтрами в Фурье-плоскости оптической системы не находят широкого распространения ввиду того, что сравниваемые изображения формируются в выходной плоскости оптического процессора смещенными друг относительно друга. Использование комбинированного фазового сдвига при определенных условиях способствует снятию этого ограничения.
Известный способ голографического вычитания изображений /1,2/ предусматривает введение между сравниваемыми волновыми фронтами линейного фазового сдвига, что обуславливает взаимное смещение идентичных точек сравниваемых изображений в выходной плоскости оптического процессора и, как следствие, их неполное взаимное погашение.
Очевидный практический интерес представляет ситуация, при которой сравниваемые (вычитаемые) транспаранты имеют как продольное, так и поперечное взаимные смещения, т.е. одновременно реализуется линейный и квадратичный фазовые сдвиги /З/. Действительно, в схеме вычитания практически всегда взаимное смещение является комбинированным.
Исходя из вышесказанного, рассмотрим процесс вычитания изображений на основе комбинированного фазового сдвига и определим преимущества способа по сравнению с ситуациями, когда реализуется чисто линейный или квадратичный фазовые сдвиги.
Схематически процесс вычитания изображений на основе комбинированного фазового сдвига изображен на рис.1, где слева от плоскости пространственных частот (голограммы) - схема регистрации,
справа - схема восстановления разностного изображения. Опорный и восстанавливающий пучки не показаны. Предметная плоскость освещается плоской волной через диффузор с функцией рассеяния
h, который располагается в непосредственной близости от сравниваемых транспарантов t1 и t2. Для упрощения на рис.1 практически рассматривается импульсный отклик системы регистрации-восстановления. Амплитуду освещающей волны выберем равной единице. Распределение амплитуд в плоскости регистрации, соответствующее первой экспозиции, запишем следующим образом:
U1(x
) = T1(x
)Ä
H(x
) (1)
где x
= xƒ/l
ƒ, xƒ - координата в плоскости регистрации, l
- длина волны используемого излучения, ƒ - фокусное расстояние линзы, Т1(
x
) и Н(x
) - Фурье-образы функций t1(x) и h(x), соответственно. Выражение для опорной волны не записываем, поскольку при восстановлении изображения будет применяться ее копия.
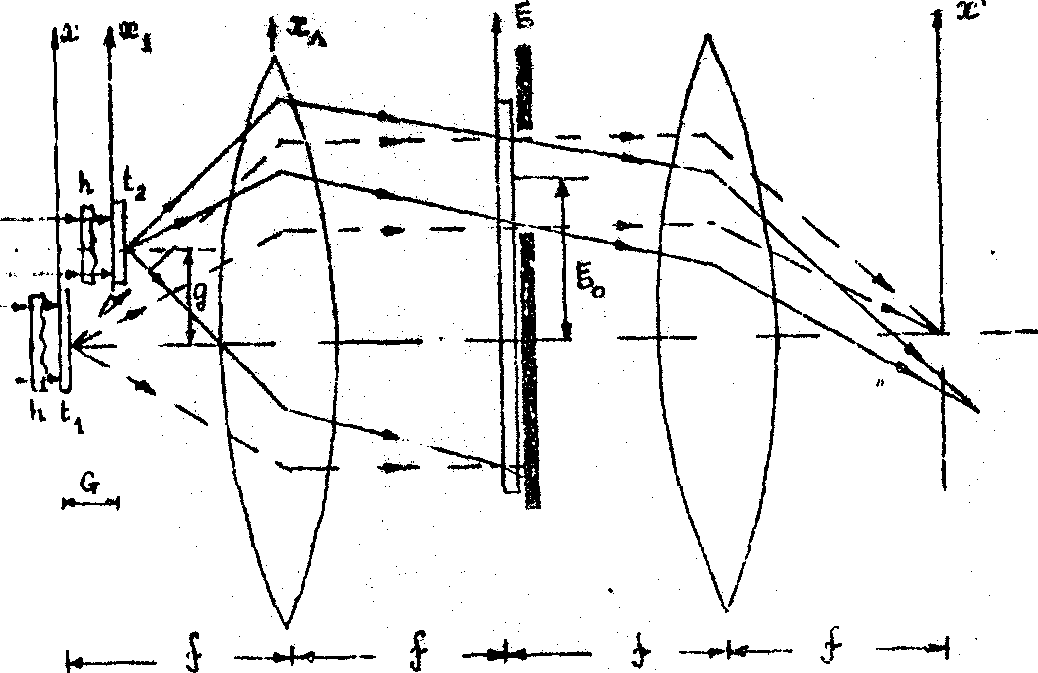
Рис.1. Голографическое вычитание изображений путем введения комбинированного фазового сдвига.
Перед второй экспозицией сравнивавши транспарант с пропусканием t
2(x
1), отстоящий на расстоянии ƒ-G (см.рис.1) от линзы, сдвинем в собственной плоскости на величину g от оптической оси системы. На выходе транспаранта получим поле.
U2(x1) = [t2(x1)h(x1)]Ä
d
(x1,d
) (2)
где свертка с дельта-функцией символизирует сдвиг транспаранта. В плоскости регистрации распределение амплитуд представим следующим образом:
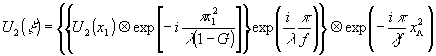(3)
где xL
- координата в плоскости линзы. Свертка входной функции U
2(x
1) c квадратичной экспонентой описывает поле, падающее на линзу, влияние которой впоследствии учитывается произведением на множитель сферической волны.
В интегральной форме выражение (3) представим в виде
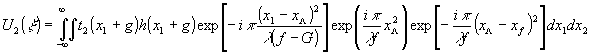(4)
где х
ƒ =
l
ƒx
. Проводя интегральные преобразования Фурье, получим
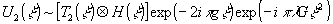(5)
где T
2(
x
) - Фурье-образ функции t2(x1). Выражение (5) свидетельствует о том, что волна, несущая Фурье-образ входной функции, распространяется под углом к оптической оси j
~g/ƒ, а также приобретает сферичность за счет выхода транспаранта t2(x)
из передней фокальной плоскости линзы на величину G (рис.1).
При восстановлении изображений копией опорного пучка на выходе голограммы получим поле
UB(x
) ~ T1(x
)Ä
H(x
) + [T2(x
)Ä
H(x
)]exp(-2ip
gx
)exp(-ip
l
Gx
2) (6)
Последнее выражение описывает только часть реконструируемого голограммой поля. Опущенные слагаемые, представляющие волны, распространяющиеся под существенно большими углами, интереса в данном случае не представляют, поскольку последующая пространственной фильтрации их блокирует. Кроме того, в (6) опущены постоянный коэффициенты, связанные с влиянием фотохимического процесса проявления на пропускание регистрирующего слоя.
Представим отличие между сравниваемыми транспарантами в виде функции разности
t0(x) = t2(x) – t2(x) (7)
которую подставим в выражение (6):
UB(x
)=[T1(x
)Ä
H(x
)][1+exp(-2ip
gx
)exp(-ip
l
Gx
2)] + [T0(x
)Ä
H(x
)]exp(-2ip
gx
)exp(-ip
l
Gx
2)(8)
где Т
0(х) - Фурье-образ функции разности t0x. Заметим, что само задание разностной функции в виде (7) обуславливает взаимную раскорреляцию волн, описываемых первым и вторым слагаемыми выражения (8). Поэтому представим наблюдаемое распределение интенсивности в плоскости голограммы. как сумму квадратов модулей первого и второго слагаемых выражения (8):
I(x
) = 4|
T1(x
)Ä
H(x
)|
2Cos2[p
(l
Gx
+ 2g)x
/2] + |
T0(x
)Ä
H(x
)|
2 (9)
Выражение (9) свидетельствует о том, что в плоскости голограммы интенсивность Фурье-образа идентичной части в сравниваемых
изображениях оказывается промодулированной квадратичным косинусоидальным множителем. На это поле квазинепрерывным образом накладывается интенсивность Фурье-образа разностной части, снижая тем самым видность интерференционной картины. Схематически нормированное распределение интенсивности в плоскости голограммы при конкретных значениях параметров оптической системы представлено на рис.2, где
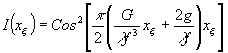
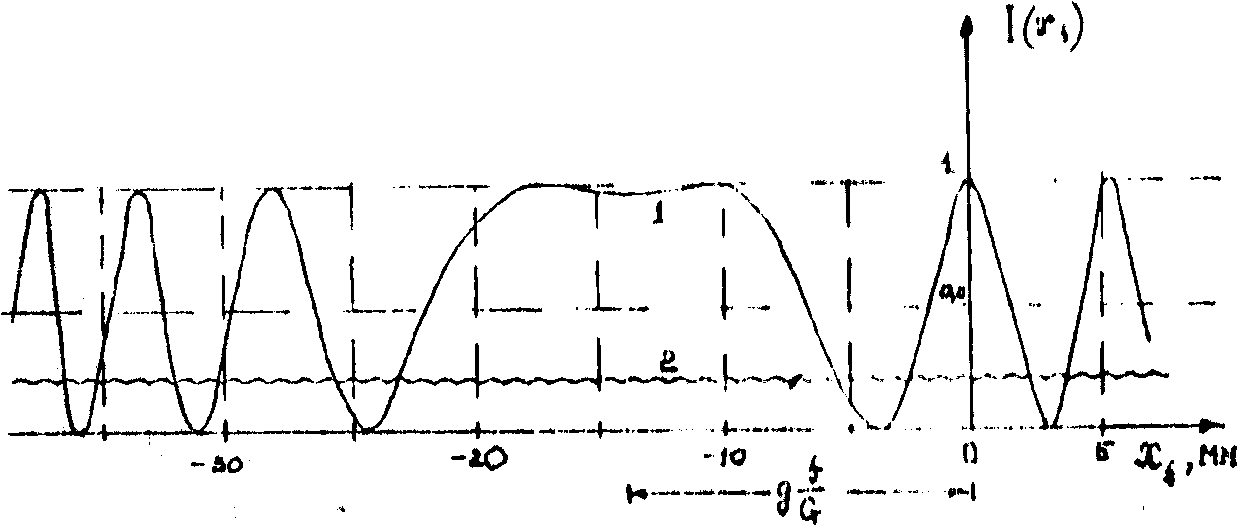
Рис.2. Кривая 1 - интенсивность Фурье-образа идентичной части (первое слагаемое (9)), кривая 2 - интенсивность Фурье-образа разностной части. Кривая 1 построена при
g = -20 мкм, G = 300 мкм, l
= 0,63 мкм, ƒ = 210 мм.
Нули косинусоидальной функции (центры интерференционных минимумов) соответствуют значениям пространственных частот;
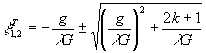, k = 0,1,2 … (10)
а максимальные значения (центры интерференционных максимумов) функция принимает в точках:
, 
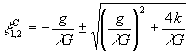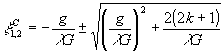(11)
Двумерный анализ этого процесса показывает, что в плоскости голограммы формируется концентрическая система интерференционных колец, локальный период которых убывает к периферии голограммы. Как видно из рис.2, картона симметрична и центр симметрии смещен относительно оптической оси на расстоянии
gƒ/G, причем знак этого смещения совпадает со знаком g.
На кривой 1 (рис.2) в центре концентрической системы колец может существовать провал, где значение косинуса при выполнении условия
g2 = l
G(2k + 1), k = 0,1,2 ... (12)
обращается в нуль. На рис.3 приводится схематическое нормированное распределение интенсивности в плоскости голограммы при выполнении условия (12). Видно, что в центре симметричной системы интерференционных колец формируется относительно широкий провал, пригодный для проведения пространственной фильтрации с целью определения разницы между входными изображениями.
Определим ширину этого интерференционного минимума L как половину расстояния между соседними с ним максимумами, положение которых описывается формулами (11):
(13)
Последнее выражение показывает, что ширина центрального интерференционного минимума находится в обратной зависимости от продольного смещения одного из сравниваемых транспарантов. Очевидно, что максимальный размер L имеет место при устремлении G к нулю, однако, в этом случае расстояние от центра колец до начала координат (
gƒ/G) становится бесконечно велико, что соответствует чисто поперечному взаимному смещению сравниваемых транспарантов (линейный фазовый сдвиг). С другой стороны, при g = 0 и G¹
0 условие (12) выполняться не может и значение
функции
Cos2(-xg2/2l
G) обращается в центре концентрических колец в +1, а центр, в свою очередь, совмещается и началом координат, что реализуется при впадении квадратичного фазового сдвига между сравниваемыми волновыми фронтами.
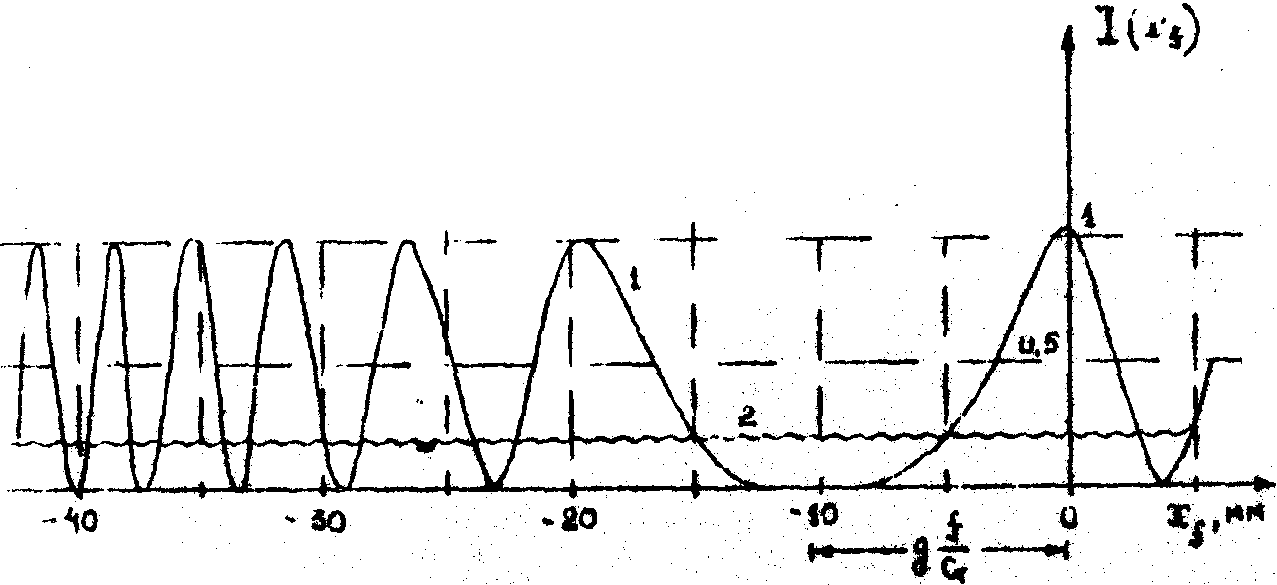
Рис.3. Кривая 1 - интенсивность Фурье-образа идентичной части при k= 0,
g =-13,75 мкм, G = 300 мкм, l
= 0,63 мкм, ƒ = 210 мм. Кривая 2 - интенсивность Фурье-образа разностной части.
Пространственную фиьтрацш воля (В) будем осуществлять фильтром с пропусканием
rect[(x
- x
0)/c], где с = 2r/l
ƒ, r - радиус фильтрующего отверстия, x
- положение центра отверстия (рис.1). Представим поле на выходе фильтра в виде трех слагаемых:
UB(x
) = W1(x
) + W2(x
) + W3(x
) (14)
где
W1(x
) = [T1(x
)Ä
H(x
)]rect[(x
- x
0)/c]
W2(x
) = [T1(x
)Ä
H(x
)]rect[(x
- x
0)/c]exp(2ip
gx
)exp(-ip
l
Gx
2) (15)
W3(x
) = [T0(x
)Ä
H(x
)]rect[(x
- x
0)/c]exp(2ip
gx
)exp(-ip
l
Gx
2) (16)
Распределение амплитуд. создаваемое волной (14) в плоскости наблюдения, описывается выражением
W1(x') = [t1(x')Ä
h(x')]Ä
Sinc(p
cx')exp(-2ip
x
0x') (17)
которое свидетельствует о наклоне волны, несущей изображение идентичной части сравниваемых транспарантов, а также об уширении каждой точки изображения.
Поле в плоскости х', создаваемое волной (15), представим также в виде обратного Фурье-преобразования:
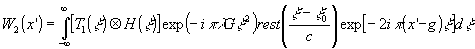(18)
Для вычисления последнего интеграла произведем в подынтегральном выражении некоторые преобразования, которые приведут к виду:
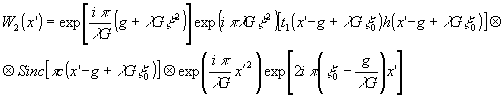(19)
Пусть центр фильтрующего отверстия совпадает с центром интерференционного минимума, т.е. x
0 = g/
l
G
, тогда для (20) имеем
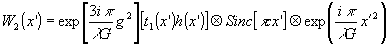(20)
При этом же условии фильтрации выражение (17) примет вид:
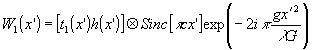(21)
где мы можем опустить экспоненциальный множитель благодаря тому, что
g<<G, т.е. поле, формирующее изображение идентичной части транспарантов, распространяется практически параллельно оптической оси. В выражении (20), потребовав выполнения условия малости радиуса фильтрующей апертуры, можно пренебречь последним квадратичным экспоненциальным множителем, описывающим расфокусировку изображения вследствие выхода одного из транспарантов из передней фокальной плоскости линзы.
После этих упрощений запишем суммарное пале, образованное амплитудным сложением двух волн, описываемых (20) и (21), и виде
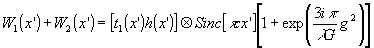(22)
что свидетельствует об интерференционном взаимодействие двух идентичных полей с комбинированным фазовым сдвигом. Распределение интенсивности, создаваемое поляки (22), будет
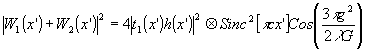(23)
Поскольку при регистрации было выполнено условна (12), обращающее последнее выражение в нуль, то распределение интенсивности в выходной плоскости получим в виде разницы между входными изображениями (после проведения обратного Фурье-преобразования выражения (16)):
IB(x') = |
t0(x')h(x')|
2Ä
Sinc2(p
cx) (24)
Существенно, что если в известном способе вычитания /1,2/ принципиально невозможно получить высокое отношение сигнал/шyм разностного изображения в силу относительного смещения идентичных
точек в выходной плоскости, то в описываемом методе такая возможность существует и реализуется, как показывает приведенный выше анализ, при выполнении условия (12) и пространственной фильтрации путем освещения нерасширенным лазерным пучком области голограммы, соответствующей центру симметрии кольцеобразной интерференционной структуры. Это обуславливает формирование в выходной плоскости несдвинутых друг относительно друга противофазных изображений идентичных точек сравниваемых объектов, что и приводит к существенному повышению отношения сигнал/шум разностной картины.
На основе применения представленного здесь голографического метода вычитания изображений может быть решена проблема очувствления автоматических манипуляторов, предназначенных для автоматизации процессов отбраковки изделий при крупносерийном их производстве путем сравнения сединой детали с эталоном. Очевидно, что подобньй процесс необходимо организовывать в реальном масштабе времени /4/.
Литература
1. Клименко И.C., Малов С.Н., Рябухо В.П. Голографическое вычитание изображений на основе пространственной фильтрации узким пучком, // Доклады АН СССР. - 1983. - Т.272. № 2. - с.365-369.
2. Клименко И.C., Малов С.Н., Рябухо В.П. Голографическое вычитание изображений на основе регистрации и пространственной фильтрация в Фурье-плоскости. // Физические основы и прикладные вопросы голографии / (Тематический сборник, - Л.: ЛИЯФ. - 1984. - с.74-101.
3. Малов С.Н., Клименко И.С., Вычитание изображений с использованием комбинированного фазового сдвига. // Тез.докл. Пятая Всесоюзная конференция по голографии. Часть 2. Рига. – 1985. - с.299-300.
4. Малов С.И. Вычитание изображений в реальном масштабе времени. // Применение методов голографии в науке и технике. /Сборник научных трудов. - Л.: ЛФТИ. - 1987. - с.34-39.
