ОБОБЩЁННЫЕ ФУНКЦИИ И

ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ДЛЯ ОПТИКОВ

Л.М.Сороко

Поясним принципиальное различие между голографией и фотографией. Поставим вопрос так: что является предметом регистрации в фотографии и в голографии?

Предметом наблюдения в фотографии является картина почернения на негативе или позитиве, которая по своему информационному содержанию является образом предмета, полученным с помощью операции центрального проектирования элементов предмета на плоскость фотоэмульсии. Чтобы "точка" изображения была чёткой, необходимо, чтобы соответствующая точка предмета попала в зону резкости. В противном случав точка изображения размывается. Информационная ценность размытых частей изображения сильно ослабевает.

Операция центрального проектирования - это точечно-точечное преобразование. Каждой точке предмета, находящейся в зоне резкости, отвечает только одна точка изображения. Эта операция не является взаимно однозначной. Две точки предмета, лежащие на одном и том же проецирующем луче, дают одну и ту же точку изображения. Такая неоднозначность в фотографии не позволяет, например, по проекционному образу предмета установить объёмные очертания предмета или сцены. Абсолютно невыполнимой оказывается даже самая простая задача: регистрация мельчайших пылинок в пространстве. Фотонегатив пылинок даёт экспериментатору информацию только о направлении луча света, отражённого от капельки и проходящего через центр проекции, который лежит на оптической оси. Сведений о дальности до капельки фстонегатив не содержит. Поэтому операция центрального проектирования элементов объёмной сцены на плоскость относится к классу необратимых преобразований. Чтобы из-

 

бавиться от такой неоднозначности, используют два фотонегатива, сделанных с различных точек съёмки. По двум проекциям можно определить дальность до каждой точки предмета.

В противоположность фотографии предметом регистрации в голографии является само волновое поле. Более точно - стационарное квазимонохроматическое волновое поле, созданное вблизи голограммы несамосветящимся предметом. Это волновое поле состоит из совокупности элементарных волновых полей, идущих от каждой точки предмета. В области голограммы оно имеет сложную пространственную структуру.

Задача голографии состоит в том, чтобы как модно полнее зарегистрировать пространственную структуру поля в некоторой выбранной части пространства иди хотя бы в одной плоскости. Волновое поле в плоскости характеризуется в общем случае двумя функциями: распределением амплитуды и распределением фазы или такими параметрами, как кривизна волнового фронта и яркость излучения в каждой точке. Так или иначе, регистрируемое волновое поле характеризуется двумя функциями и их надо однозначно и раздельно зарегистрировать. Однако известно, что фотоэмульсия независимо от того, где она используется, в фотографии или в голографии, способна зарегистрировать только одну функцию. Это - распределение почернения негатива, отображающее распределение интенсивности света в плоскости фотоэмульсии.

Для того, чтобы фотоэмульсия могла вобрать в себя одновременно две функции, необходимо воспользоваться услугами опорного пучка. Опорный пучок, являющийся как бы "напарником" фотоэмульсии, имеет, как правило, простую и легко воспроизводимую пространственную структуру. Это - либо коллимированный пучок, либо сферическая волна. Опорный пучок является репером, относительно которого сравнивают обе функции, подлежащие регистрации, а именно: амплитуду и фазу.

Для этого используют явление интерференции света, которое разыгрывается в области пересечения предметного и опорного пучков. При этом вариации амплитуды предметного пучка записываются в форме вариации контраста интерференционной картины, а вариации

фазы создают сдвиги интерференционных полос, что приводит к их сгущению и разряжению.

Так достигается полнота и расчленённость записи инфориации о волновом фронте. Другой важной особенностью голографичесного метода является то, что регистрируемая с помощью интерференционной картины информация может быть обратимо извлечена из голограммы на стадии восстановления. Здесь используется явление дифракции света, благодаря которому процесс декодирования осуществляется как бы автоматически.

Голография и интегральные преобразования. Цепочку преобразований, которые используются в голографии, можно изобразить следуюцей схемой (рис.1).

---

 

 

Рис. 1.

Эти преобразования по своей природе являются интегральными. Действительно, каждая точка голограммы воспринимает сразу информацию от многих точек предмета или транспаранта. Рассматриваемые здесь интегральные преобразования так же, как и сами процессы в голографии, являются обратимыми. Исходная функция, которая реги-

стрируется на голограмме, является комплекснозначной, т.е. состоит из упорядоченной пары функций, например, действительной и мнимой частей или амплитуды и фазы и т.д.

Скажем несколько слов о некоторых других системах преобразования исходного сигнала. Рассмотрим шифрование и кодирование.

Фотографирование является примером самого простейшего кодирования, осуществляемого с помощью центрального проектирования. Здесь образ в точности совпадает с тем, что имеется на плоском транспаранте. Это позволяет человеку визуально воспринимать информацию, содержащуюся в этом образе, и непосредственно ощущать смысл исходной информации.

Точечно-точечное кодирование плоского транспаранта по любой произвольной программе можно осуществить методами волоконной оптики с помощью связки переплетённых светопроводящих волокон. Такое точечно-точечное кодирование является обратимым. На стадии обработки непонятную для глаза преобразованную информацию можно расшифровать и увидеть исходную картину или текст.

В чём состоит различие между системой кодирования с помощью олоконной оптики и теми интегральными преобразованиями, которые реализуются в когерентных оптических системах? Во-первых, кодирование и декодирование в волоконной оптике осуществляется с помощью уникального кодировщика. Если мы потеряем этот кодировщик, либо схему переплетения волокон, то ни одну из этих стадий, в четности декодирования, мы осуществить не сможем. Во-вторых, волоконный кодировщик невозможно сделать пространственно инвариантным. Если кодировщик смещён относительно зашифрованной записи, то исходное изображение уже не восстановится.

В противоположность этому в голографии осуществляются такие операции, которые, как правило, являются пространственно инвариантными, а стадия восстановления осуществляется естественным процессом дифракции света, т.е. как бы автоматически. Включение голографического декодировщика происходит одновременно с включением лазерного пучка. Это очень важное и ценное достоинство голографических операций, природа которых описывается в первом приближении оптическими интегральными преобразованиями, которые будут кратко рассмотрены в данной лекции.

Степень обратимости и фактор надёжности реальных процессов в голографии находятся в сильной зависимости от ряда факторов, в частности уровня шумов. Большое значение имеют также коэффициент заполнения полосы пропускания, быстрота выполнения голографических стадий, разрешающая способность и другие. Эти факторы здесь рассматриваться не будут.

В лекции будут освещены следующие вопросы: краткая теория обобщённых функций, преобразование Фурье обобщённых функций, интегральные преобразования типа свертки, линейный фильтр преобразования Френеля, обратная задача свертки - деконволюция, разрешающая способность прибора с учётом шумов в задаче разрешения тесного дублета, шумоподобная модуляция и демодуляция, а также поучительные примеры: превращение фазового контраста в контраст интенсивности с помощью фазовой пластины, ножа Фуко и преобразования Гильберта. Все эти вопросы имеют непосредственное отношение к анализу голографических систем, оптических согласованных фильтров, пространственно инвариантных трансляторов и других когерентных систем. Как правило, во всех таких системах регистрируемый сигнал является некоторым интегральным образом исходного сигнала.

Прежде чем перейти к рассмотрению математического аппарата и соотношений, которые реализуются в когерентных оптических системах, познакомимся кратко с так называемыми обобщёнными функциями .

Обобщённая функция. Теория обобщённых функций - это операционный формализм, сводка алгоритмов и правил, которые позволяют понять и количественно проанализировать многие задачи, встречающиеся в голографии и оптической обработки информации. Термин "операционный" здесь означает, что доказательства существования и однозначности в этой теории полностью опущены. Излагаются только одни алгоритмы. Доказательство алгоритмов - дело математиков. Все вопросы, которые обсуждаются в этой лекции, имеют прочный фундамент в виде строгих математических обоснований, полученных несколькими совершенно различными подходами. Это позволяет утверждать, что операционный формализм обобщённых функций является замкнутой теорией в такой же степени, как и операционный фор-

мализм, развитый когда-то для анализа процессов в электрических цепях. В настоящее время этот операционный формализм обобщён на случай двухмерных и трёхмерных систем и продолжает в настоящее время обобщаться дальше на случаи систем с частично когерентным смещением.

История обобщённых функций восходит к концу прошлого века, когда Хэвисайд ввёл систему символических правил для анализа процессов в электрических целях. Ему пришлось ввести так называемую функцию включения. Этим было положено начало операционному исчислению. Позднее физик Дирак ввёл ещё одну новую функцию, названную его именем. Были определены также правила диференцирования дельта-функции Дирака и функции Хэвисайда. Ещё позже математики нашли строгое обоснование операционному исчислению Хэвисайда-Дирака.

Функции, введённые Хэвисайдом и Дираком, а также многие другие необычные функции, были названы обобщёнными функциями. В основе теории обобщённых функций лежит правило обоощения функции и новое определение самой функции.

Определить обобщённую функцию - это значит определить правило, согласно которому любой функции g(x) из класса "хороших" функций приписывается некоторое число. Это число является продуктом интегрального воздействия данной обобщённой функции на выбранную нами хорошую функцию.

"Хорошей" функцией называется такая функция, которая не имеет сингулярностей, бесконечно дифференцируема и финитна, т.е. отлична от нуля только в конечной области задания.

Понятие обобщённой функции в такой мнемонической форме с помощью алгоритма удаётся ввести благодаря тому, что обобщённые функции никогда не входят непосредственно в результаты измерений. Они всегда фигурируют под знаком интеграла, описывающего стадию наблюдения иди регистрации. Поэтому достаточно знать только результат действия данной обобщённой функции, не затрагивая деликатный вопрос о тем, как её точно и строго определить. То, что при таком алгоритмическом подходе не возникает неоднозначностей, доказано строго математиками.

Дельта-функция Дирака. Её физический аналогом может служить бесконечно малое отверстие с конечной интенсивностью пропущенного света или бесконечно узкая щель.

Обобщённая функция Дирака δ(x) определяется через результат действия функции Дирака на некоторую хорошую функцию g (x),

а именно:

∫ δ(x-x₀)g(x)dx = g(x₀). (1)

Пределы интегрирования совпадают с областью задания функции, и в общем случае они опускаются.

Итак, операция действия функции Дирака на хорошую функцию δ (х) сводится к тому, что в ответе указывается значение этой функции в точке x = Х₀

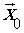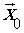Если сложить вместе точечное отверстие, находящееся в точке , с транспарантом, то свет, прошедший через такую систему, укажет нам характеристику транспаранта в точке . Таким образом, дельта-функция - это узкий единичный сигнал.

Операция, записанная в левой части (1), имеет смысл скалярного произведения. Действительно, по определению скалярное произведение двух функций f(х) и g(x) равно

∫ f(x)g(x)dx ≡ <f(x),g(x)>, (2)

где использована сокращённая запись скалярного произведения. С учётом (2) определение функции Дирака запишется так:

<δ(x-x₀),g(x)>=g(x₀). (3)

В частном случае

<δ(x),g(x)>=g(0). (4)

 

Дельта-функции могут быть одномерными и двухмерные. При этом в двухмерном пространстве дельта-функции могут быть как одномерными, так и двухмерными.

Двухмерная дельта-функция 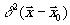, где 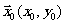точка на плоскости, изображается в виде единичной "пики'' в точке 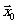. На плоскости можно ввести дельта-функцию ,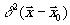

изображаемую в виде "забора'' (рис.1).

Произведение обобщённой функции f(x) на бесконечно дифференцируемую функцию а(х) также является обобщенной функцией. При этом имеет место следующее соотношение:

<a(x)f(x),g(x)>=<f(x),a(x)g(x)>. (5)

Пример. Возьмём обобщённую функцию Дирака f(x)=δ(х), а a(x)=x , тогда

 

<x δ(x), g(x)>=< δ(x), xg(x)>=[x g(x)] = 0 (6)

x=0

Отсюда в силу ограниченности g(x) на конечном интервале или финитности получаем следующее нетривиальное соотношение

x δ(x) = 0. (7)

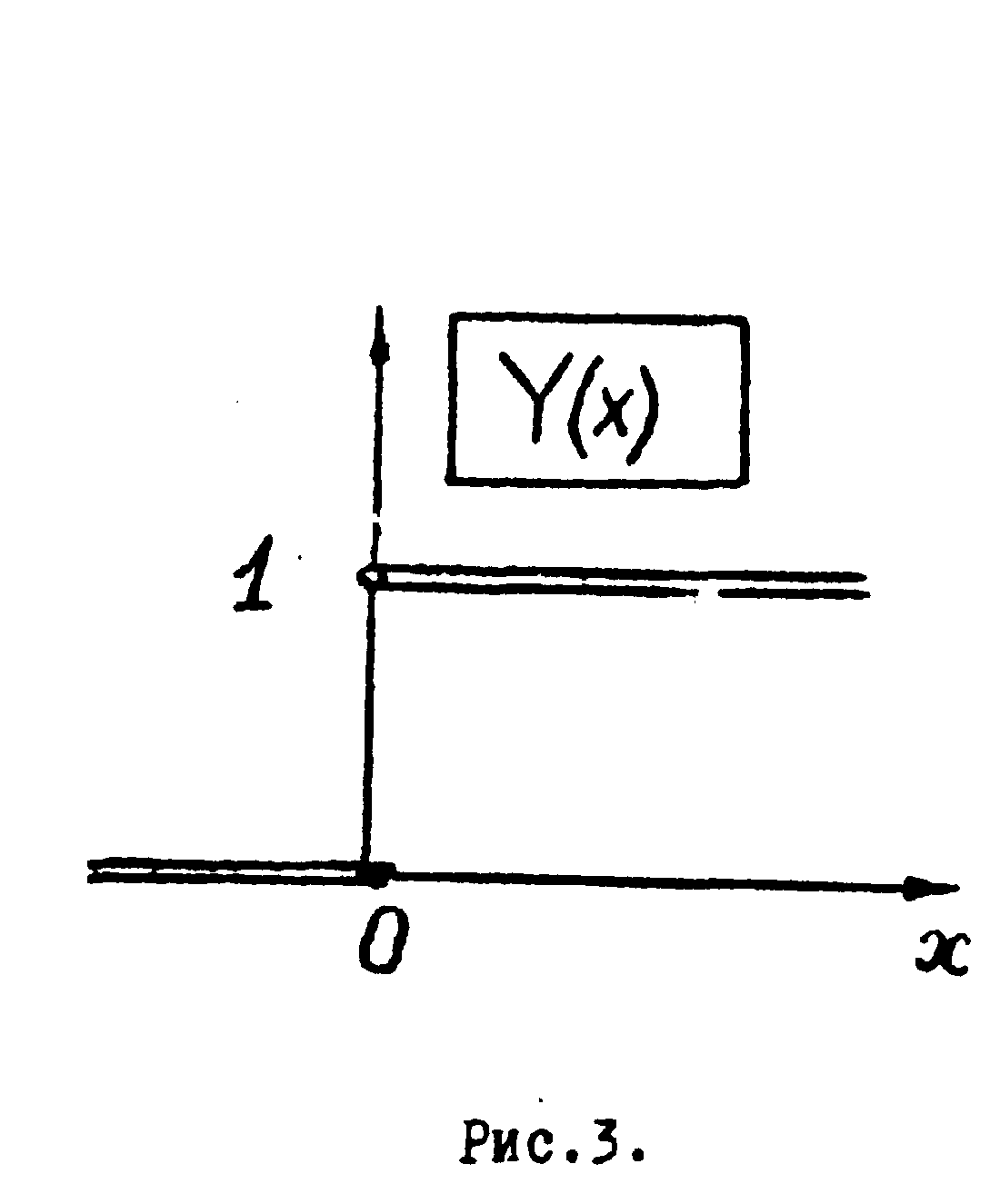
Функция Хэвисайда. Другим примером обобщённой функции является функция Хэвисайда y(х) (рис.2)

 

0, x<0

y(x)=

1, x≥0, (8)

 

которая называется единичной ступенькой или функцией включения. Дифференцирование обобщённых функций. Правило дифференцирования обобщённых функций гласит

 

 

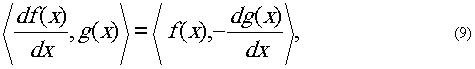
т.е. дифференцирование обобщённых функций заменяется дифференцированием хорошей функции.

Пример. Продифференцируем функцию Хэвисайда с помощью алгоритма (9). Имеем:

 

 

 

 

 

 

 

 

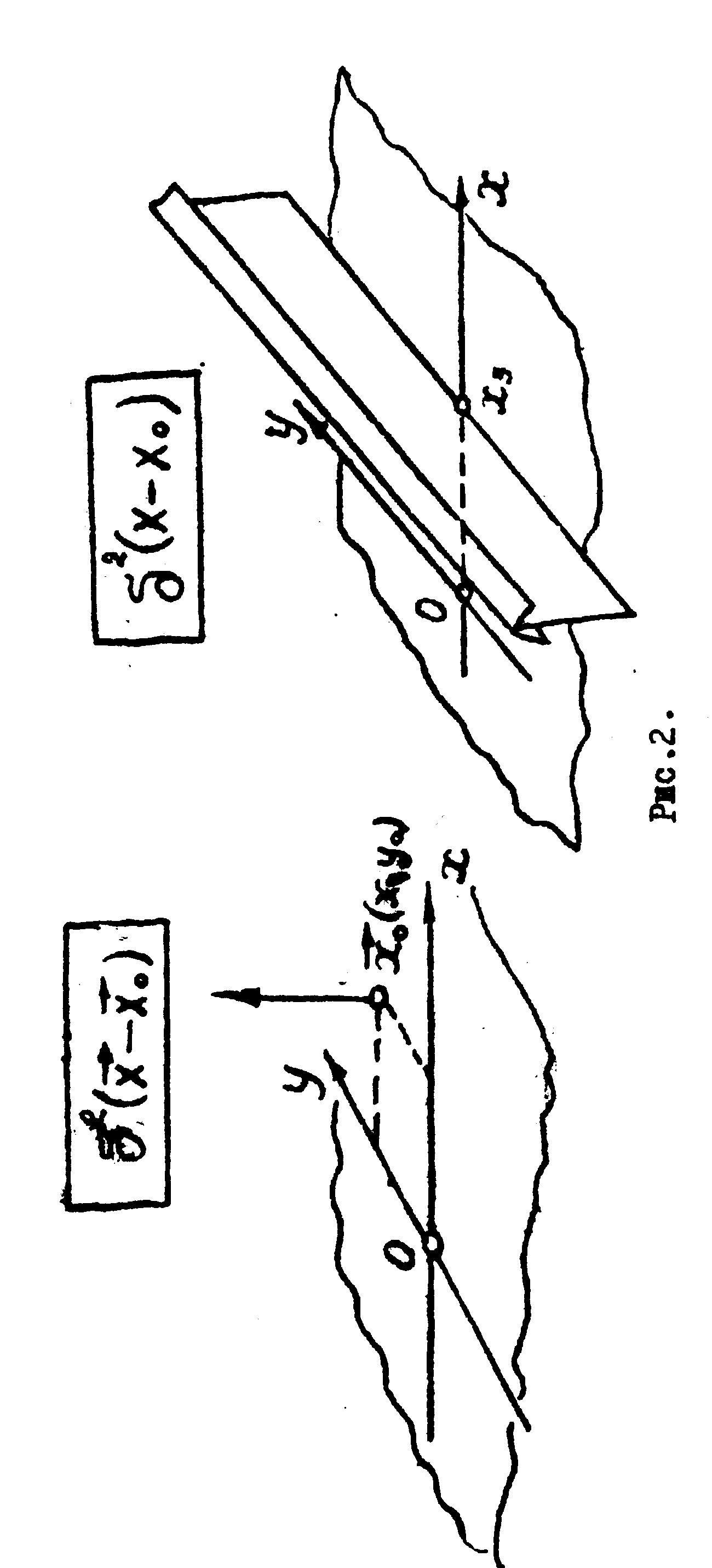
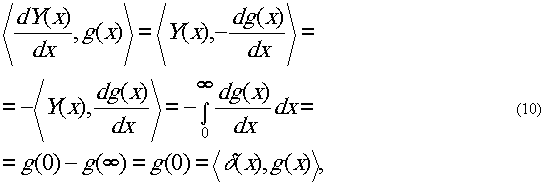
где g(∞)=0 в силу финитности хорошей функции g(x). Последний шаг этого алгоритма заключается в том, чтобы приравнять левые сомножители в двух записях, правые сомножители в которых являются одинаковыми. Из (10) находим

Пример. Обобщённая функция: главное значение 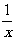или 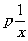. По определению

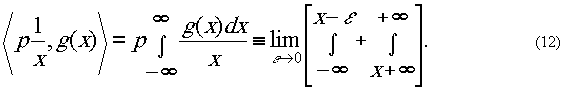
Преобразование Фурье. Преобразованием Фурье называют переход от исходной функции f(х) к Фурье-образу f(ω), который записывается так

'

Обратное преобразование Фурье - это переход от Фурье-образа f(ω) к прообразу иди к исходной функции f(x):

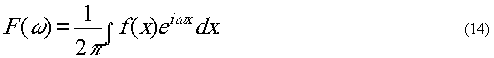
Интегрирование в (13) и (14) ведётся по области задания функций f(x) или f(ω). Таким образом, преобразование Фурье является взаимно-обратимым .

Прямое и обратное преобразование отличается знаком в экспоненте. Это имеет определённый физический смысл. Полное восстановле-

ние может быть достигнуто только тогда, когда на её стадии процесс разыгрывается строго в обратной последовательности. Если на прямой стадии пучок расходился, то на обратной стадии пучок должен сходиться. Осуществить расшифровку информации на стадии восстановления мы можем полностью только при соблюдении этого условия. Типичный пример - кодирование волнового поля с помощью матового стекла. Для того, чтобы получить с максимальной достоверностью исходную информацию, лучи света надо пустить обратно через матовое стекло. Переход от прямого процесса к обратной его последовательности математически выражается операцией комплексного сопряжения.

Теорема о переносе. Если совершить переход от исходной функции f(x) к функции, которая получена из функции f(x) путём её сдвига на величину х₀ то Фурье-образ новой функции равен

где f(ω) - Фурье-образ функции f(x). Обратно

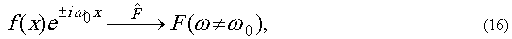
где значок 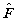обозначает прямое преобразование Фурье. Таким образом, сдвигу исходной функции соответствует операция умножения на фазовый множитель в координатах Фурье. Модуль или распределение интенсивности при этом не меняется. В этом и состоит инвариантности картины Фурье-образа относительно поступательных перемещений исходного сигнала в кадре когерентной оптической системы.

Правила дифференцирования. Если существуют производные, которые мы хотим вычислить, то имеют место следующие соотношения:

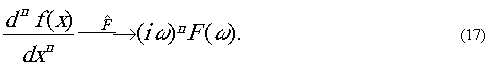
Далее, если среднее значение функции f(x) равно нулю, то

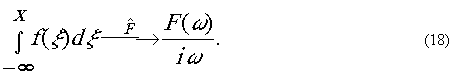
Аналогично

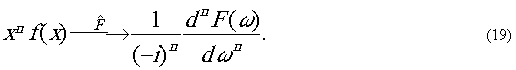
Если f (x) - действительная функция, то Фурье-образ f(x), записанный в виде

f(ω)=a(ω)e^iΦ(ω), (20)

обладает следующими свойствами:

a(ω)=a(-ω), (21)

Φ(ω)=-Φ(-ω).

Амплитуда становится чётной функцией ω, а фаза - нечётной функцией, так что всегда

Φ(0)=0. (22)

Поэтому Фурье-образ действительной функции можно задать только для положительных частот ω. Отрицательные частоты новой информации не содержат.

Пример. Найдём Фурье-образ прямоугольного импульса

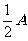, |x|<a

П_А(x)= (23)

0, |x|>a,

 

 

f(ω) - χисто действительная в силу симметричности исходной функции П_a(х).

Сдвинутый прямоугольный импульс

П_a(х-х₀) (25)

имеет Фурье-образ

 

 

Φ(ω)=-ωx_{0. (27)}

Фаза отлична от нуля в силу несимметричности.сигнала относительно .начала координат. Однако Φ(0)=0 в силу действительности исходной функции.

Преобразование Фурье обобщённых функций. Рассмотрим второй алгоритм теории обобщённых функций, который позволяет прямо находить Фурье-образ обобщённых функций. Алгоритм имеет следующий вид:

 

 

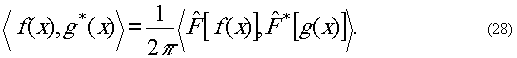
Он позволяет быстро находить ответ. Докажем, что

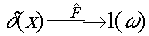(29)

Вычислки правую часть (28):

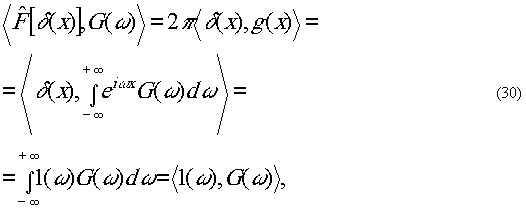
так как

e^iωx(x=0)=1(ω) (31)

 

Из равенства правых сомножителей в начале и конце выкладок находим

 

Аналогично доказывается, что

 

 

Обратно

Пример. Найдём Фурье-образ тригонометрических функций бесконочной длины. Имеем

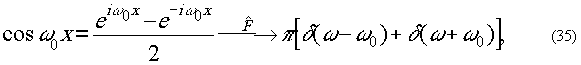
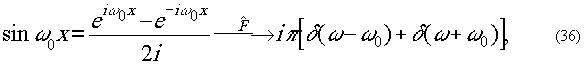
Пример. Фурье-образ функции Хэвисайда и знаковой функции

1, x>0

sgn x = , (37)

-1, x<0

sgn x = 2 y(x) - 1 (38)

Мы знаем, что из (11)

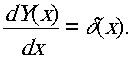
Тогда

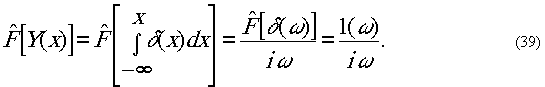
Получаем следующее исходное соотношение:

Его решением является

Функция sgn x постоянной составляющей не содержит. Поэтому с учётом (38) находим

 

 

 

 

 

 

 

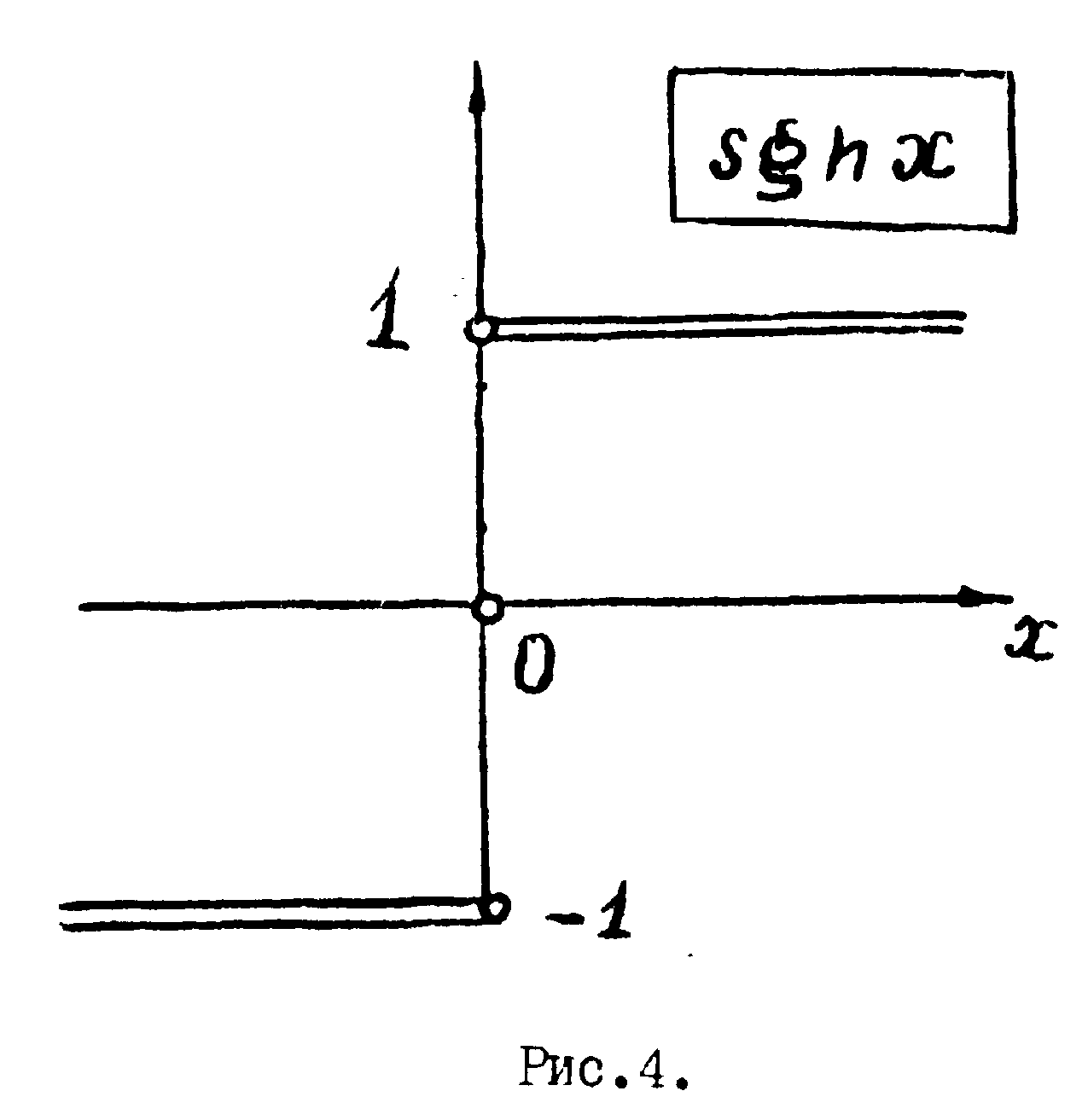
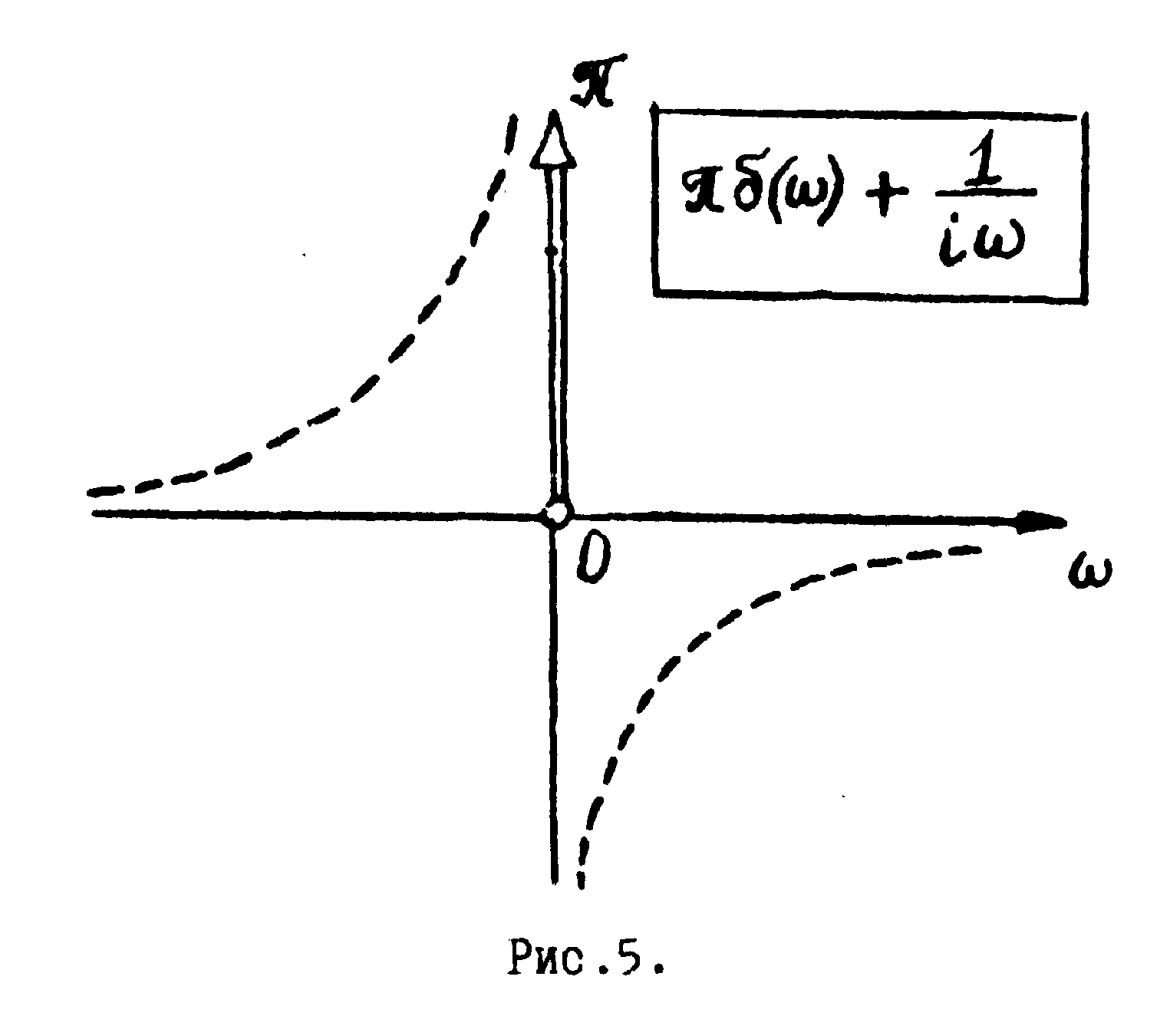
Фурье-образ функции sgn x является чисто мнимым в силу нечётности исходной функции. Фурье-образ функции Хэвисайда содержит как действительную, так и мнимую части. При этом они частотно разделены. Действительная часть сосредоточена при нулевой частоте, а мнимая -вне.

Если такой Фурье-сигнал мы попытаемся зарегистрировать голо-графически, то наибольший контраст интерференционные полосы будут иметь вблизи нулевой частоты, при высоких частотах контраст будет постепенно ослабевать. Полосы справа |ω>о| будут сдвинуты на фазу -π/2 а полосы слева (ω<0) сдвинуты на фазу +π/2 по отношению к холостой голограмме, полученной для сигнала вида 1(ω).

Пример. Найдём Фурье-образ функции

 

f(x)=|x| (43)

и выполним дифференцирование. Подчеркнём здесь, что переход от функции f₁(х)=x к функции f₂(x)=|x| приводит нас к необходимости воспользоваться аппаратом обобщённых функций. Действительно, для того, чтобы записать функции f₂(x)=|x| аналогически, нам придётся воспользоваться знаковой функцией sgn х , обращение с которой требует знания теории обобщённых функций.

Итак, рассмотрим функцию

f(x) = |x| = x*sgn x. (44)

Воспользовавшись соотношением (42), находим

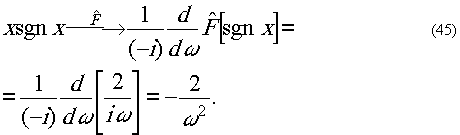
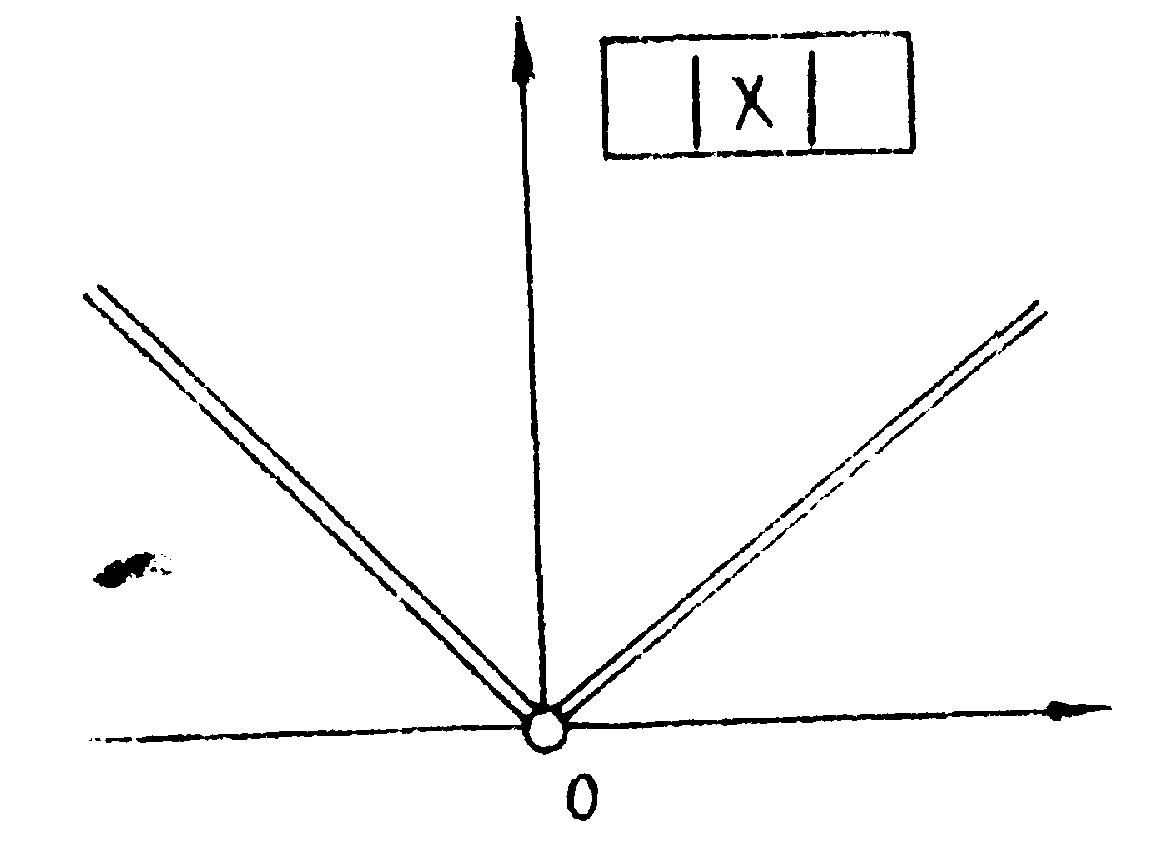
Рис.6.

 

 

 

 

 

 

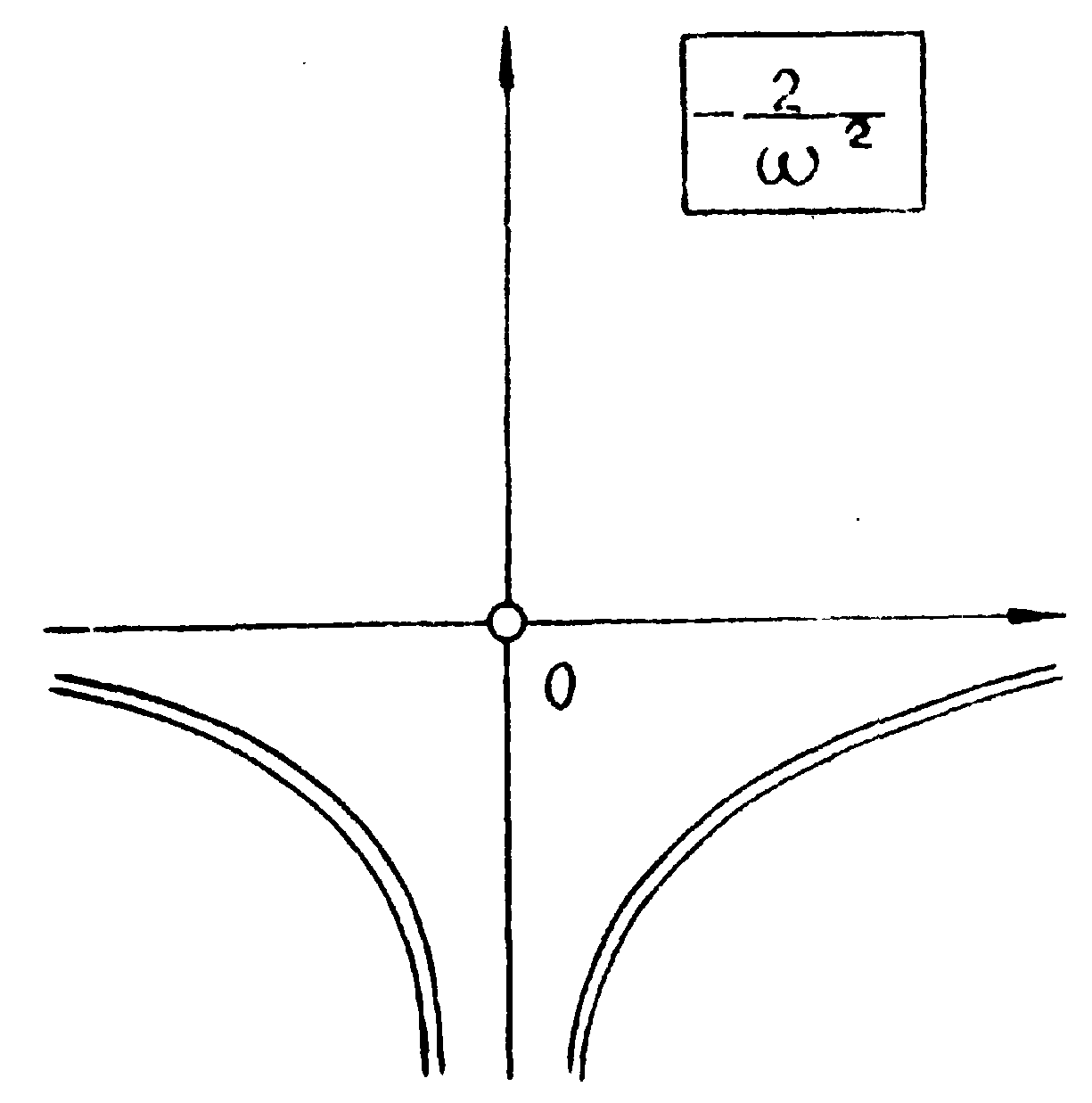
Рис.7.

 

 

 

 

 

 

 

Таким образом

Продифференцируй функцию (42) по х, получим

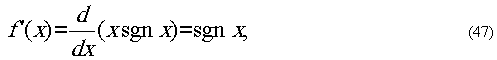
Фурье-образ которой нам известен (42). Найдём теперь вторую производную функции (44).

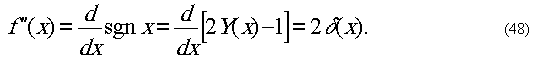
Эта функция на рисунке изображается в виде пики высотой 2. В координатах ω Фурье-образ изображается прямой

от дельта-функции Дирака отличается коэффициентом 2.

Пример. Функция, равная косинусоиде при х>о и нулю при x<0

Фурье-образ такой функции равен

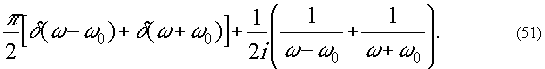
Аналогично

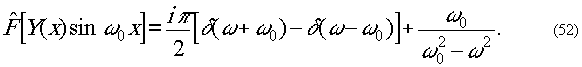
Из рис.8 видно, что введение ножа Фуко, закрывающего половину апертуры, в которую помещена симметрично относительно точки х=0 дифракционная решётка, приводит к появлению ореолов вокруг первого порядка дифракции. Если эти ореолы записать на голограмму, то появятся те же сдвиги интерференционный: полос, как и в случае функции Хэвисайда (рис.5). Только контраст интерференционных полос будет возрастать не к точке ω=0, а к точкам ω± ω₀ . Вблизи точки ω=0 контраст будет минимальным.

 

 

 

 

 

 

 

 

 

 

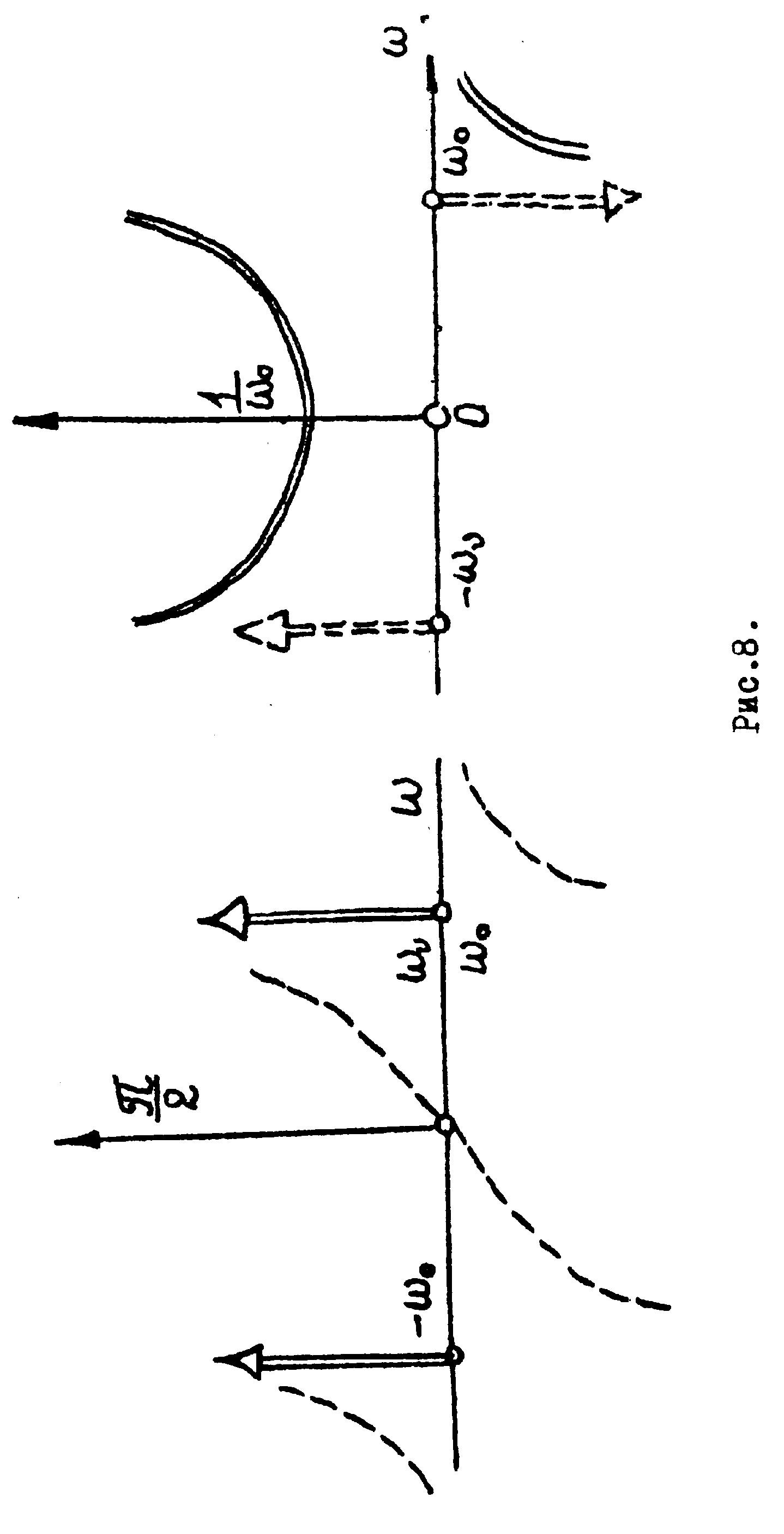
В случае несимметрии в расположении синусоидальной решётки средняя засветка, ω=0, уменьшается до величины 1/ω. Фактически это идеализированная картина, которая в реальном эксперименте осложняется явлением дифракции на конечной апертуре. В случае синусоиды это приведёт к выбросам вокруг точки ω=0. Конечность апертуры также уничтожает сингулярности вида .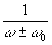

Пример. Косинусоида конечной длины

 

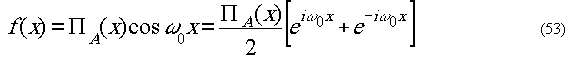
Фурье-образ такой функции равен

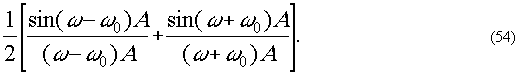
Свертка и линейный фильтр. Если на вход линейного фильтра подан единичный дельта-образный сигнал, то на выходе фильтра появится отклик фильтра на единичный сигнал, то есть функция, являющаяся кривой разрешения g(x). Эта функция полностью характеризует процесс прохождения через линейный фильтр произвольного сигнала f(x). Действительно, для этого сигнал f(x) разбиваем на совокупность достаточно малых участков, каждый из которых аппроксимируется соответствующим образом нормированной дельта-функцией, и находим сумму элементарных откликов на выходе. Каждый элементарный отклик равен отклику фильтра на единичный сигнал, сменённому в точку ξ. Учитывая нормировку и производя интегрирование по всем ξ мы получим результирующий сигнал на выходе фильтра. Замена аргумента х на х-ξ является результатом сдвига функции g(x) в точку ξ. Окончательно получим

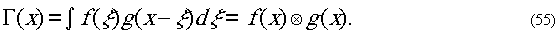
Интегральная операция (55) над двумя функциями f(x) и g(x) называется сверткой.

Основная теорема свертки. Фурье-образ свертки двух функций f(x) и g(х) равен произведению Фурье-образов f(ω) θ g(ω) исходных функций:

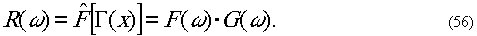
Если измерить r(ω) и заранее знать g(ω), то можно найти f(ω), а затем и сам исходный сигнал f(x):

Вопрос о том, в какой степени зашифрованную линейным фильтром ин-формацию можно расшифровать и найти искомый сигнал, здесь подробно не рассматривается. Важным фактором здесь являются шумы, задающие соотношение между шириной функции g(x) и предельным пространственным разрешением, с которым можно восстановить функцию f(x). Сделаем здесь лииь самые общие замечания.

Разрешающая способность. Последнее исследование в области теории информации показывает, что ответ на вопрос, что такое разрешающая способность, в общем случае сформулировать невозможно.Также невозможно проанализировать общий случай. Очень многое зависит от условий наблюдения, влияния априорной информации, а также исходных пожеланий экспериментатора. Поэтому проблему разрешения приходится ставить и решать каждый раз по-разному. Наиболее старой и наиболее разработанной проблемой является задача разрешения двух тесных компонент дублета, имеющих примерно одинаковую интенсивность. Давно существует критерий Рэлея, который отождествляет разрешающую способность спектрометра обнаружить дублет с его приборной шириной.

Однако фактическая разрешающая способность спектрометра может быть существенно меньше ширины кривой разрешения. Реализовать эту возможность, эквивалентную так называемому "сверхразрешению", можно с помощью изложенных выше соотношений.

Пусть нам задана кривая спектрального разрешения g(x). Чем лучше мы её знаем, тем надёжнее мы сможем выполнить операцию восстановления. Ошибка в g(x) перенесётся на ошибку f(x), а это приведёт к размытию кривой f(x) и, следовательно, к уменьшению разрешающей способности. Неточности в измерении g(x) можно считать шумами, и поэтому возникает естественный вопрос: как сказы-

ваются шумы на величину разрешающей способности.

Рассмотрим Фурье-образ g(ω) кривой разрешения g(x) (рис.9) для некоторого типичного случая. Обычно g(ω) - монотонно спадающая функция ω. Начиная с некоторого значения ω, появляются шумы. Точно установить эту границу между двумя областями кривой g(ω) очень трудно. Но,как правило, можно установить на кривой g(ω) положение излома при ω_max. Слева от этого излома находится информационная область, а справа - безинформационная область, где преобладают щумы и установить истинное поведение Фурье-образа кривой разрешения здесь невозможно.

 

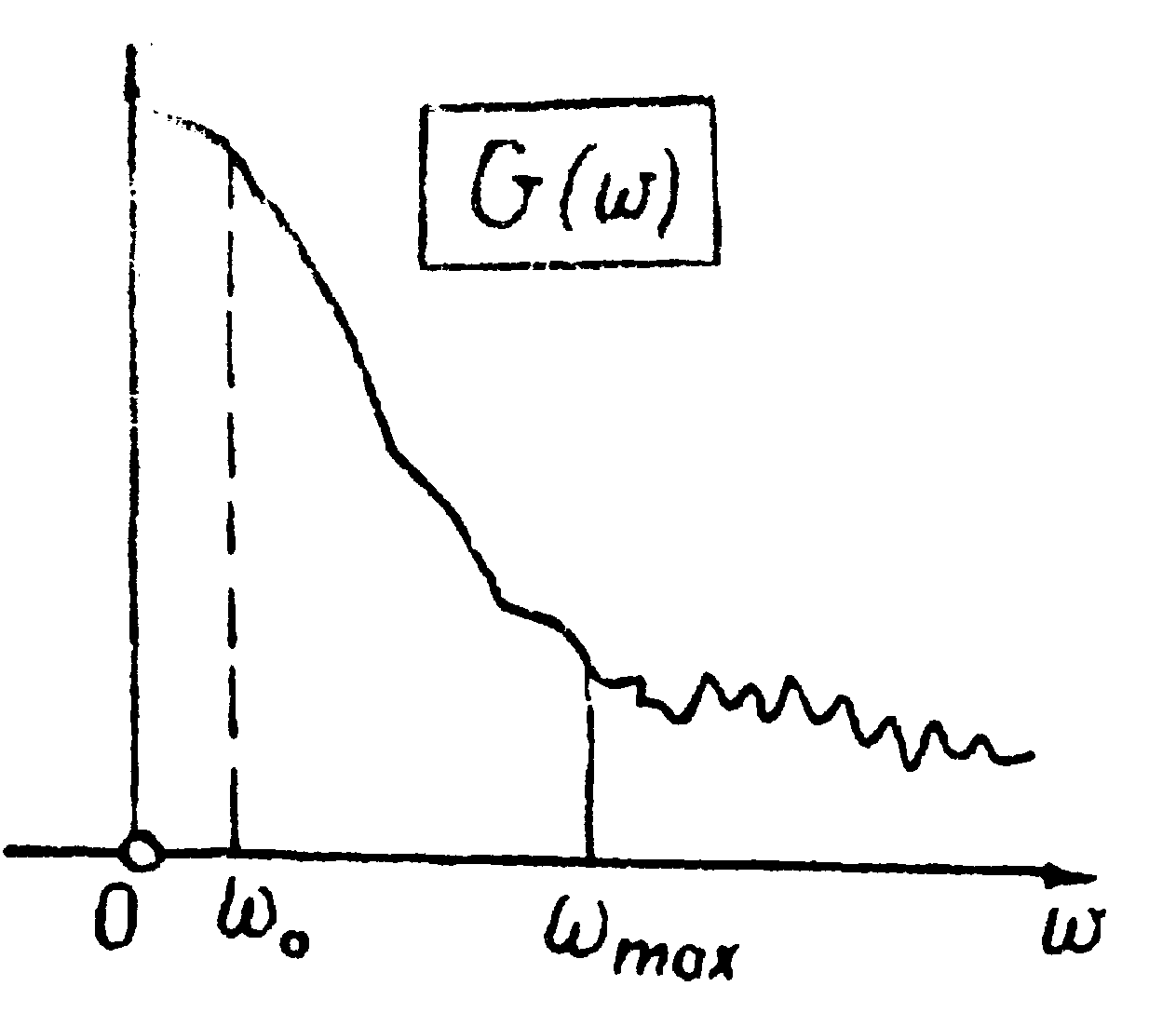
Рис.9.

 

 

Обычно кривую разрешения g(x) характеризуют одним параметром Δ - полушириной на полувысоте. Этому параметру соответствует некоторая частота ω₀, причём

Поскольку кривую разрешения мы можем провести по измеренным точкам с гораздо большей детачями, чем величина Δ , то это приводит к тому, что называют сверхразрешением. Бесконечно мелкие детали кривой g(x) невозможно установить из-за зернистости, конеч-

ного времени наблюдения и из-за многих других факторов. Это приводит к пределу, который характеризуется максимальной пространственной частотой ω_max. Область частот ω>ω_max полезной информации о кривой g(х) фактически не содержит. Коэффициентом сверхразрешения назовём отношение

При этом ω₀ связано с критерием Рэлея, определяющим условия визуального расщепления компонент дублета. Величина ω_max даёт условие информационного расщепления тесных компонент. Для нахождения величины ω_max требуется сначала найти Фурье-образ кривой g(x).

Аналогичные соотношения имеют место в гамма-спектроскопии, в оптической спектроскопии и, конечно, в голографии и в оптических системах обработки информации.

Дублет в функции f(x) проявляется на кривой r(ω) или f (ω) в виде минимума. Чем меньше эффект шумов, тем больше пространственная частота, при которой ещё можно заметить минимум. Здесь имеется прямая аналогия с опытам А.Майкельсона, которому удалось определить угловые размеры звёзд, истинных изображений которых ещё никто не видел. В звёздном интерферометре были извлечены очень высокие пространственные частоты по наблюдению контраста интерференционных полос.По положению минимума кривой видимости полос были найдены угловые размеры звёздных дисков.

Итак, мы видим, что информационная разрешающая способность оптической системы зависит от уровня шумов, содержащихся в кривой g(x). Она может быть существенно лучше визуальной разрешающей способности, определяемой шириной кривой g(x).

Все вышесказанное относится к случаю дублетной структуры объекта. Для мультиплетов или более сложных входных сигналов полученные выводы применять непосредственно нельзя.

Однако существует такой класс функций g(x), с помощью которых можно решить задачу расшифровки для входных сигналов произвольно сложного вида.

Функция g(x) играет роль колирующего элемента. Поэтому её можно использовать и качестве модулирующего носителя. Это исполь-

зуется в системах шумоподобной модуляции. Единичный дельта-образный сигнал даёт на выходе системы шумоподобный сигнал g(x). Функция g(x) должна удовлетворять двум условиям:

1) чтобы величина ω_max кривой g(х) была не ниже тех частот, которые содержатся в полезном сигнале; для этого функция g(ω) не должна быстро спадать и должна иметь как можно более плоскую часть; иначе говоря, функция g(x) должна быть близка к белому шуму;

2) для того, чтобы осуществить обратное преобразование, в частности, в голографических системах, необходимо, чтобы

т.е. автосвертка модулирующего носителя должна быть очень узким сигналом и интенсивность боковых лепестков автосвертки определяла бы информационное разрешение системы. Схема работы системы с использованием шуыоподобной модуляции приведена на рис.10.

Преобразование Френеля. Процесс дифракции света можно рассматривать как линейную фильтрацию. Роль функции g(x) выполняет функция Френеля

где

λ - δлина волны света, q - расстояние от транспаранта. Функция Френеля удовлетворяет условию, аналогичному условию (61),а именно:

Преобразованием Френеля называется свертка вида

Это преобразование является обратимым:

 

---

---

 

 

 

 

 

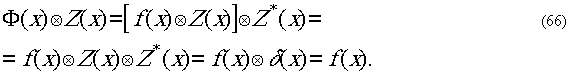
Рис.10.

Фурье-образ функции Френеля равен

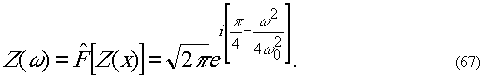
Имеет место следующее тождество

 

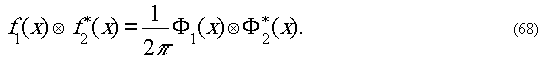
Кроме этого,

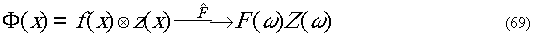
или в явном виде через Фурье-образ

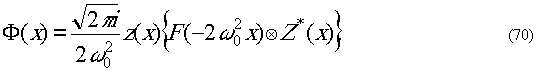
Соотношения (60) - (70) даны для одномерного случая.

Преобразования Фурье и преобразования Френеля описывают два наиболее важных случая дифракции света: дифракцию Фраунгольвера или дифракцию далёкого поля и дифракцию Френеля.

Преобразование Френеля эквивалентно следующей последовательности операций над Фурье-образом исходного сигнала (70):

1) свертка Фурье-образа с комплексно-сопряжённой функцией Френеля;

2) умножение на функцию Френеля.

Возможна также другая последовательность операций:

1) свертка Фурье-образа с Фурье-образом функции Френеля;

2) умножение на Фурье-образ комплексно-сопряжённой функции Френеля (71)

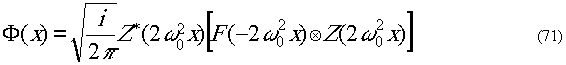
Френелевский образ исходной функции, умноженный на компенси-рующий множитель сходящейся сферической волны, оказывается равным свертке Фурье-образа исходной функции с заменой x на -x со сходящейся сферической волной.

Умножение Френелевского образа исходной функции на сферическую волну равно свёртке Фурье-образа исходной функции со сферической

волной

Также имеет место следующее обратное соотношение

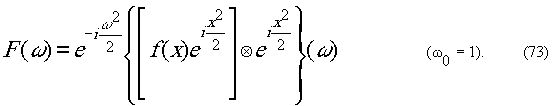
На использовании этих соотношений построен сандвич Френеля, описанный в книге Л.Мерца.

Визуализация фазового контраста λ/4 фазовой пластинкой. Поместим транспарант, пропускание которого является чисто фазовым

t(x)=e^iΦ(x) (74)

в систему оптического преобразования Фурье. Пусть фазовые вариации малы, так что

t(x)≈1+iΦ(х). (75)

В плоскости Фурье имеем

Составляющая δ(x), пройдя через фазовую пластинку толщиной λ/4, превратится в сигнал

На выходе фильтра имеем

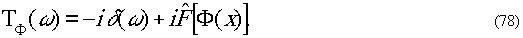
При обратном преобразовании Фурье получим преобразованный сигнал

t_{преобр.}(x)=-i+iΦ(x)=-i[1-Φ(x)]. (79)

Детектор света воспримет распределение интенсивности

i_{преобр.}(x) = |t_{преобр.} (x)|² = |1-Φ(x)|² ≈ 1-2Φ(x). (80)

Отфильтрованное изображение имеет контраст интенсивности, пропорциональный фазовому контрасту. Ещё больший контраст получается, если, кроме фазового сдвига на Δφ=π/2, ослабить нулевую частоту также по интенсивности в α² раз. Тогда

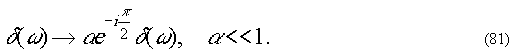
Отфильтрованный спектр имеет

 

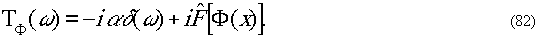
Отфильтрованное изображение имеет амплитуду

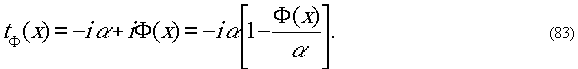
Контраст интенсивности в 1/α раз больше фазового контраста.

Нож Фуко. Преобразовать фазовый контраст в контраст интенсивности можно с помощью ножа Фуко, который срезает половину пространственных частот. Пусть исходный сигнал имеет вид

t(x)≈1+iΦ(x). (84)

Фурье-образ функции Φ (х) равен

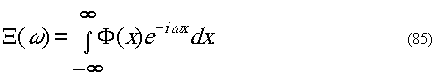
Обратное преобразование в отсутствие ножа Фуко запишется в виде

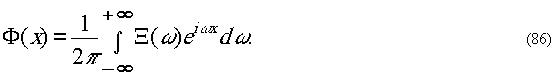
Нож Фуко, установленный в плоскости Фурье, срезает частоты -∞<ω<0. акая операция эквивалентна умножению Фурье-образа Ξ(ω) на функцию Хэвисайда y(ω). При обратном преобразовании Фурье возникает искажённый сигнал

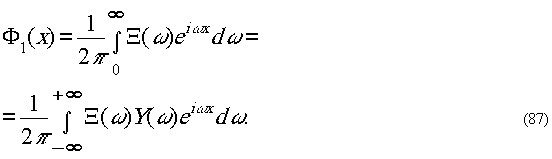
Воспользовавшись теоремой свертки, находим

Φ₁(x)=Φ(x)⊗u(x), (88)

где

Окончательно находим

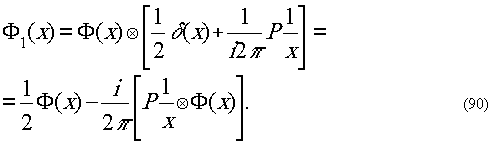
Пренебрегая квадратичными членами по Ф(х), находим амплитуду мскавённого изображеня

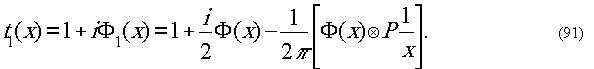
Распределение интенсивности равно

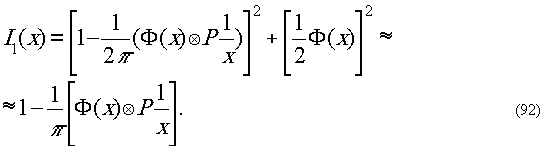
Преобразование Гильберта. С помощью преобразования Гильберта удаётся подвергнуть единой операции как дифракционный пик Фурье-образа, расположенный около нулевой прострсанственной частоты,так и сам сигнал. Этим удаётся устранить низкочастотные выбросы, возникающие в методе λ/4 пластинки, а также перекосы и сдвиги изображения, вызываемые ножом Фуко. Кромe этого, при преобразовании Гильберта используется весь свет, и яркость и контраст оказываются очень высокими. Подвергнем исходную функцию f(x) преобразованию Гильберта. Получим функцию χ(x), которая равна

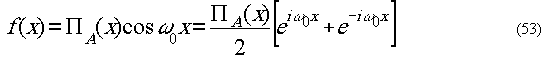
Интегрирование ведётся в смысле главного значения. Поскольку функция 1/πч, являющаяся сомножителем операции свертки, при преобразовании Фурье превращается в функцию i sgnω , то преобразование Гильберта в плоскости х эквивалентно операции фильтрации в плоскости Фурье с помощью фитьтра, амплитудное пропускание которого равно

i, ω>0

g(ω) = i sgnω = (94)

-i, ω<0.

Из (94) видно, что преобразование Гильберта осуществляется с помощью транспаранта, имеющего чередующиеся фазовые сдвиги Δ=± π/2 в квадрантах, согласно рис.8.

Метод визуализации фазового контраста с помощью преобразования Гильберта характеризуется тем, что полная интенсивность исходного и преобразованного изображения одинакова. Это вытекает из соотношения

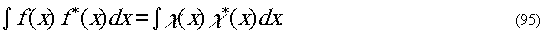
Метод преобразования Гильберта пригоден как к большим, так и к малым сдвигам фаз в фазово-контраством изображении.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Таблица

Сводная таблица сверхточных преобразований

Преобразования	Ядро	Вид Фурье-фильтра
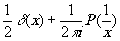
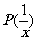
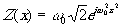
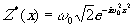
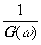
Свертка и шумоподобная модуляция. Деконволюция и демодуляция при шумоподобной модуляции. Нож Фуко.   Преобразование Гильберта. Преобразование Френеля. Обратное преобразование Френеля.	g(x)	g(x)         y(ω) eiπ/2, ω>0 i sgnω= e-iπ/2, ω<0

 

 

 

 

 

 

 

 

 

 

 

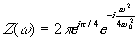
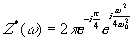
Л и т е р а т у р а

1. a.papoulis, "systems and transforms with applications in optics", new-york, mc graw-hill, 1968.

2. j.arsac, "tranaformation de fourier et theorie des distributions", dunod, paris, 1961.

3. Я.И.Хургин, В.П.Яковлев. Методы теории целых функций в радиофизике, теории связи и оптике. М., 1962.

4. r.bracewell, "the jfourior transform and its applications", mc graw-hill book company, 1965.

5. l.brilouin,"scientific uncertainty and information", academic press, new-york - london 1964,

6. Л.М.Сороко. Фурье-алгоритм обработки спектральной информации в ядерной физике. Сообщение ОИЯИ, 1-5030, 1970.

7. Дж.Строук. Введение в когерентную оптику и голографию.

Мир, 1967.

8. s.lowenthal, y.belvaux, "observation of phase objects.by

optically processed hilbert transform", appl. phis.lett.,