|
|
 |
 |

|
| |
МЕТОДЫ ИЗМЕРЕНИЯ КОГЕРЕНТНОСТИ ИЗЛУЧЕНИЯ ЛАЗЕР ob Е.П.Остапченко, В.А.Степанов
Вoпpocy измерения когерентности в настоящее время посвящено большое количество работ. В данной лекции кротко характеризуются известные подходы к измерению когерентности и дается описание некоторых экспериментальных установок.
Вез известные методы, по-видимому, можно свести к следующим четырём:
1) интерференционные,
2) дифракционные,
3) голографические,
4) поляризационные.
Последовательность их расположения выбрана произвольно, более того, каждый из этих подходов не является независимым. Так, например, голографический метод измерения когерентности подразумевает интерференцию двух пучков, один из которых несёт информацию о предмете, а второй является опорным, а поляризационный метод -интерференцию пучков, разность хода между которыми изменяется с помощью поляризационных призм. Тем не менее, такое разделение имеет смысл, так как каждый из подходов характеризуется только ему присущими чертами. Кроме того, данное разделение отображает тот факт, что исторически все вышеприведённые методы появились неодновременно.
Наиболее устоявнимиоя являются интерференционные измерении степени когерентности, когда |γ (p1,p2,τ)| определяется как
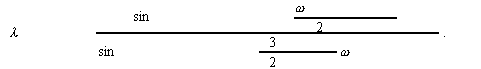
где v=(iмакс-iмин)/(iмакс+iмин) - видимость интерференционной картины, получаемой в результате интерференции двух волн, исходящих из точек Р1 и Р2; τ - время запаздывания одной волны относительно другой; i1 и i2 - интенсивности этих волн; iмакс - интенсивность
светлой полосы интерференционной картины, а iмин - интенсивность соседних с ней тёмных полос. Простейшими интерферометрами, в которых реализуется интерференция двух волн, являются интерферометр Юнга с двумя отверстиями или целями и интерферометр Майкельсона.
Интерферометр Юнга используется для измерения пространственной когерентности излучения /1/. Схема экспериментальной установки приведена на рис.1. Лазерный пучок света, предварительно уширенный с помощью системы двух линз λ1 и λ2, попадает на непрозрачный экран с двумя отверстиями, расстояние между которыми может изменяться произвольньм образом. Интерференционная картина, получаемая в результате интерференции волн, выходящих из отверстия, наблюдается в фокальной плоскости линзы λ3. Определение пространственной когерентности γ(p1,p2,0) в пучке сводятся к измерению видности интерференционных полос (iмакс. и iмин.) при различных расстояниях между Р1 и Р2. Это измерение можно осуществить как фотоэлектрическим методом, когда фотоприемником сканируется интерференционная картина и регистрируется фототек, пропорциональный интенсивности света, так и фотографическим методом, когда интерференционная картина фотографируется и в дальнейшем фотометрируется. Информацию о когерентных свойствах лазерного пучка несут функциональные зависимости γ(d) , где d- расстояние между Р1 и Р2 в пучке.
С помощью интерферометра Майкельсона /2/ обычно измеряют временную когерентность излучения лазера γ(τ) (πис.2а). При этом
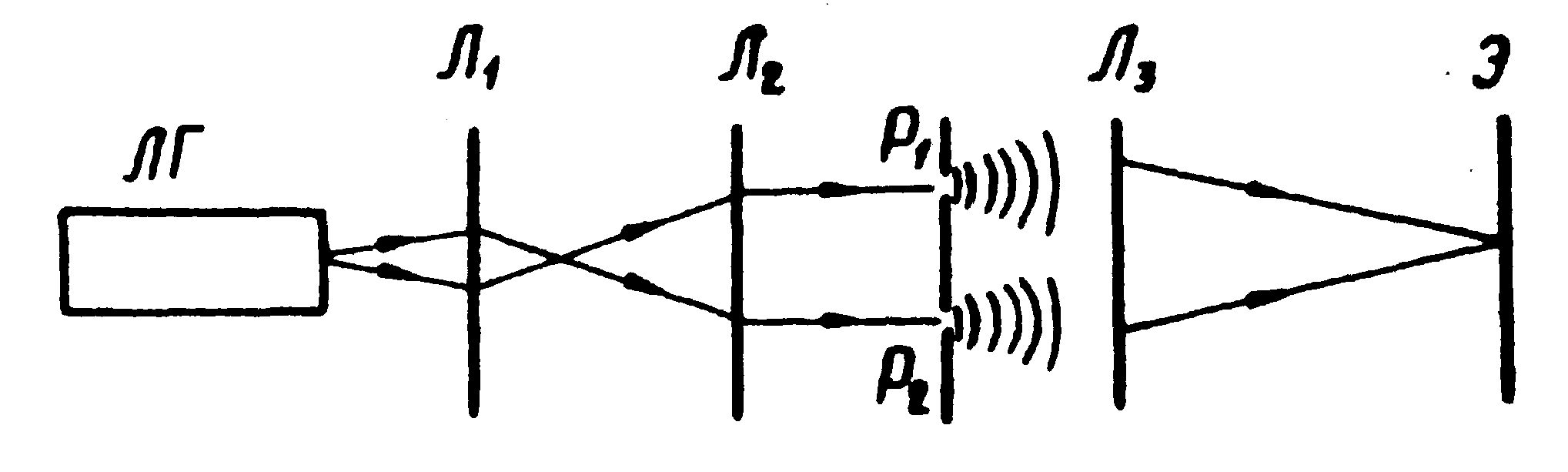
Рис.1. Интерферометр Юнга.
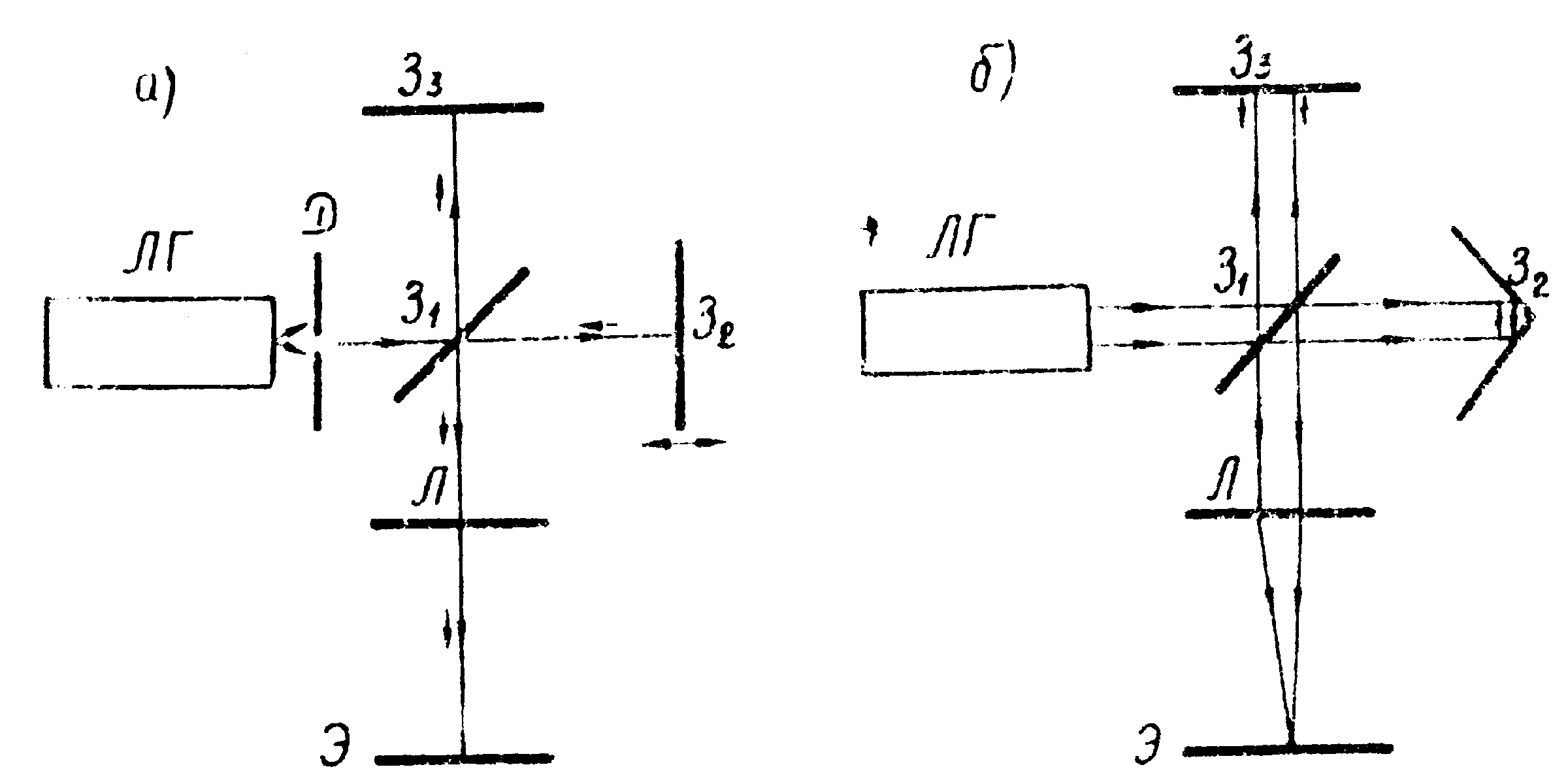
Рис.2. Интерферометр Майкельсона:
а) для измерения временной когерентности излучения ОКГ;
б) для измерения пространственной когерентности излучения ОКГ;
после лазера ставится диафрагма, огранчивающая лазерный пучок. Интерференционная картина, получаемая вследствие интерференции между двумя частями луча, задержанными относительно друг друга на время τ, пропорциональное разности длин плеч интерферометра, наблюдается в фокальной плоскости линзы λ. Определение γ (τ) ρводится и измерению видности интерференционной картины при различных τ. Информацию о временной когерентности луча несёт функциональная зависимость γ(τ) θли время задержки τк, называемое временем когерентности, при котором | γ(τ)≥0,91|. Разность хода Δlk=cτк, где с- скорость света, есть длина когерентности.
На рис.2б представлена схема видоизменённого интерферометра Майкельсона /3/, предназначенного для измерения пространственной когерентности. В интерферометре отсутствует диафрагма d, ограничивающая пучок, и вместо подвижного зеркала З2 используется уголковый отражатель, сдвигающий фазы всех точек пучка на π. При этом в фокальной плоскости линзы λ наблюдается интерференция пучка ла-
зера со своим зеркальным отображением. Такой интерферометр может заменить интерферометр Юнга, в котором отверстия (щели) раздвигаются симметрично относительно центра пучка. Для определения функции пространственной когерентности γ(p1,p 2,0) с помощью данного интерферометра вполне достаточно одной интерференционной картины; процесс обработки экспериментальных результатов влючает в себя вычисление видности интерференционных полос v(x) для каждого максимума и минимума от центра к краю пучка (х - расстояние, отсчитываемое от центрального максимума интерференционной картины, равное d/2). Функциональная зависимость γ(d) , полученная с таким интерферометром, не даёт полной информации о пространственной когерентности лазерного излучения, однако во многих практических случаях её бывает вполне достаточно.
В /4/ для измерения функции пространственной когерентности предложена схема, представленная на рис.3. В данной схеме интерферируют лучи, выведшие с противоположных сторон лазера и проведшие одинаковые пути, что эквивалентно в случае симметричного резонатора лазера интерференции пучка со своим зеркальным отображением, так как фазы лучей, вышедших с противоположных сторон
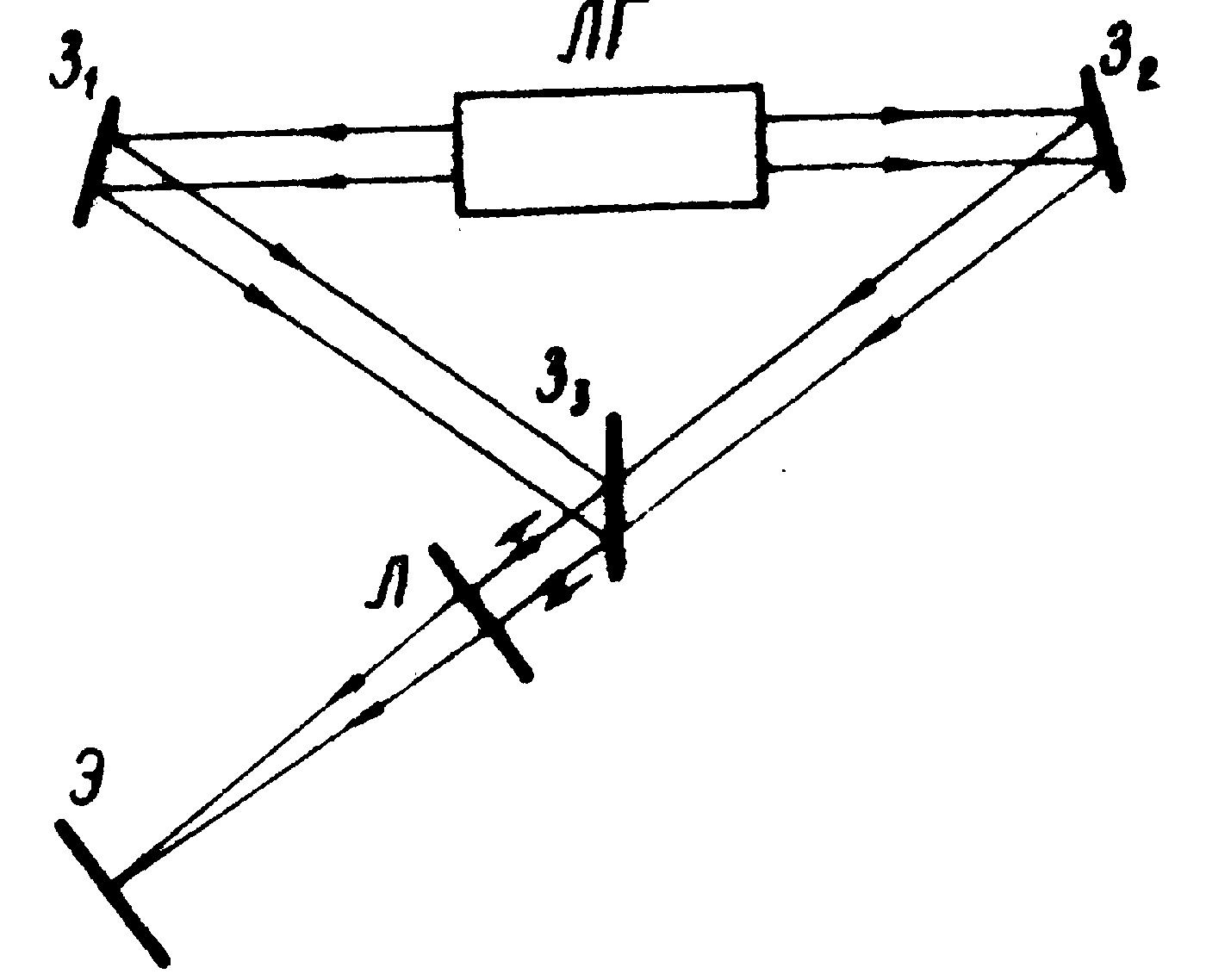
Рис.3. Схема интерференции двух пучков, выходящих с противоположных сторон ОКГ.
лазера отличаются на π. В этом случае анализ полученной интерференционной картины аналогичен предыдущему.
Необходимо заметить, что измерение когерентности с помощью интерферометров не ограничивается использованием вышеуказанных схем. Схемы, представленные выше, являются, по-видимому, наиболее простыми .
Дифракционный подход к измерению когерентности пока не получил столь широкого распространения, как интерференционный, но, несмотря на это, является очень важным, так как показывает, что информацию о пространственной когерентности не обязательно получать с помощью сложных вспомогательных схем, служащих для образования двух волн или двух пучков. Её можно извлечь из картины распределения интенсивности в дифракционном поле /5,6/, образованной зa счёт дифракции волны на апертуре произвольной конфигурации, причём в качестве апертуры, в принципе, может служить и выходное зеркало лазера. Иными словами, дифракционный подход подчеркивает, что когерентность, как свойство излучения, заложена в самом пучке и не зависит от схем измерения.
Вычисление интенсивности в дифракционном поле производится по формуле:
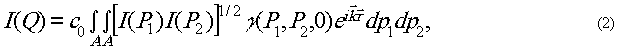
где i(p1) i(Р2)-
интенсивности на произвольных бесконечно малых площадках
dp1, dp2 с
центрами в точках Р1
и Р2;
γ(Π1, Р2,0 )-комплексная
степень пространственной когерентности между волнами, исходящими из точек Р1
и Р2; 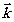 - волновое число;
- волновое число; 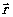 -расстояние от апертуры до плоскости наблюдения; с0
- постоянная, зависящая от размеров апертуры; А - площадь апертуры.
-расстояние от апертуры до плоскости наблюдения; с0
- постоянная, зависящая от размеров апертуры; А - площадь апертуры.
Задача определения комплексной степени пространственной когерентности математически сводится к решению интегрального уравнения (2). Для излучения лазера эта задача решена в работах /5,6/, в которых показано, что

где i (q)- интенсивность в дифракционной поле, iа(Р)- интенсивность на апертуре.
Из выражения (3) видно, что определение комплексной степени пространственной когерентности экспериментально производится с помощью измерения интенсивностей в дифракционном поле и на апертуре.
Сравнительно новыми методами измерения когерентности являются голографические и поляризационные методы. Рассмотрим голографический подход. В работе /7/ показано, что модуль комплексной степени пространственно-временной когерентности лазерного пучка прямо пропорционален интенсивности восстановленного из голограммы изображения и обратно пропорционален освещенности объекта во время экспонирования, т.е.

где Р 0- точка падения луча на голограмму при восстановлении, а Р - произвольная точка пучка; τ - время запаздывания волн, исходящих из точек Р1 и p2. Из (4) видно, что для определения функции когерентности |γ(p0,p i,τ)| экспериментально достаточно измерить освещённость объекта и интенсиdность восстановленного изображения.
На рис.4 представлена схема получения Фурье-голограммы диффузно рассеивающего объекта /8/, которая используется для определения функции пространственной когерентности.
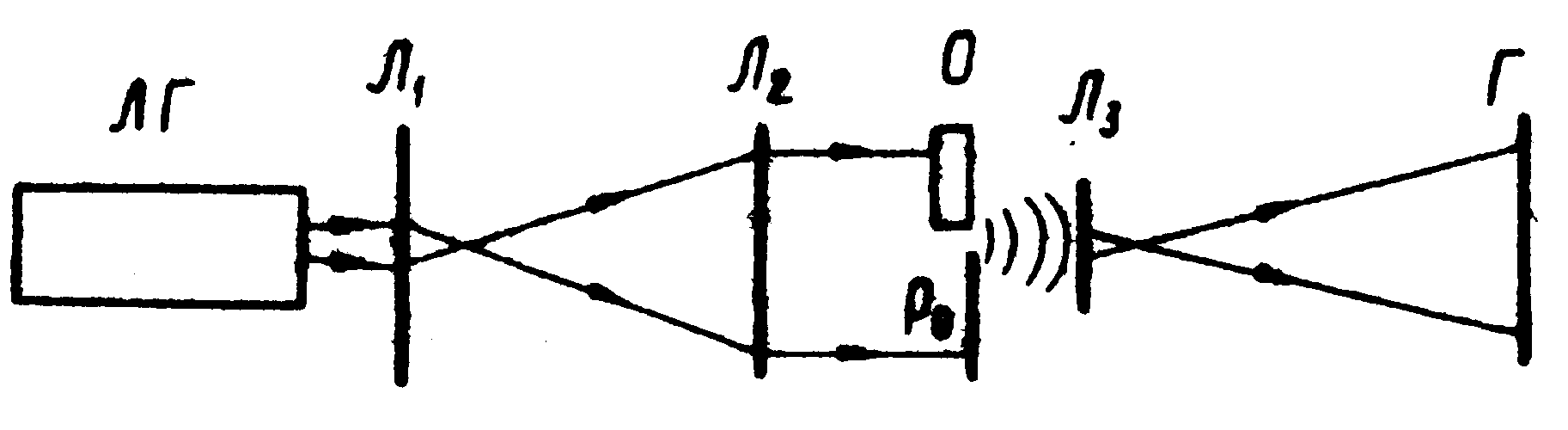
Рис.4. Схема Фурье-голографирования в частично когерентном свете.
Как видно из рисунка 4, пучок лазера уширяется с помощью системы двух линз и попадает на диффузии рассеивающий объект. Часть света ограничивается диафрагмой и используется в дальнейшем в качестве опорного пучка при голографировании и восстановлении изображения. При восстановлении изображения объект накрывается, а перед полученной голограммой ставится собирающая линза. Восстановленное изображение наблюдается за плоскостъю голограммы. Измерение интенсивности производится с помощью фотографирования и дальнейшего фотометрирования. Эта голографическая схема позволяет определить модуль пространственной когерентности между точками Р0(отверстие диафрагмы d) и всеми другими точками пучка. Аналогичную задачу можно решить и с помощью схем голографирования Френеля-Фраунгофера /9/ Данная задача определения |γ(p0,p i,τ)| несколько упрощена, поскольку в результате находится лишь Функция корреляции между одной точкой Р0 и многими точками пучка pi.
Для определения функций корреляции между произвольными точками лазерного пучка, как показано в /l0/, необходимо в качестве опорного пучка использовать весь пучок, а не его часть. Меняя положение точки падения опорного луча Р0 при восстановлении, можно определить степень корреляции между любой точкой в пучке и остальными, т.е. семейство функций когерентности.
На рис.5 представлена схема для определения семейства таких функций когерентности.
Луч лазера, расщепляясь предварительно на два пучка с помощью разделительного зеркала З 1, фокусируется на диффузно рассеивающем объекте и используется одновременно в качестве опорного. Плоскость Г- плоскость голограммы данного диффузного объекта. При восстановлении изображения объект закрывается, а на пути опорного луча ставится линза, фокусирующая луч в точку Р0 голограммы. Восстановленное изображение фотографируется за плоскостью голограммы. Меняя положение точки Р0 , можно определить степень когерентности между любыми точками лазерного пучка.
Голографические методи могут быть испильзованы и для измерения модуля функции временной когерентности |γ(τ)|. cxeμа
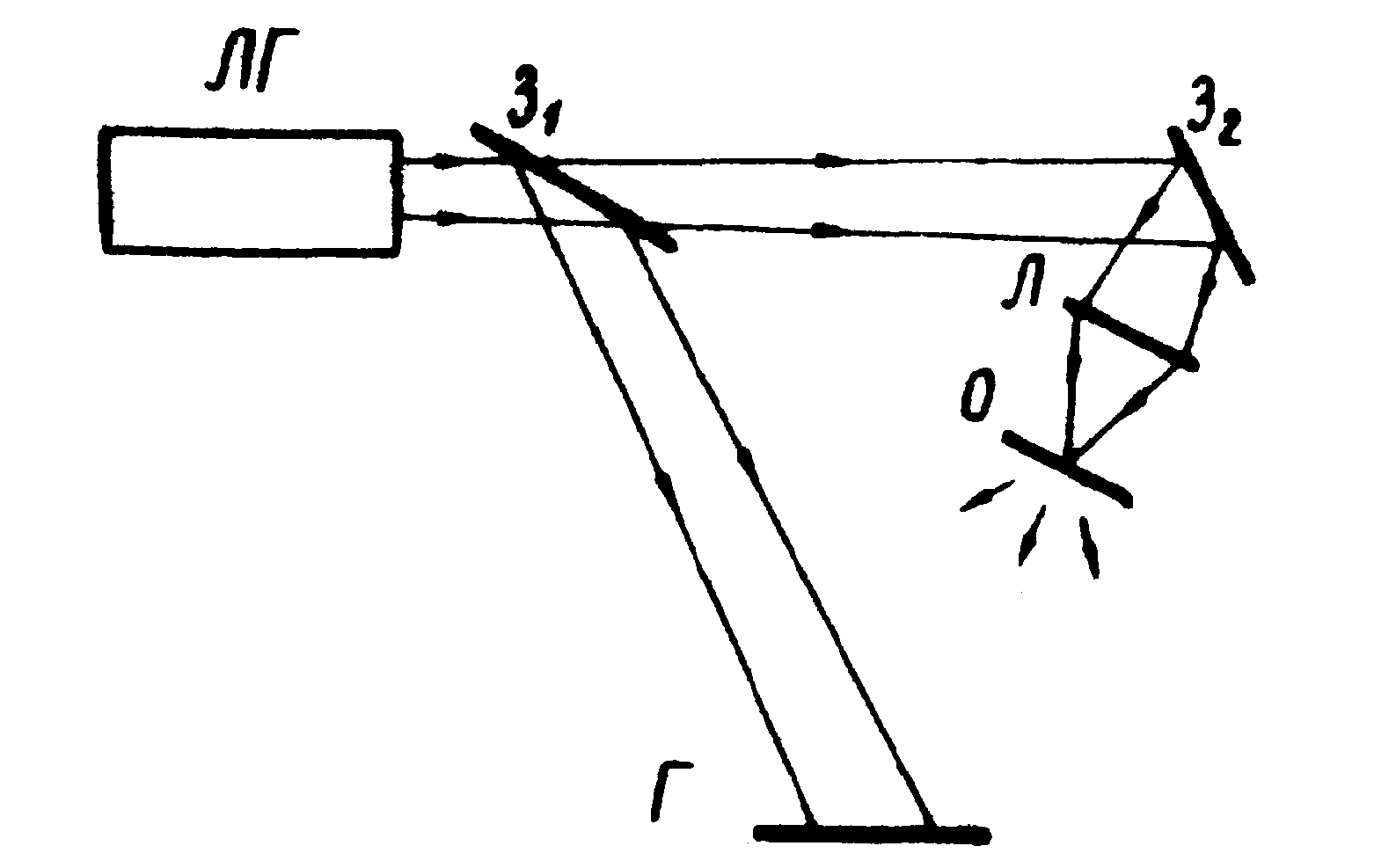
Рис.5. Схема голографического измерения пространственной когерентности излучения ОКГ.
для измерения временной когерентности лазерного излучения пред ставлена на рис.6.
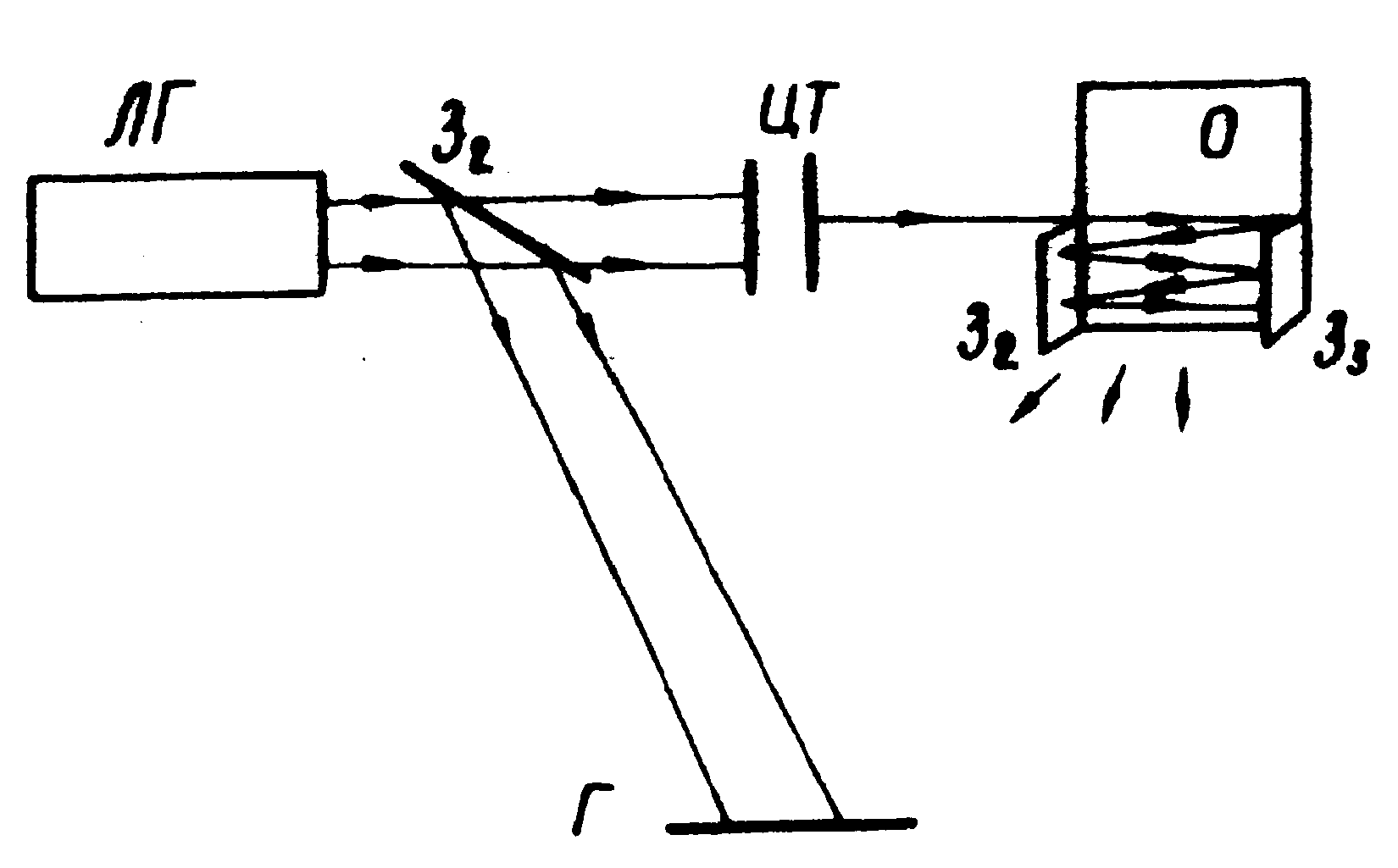
Рис.6. Схема голографического измерения временной когерентности излучения ОКГ.
Как показано на рис.6, луч лазера с помощью разделительной пластинки З 1 расщепляется на две части, одна из которых расширяется в горизонтальном сечении цилиндрическим телескопом ЦТ и направляется на диффузный экран θ под небольшим углом (~1°). Последовательно отражаясь от зеркал З2 и З3, расположенных параллельно друг другу, луч лазера прочерчивает на экране светящуюся траекторию. Цуги волн, приходящие к голограмме от различных точек экрана, задерживаются относительно опорного пучка на временные интервалы, равные времени пробега сигнального пучка вдоль экрана. Поэтому восстановленное изображение, полученное при перекрытии объекта, представляет собой светящийся след лазерного луча различной яркости, что, как видно из соотношения (4), несёт информацию о временной когерентности луча. Длина когерентности при этом определяется как расстояние между соседними максимумами восстановленного следа.
Поляризационный подход к измерению когерентности, изложенный в /11/, заключается в анализе интерференционной картины, полученной в результате интерференции обыкновенного и необыкновенного луча, образованных поляризационными призмами.
На рис.7 представлена схема измерения модуля функции когерентности |γ(p0,p i,τ)| при использовании в качестве призмы поляризационной призмы Волластона. Как известно, призма Волластона состоит из двух клиньев, оптические оси которых перпендикулярны друг другу и параллельны боковым граням. Она расцепляет луч на два (обыкновенный и необыкновенный) луча, вышедшие под углом друг к другу, поляризованные в перпендикулярных плоскостях. Равность хода между этими лучами:
Δ =2(ne-n0)xtgθ, (5)
где n0 и ne - показатели преломления для обыкновенного и необыкновенного лучей, θ - угол при вершине призмы. На пути лучей ставятся поляризационный светофильтр и линза. Интерференция в плоскости экрана происходит только между лучами, пришедшими и одно и то же время. Поэтому введение разности хода Δ позволяет получить интерференцию пучка как бы с несколько сдвинутой его
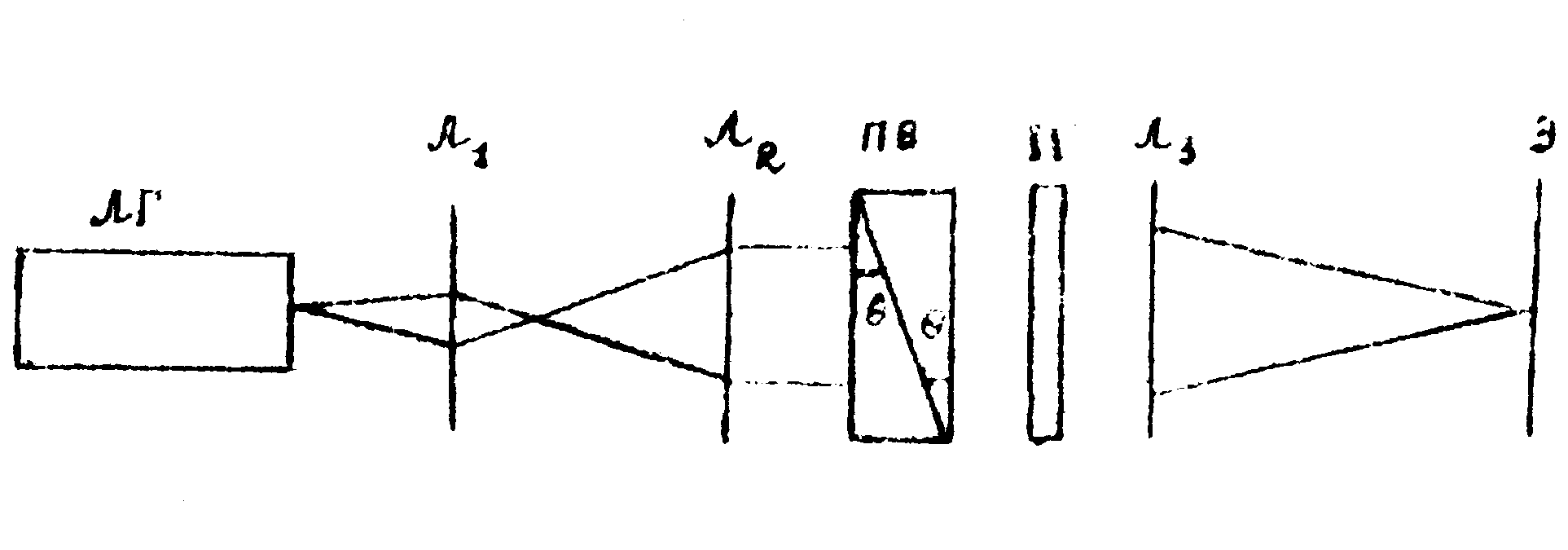
Рис.7. Поляризационный интерферометр.
копией. При разности фаз δ =2πΔ/λ=π θмеем интерференцию пучка со своим зеркальным отображением, как в интерферометре, изображённом на рис.2б.
Информацию о когерентности лазерного пучка могли подучить, измеряя видность интерференционных полос от центра к краю пучка. Для обычных поляризационных призм из кварца разность ne-n0≈0,01 и разность хода Δ настолько мала (Δ<<lк), что данная методика может быть использована только для измерения модуля функции пространственной когерентности |γ(p0,p i,τ)|. Очевидно, изменяя точку Р0 падения луча на призму, т.е. х, отсчитываемое сверху вниз, можно получить семейство функций пространственной когерентности, когда точки в пучке располагаются произвольным образом.
Вместе с тем, используя призмы, например, из nano3 с размерами ~10 см, в принципе, можно оценивать и временную когерентность излучения ОКГ, генерирующего несколько частот одновременно.
Кроме призмы Волластона в поляризационном методе измерения когерентности можно с успехом использовать и другую призму, например, призму Саваара.
Итак, из всего вышесказанного следует, что измерение когерентности производится с помощью самых разнообразных методик и схем, причём приведенные выше не исчерпывают их разнообразия.
Л и т е р а т у р а
1. Д.В.Гордеев, Г.В.Мелехин, А.Ф.Степанов, В.А.Степанов.
Сб. Электронная техника, серия ГРП, №4, 1968.
2. h.p.barber. josa, 57, 4, 574 (1967).
3. Р.Р.Герке, Ю.Н.Денисюк, В.И.Локшин. Оптико-механическая промышленность. №7, 22-26, 1968.
4. С.М.Наумов, И.В.Потапов. Информ. справ.листок, №02 009, 1964.
5. j.v.cornacchio, b.p.soni. nuovo cimento, 38, 3, 1169
(1965).
6. j.v.cornacchio, k.a.farnham. nuovo gimento, 42, 1, 108
(1966).
7. Е.Н.Денисюк, А.Г.Смирнов, Д.И.Стаселько. Оптика и спектрсскопия, №3, вып.26, 1969.
8. m.lurie. josa, 58, 5, 614 (968).
9. m.lurie. josa, 56, 10, 1369 (1966).
10. Е.Н.Денисюк, А.Г.Смирнов, Д.И.Стаселько. Материал семинара "Голография в контроле качества и технологических процессах", М., 1969.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

