МЕТОДЫ ПОВЫШЕНИЯ ЧУВСТВИТЕЛЬНОСТИ

ГОЛОГРАФИЧЕСКОЙ ИНТЕРФЕРОМЕТРИИ

К.С.Мустафин

Интерференционный анализ с повышенной чувствительностью привлекает к себе внимание специалистов, заинтересованных в точном контроле оптических поверхностей, в решении ряда аэродинамических и метрологических задач. Развитие голографии со своей стороны создало благоприятные условия дяя разработки оригинальных способов интерференционного анализа. В связи с этим представляет интерес разработка методов повышения чувствительности интерференционного анализа, используя специфику голографического процесса.

1. Трёхлучевая интерферометрия

Сущность рассматриваемого способа состоит в получении интерференционной картины, которая представляет собой результат взаимодействия исследуемого волнового фронта с двумя волновыми фронтами сравнения. Направление распространения этих фронтов волн выбирается так, чтобы они лежали в одной плоскости и, пересекаясь, образовали примерно равные углы между исследуемым пучком и каждым из пучков сравнения. Наблюдаемая при этом интерференционная картина имеет удвоенное значение фазового сдвига по отношению к действительному сдвигу, созданному исследуемым объектом. Поэтому такую интерферограмму можно считать полученной на длине волны, в два раза короче той, которая использовалась при получении интерферограммы, а сам метод - обладающим повышенной чувствительностью. Его реализация может происходить различными путями. Здесь будет рассмотрен метод тройной экспозиции, как наиболее простой и обеспечивающий компенсацию искажений, вносимых оптическими элементами схемы.

1. Рассмотрим аналитически изложенный выше метод. Пусть комплексные амплитуды сигнального (Е_s) и опорного (Е₀) пучков при первой экспозиции будут:

где k=2π/λ, α₀- угол голографирования, kf_s - распределение фаз, обусловленное исследуемым объектов,kf - распределение фаз, вносимое оптикой в объектном и опорное пучках соответственни, которые являются переменными по координатам х и y, выбранным в плоскости голограммы.

Для простоты изложения модули амплитуд считаем равными единице, а сам объект - фазовым.

Распределение интенсивности на голограмме при первой экспозиции будет:

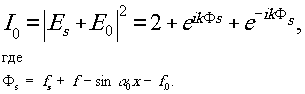
Вторая и третья экспозиции производятся при отсутствии неоднородности, вводимой объектом (f_s=0), и углах голографирования α₁ и α₂, соответственно (рис.1).

Рис.1.

Схема голографирования в методе трёхлучевой интерферометрии.

Г-голограмма: α₀- угол между опорньм О₀ и объектным пучками; α₁, α₂ - углы между пучком сравнения С и и опорными пучками О₁ и О₂ соответственно.

Аналогично предыдущему, распределения интенсивностей I₁, и I₂ на голограмме при второй и третьей экспозициях будут:

где Φ_i = f-f₀-sinα₁x (i = 1,2). (4)

При линейной записи для амплитудного пропускания можно написать

T_a = c(I₁+I₂+I₃). (5)

Согласно (5), (2) и (3), освещение голограмм в плоский вопновой (рис.2) приводит к появлению восстановленных волн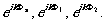

Рис.2.

Схема получения интерферограммы:

N - нормаль к голограмме Г, β₁ и β₂ - углы дифракции восстановленных волн сравнения С₁ и

С₂, соответственно.

 

Распределение интенсивности, которое наблюдается при наложении этих волн, будет соответствовать уравнению:

I=3+3[Cosk(Φ_s-Φ₁)+Cosk(Φ_s-Φ₁)+Cosk(Φ₁-Φ₂)] (6)

или

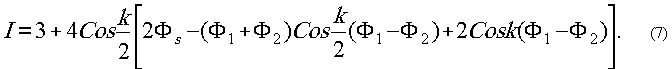
Подставляя значения Φ_s, Φ₁, Φ₂, получим

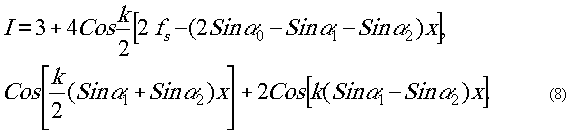
Рассмотрим второй член выражения (8). Здесь в зависимости от соотношения α₀, α₁, α₂ могут быть два случая:

|2Sinα₀-Sinα₁-Sinα₂|<|Sinα₁-Sinα₂| (9)

и

|2Sinα₀-Sinα₁-Sinα₂|>|Sinα₁-Sinα₂| (10)

Неравенство (9) выполняется в том случае, когда значение величины Sinα₀ заключено в интервале значений Sinα₁ и Sinα₂.

При этом интерференционная картина может получаться как в полосах конечной, так и бесконечной ширины любой ориентации.

Образование полос той или иной ширины следует из уравнения (8), причём значения углов должны удовлетворять неравенству (9).

Действительно, уравнение (8) показывает, что в наблюдаемой картине содержатся интерференционные полосы, определяемые членом

Период этих полос зависит от угла между опорными пучками при второй и третьей экспозициях. Сомножитель

характеризует собой интерференционные полосы конечной ширины с удвоенным значением фазового сдвига, вносимого объектом.

Период этой картины определяется разностью приращений углов

(Δα=α₀-α₁ и Δα=α₂-α₁), созданных опорными пучками при первой экспозиции. При удовлетворении неравенства (9) система полос (11) является несущей, которая модулируется членом (12) по амплитуде. Ее появление не умаляет достоинств интерференционной картины, а наоборот, она может служить хорошей метрической сеткой при расшифровке интерферограмм. Период модулирующей функции (т.е. период полос настройки) определяется уравнением:

Как следует из (12), для получения интерферограммы в полосах бесконечной ширины (Δx=: ), также с удвоенным значением фазового сдвига, необходимо выполнить условие:

Иными словами, требуется, чтобы приращения углов между опорными пучками были равны.

В случае, когда углы голографирования удовлетворяют неравенству (10), информация об объекте (f_s) по-прежнему содержится в члене (12), который теперь, однако, выступает в роли несущей, а член (11) - модулирующей функции. Очевидно, что этот случай имеет место, когда значение величины Sinα₀, находится вне интервала значений Sinα₁ и Sinα₂. В этом случае картина представляет собой обычную интерферограмму, модулированную по амплитуде с периодом

В обоих случаях за рассмотренную картину накладываются интерференционные полосы, обусловленные третьим членом выражения (5). Но этот член не меняет общую картину, и все выводы, сделанные без его учёта, остаются в силе.

Важно отметить, что в выражении (8) фазы не содержат члены f и f₀. Это означает, что фазовые возмущения, обусловленные нека-

чественной оптикой в объектной и опорном пучках, не вносит вклада в интерференционною картину.

В рассматриваемом методе могут возникнуть трудности при расшифровке, ввиду появления трёх изображений предмета, соответствующих трём экспозициям. Очевидно, что смещения двух изображений относительно центрального будут характеризоваться величинами Rtg(α₁-α₀) и R tg(α₀-α₁), где R - расстояние от объекта до голограммы. Эти затруднения можно устранить, если взять R=0, т.е. производить голографирование фокусированного изображения предмета.

Следует отметить, что в рассмотренном методе несущественно, в какой последовательности совершается экспонирование. Кроме того, получение интерферограмм может происходить любым из способов, указанным в /1/. Так, например, можно вначале произвести экспозиции пучков сравнения при углах голографирования α₁ и α₂, а затем, после обработки, освещать голограмму одновременно сигнальным и опорным пучками, образующими между собой угол α₀. Углы должны удовлетворять неравенству α₁<α₀<α₂ (16).

Тогда за программой в направлении распространения сигнального пучка можно наблюдать интерферограмму с удвоенной чувствительностью в реальном масштабе времени.

Реализация описанного выше метода происходила двумя путями. Один из них заключается в получении муаровой картины на самой голограмме^*, другой - в получении интерферограмм при восстановлении. Несмотря на отсутствие принципиальной разницы, при математическом рассмотрении двух этих способов они имеют некоторые отличия в постановке эксперимента. Необходимость двухстороннего подхода при экспериментальной проверке метода вызвана тем, что, как правило, не удаётся получить голограмму, которая бы содержала качественную муаровую картину и создавала качественную интерференционную картину при восстановлении. Причина этой несовместимости заключается

в том, что для получения качественной муаровой картины необходимы низкие пространственные частоты, т.е. её контраст зависит от значения функции передачи модуляции фотоматериала, в то время как для качественного восстановленного изображения требования к несущей частоте другие. Получение интерферограмм в виде муаровых картин диктовалось желанием значительно упростить процесс за счет исключения этапа восстановления.

В этом случае в основу голограммного интерферометра была положена схема Маха-Цендера (рис.3). Её выбор вызван тем, что она

Рис.3. Схема установки типа Маха-Цендера:

1 - коллиматор; 2, 5 - полупрозрачные пластинки; 3, 4- зеркала; 6 - линза; 7 - объект; 8 - пластинка оконного стекла; 9-клин; 10-голограмма.

позволяет обеспечить низкую пространственную частоту, сохранив возможность введения объектива необходимой аппаратуры и фокусного расстояния. Объектив введён для получения на голограмме изображения предмета (в нашем случае это электроды), а не дифракционной картины, что значительно упрощает расшифровку интерферограммы. Причём для удобства расшифровки масштаб изображения делался 1:1. В качестве объекта использован тепловой поток, созданный разогретой электрическим током проволокой. В плечо сравнения вводился

оптический клин с небольшим преломляющим углом. Как следует из теоретического рассмотрения метода, для получения интерферограмм с удвоенной чувствительностью необходимо создать пространственные частоты, соответствующие значениям углов, удовлетворяющих неравенству (16). С этой целью проводилась предварительная градуировка барабана поворотного столика, на котором крепился клин. Необходимые пространственные частоты выбирались по градуировочному графику. Основное требование, предъявляемое к установке клина, состоит в том, чтобы он не находился в минимуме отклонения при съёмке с углом голографирования α₀. Градуировка клина и выбор необходимой ориентации полос проводились до введения объектива в схему. При этом пространственная частота составляла 15-20 лин/мм. Для того, чтобы избежать появления высоких пространственных частот при голографировании сферического волнового фронта, возникающего при фокусировке предмета, использован объектив с большим фокусным расстоянием. Как наиболее оптимальной для получения муарограмм, использована фотоплёнка Микрат-300. Она выбрана ввиду того, что из всех отечественных (серийных) высоко разрешающих слоев обладает большим коэффициентом контрастности (γ = 5,4), которую, в свою очередь, определяет видимость муаровой картины. Применение этой фотоплёнки и длиннофокусного объектива позволило сохранить приемлемую видимость картины по всему полю.

На рис.4а представлена интерферограмма исследуемой неоднородности^*, выполненная обычным голографическим методом. Эффект удвоения чувствительности демонстрируется интерферограммами (муаровые картины) рис.4в, г, которые соответствуют той же неоднородности.

Как отмечено выше, рассмотренный метод позволяет компенсировать аберрации, вносимые элементами схемы.

Для демонстрации компенсирующего действия метода голографической интерферометрии с повышенной чувствительностью в рабочую ветвь интерферометра вводилась пластина оконного стекла.

 

Рис.4. Интерферограммы фазовой неоднородности:

а - обычная двухлучевая интерферограмма нагретой проволоки;

б - интерферограмма пластинки оконного стекла;

в - трёхлучевая интерферограмма (муарограмма) в полосах конечной ширины той же неоднородности, что и в (а);

г - трёхлучевая иптерферограмма (муарограмма) в полосах бесконечной ширины.

 

 

 

 

 

 

 

Искажения, вносимые этой пластиной, значительно превосходили искажения, вызванные исследуемым объектом. Интерференционная картина стеклянной пластинки представлена на рис.4б. Как видно из рис.4в,г, её несовершенство не проявляется в модуляции интерференционных полос от исследуемой неоднородности.

Как следует из эксперимента, муарограммы, получаемые при реализации этого метода, позволяет сохранить оперативность обычной интерферометрии при сохранении преимуществ голографической интерферометрии.

Для наблюдения эффекта увеличения чувствительности при восстановлении упомянутых волн тройная экспозиция выполнялась на обычной схеме голографического интерферометра (рис.5). В ней, как и в предыдущей, проводилось голографирование фокусированиого изображения. Использование фокусировки на предмет диктовались желанием устранить появление трех изображений предмета, соответствующих различным углам голографирования. Причём появление трех изображений наблюдалось даже в том случае, когда он убирался при голографировании пучков сравнения, хотя изображения были менее интенсивными. В данном случае голографирование выполялось на фотопластинах Микрат-ВР. В отличие от предыдущего эксперимента, здесь фокусное расстояние линзы и масштаб изображения предмета могут выбираться в широких пределах. Различные углы голографирования пучков сравнения получались также с помощью оптического клина.

Рис.5. Схема обычной голографической установки для получения трёхлучевых интерферограмм:

1 - призма; 2, 3 - зеркала; 4 - линза;

5 - клин; 6 - голограмма; 7 - объект.

На рис.6 представлена интерферограмма той же неоднородности, полученная при восстановлении. Сравнение рис.4а и 6 показывает увеличение фазового сдвига, вносимого объектом, в два раза.

Несмотря на то, что реализация данного метода с помощью трёх экс-позиций на является единственным средством получения подобных интерферограмм, её использование наиболее просто и надёжно.

Рис.6. Трёхлучевая интерферограмма той же неоднородности, что и на рис.4а, полученная при восстановлении.

 

2. Повышение чувствительности при голографировании с ислользованием нескольких длин волн

Для повышения чувствительности голографической интерферометрии можно использовать ОКГ, работающие с излучением нескольких длин волн. Появляющиеся промышленные образцы таких генераторов уже сейчас позволяют иметь сравнительно большой набор длин волн, варьируя которыми, можно управлять чувствительностью голографической интерферометрии как в сторону её повышения, так и понижения.

Метод заключается в том, что вначале голографируют пучок сравнения С в одном цвете λ₀, при угле голографирования α₀ (рис.7), фотопластинку проявляют, закрепляют и устанавливают на прежнее место. Затем голограмму освещают как объектным S, так и опорным О лучками в двух цветах: λ₁ и λ₂ (рис.8).

При этом за голограммой возникают две интерферограммы, соответствующие λ₁ и λ₂. При определённом угле α' между пучками S и О смещения интерференционных полос, вызванные оптической неоднородностью в двух интерферограммах, соответствующих λ₁ и λ₂, будут происходить в противоположных направлениях (рис.8б). Поэтому муаровая картина, возникающая в результате наложения этих двух интерферограмм, будет идентична интерферограмме с удвоенным смещением полос. Это эквивалентно повышению чувствительности в 2 раза.

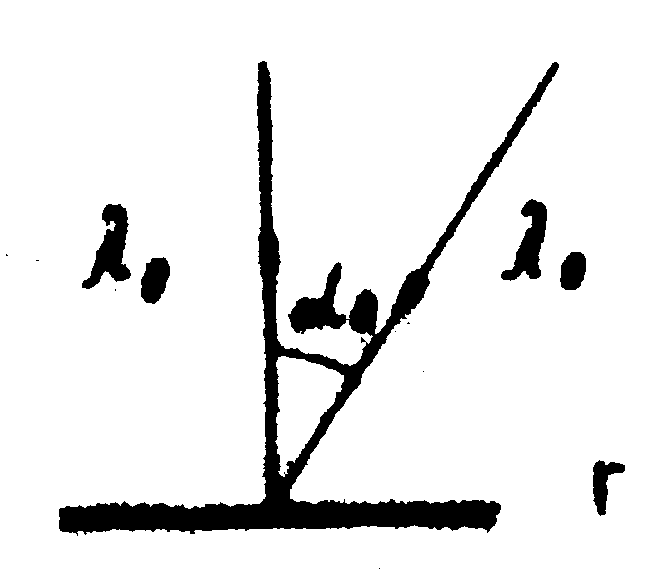
Рис.7. Схема голографирования:

С- пучок сравнения; О- опорный пучок;

Г- голограмма; λ₀- длина волны света.

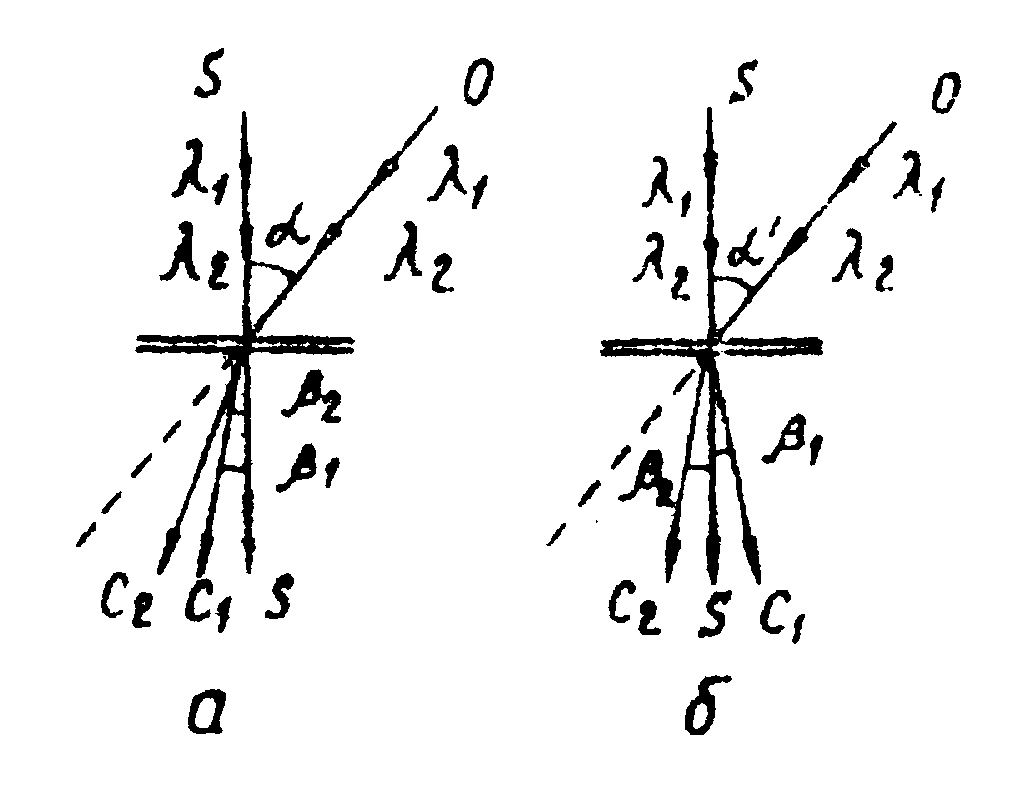
Рис.8. Схемы для наблюдения интерференционных картин,

соответствующих случаю:

а) уменьшении чувствительности;

б) увечичения чувствительности.

С₁ и С₂ - пучки сравнения, восстановленные в длинах волн λ₁ и λ₂ соответственно;

β₁, β₂ - углы дифракции волны С₁ и С₂;

α₁, α₂ - углы восстановления; S - объектный пучок.

Покажем аналитически справедливость вышеприведенного утверждения. Не ограничивая общность, для простота рассуждений будем полагать, что при голографировании используются плоские волна, объектом является прозрачная неоднородность и плоскость голограммы совладает с фронтом волны пучка сравнения и сигнального пучка.

Обозначим комплексные амплитуды волн пучка сравнения и опорного пучка при гологоафировании через Е_с и Е₀.

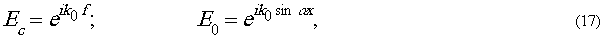
где k₀=2π/λ₀; λ₀ - длина волны света при голографировании; k₀f -фазовые искажения, вносимые оптикой, зависящие от кооринат x и y, выбранных в плоскости голограимы; α₀ - угол голографирования.

Распределение интенсивности на голограмме будет:

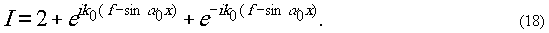
Предположим, что амплитудное пропускание голограммы удовлетворяет уравнению

T_a=cI.

Осветим эту голограмму опорным (O₁) и объектным (S₁) пучками с длиной волны λ₁, комплексные амплитуды которых

где α - угол между пучками О₁ и S₂; k₁f_s - искажения фазы, вызванные исследуемой неоднородностью. Если α≈α₀ то за голограммой в направлении нормали будут распространяться волны:

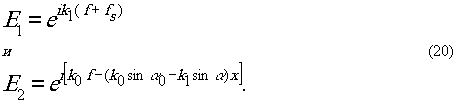
Из (20) найдём уравнение интерферограммы для длины волны λ₁:

I₁=|E₁+E₂|²=5+4cosФ₁, (21)

где

Ф₁=f(k₁-k₀)+k₁f_s+(k₀sinα₀-k₁sinα)x.

Такое же выражение можно написать для случая освещения голограммы с длиной волны λ₂

I₂=5+4cosФ₂, (22)

где

Ф₂=f(k₂-k₀)+k₂f_s+(k₀sinα₀-k₂sinα)x.

При одновременном освещении голограммы излучением с длинами волн λ₁ и λ₂ получим некогерентное наложение двух интерферограмм I₁ и I₂, которое даёт муаровую картину:

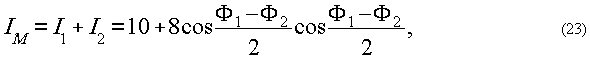
где

Ф_i=f(k_i-k₀)+k_if_s+k_isinβ_ix,

а k_isinβ_i=k₀sinα₀-k_isinα. β - угол дифракции, i = 1, 2.

Тогда

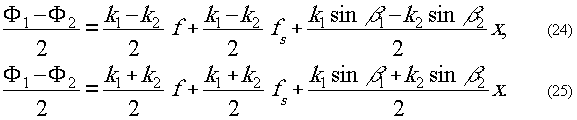
Какое из этих двух соотношений (24 и 25) определяет фазу несущей, какое - фазу муаровых полос, зависит от того, будут ли β₁ и β₂ одинакового или противоположного знака. А это, в свою очередь, определяется величиной α (при данных k₀, α₀, k₁ и k₂). Рассмотрим эти два случая раздельно,

Случай 1. Величина α выбрана так, что β₁ и β₂ имеют одинаковый знак (рис.8а). В этом случае фаза несущей определяется уравнением (25), а фаза муаровых полос - уравнением (24).

Сдвиг фазы (смещение муаровых полос), обусловленное оптической неоднородностью исследуемого объекта и аберрациями оптики, определяется членами, содержащие соответственно f_s и f. Получаемая при этом муаровая картина идентична, интерферограмме, снятой со светом, волновое число которого

k=k₁-k₂. (26)

Эта методика может быть полезна там, где требуется существенное уменьшение чувствительности интерферометрического метода, например, для идентификации полос при наличии в исследуемом объекте скачков плотности. Как видно из (24), в рассматриваемом случае аберрации, вносимые оптикой, не исключаются.

Случай 2. Величина α выбрана так, что β₁ и β₂ противоположного знака (рис.8б). В этом случае (24) определяет фазу несущей, а (25) - фазу муаровых полос. Здесь муаровая картина идентична интерферограмме, полученной со светом, волновое число которого

k=k₁+k₂. (26)

Поэтому этот случай представляет интерес с точки зрения повышения чувствительности голографической интерферометрии. При k₁≈k₂

имеем k≈2k₁ , что эквивалентно повышению чувствительности в два раза. Как видно из (25), и в этом случае аберрации, вносимые опти-

кой, не исключаются. Однако при соответствующем подборе k₀, k₁ и k₂ вклад этих аберраций может быть значительно уменьшен и сведён к нулю при

k₁+k₂=2k₀. (28)

Период муаровых полос в рассматриваемом случае определяется из выражения:

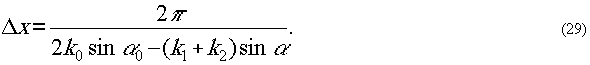
Меняя угол α, можно изменять Δx в широких пределах. В частности, при

Δυ=∞. В этом случае полученная картина идентична интерферограмме в полосах бесконечной ширины.

Таким образом, трёхцветная голографическая интерферометрия позволяет получать интерферограммы как с повышенной, так и пониженной (на много порядков величины) чувствительностью. При повышении чувствительности имеется возможность получить картины интерференции в полосах как конечной, так и бесконечной ширины. Кроме того, поскольку методика предусматривает предварительное голографирование пучка сравнения, интерферограмма исследуемой неоднородности получается в реальном масштабе времени, т.е. методика может быть применена для исследования быстропротекающих процессов.

Интерферограммы с уменьшенной или увеличенной чувствительностью можно получить не только в виде муаровых картин, как это рассмотрено выше, но и эа счёт непосредственного взаимодействия восстановленных волн. При этом уменьшение чувствительности будет основываться на том же принципе: волновые фронты от источников с различными длинами волн претерпевают различную деформацию при прохождении через один и тот же объект.

Как рассмотрено выше, механизм образования интерференционной картины с той или иной чувствительностью состоит во взаимодействии двух структур, каждая из которых представляет собой интерференционную картину в полосах конечной ширины в соответствующем

цвете. В первом случае деформации полос за счёт исследуемой неоднородности имеет одинаковые знаки для обеих структур, во втором случае сравниваются структуры с противоположными знаками.

Между описанными и нижеследующими методами сохраняется полная аналогия, если от взаимодействии соответствующих структур перейти к взаимодействию волновых фронтов, а именно: если сравнивать волновые фронты, имеющие одинаковый знак деформации, но различную величину, или сравнивать волновые фронты, имеющие разные знаки деформации с тем же отличием в величинах.

Рассмотрим эти случаи и возможные схемы их реализации. Пусть комплексные амплитуды волн двухцветного когерентного источника после прохождения объекта характеризуются распределением фаз φ₁ и φ₂ и задаются в виде:

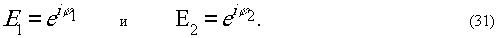
Предположим, что опорные пучки двух цветов падают на фотопластинку под различными углами α₁ и α₂, лежащими в одной плоскости, как показано на рис.9а. При этом их комплексные амплитуды будут:

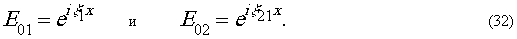
Распределение интенсивности, которое создаётся на фотопластинке, опишется двумя уравнениями, соответствующими акспонированию на двух длинах волн: λ₁ и λ₂.

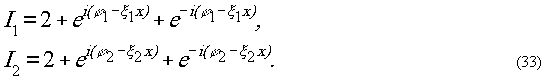
Если углы голографирования подобраны так, что ξ₁=ξ₂, то освещенне голограммы одним из опорных пучков приведёт к появлению интерференционной картины, в которой распределение интенсивности будет соответствовать уравнению:

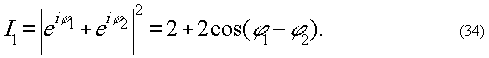
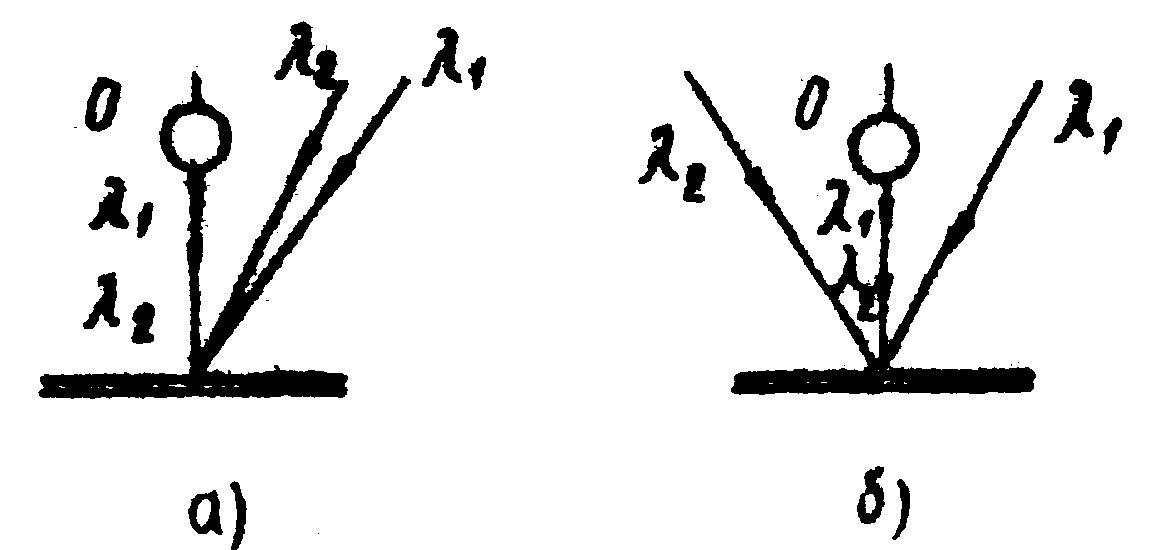
Рис.9. Принципиальные схемы двухцветного голографирования для получения интерферограмм:

а - с пониженной чувствительностью,

б - с повышенной чувствительностью;

О - объект.

Следуя введенным обозначениям, аргумент в выраяении (З^) можно представить в виде:

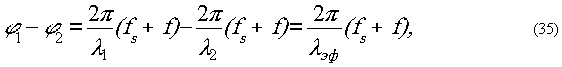
где λ_эф - эффективная длина волны, которой соответствует данная интерференционная картина и которая определяется используемыми при голографировании длинами волн как:

Таким образом, данная мнтерферограмма будет равносильна той, которую можно получить на длине волны, в несколько раз большей.

Такое же решение вопроса уменьшения чувствительности предлагается в работе /2/^*.

Реализация рассмотренного метода происходила по схеме, изображенной на pиc.10. Выбор этой схемы, которая обычно используется для ахроматизации интерференционных полос, вызван желанием получить одинаковые пространственные частоты при голографировании с разными длинами волн. При голографировании использованы излучения двух ОКГ с длинами волн λ₁=632,8 нм и λ₁=488,0 нм, которые

 

предварительно коллимировались и затем диспергировали на дифракционной решётке 1. Объектив 2 создавал изображение решётки в позиции 4, где помещалась фотопластинка. Диафрагма 5 устраняла неиспользуемые порядки дифракции.

Объект - неоднородность, созданная пламеней спиртовки - помещался в прямопроходяцем пучке. Голографирование проводилось однократным экспонированием, при этом интенсивности излучений двух ОКГ обеспечивали одинаковые почернения фотопластинки за время экспозиции.

На рис.11б прицелена интерферограмма исследуемого объекта полученная при восстановлении с голограммы, выполненной с использованием двух длин волн. Для сравнения приведена интерферограмма той же неоднородности, поученная на длине волны 632,8 нм (рисунок 11а). Как видно из рисунков, обе интерферограммы находятся в полном соответствии, если учесть, что эффективная длина волны составила 3,4·632,8 нм.

Случай, приводящий к увеличению чувствительности при двухцветной голографировании, будет иметь место, если осуществить наложение восстановленных волн с разными знаками деформации волнового фронта, т.е. если взаимодействуют мнимая и действительная волны, восстановленные за счёт голографирования с длинами волн λ₁, и λ₂ (см. также /2/). При этом эффективная длина волны, которой соответствует интерференционная картина при восстановлении,будет определяться уравнением:

Данный метод аналогичен трехлучевому методу /5/, но коэффициент увеличения чувствительности в нём не равен 2, а зависит от используемых длин волн:

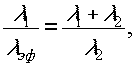
если сравниваются интерферограммы на длинах волн λ₁ и λ_эф.

Принципиальная схема голографирования для этого случая изображена на рис.9б. При её реализации наиболее удобна схема, показанная на рис.10, с тем лишь отличием, что опорные пучки созда-

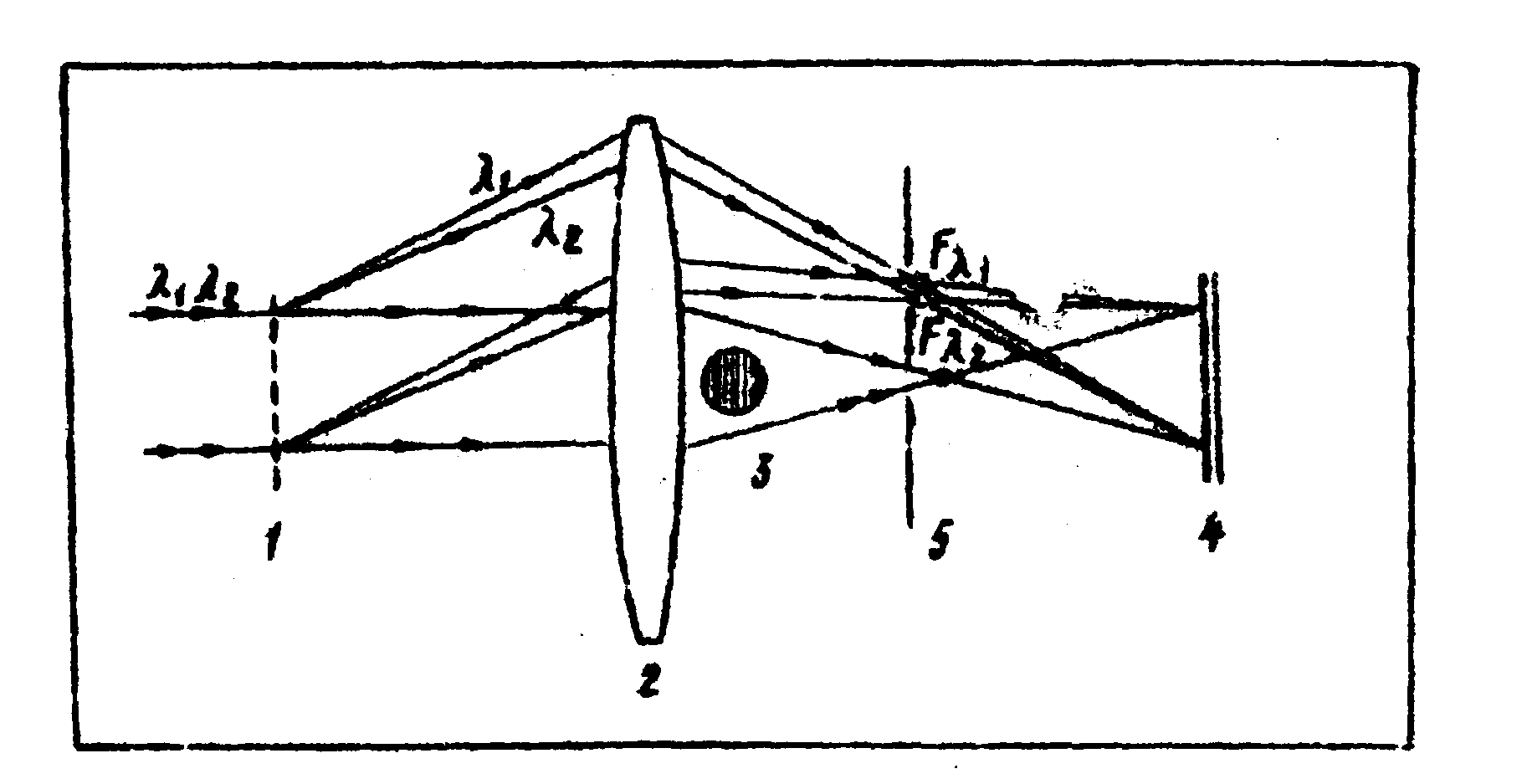
Рис.10. Оптическая схема установки, собранной

по принципиальной схеме рис.9а:

1 - дифракционная решётка; 2 - объектив; 3 - объект;

4 - фотопластинка; 5-диафрагма.

 

 

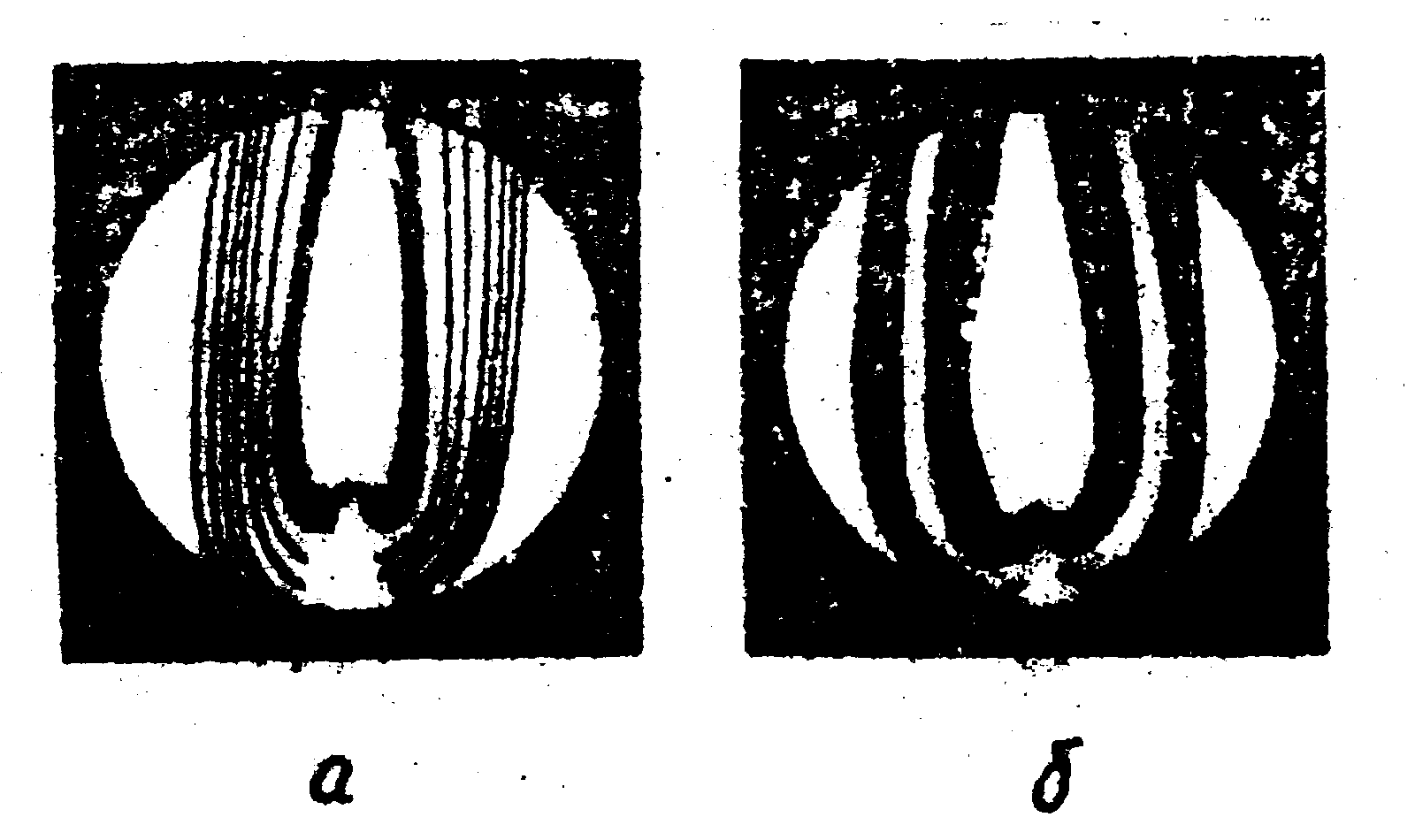
Рис.11. Интерферограммы пламени спиртовки, полученные при

восстановлении в случае:

а - одноцветного голографирования,

б - двухцветного голографирования.

 

 

 

 

ются первым и минус первым порядком дифракции и каждый иа них образован светом с одной длиной волны. Как и в предыдущем методе,

здесь экспонирование однократное, восстановление - светом одной длины волны.

3. Использование нелинейных эффектов

в голографической интерферометрии

Вопрос об использовании нелинейного эффекта в голограммной интерферометрии рассматривался автором на нескольких семинарах и частично отражён в их материалах. Этой теме посвящена и работа /3/ хотя и в виде краткого сообщения. Здесь будет дано более полное изложение метода, указаны оптимальные условия при его реализации, рассмотрены преимущества и недостатки, а также предел его применения. Для иллюстрации в работе приведены экспериментальные результаты .

Для рассмотрения сущности метода обозначим через Е_s и E₀, комплексные амплитуды объектного и опорного пучков при голографировании (рис.12а)

E_s=e^iφ, E₀=e^iξx, (38)

где φ характеризует распределение фаз, созданное объектом, и является функцией координат х, y голограимы, 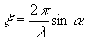Распределение интенсивности в плоскости фотопластины будет:

I=2[1+Cos(φ-ξx)]. (39)

Как известно, для экспонированного фотослоя амплитудное пропускание может быть записано в виде:

где γ- коэффициент контрастности используемого фотоматериала. Подставив (39) в (40) и разложив в ряд по степеням -γ/2, получим уравнение для амплитудного пропускания голограммы:

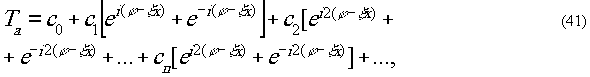
где c_n =(n=1, 2,... ) являются коэффициентами, зависящими от γ и видимости голографируемой интерференционной картины. При освещении голограммы плоскими волнами, образующими ту же пространственную частоту на её поверхности, наблюдают интерференционную картину с распределением интенсивности

I₁=|c₁e^iφ+c₀|²=c₁²+c₀²+2c₁c₀Cosφ. (42)

Это известный способ получения интерферограмм методом регистрации объектного пучка.

При получении подобных интерферограмм не возникает трудностей и выборе условий экспонирования, так как они могут получаться при любых значениях γ. Иными словами, они получаются как при линейном (γ=-2), так и при нелинейном (γ≠-2) соотношениях между амплитудным пропусканием и регистрируемой интенсивностью. Однако если γ≠-2, то освещение голограммы приводит к появлению восстановленных волн в высших порядках дифракции, что подтверждается уравнением (41). При этом в n -ом порядке дифракции восстановится волна о амплитудой Е_sn= е^inφ, в которой фазовые возмущения в n раз больше по отношению к исходной волне. Следовательно, если на плоскую волну сравнения накладывать волну, восстановленную в n-ом порядке дифракции, то полученная интерферограмма будет в n раз чувствительнее к изменениям фазы. Уравнение для распределения интенсивности в этой интерференционной картине будет:

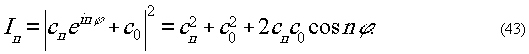
Сравнение (42) и (43) показывает, что в последнем случае фаза изменяется в n раз быстрее, т.е. записанная на голограмме неоднородность представится интерференционной картиной с частотой полос в n раз большей. Получить наложение упомянутых волн можно

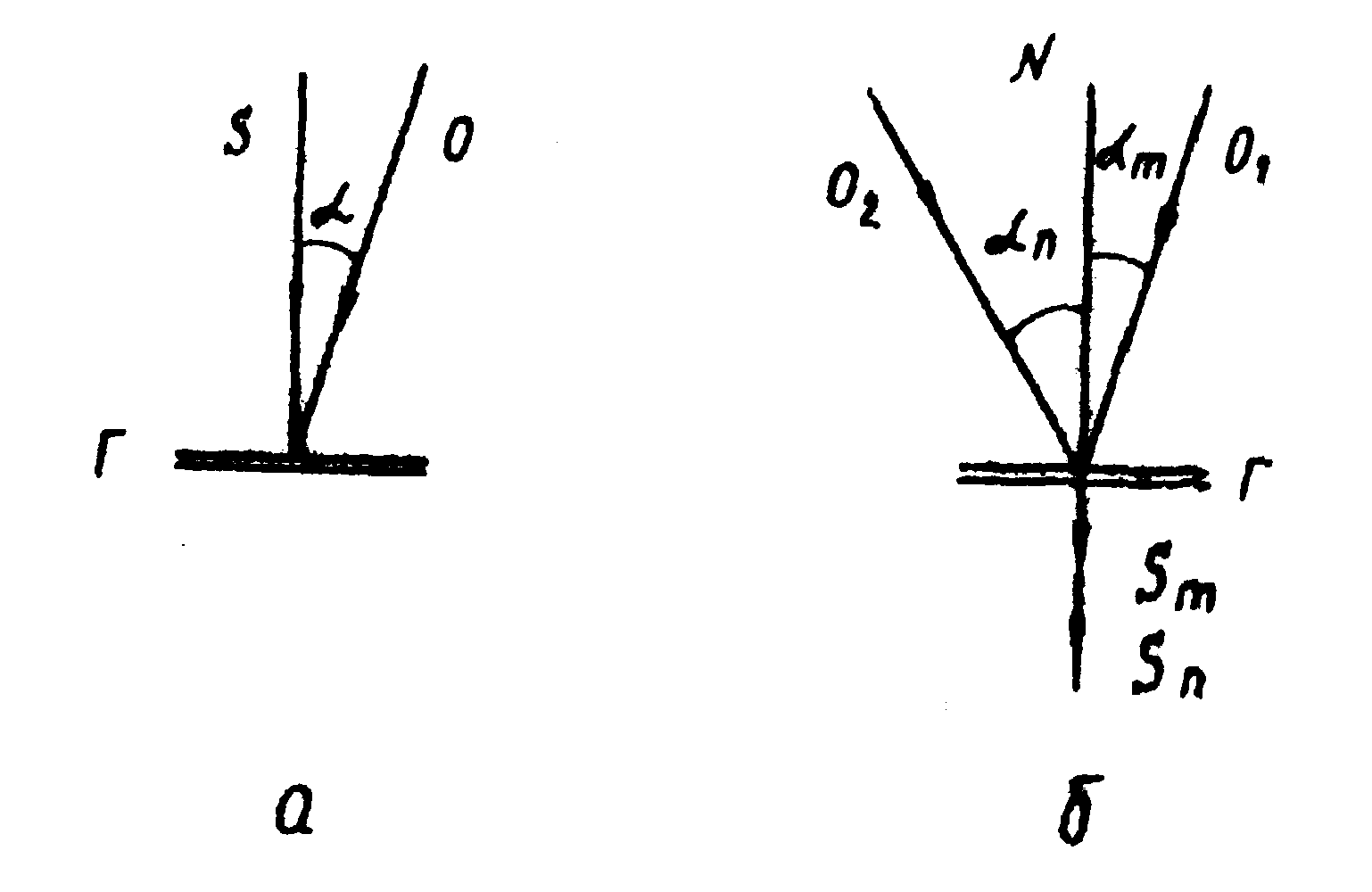
Рис.12. Принципиальная схема голографирования (а) и получения интерферограмм (б) с использованием высших порядков дифракции:

S и O - объективный и опорный пучки при голографировании; Г- голограмма; α - угол голографирования; α_m, α_n - углы, образованные восстанавливающими пучками O₁ и О₂ с нормалью N; S_m и S_n - восстановленные пучки в m-ом и n-ом порядках дифракции.

при освещении голограммы плоскими воkнами, одна из которых распространяется вдоль нормали N, другая образует с первой угол

α_n(α_n=arcsin(nsinα)).

Видимость (W) наблюдаемой интерференционной картины определяется в данчом случае величинами С₀ и С_n :

Причём w=1 при С_n=С₀. Ввиду уменьшения С_n, с ростом n приемлемую видимость интерференционной картины можно сохранить соответствующим подбором интенсивностей пучков при освещении голограммы или использованием метода, описанного в /4/.

Увеличение чувствительности можно получить также при наложении волн, принадлежащих различным порядкам, например при использовании восстановленных волн m-ого и n-ого порядков дифракции. При этом необходимо освещать голограмму плоскими волнами с амплитудами

Е₀₁= е^imξx и Е₀₂= е^inξx. В этом случае интерференционная картина, наблюдаемая, например, в направлении нормали к плоскости голограммы, будет соответствовать уравнению:

I_nm=|c_me^imφ+c_-ne^-inφ|²=c_m²+c²_-n+2c_nc_mcos[(m+n) φ]. (45)

Для обеспечения оптимальной видимости интерференционных полос значения с_m и с_-n должны быть по возможности близкими по величине. очевидно, что максимальная видимость интерференционных полос будет иметь место в случае, когда используются сопряжённые волны одного порядка (-n=m), так как их амплитуды равны.

В частном случае,при m=-n= I, уравнение (45) представляет собой интерферограмму, соответствующую наложению действительной и мнимой волн от исследуемого объекта. Она идентична интерферограмме, получаемой методом трёхлучевой голографической интерферометрии /5/.

Для получения интерферограмм типа (45) голограмму необходимо освещать двумя опорными пучками (рис.126) так, чтобы углы α_n и α_m удовлетворяли условию

sinα_n = n sinα; sinα_m = m sinα. (46)

Как следует из (46), пространственные частоты, образуемые освещающими пучками, должны быть кратными несущей частоты самой голограммы. В этом случае наблюдается интерференционная картина в полосах бесконечной ширины.

Если же уравнения (9) не выполняются, то наблюдается картина интерференции в полосах конечной ширины.

При реализации рассмотренных способов получения интерферограмм с повышенной чувствительностью использовалась обычная схема голограммного интерферометра. Для нелинейной записи исследуемого волнового фронта были использованы: низкая пространственная частота При голографировании, фотоматериал с большим коэффициентом контрастности (Микрат-300, γ= 5,4) и равенство интенсивностей опорного и сигнального пучков. Плавная подстройка пространственных частот при освещении голограммы производилась вращением клина во-

круг преломляющего ребра. При восстановлении и голографировании использовалось излучение ОКГ с длиной волны 632,8 нм. На рис.13 приведены нитерферограммы пламени спиртовки, полученные из одной и той же голограммы при различных условиях её освещения. Как и следовало ожидать, число полос на рис.13б, в, г увеличено в 2, 3 и 4 раза, соответственно, по отношению к интерференционной картине рис.13а. Это эквивалентно уменьшению длины волны, на которой проводится интерференционный анализ. В рассмотренных интерферограммах этими длинами волн должны быть: 632,8 нм, 366,4 нм, 210,8 нм и 158,2 нм соответственно. Таким образом, обходя трудности, связанные с использованием коротких длин волн в интерференционном анализе, голограммная интерферометрия создает простую апостериорную возможность значительного повышения чувствительности.

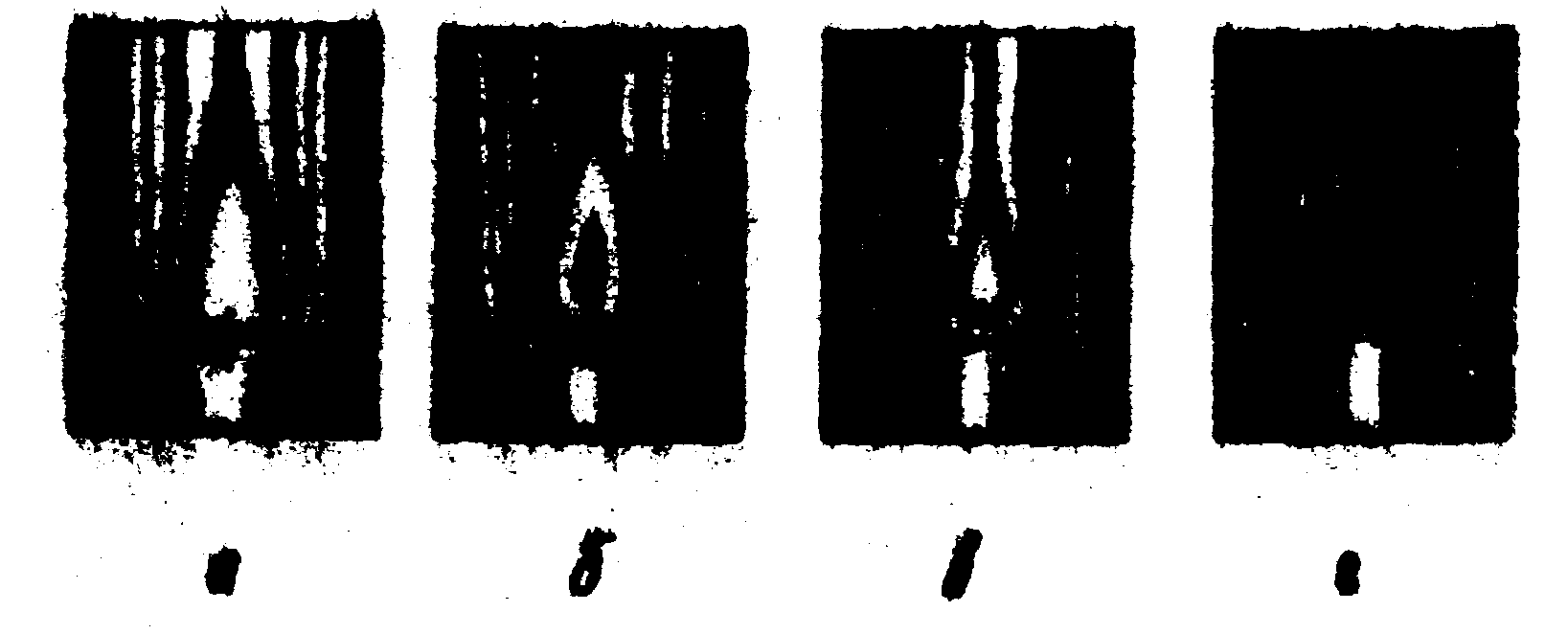
Рис.13. Интерферограммы пламени спиртовки, полученные из одной и той же голограммы

а) n=0, m=1 (обычная интерферограмма);

б) -n=m=1; в) -n =1, m=2;

г) -n=m=2.

Описанная выше методика не лишена и своих недостатков, к которым следует отнести спад интенсивности волн, восстанавливаемых в высших порядках дифракции, аберрации голограмм (при использовании сферических волн), отсутствие компенсации искажений, вносимых некачественными элементами схемы. Поэтому на практике приходится ограничиваться небольшими значениями n . Частичное устранение перечисленных недостатков может производиться выбором опти-

мальных условий при голографировании и восстановлении, а также при выборе используемого фотоматериала. Как наиболее благоприятными, можно рекомендовать следующие условия: использование низких пространственных частот, высокоразрешающих фотоматериалов с большим коэффициентом контрастности и малой усадкой, а также использование сравнительно качественных оптических элементов схемы. Оценка показывает, что аберрации голограммы зависят от самой исследуемой неоднородности. С этой точки зрения аберрации будут минимальными при исследовании слабых оптических неоднородностей.

Нелинейные эффекты могут быть использованы и в методе наложения друг на друга двух голограмм, на которых раздельно регистрированы объектная волна и волна сравнения. Для увеличения чувствительности в n раз в этом методе необходимо, чтобы несущая частота голограммы волны сравнения была в n раз больше несущей частоты голограммы объектной волны. Подтверждением этому может служить нижеследующий эксперимент. На рис.14 приведены результаты экспериментов по использованию нелинейных свойств фотоэмульсии для получения муарограмм, представляющих собой интерференционные картины с повышенной чувствительностью. Объект представляя собой клиновидную пластинку, интерференционная картина которой показана на рис.14а. Приведённые муарограммы получены методом

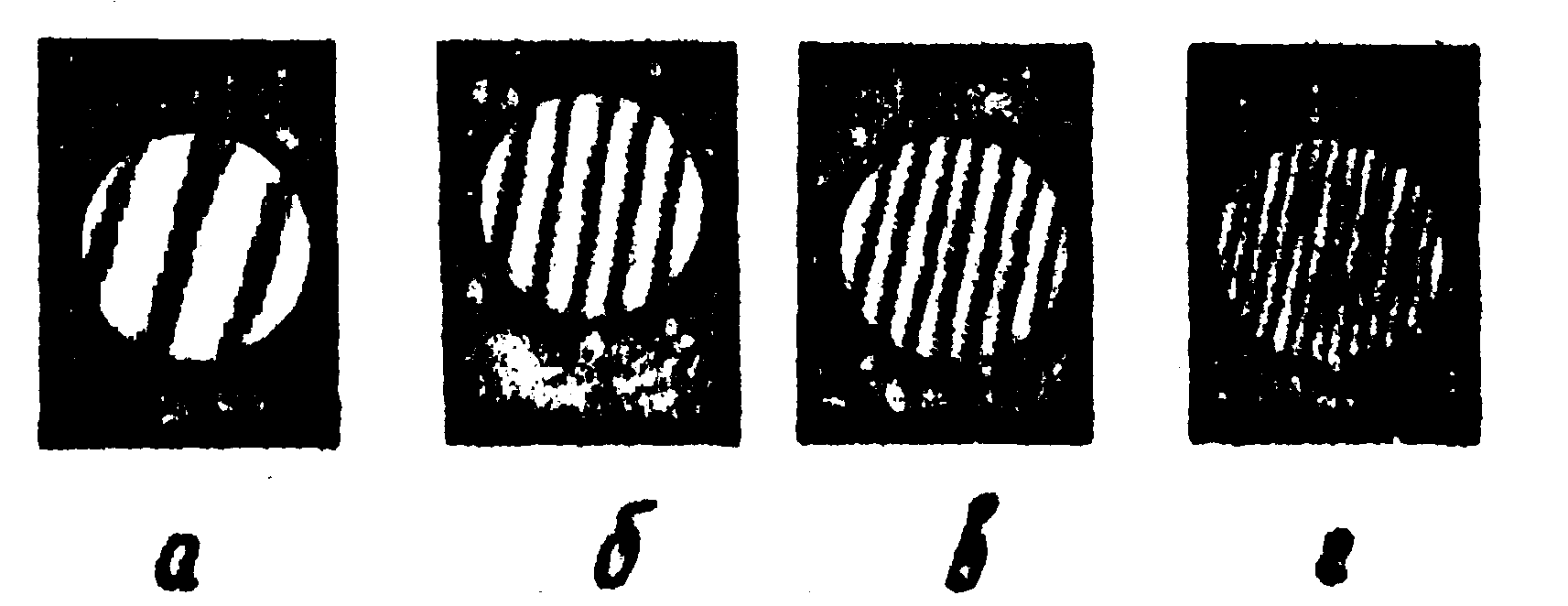
Рис.14. Интерферограммы (муаровые картины) клиновидной пластины, полученные двухкратным экспонированием, где голографирование пучка сравнения выполнено с пространственными частотами:

а -ν₀, б -2 ν₀, в -3 ν₀, г -4 ν₀, где ν₀ - пространственная частота при голографировании исследуемого волнового фронта.

двойной экспозиции, причём пространственные частоты при голографировании были равны 2ν₀, 3ν₀ и 4ν₀ где ν₀ - пространственная частота голографирования исследуемого волнового фронта. Эксперимент проводился на схеме, обычно используемой для ахроматизации интерференционных полос, как наиболее удобной для выполнения условия (46). Очевидно, что подобные интерферограммы можно получить и при восстановлении волн с таких голограмм. Интерференционные картины, наблюдаемые в этом случае будут тождественны тем, которые описываются уравнением (43).

Резюмируя описанные методы, можно отметить, что развитие голографии открывает широкие возможности в управлении чувствительностью интерференционного анализа.

Л и т е р а т у р а

1. К.С.Мустафин, В.А.Селезнев, Е.И.Штырков. Труды ввиолка, выпуск №1233, стр.151 (1968).

2. F.Wegl, O.M.Friedrich and A.A.Daugal, 21 st. Annual Southwestern IEEE Conference, Apriel 1969, San Antonio, Texas.

3. O.Brindahl, A.W.Johmann. JOSA, 58, 1, 141 (1968).

4. P.James Corroll. Appl.Opt., 7, 8, 1642 (1968).

5. De Manoranjan, Leandre Sevigny. Appl.Opt., 6, 10, 1965 (1967).