ГАБОРОВСКИЕ ГОЛОГРАММЫ С ДИФФУЗНОЙ ПОДСВЕТКОЙ ОКЬЕКТОВ
Б.Г.Турухано
В в е д е н и е
После введения наклонного вспомогательного пучка интерес к габоровским однолучевым схемам значительно ослаб, несмотря на ряд очевидных преимуществ последних. Эти было связано с трудностью получения и восстановления голограмм с диффузной подсветкой объектов.
Рассмотрим процесс получения и восстановления габоровской голограммы, которая
отличается тем, что при создании голограммы оси основного и вспомогательного
пучков совпадают, согласно работе Д.Габора /1/. В этой же работе приводится
выражение для волны
us, исходящей
от голограммы при подсветке ее первичной волной 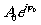 :
:
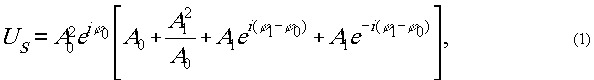
где
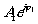 - вторичная волна, обусловленная возмущением, созданным предметов. Третий и
четвёртый члены выражения (1) представляют две волны, соответствующие мнимому
и действительному изображениям исходного объекта. Оба изображения восстанавливаются
по одному направлению, но в разных областях пространства, если положение вспомогательного
источника, соответствующего волне
- вторичная волна, обусловленная возмущением, созданным предметов. Третий и
четвёртый члены выражения (1) представляют две волны, соответствующие мнимому
и действительному изображениям исходного объекта. Оба изображения восстанавливаются
по одному направлению, но в разных областях пространства, если положение вспомогательного
источника, соответствующего волне 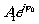 ,
не совпадает с положением объекта. При центральном восстановлении голограммы
мнимое и действительное изображения вносят неравномерный фон друг в друга
/1,2/. Первые два члена при восстановлении
дают плоскую волну. Волна, отвечающая второму члену, вносит неравномерный фон,
обусловленный модуляцией амплитудной частью объектного пучка. Уменьшение этого
фона возможно в том случае, когда интенсивность вспомогательного пучка i
,
не совпадает с положением объекта. При центральном восстановлении голограммы
мнимое и действительное изображения вносят неравномерный фон друг в друга
/1,2/. Первые два члена при восстановлении
дают плоскую волну. Волна, отвечающая второму члену, вносит неравномерный фон,
обусловленный модуляцией амплитудной частью объектного пучка. Уменьшение этого
фона возможно в том случае, когда интенсивность вспомогательного пучка ia
0
относительно велика,т.е.
А
0>А1. (2)
Условие (2) приводит к тому, что при введении когерентного фона на голограмму сквозь сам объект происходит восстановление лишь контрастных частей объекта.
При голографировании контрастных объектов выражение (1) будет справедливо только
для тех участков голограммы, для которых контрастный объект не будет экранировать
вспомогательную волну
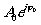 .
Поэтому в общем случае величины А0
и φ0
определяйся структурой объекта и не являются постоянные величинами для всего
поля голограммы. Постановка матового рассеивателя перед объектом полностью нарушит
структуру вспомогательной волны и устранит возможность восстановления.
.
Поэтому в общем случае величины А0
и φ0
определяйся структурой объекта и не являются постоянные величинами для всего
поля голограммы. Постановка матового рассеивателя перед объектом полностью нарушит
структуру вспомогательной волны и устранит возможность восстановления.
В работе /3/ была сделана попытка показать, что габоровская однолучевая схема позволяет не только разделять мнимое и действительное изображения и устранять нежелательный фон, но и использовать диффузную подсветку объекта. Однако для демонстрации этого использовалась оптическая схема изготовления голограммы с прямым опорным пучком. При этом, в отличие от габоровской схемы, центральный луч объектного пучка не совпадал с центральным лучом основного пучка, что приводило к обрезанию ближних порядков дифракции на голограмме. Возможности таких оптических схем рассмотрены в работе /4/.
1.
Получение голограмм
Рассмотрим оптические схемы для получения голограмм Габора с диффузной подсветкой объектов.
А. Простейшая схема с использованием полуматового рассеивателя приведена на рис.1а /5/. При изготовлении рассеивателя выдерживается условие равенства интенсивности рассеянной волны (iр), которая служит для подсветки объектов и интенсивности волны,прошедшей без рассеяния (iв). Величина (iв) является когерентным вспомогательным фоном. Для измерения интенсивности рассеянной волны ip свет, прошедший через рассеиватель, фокусируется и в фокусе линзы измеряется величина iв. Интенсивность рассеянной волны находится как ip=i0-iв,где i0- интенсивность первичного
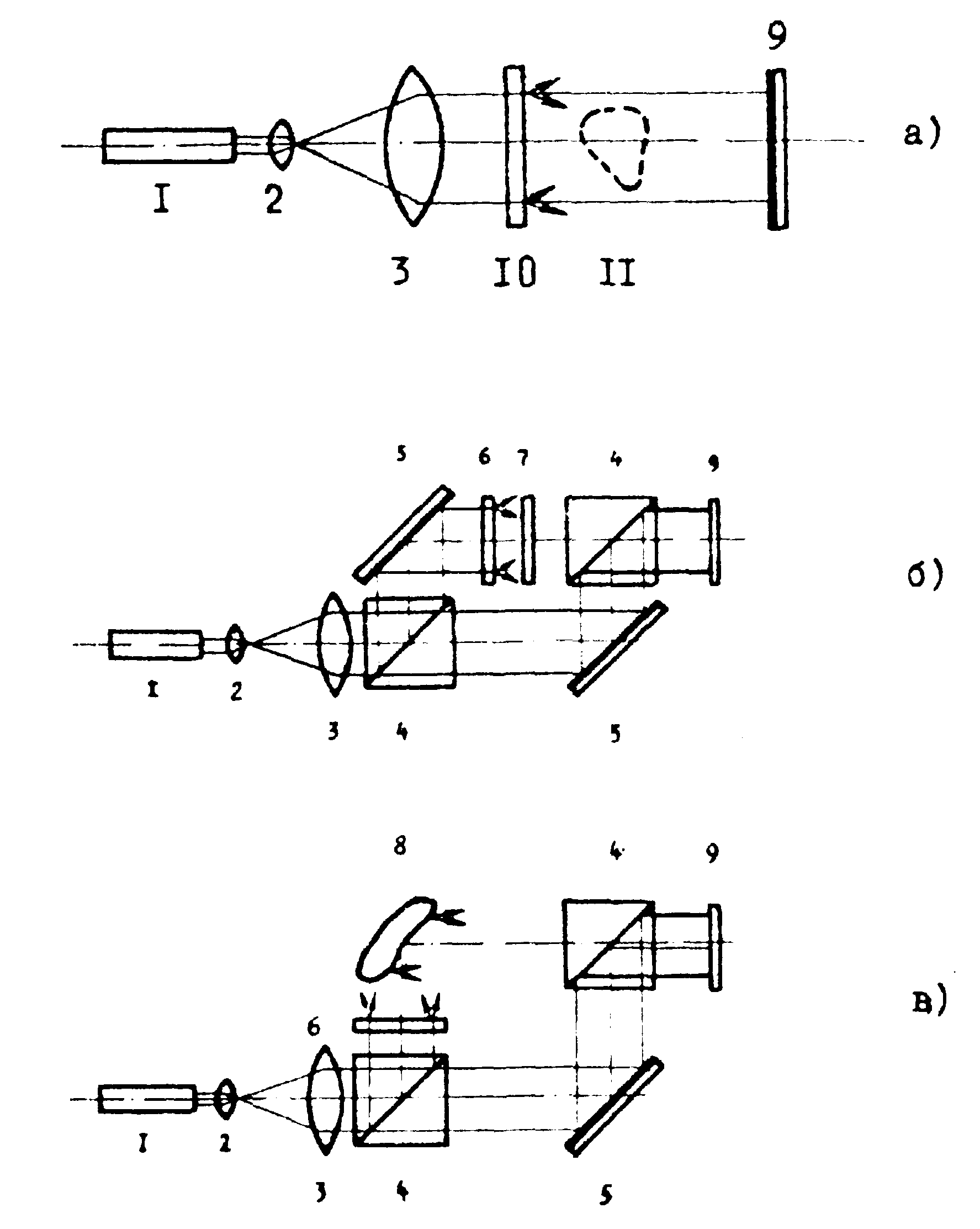
Рис.1. Оптические схемы получения голограмм:
1 - лазер, 2,3 - коллимирующие линзы, 4 - призма-куб, 5 - зеркало, 6 - матовый рассеиватель, 7 - транспарант, 8 - объёмный предмет, 9 - голограмма,10 - полуматовый -рассеиватель, 11 - объект из набора мелких частиц.
пучка света. При этом свет, поглощённый рассеивателем, не учитывается. Соотношение интенсивностей между основной и вспомогательной волнами на голограмме выбирается путём изменения расстояния между рассеивателем и голограммой, так как интенсивность вспомогательной волны практически не зависит от расстояния, а интенсивность рассеянной волны падает с увеличением расстояния.
При голографировании вспомогательный пучок проходит через исследуемый объём, что сужает класс голографируемых объектов. Эта схема применима при голографировании мелких объектов, распределённых по объёму (пузыри треков в пузырьковой камере, туман, аэрозоли и т.п.). Восстановленные изображения объектов видны тёмными на светлом поле (светлопольное изображение)
.
Б. Для тоновых транспарантов и непрозрачных объектов применимы оптические схемы, показанные на рис.1б и 1в, в которых вспомогательный пучок вводится на голограмму, минуя объект /6/. В этом случае амплитуда и фаза ( А
0 и φ0 уравнение (1)) вспомогательного пучка будут постоянными для всего поля голограммы. Для формирования пучков используется схема, аналогичная схеме интерферометра Маха-Цендера. Призмы-куб производят светоделение и совмещение пучков на голограмме. Матовый рассеиватель в схемах (рис.1) позволяет наблюдать визуально восстановленные изображения. Матовый рассеиватель (рис.1в) служит для гашения бликов при голографировании объектов с резким изменением коэффициента отражения. Отметим, что сфокусированные габоровские голограммы описаны Строуком в работе /7/.
2.
Анализ пространственных частот габоровских голограмм с диффузной подсветкой объектов
Для снятия спектра пространственных частот голограмму освещают коллимированным пучком когерентного света и устанавливают в передней фокальной плоскости линзы. Тогда в задней фокальной плоскости образуется спектральное распределение пространственных частот голограммы.
Пусть распределение плотности почернения на голограмме f(x,y),
тогда в задней фокальной плоскости будет преобразование Фурье от функции
f(x,y), т.е. f(ωξ,ωη) /8/:
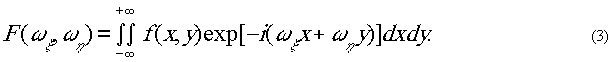
Величины
ωξ и ωη являются частотными координатами, связанными с линейными координатами ξ и η следующим образом:

где λ и
f - длина волны используемого света и фокусное расстояние линзы, осуществляющей преобразование.
Для градуировки частотной плоскости испопьзовзлись голографические дифракционные решётки с известной пространственной частотой
ω. При этом проверялась зависимость координаты в Фурье-плоскости от пространственний частоты ν голографических дифракционных решёток. Как видно из рис.2, аналитическая прямая совпадает с экспериментальными точками до частоты более 500 лин/мм. Этот способ градуировки частотной плоскости компенсирует ряд аберрации преобразующей линзы, такие как астигматизм, кривизну поля и дисторсию.
Регистрация спектров голограмм производилась с помощью установки, оптическая схема которой показана на рис.5. Коллимированный пучок света падает на голограмму (5). В фокальной плоскости линзы (6) записывается её Фурье-спектр. В качестве фотоприёмника используется сканирующий ФЭУ, перед которым устанавливается щелевая диафрагма. Спектр записывается на регистрирующем приборе (8).
В качестве объекта был выбран значок. Габоровская голограмма значка при диффузной подсветке была изготовлена по схеме рис.1в. Сравнивая спектр объекта, при его подсветке сквозь рассеиватель, со спектром габоровской голограммы этого же объекта, можно видеть, что в области нулевых пространственных частот в спектре голограммы выделяется резкий пик (рис.4).
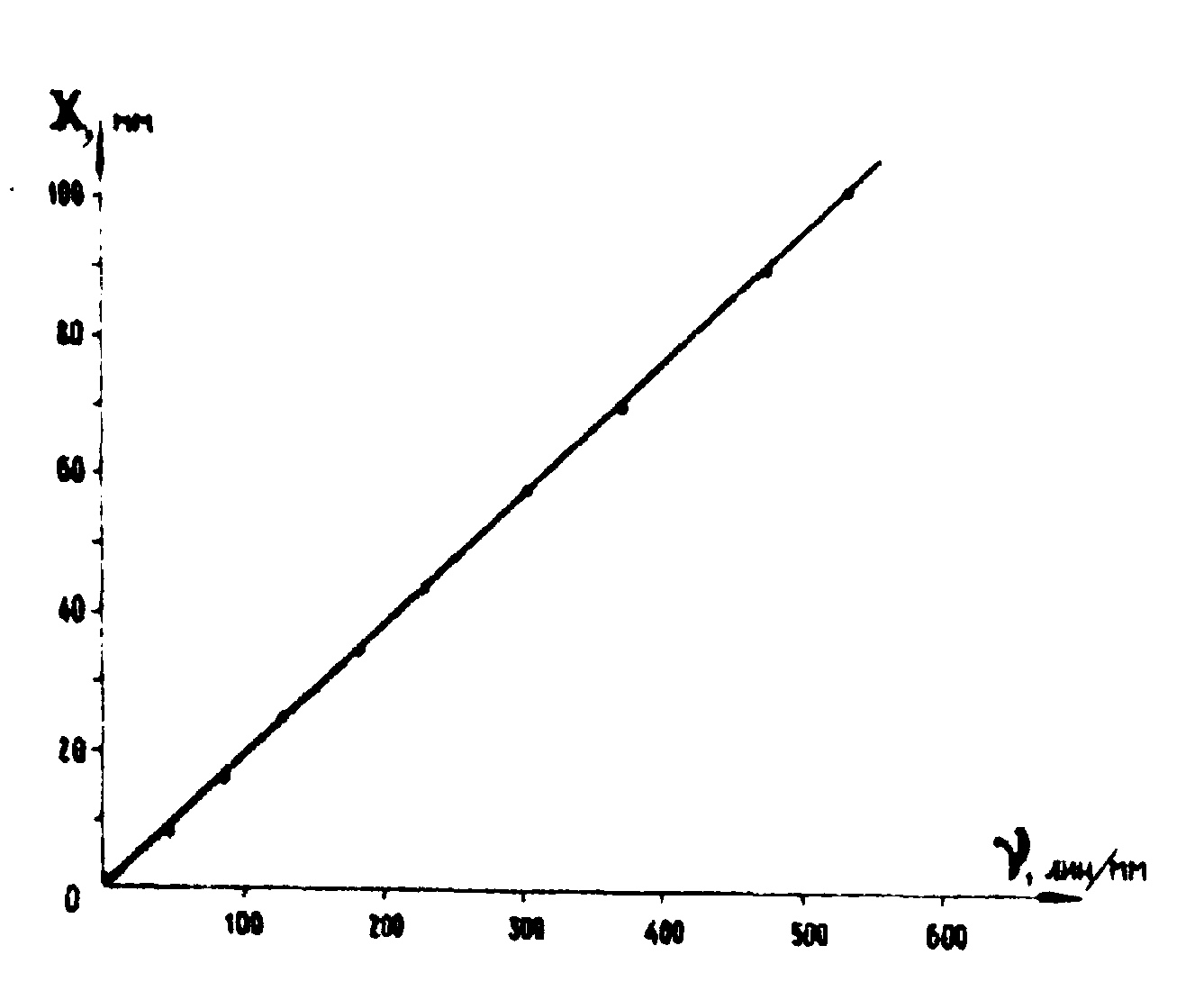
Рис.2.
Зависимость координаты в Фурье-плоскости от пространственной частоты голографических решёток.
Этот пик соответствует первым двум членам уравнения (1), так как эти члены представляют собой плоские волны, которые фокусируются кривой в центральную часть спектра. Поэтому постановка высокочастотного бинарного фильтра вида
t=2kλp
2/d
2 (5)
в центре частотной плоскости позволяет устранить влияние этих членов при восстановлении голограммы.
Из сравнения спектров габоровокой голограымы и голограммы с на-кловныи вспомогательным пучком (рис.5) видно, что верхняя граница пространственных частот голограммы первого типа (рис.5а)
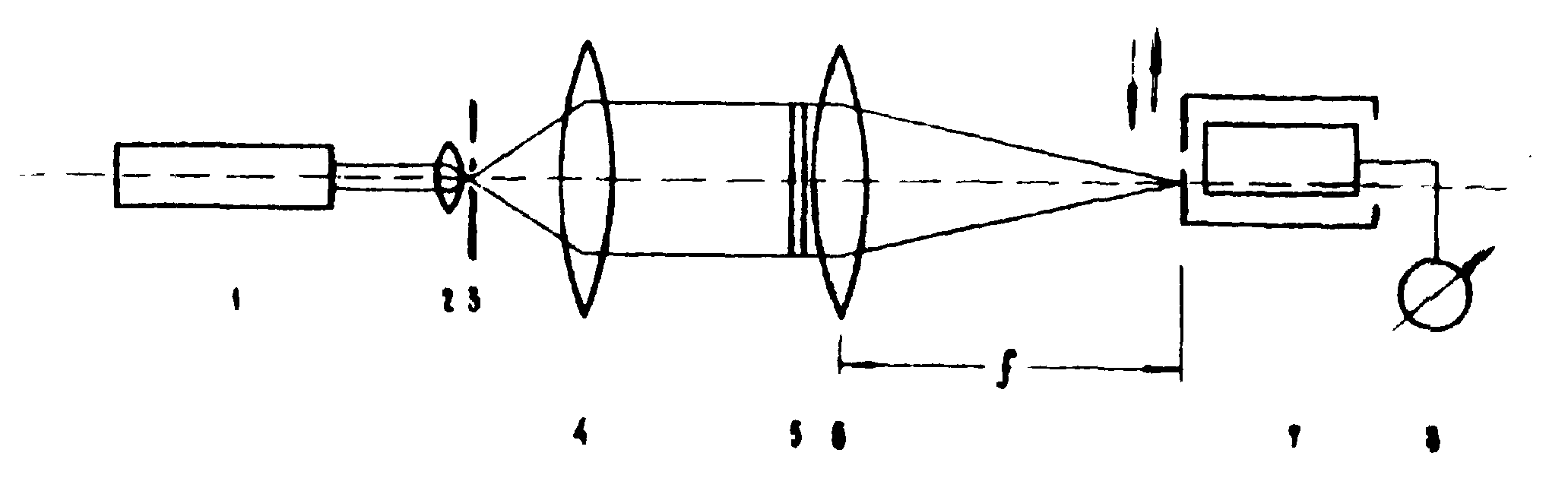
Рис.5. Оптическая схема установки для регистрации спектров голограмм.
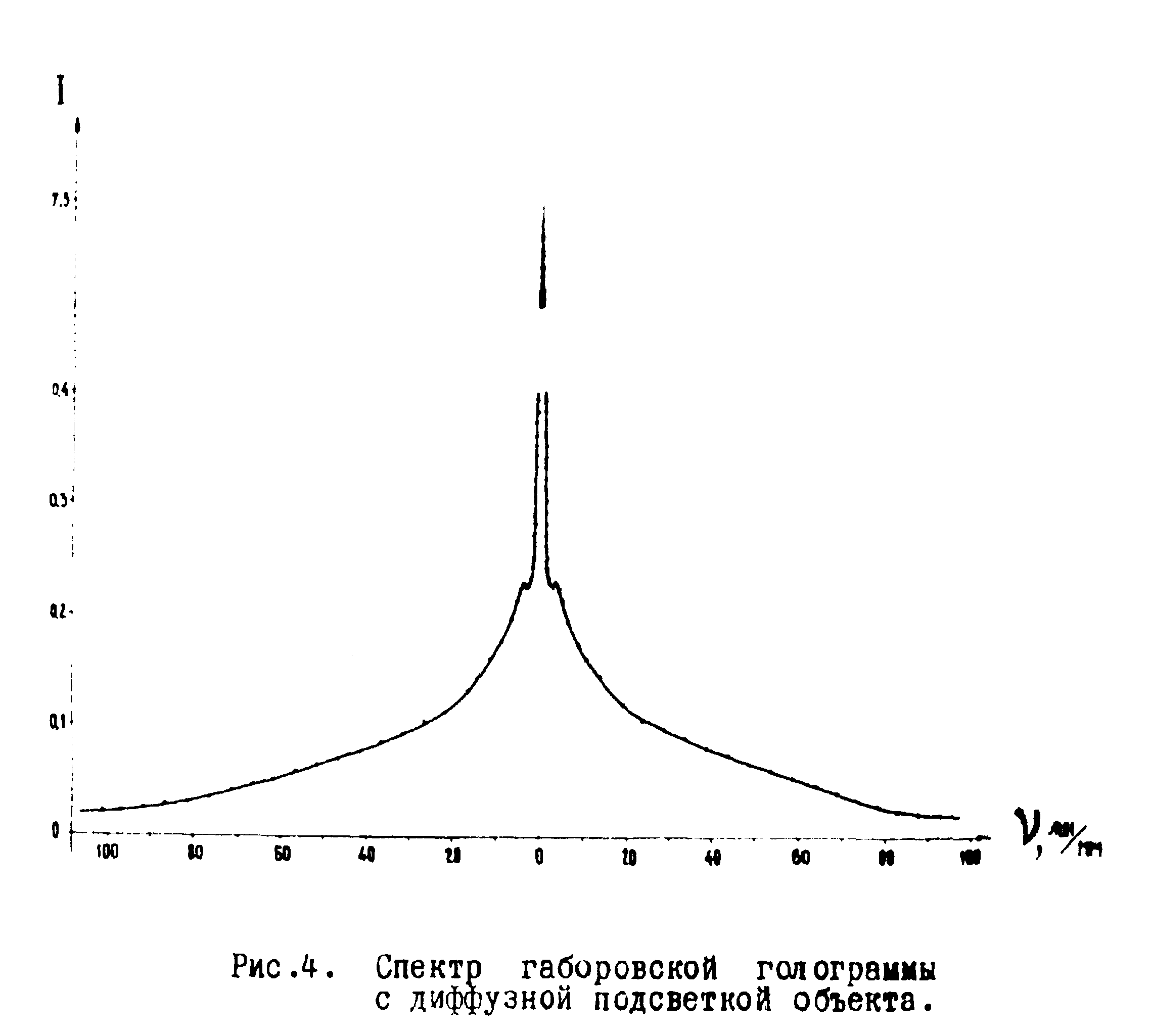
Рис.4. Спектр габоровской голограммы с диффузной подсветкой объекта.
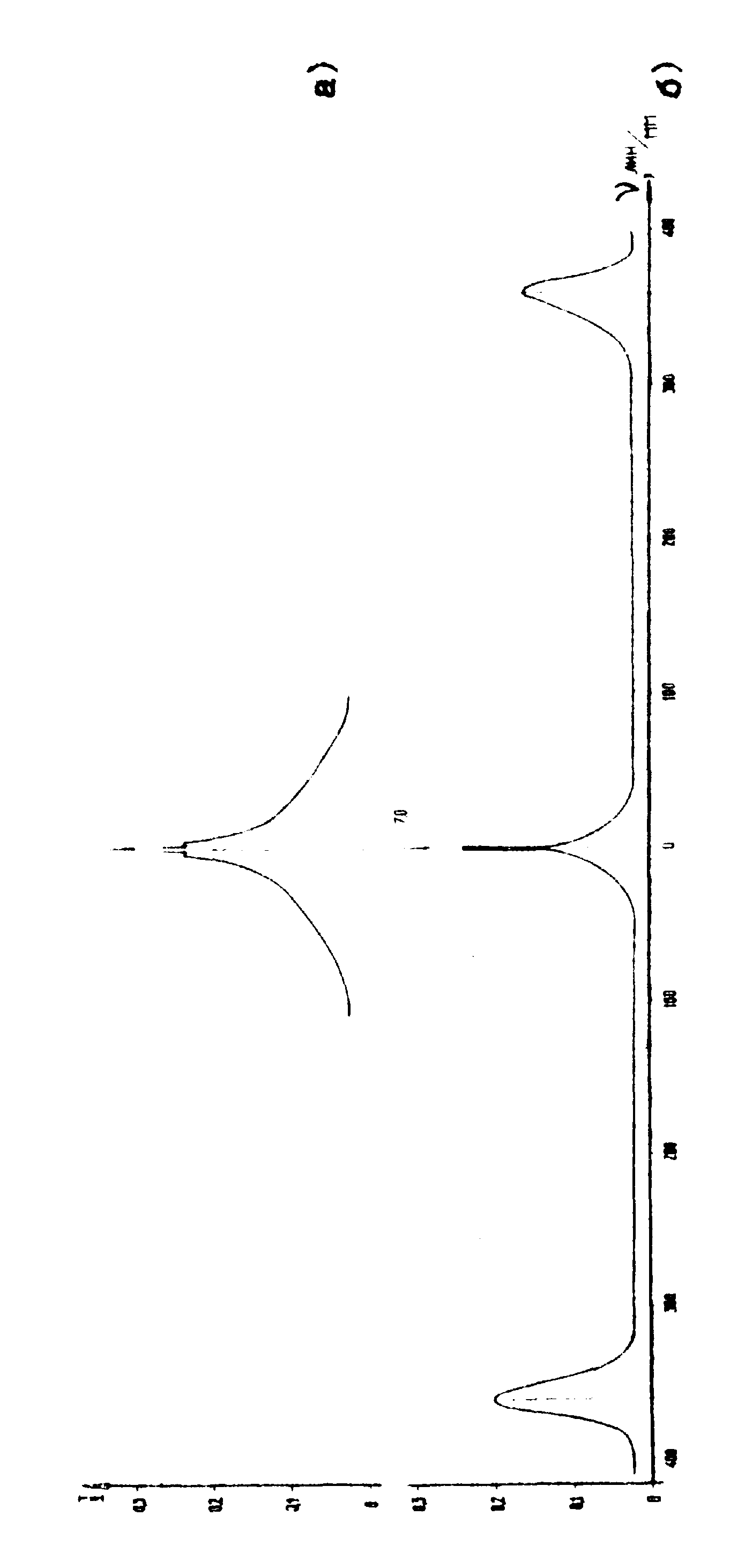
всегда ниже, чем голограммы второго типа (рис.5б). В нашем примере граничные частоты равны ω
1=100 лин/мм и ω2=430 лин/мм.
Понижение верхней границы спектра габоровской голограммы в сравнении с голограммой Лейта и Упатниекса объясняется отсутствием пространственной несущей в габоровских голограммах. Для оспектра, приведённого на рис.5б, несущая ω
0=390 лин/мм. По виду спектра, можно отличать габорокские голограммы от голограмм Лейта-Упатниекса, так как спектр последних характеризуется двумя боковыми распрпределениями пространственных частот, соответствующих мнимому и действительному изображениям /9/.
3.
Восстановление голограмм
Голограммы, полученные по оптическим схемам 1а, 1б, 1в, позволяют восстановить как мнимое, так и действительное изображение /5,6/. Рассмотрим три возможных метода восстановления габоровских голограмм.
a. На рис.6а показан метод косого восстановления. Для рассматривания мнимого или действительного изображния наблюдатеяь должен выйти из зоны, ограниченной крайними лучами восстанавливающего пучка. Этот метод предпочтительнее для восстановления мнимого изображения. Фоновые члены уравнения (1) не снижают качества восстановленного изображения, так как представляют собой плоские волны, распространяющиеся в пределах апертуры восстанавливающего пучка, а лучи, образующие мнимое и действительное изображения, распространяются как внутри, так и вне его. Лучи, вышедшие из зоны восстанавливающего пучка, обусловлены индикатрисой матового рассеивателя, записанной на голограмме, и когерентным рассеянием света на самом объективе. Недостатком этого метода можно считать отсутствие центрального восстановления и исключение из процесса восстановления ближних порядков дифракции, которые фиксируются на голограмме при записи.
Б. Второй метод восстановления служит для наблюдения действительного изображения и представлен ла рис.6б. Действительное изображение восстанавливается за экраном (типа ножа Фуко). Волны,
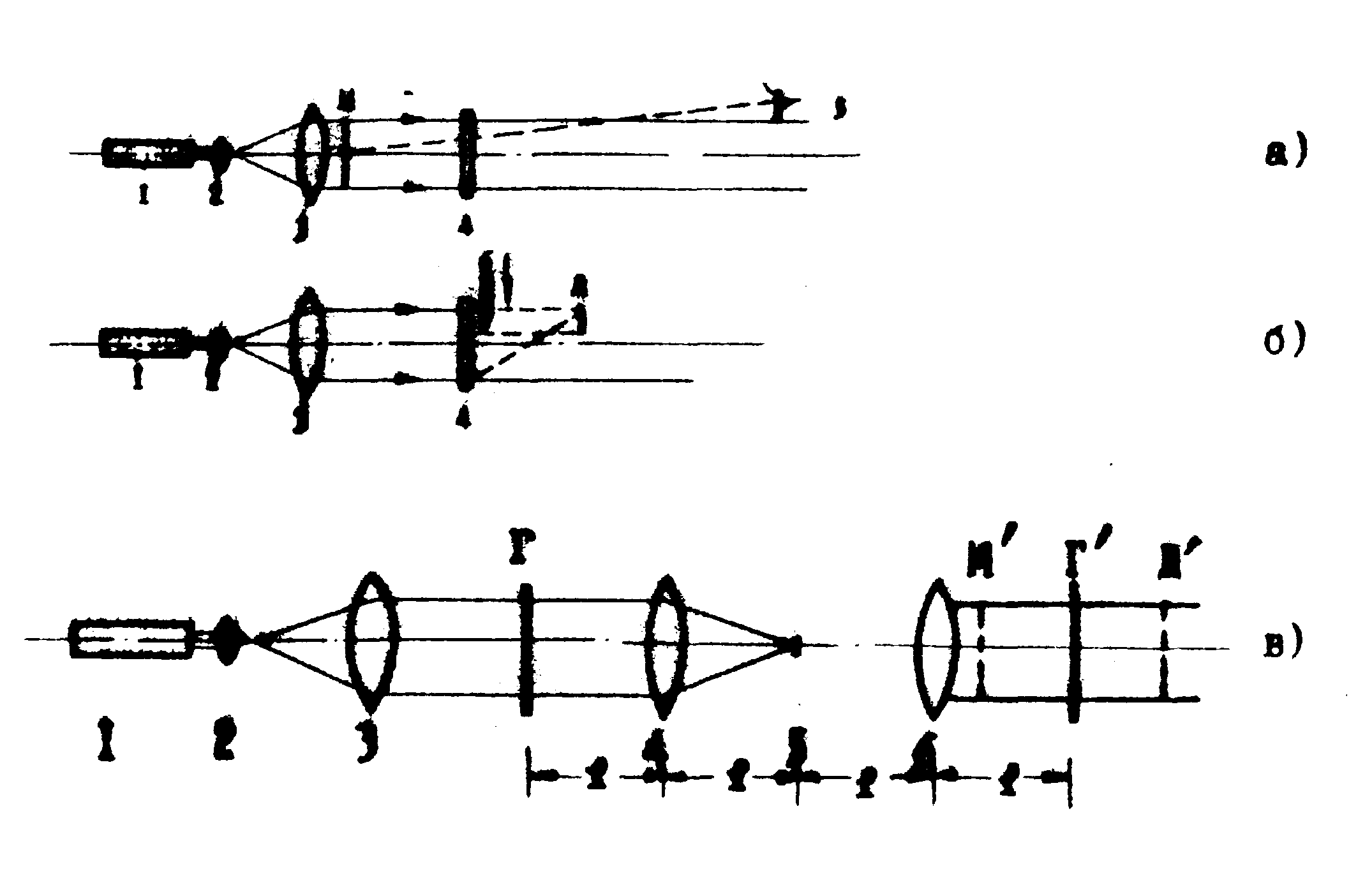
Рис.6. Оптические схемы восстановления голограмм:
а - восстановление мнимого изображения;
б - восстановление действительного изображения.
1 - лазер, 2,3 - коллиммрующие линзы, 4 - голограмма, 5 - наблюдатель, 6 - экран, М и Д - положение мнимого м действительного изображений;
в - восстановление голограммы с помощью фильтра:
1-3 - прежние, 4,6 - линзы с фокусным расстоянием
f , 5 - Фильтр, Г и Г' - голограмма и её изображение, М' и Д'- репроецированные мнимое и действительное изображения.
соответствующие фоновый членам и мнимому изображению (см. уравнение (1)), устраняются экраном. При этом из процесса восстановления выпадает часть голограммы и восстановленное изображение строится аналогично френелевским голограммам типа Лейта-Упатниекса.
Было произведено восстановление значка, голограмма которого выполнена по схеме 1в. Справа от изображения проецируется сечение восстанавливающего пучка. Экран при этом брался в виде круглого отверстия. Этот метод восстановления габоровской голограммы применим в том случае, когда информация о каждой точке объекта записывается на всей голограмме, что приводит к требованию высокой пространственной когерентности записывающего источника. Аналогичный способ восстановления применён Строуком при получении изображения от габоровских фокусированных голограмм /7/. Такое восстановление желательно применять при восстановлении габоровских голограмм мелких объектов, когда линейная апертура голограммы больше размера исследуемого объекта (типа пузырьков, тумана, аэрозолей и т.п.),
так как при этом можно использовать небольшой экран, который незначительно уменьшает светосилу голограммы. Недостатком этого метода является значительное уменьшение действующей апертуры голограммы при восстановленни всей сцены, записанной на голограмме.
В. Третьим методом восстановления может служить использование бинарного или амплитудного фильтра, помещённого в области пространственных частот голограммы. Оптическая схема для такой операции приведена на рис.6в.
Для восстановления голограмма Г освещается коллимированным когерентным светом и устанавливается в передней фокальной плоскости линзы 4. В задней фокальной плоскости образуется спектр пространствемных частот голограммы (см. §2). Так как фоновые члены уравнения (1) соответствуют плоским волнам, они
фокусируются по оси оптической системы, давая резкий пик в области нулевых пространственных частот. Поэтому их влияние можно устранить постановкой бинарного фильтра 5 в виде непрозрачного экрана. Размер фильтра определяется шириной центрального пика в спектре голограммы (рис.4)
и в нашем случае занимает в частотной плоскости ~20 лин/мм. Кроме указанных причин, ширина пика зависит от когерентности источника света и увеличивается с ухудшением когерентности.
Для устранения дифракционных эффектов, обусловленных резким краем фильтра, предпочтительнее использовать амплитудной фильтр. Первым приближением может служить гауссовский фильтр.
Фильтр устанавливается в передней фокальной плоскости линзы 6, репроецирующей изображение голограммы
Г', слева и справа от которой образуется мнимое и действительное изображения исходного пред мета. Оба изображения можно рассматривать визуально, либо на матовом экране. Спектр габоровской голограммы с отфильтрованной центральной частью показан на рис.7.

Рис.7. Спектр габоровской голограммы
с отфильтрованной центральной частью.
Заметим, что приведённая схема восстановления аналогична схеме, используемой для пространственной фильтрации изображения /8/.
Для разделения мнимого и действительного изображения необходимо, чтобы расстояние между изображениями превосходило глубину резкости голограммы Т, определяемую выражением /l0/,
t=2kλp
2/d
2 (5)
где
k- коэффициент порядка единицы, определяемый формой голограммы, λ- длина волны света, р - расстояние между объектом и голограммой, Д- линейная апертура голограммы.
Приведенное значение справедливо для плоских вспомогательных волн, т.е. для габоровских голограмм Фрекеля. В случае габоровских голограмм Фурье мнимое и действительное изображения стропятся в одной плоскости. В этой же плоскости строится изображение источника. И в этом случае разделение изображений не представляется возможным. В промежуточных случаях необходимо при восстановлении учитывать конкретную геометрию голограммы. Примером неудачного использования габоровской схемы голографирования может служдить схема получения голограмм с использованием сферической вспомогательной волны, приведенная в работе /11/, где часть голографируемого объёма, соответствующео мнимому изображению вспомогательного источника, выпадает в силу невозможности разделения мнимого и действительного изображений источника для указанной области
.
З а к л ю ч е н и е
Рассмотренные оптические схемы (рис.1а,б,в) позволяют получать габоровские голограммы объектов любого типа при использовании диффузного освещения. От таких голограмм могут быть восстановлены как мнимые, так и действительные изображения.
Верхняя граница спектра пространственных частот габоровских голограмм много ниже, чем для голограмм с наклонным опорным пучком типа Лейта-Упатниекса с аналогичной угловой апертурой, так как габоровская голограмма не содержит паразитной пространственной несущей, обусловленной интерференцией наклонного вспомогательного и объектного пучков. Понижение верхней границы спектра пространственных частот голограммы позволяет снизить требование к разрешающей способности фотоматериала голограммы и уменьшить хроматическую аберрацию при восстановлении голограмм в коллимированных пучках света широкого спектрального состава
.
Габоровские схемы голографирования позволяют снизить требования к временной когерентности источника, так как максимальная разность хода пучков на голограмме
~d2/4p при d<p, где d -линейная апертура, а р - минимальное расстояние от голограммы до объекта.
Оптическая схема восстановления габоровской голограммы с использованием амплитудного фильтра может быть значительно упрощена помещением голограммы в сходящийся пучок когерентного света и расположением фильтра в фокусе пучка. Однако при этом искажается масштаб восстановленного изображения. Этот метод применяется при восстановлении звуковых голограмм.
Габоровские схемы могут быть использованы при изготовлении комплексных фильтров. При использовании таких фильтров для обработки изображений оптические элементы анализатора располагаются в линию, но при этом необходимо вводить дополнительно бинарный либо амплитудный фильтр для подавления некогерентного фона, обусловленного первыми двумя членами выражения (1).
Л и т е р а т у р а
1. d.gabor. proc.roy.soc., a 197. 454 (1949).
2. И.С.Клименко, Г.И.Рукман. Оптика и спектроскопия,
21, 751 (1966).
3. g.w.stroke et al., brit.j.appl.phys., 17, 497 (1966).
4. А.П.Комар, М.В.Стабников, Б.Г.Турухано. ДАН,
173, 1059 (1967).
5. Б.Г.Турухано, Н.Турухано. Использование О К Г в современной технике. ЛДНТП, Л.,
1, 75 (1969).
6. А.П.Комар, Б.Г.Турухано, Н.Турухано. ДАН,
186, 1312 (1969).
7. g.w.stroke. phys.letters, 23, 325 (1966).
8. a.v.lught., 0ptica acta, 15, 1 (1968).
9. e.leith, j.upatnieks. josa, 52, 1123 (1962).
10. Б.Г.Турухано. Ж Т Ф,
40, 181 (1970).

