|
|
 |
 |

|
| |
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ГОЛОГРАФИИ,
использующей ТРЁХМЕРНЫЕ РЕГИСТРИРУЩИЕ СРЕДЫ
В.В.Аристов
Трёхмерные голограммы представляют собой пример физического прибора, который позволяет регистрировать информацию и трёхмерной среде. Считывание этой информации производится дифракцией, реконструирующей волны на голограмме. Как при записи, так и при считывании происходит кодирование и потеря информации. Поскольку считывание может быть проведено в принципе и без дифракции, рассмотрим вначале, какая информация о волне может быть зарегистрирована на трёхмерной голограмме. Затем каснёмся вопроса о том, к каким явлениям приводит реконструкция изображения при дифракции на голограмме реконструирующей волны.
1. Регистрация или измерение волны света при записи трехмерной голограммы
Будем полагать, что голограмма находится на таком расстоянии ro от объекта, что можно считать его много большим размеров голограммы и предмета. Поэтому поле, регистрируемое голограммой, представляет собой Фурье-спектр пространственных частот волны на поверхности предмета. Так, например, если предмет состоял из n когерентно светящихся точек, то при квадратичное детектировании голограмма будет состоять из (n2-n)/2 элементарных гармонических распределений показателя преломления, а её Фурье-спектр - из n2-n точек (узлов), не лежащих в начале координат Фурье-пространства. Несмотря на то, что Фурье-спектр голограммы соответствует автокорреляции функции, описывающей волну на предмете, оказывается возможным выделить ту часть спектра, которая соответствует самой функции. Это можно понять из следующих рассуждении.
Пусть происходит квадратичная регистрация с помощью плоского детектора n когерентных
плоских волн с вопновыми векторами 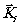 .
Для их определения после детектирования мы получим следующие уравнения: .
Для их определения после детектирования мы получим следующие уравнения:
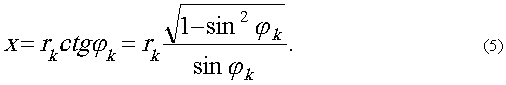
где i,j принимают
значения 1,2... n при i = j, 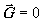 .
Всего независимых уравнений 2(n-1),
в то время как неизвестных -3n.
Поэтому принципиально невозможно определить значения .
Всего независимых уравнений 2(n-1),
в то время как неизвестных -3n.
Поэтому принципиально невозможно определить значения 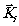 .
При регистрации а объёме мы получим дополнительно уравнения: .
При регистрации а объёме мы получим дополнительно уравнения:
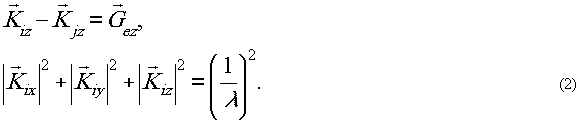
Добавилась ещё n-1=n уравнений и одно неизвестное λ. Число неизвестных равно теперь n > 4 и меньше числа уравнений при n>4. Поэтому можно определить как волновые вектора, так и частоту всех плоских волн, что не удаётся сделать при обычном квадратичном детектировании на поверхности.
Заметим, что плоская голограмма позволяет выделить изображение предмета только при наличии априорных сведений об относительном расположений опорной волны и голограммы, тогда как детектирование трёхмерного распределения энергии волны света позволяет взаимно однозначно описать распределение амплитуд и, с точностью до постоянной, фаз этой волны.
Рассмотрим теперь вопрос о том, с какой точностью регистрируется волна в ограниченном объёме голограммы. Пусть для простоты голограмма имеет форму прямоугольного параллелепипеда размерами xyz. В Фурье пространстве голограммы каждый узел имеет в этом случае конечные размеры: 1/x, 1/y, 1/z. Компоненты волнового вектоhа любой волны могут быть найдены в общем случае с точностью,
определяемой этими размерами. Выражение для распределения интер-ференционной
функции в Фурье-пространстве ограниченной голограммы вокруг определённого узла,
определяемого вектором 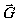 задаётся формулой
задаётся формулой
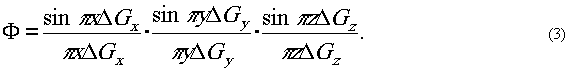
Первые два сомножителя задают размер изображения точки, получаемой с помощью идеальной плоской голограммы.
В предыдущем изложении предполагалось, что нам неизвестна геометрия получения
трёхмерной голограммы. В этом случае удаётся найти положения волновых векторов
с точностью, определяемой формулой (3). Для плоской голограммы неопределённость
по 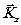 устраняется, если известна геометрия получения голограммы; неопределённость
аае по остальным компонентам
устраняется, если известна геометрия получения голограммы; неопределённость
аае по остальным компонентам 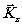 , ,
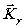 вычисляатся по формуле (3). Интересно остановиться на том важном случае, когда
геометрия известна и при получении трёхмерной голограммы; Поскольку теперь мы
имеем определённую сферу Эвальда в Фурье-пространстве голограммы, то нас интересуют
лишь те части узлов, которые попадают на сферу, заданную геометрией записи голограммы.
В этом случае
вычисляатся по формуле (3). Интересно остановиться на том важном случае, когда
геометрия известна и при получении трёхмерной голограммы; Поскольку теперь мы
имеем определённую сферу Эвальда в Фурье-пространстве голограммы, то нас интересуют
лишь те части узлов, которые попадают на сферу, заданную геометрией записи голограммы.
В этом случае 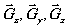 связаны между собой уравнением сферы
связаны между собой уравнением сферы
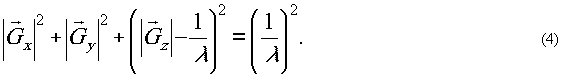
Это условие связывает между собой 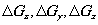 и, следовательно,
и, следовательно, 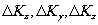 для любого вектора
для любого вектора 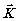 -волны,
реконструируемой с голограммой. Легко показать, что -волны,
реконструируемой с голограммой. Легко показать, что
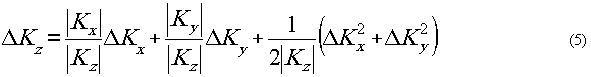
Из (5) и (3) следует, что функция Ф(Δ kx, Δky, Δkz) для трёхмерной голограммы, чем для плоской, а при
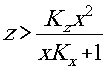
нули этой функции лежат ближе к максимуму, чем для плоской голограммы.
На рис.1 изображена схема модельного эксперимента, который позволяет установить
влияние толщины голограммы на разрешение /1/. При реконструкции голограммы перед
ней помещалась щель шириной 200μ
, так что размер голограммы в направлении х был равен 200
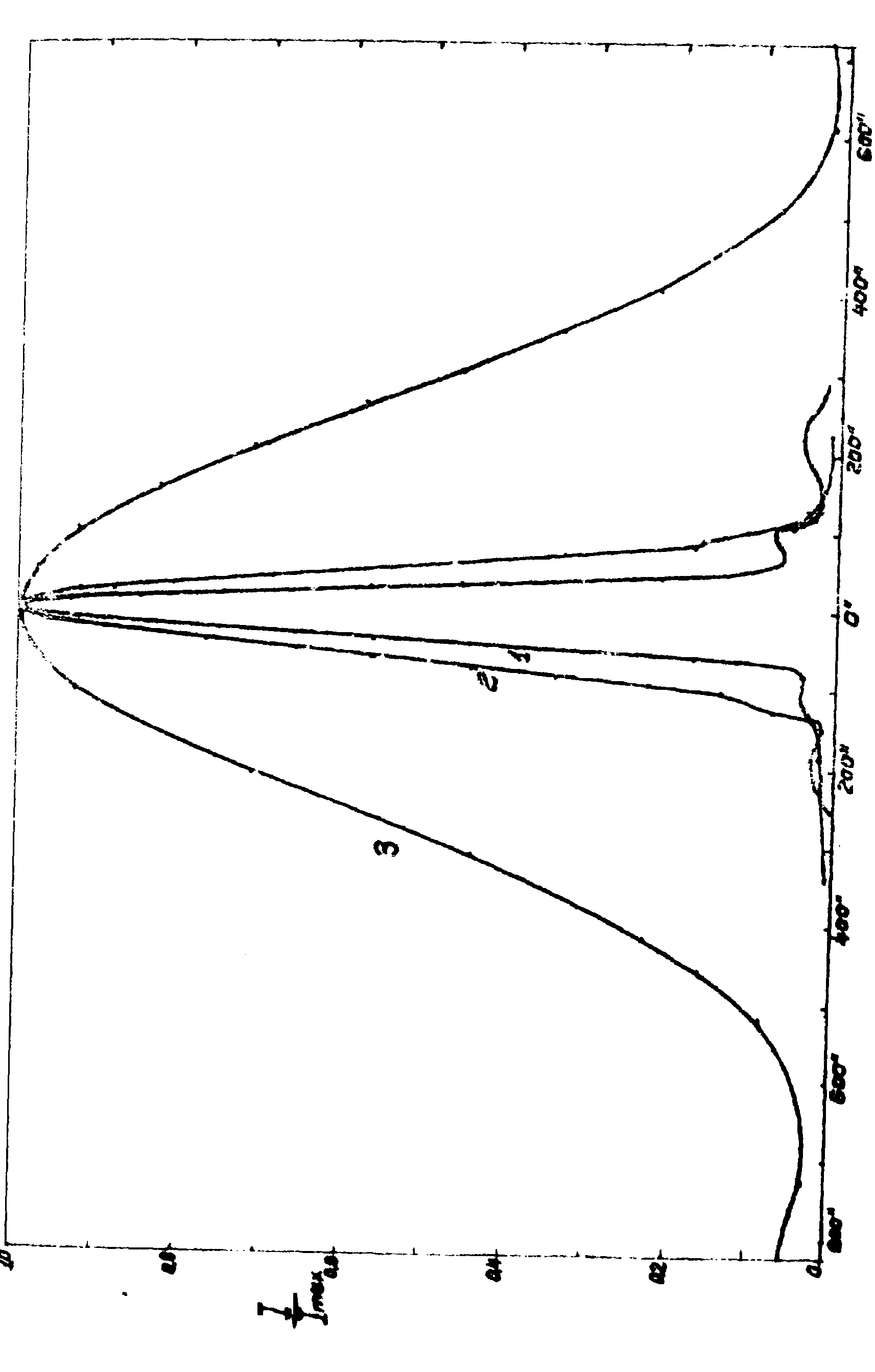
μ. На рис.2 приведены экспериментальные
кривые, полученные при измерении распределения 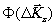 на голограмме толщиной
на голограмме толщиной z = 6
мм и z
= 12 мм.
Минимумы приведённых экспериментальных кривых совпадают с теми, вторые могут
быть вычислены из (3)
с учётом (5).
Таким образом, трёхмерная голограмма позволяет получать лучшее разрешение в изображении точек предмета, чем то, которое получается при реконструкции с плоских голограмм. Особенно это замечание относится к точкам, не лежащим на оптической оси. Легко показать, что трёхмерная голограмма даёт лучшее разрешение и по направлению z. Поэтому трёхмерные голограммы желательно использовать для передачи изображения как плоских, так и трёхмерных предметов.
Используя полученный результат, оценим предельную информационную ёмкость, которая может быть записана в трёхмерной голограмме. Объём, занимаемый узлом в Фурье-пространстве голсграммы, v*=1/v, где v- объём голограммы. Объём Фурье-пространства,
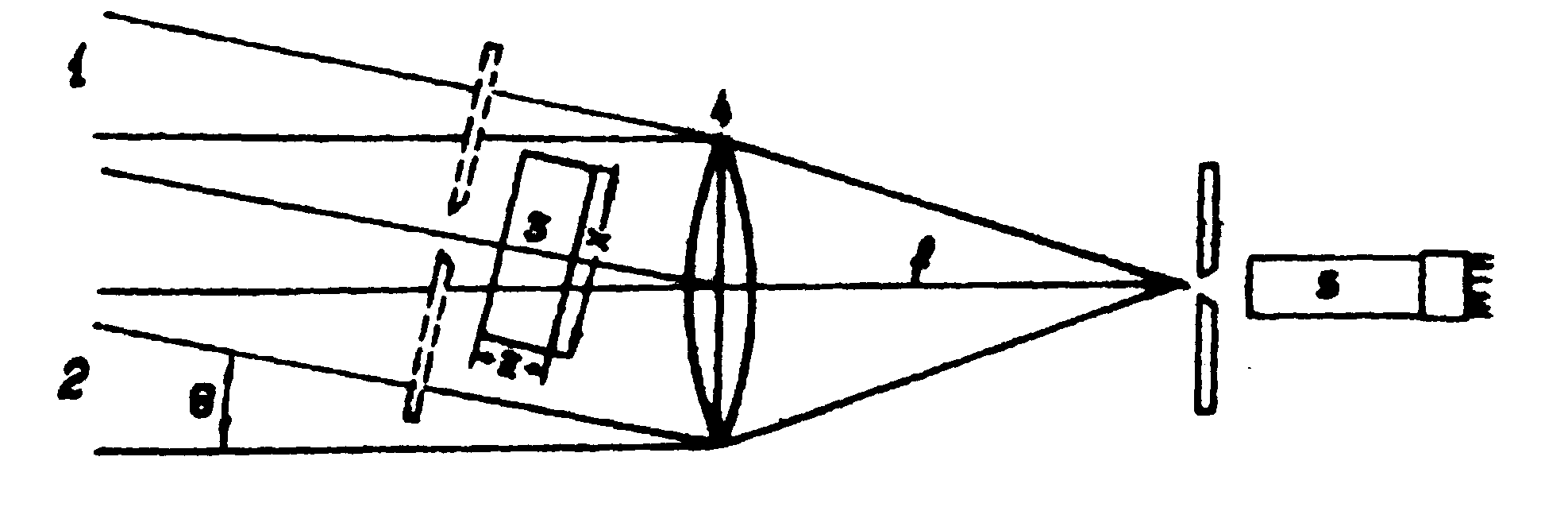
Рис.1 . Схема эксперимента для измерения распределения интенсивности в восстановленной из голограммы 3 плоской волны 2.
Пунктиром отмечена щель, которая помещаась перед голограммой при реконструкции. Угол Θ равен 11,30. 4 - линза, 5 - ФЭУ.
точки которого могут попадать на сферу Эвальда, равен 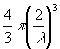 (рис.3). Поэтому в Фурье-пространстве голограммы можно поместить
(рис.3). Поэтому в Фурье-пространстве голограммы можно поместить 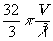 независимых элементов nmax.
Если голограмма записывалась от n точек, то n = n2
- n и
независимых элементов nmax.
Если голограмма записывалась от n точек, то n = n2
- n и 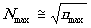 .
При записи голограммы с выделенным по яркости опорным пучком, когда можно пренебречь
всеми узлами, кроме тех, которые вызваны интерференцией между опорным пучком
и остальными волнами, .
При записи голограммы с выделенным по яркости опорным пучком, когда можно пренебречь
всеми узлами, кроме тех, которые вызваны интерференцией между опорным пучком
и остальными волнами, 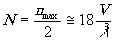 (сравни /2/). Отношение мощности сигнала к мощности шума не больше отношения
энергии, содержащейся в центральном максимуме, к энергии, содержащейся во всех
остальных порядках дифракции. Максимальное количество информации, записываемое,например,
в голограмме объёмом 1 см3
волной λ = 1μ , οоряцка
1013
бит.
(сравни /2/). Отношение мощности сигнала к мощности шума не больше отношения
энергии, содержащейся в центральном максимуме, к энергии, содержащейся во всех
остальных порядках дифракции. Максимальное количество информации, записываемое,например,
в голограмме объёмом 1 см3
волной λ = 1μ , οоряцка
1013
бит.
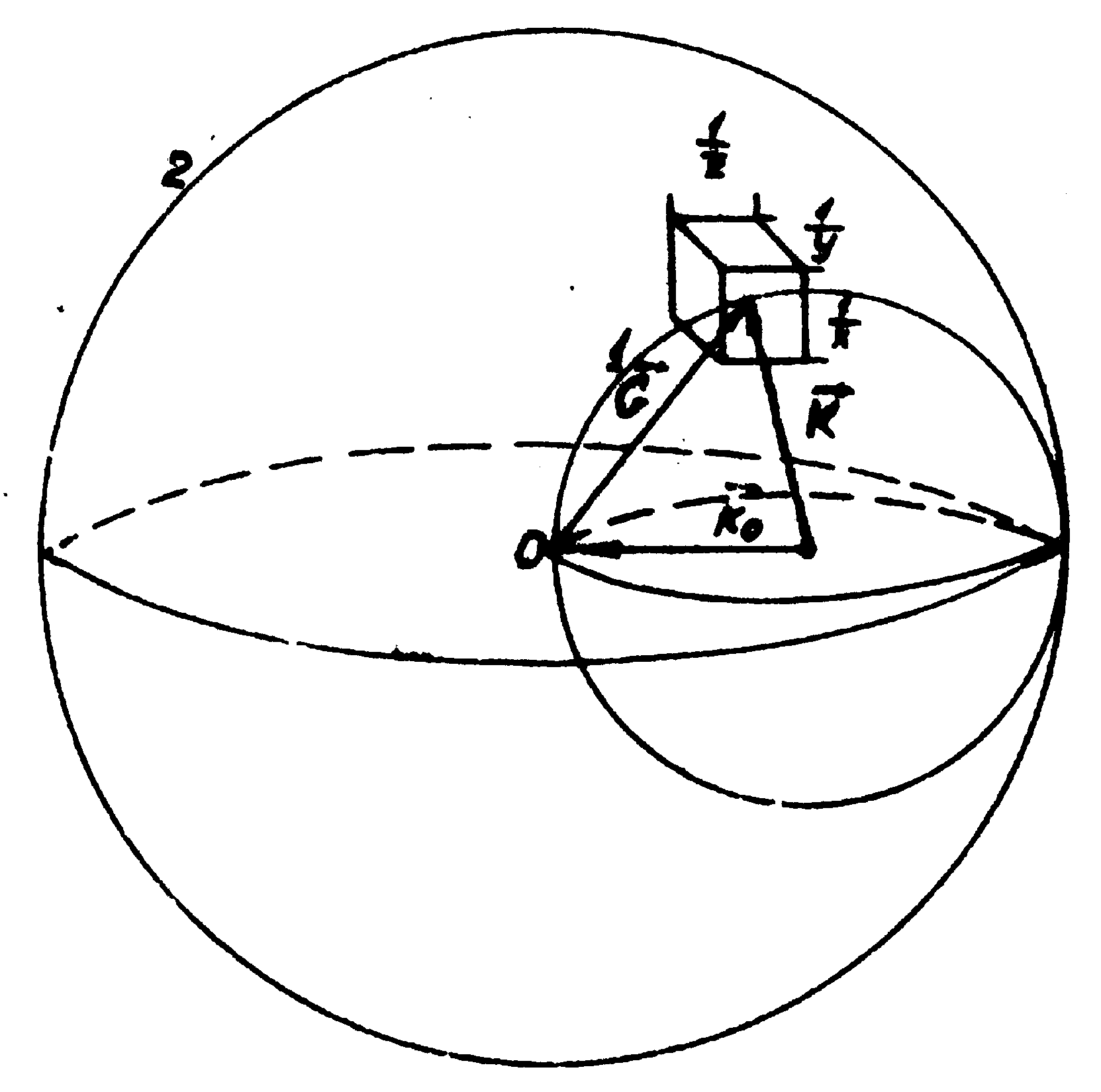
Рис.3. Объём Фурье-пространства, "доступный" для волны с длиной λ .
Этот объём ограничен сферой 2.
Радиус сферы ограничения 2/ λ. Внутри неё лежат
все сферы Эвальда, которые могут быть построены для любых направлений волнового
вектора 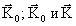 соответствуют двум произвольным волнам, принимавшим участие в записи голограммы.
соответствуют двум произвольным волнам, принимавшим участие в записи голограммы.
В заключении первой части лекции найдём спектральную разрешающую силу трёхмерных голограмм. Мы видели, что угловая ширина изображения зависит от толщины z. Предположим для определённости, что x = У = z. В этом случае угловая полуширина дифракционного максимума приблизительно постоянна для любого направления дифракции и равна λ/2x. Из условия Вульфа-Брегга найдём, что Δλ=2d cos φΔφ. Εсли определить разрешающую силу r так яв, как это делается в оптике для плоских дифракционных решёток*, то, если n=x/d,
r = n/cosφ. (6)
Здесь φ - половина угла между двумя плоскими волнами при записи голограммы. Из (6) видно, что трёхмерная голограмма может дать очень высокую разрешающую силу, большую, чем у плоских дифракционных решёток с числом штрихов n, причём с неменьшей област дисперсии. Такое свойство трёхмерных голограмм делает их перспективными при использовании в качестве дисперсионных приборов.
2. Реконструкция изображения
В первой части лекции мы рассмотрели вопрос записи информации на трёхмерную голограмму. Восстановление изображения происходит в результате дифракции реконструирующей волны на голограмме. Если ограничиться приближением теории трёхмерной дифракции, которое позволяет пользоваться аппаратом Фурье-преобразований, то легко проанализировать различные экспериментальные схемы, которые позволяют записывать и реконструировать изображение предмета так, как это было сделано, например, в лекции В.Ш.Шехтмана. Это приближение обычно используется при описании свойств трёхмерных голограмм /3/. Однако оно требует выполнения следующих
условий: реконструирующая волна не ослабляется при прохождении голограммы, дифрагированные волны не испытывают вторичного рассеяния внутри голограммы. Ясно, что оба предположения приблизительно выполняются лишь при дифракционной эффективности, много меньшей единицы. Посмотрим, к чему может привести отказ от такого приближения.
Пусть голограмма записана от двух светящихся точек. Для реконструирующей волны, посылаемой одной из точек предмета, эта голограмма является резонансной системой. Наиболее просто можно понять некоторые свойства трёхмерных голограмм на механической модели резонансной системы, состоящей, например, из маятников (рис.4.), маятники в этой модели соответствуют реконструирующей и дифрагированной волне, а жёсткость пружины между ними -амплитуде синусоидального распределения показателя преломления голограммы. Известно, что колебания в этой системе носят характер биений. Такие же биения интенсивностей реконструирующего луча и восстановленного изображения должны наблюдаться при реконструкции трёхмерных голограмм с увеличением их толщины. Оценки показывают, что колебания интенсивности будут наблюдаться при толщине z>λ/Δn, где Δn - вариация показателя преломления, обусловленная записью голограммы. Используемые в настоящее время голограммы имеют меньшие толщины.
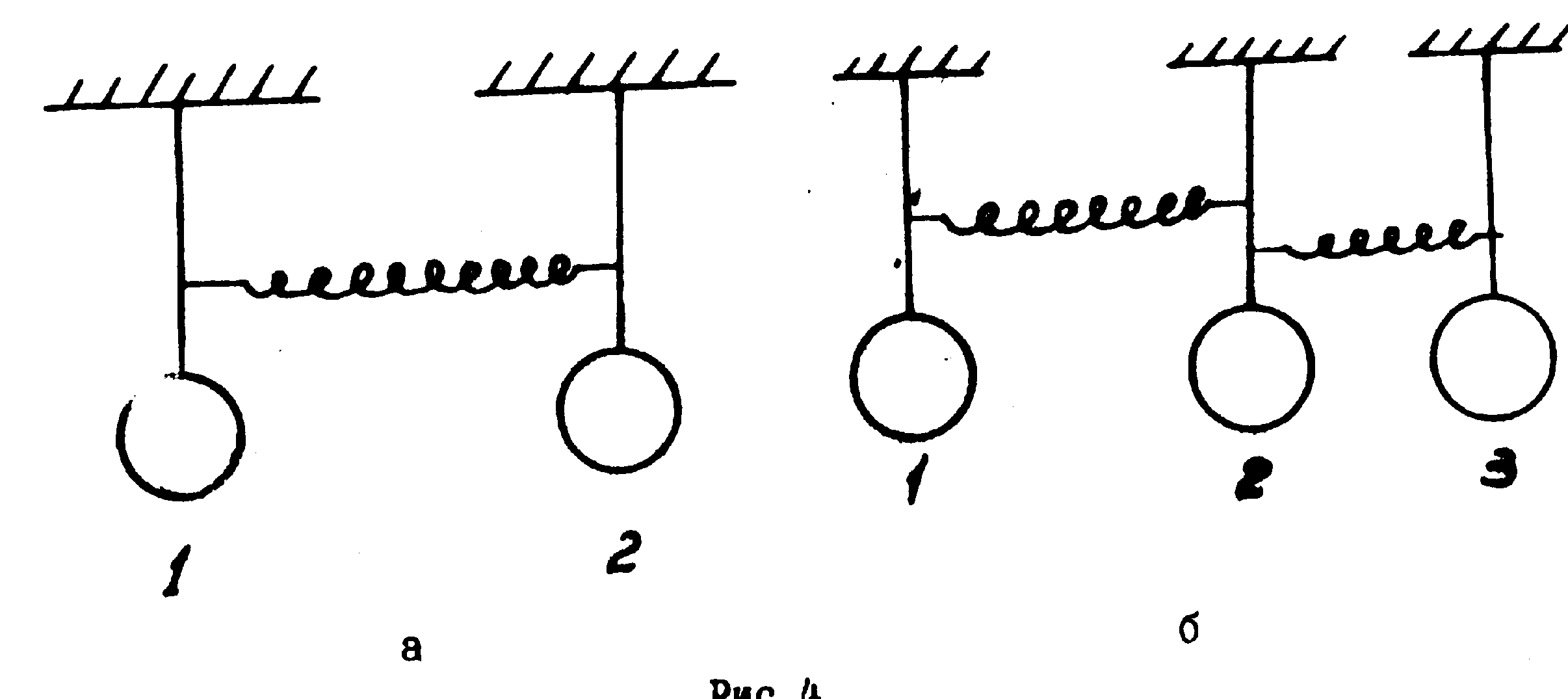
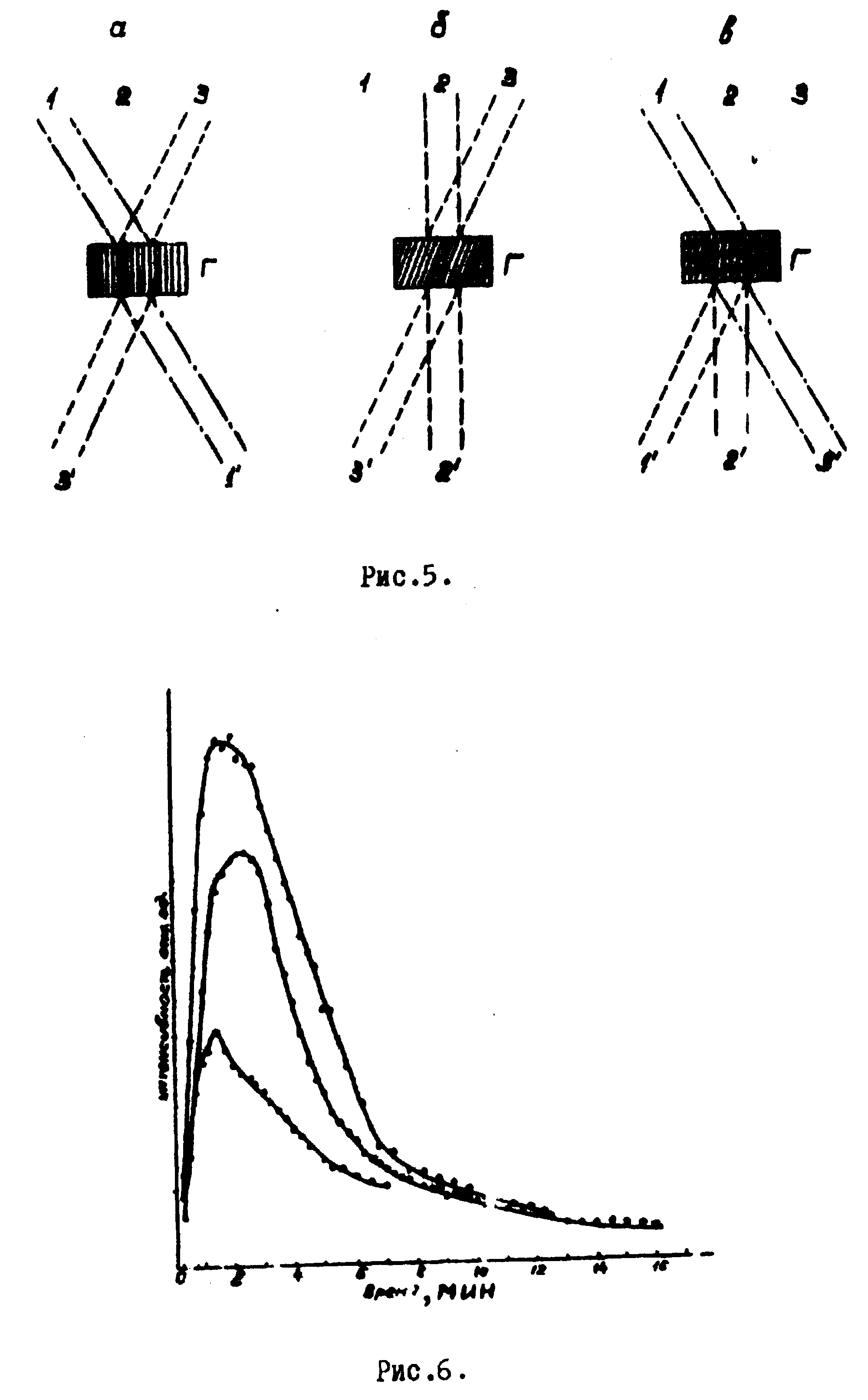
Посмотрим теперь, что произойдёт, если голограмма записывается так, как показано на рис.5. Вначале голограмма записывается воинами 1 и 5 (рис.5а), затем волнами 2 и 3 (рис.5б). Если осветить голограмму волной 1 при реконструкции (рис.5в), то условия Вульфа-Брегга выполнится для одной гармоники и появится дифрагированная волна 3. Для волны 2 условие Вульфа-Брегга не выполняется. На нашей модели маятников подобная резонансная система представлена на рис.4б. Маятники 1 и 3 непосредственно не связаны между собой, однако легко видеть, что если заставить колебаться первый маятник, то будет совершать колебания не только второй, но также и третий маятник.
Аналогично внутри голограммы при реконструкции волной 1 возникает волна 3, которая становится реконструирующей для волны 2. Поэтому наряду с волной 3 в реконструируемом изображении появится и волна 2. На рис.6 показаны результаты измерений интенсивности "лишней'' волны в зависимости от времени второй экспозиции для разных голограмм. Наличие максимумов связано с тем, что голограммы записывались на окрашенных щелочно-галоидных кристаллах К cl. При записи голограммы для волн 2 и 3 происходит общее высвечивание центров окраски и, следовательно, стирание голограммы для волн 1-3. Подобный эффект наблюдается при дифракции рентгеновских лучей и носит название эффекта Ренингера или окольного возбуждения.
Интенсивность "лишней" волны зависит от толщины голограммы, поскольку в такой резонансной системе так же, как и в предыдущем случае, будут происходить биения интенсивностей всех трёх волн. При достаточно малых толщинах z<λ/Δn интенсивность "лишней'' волны будет пропорциональна произведению интенсивности реконструирующей волны на квадрат дифракционной эффективности. При больших толщинах рассмотренный эффект приведёт к появлению "лишних" изображений, интенсивность которых сравнима с интенсивностью основных изображений. Можно сказать, что трёхмерная голограмма обладает ассоциативной памятью, аналогичной лингвистической памяти человека при изучении им иностранного языка. В памяти человека в этом случае имеются связи между представлениями об определенных предметах и словами родного языка, с одной стороны, и,
о другой, между словами родного языка и иностранного. При чтении иностранных слов представления о предметах возникают лишь после перевода на свой язык. Только после длительных упражнений могут появиться прямые связи, представления предметов в словах иностранного языка. Последнее аналогично записи голограмм в фотохромных материалах, когда при реконструкции происходит также запись голограммы для "лишней" волны.
Заметим, что в результате эффекта Ренингера интенсивность реконструированного изображения будет искажаться и не будет равна той, которую можно вычислить, пользуясь аппаратом Фурье-преобразований. Оценим ёмкость памяти трёхмерной голограммы, которая может быть использована при "считывании" информации световой волной. реконструирующей изображение. При большой дифракционной эффективности и достаточной толщине для появления интенсивных лишних изображений число независимых элементов памяти внутри трёхмерной голограммы при Х = У = z будет порядка 4πs/λ2 , где s - площадь поперечного сечения голограммы. Это количество равно тому числу узлов, которое укладывается на одну сферу Эвальда на рис.4. При дифракции световой волны на такой голограмме внутри её возникнут волны, занимающие весь телесный угол, так что благодаря рассмотренному эффекту реконструируются лишние изобраажения, соответствующие любому узлу, не лежащему на сфере Эвальда. Эти "лишние" изображения накладываются на основные. Поэтому можно считать, что указанное выше число независимых элементов памяти является предельным для трёхмерных голограмм и обусловлено характером "считывания" информации*. Предельная ёмкость
памяти трёхмерной голограммы в этом случае не больше 10 10 бит при λ = 1μ, v = 1см3.
До сих пор мы предполагали, что изображение реконструируется с фазовой голограммы. Пусть голограмма имеет отличный от нуля коэффициент поглощения μ 0. При выполнении условия Вульфа-Брегга
коэффициент поглощения для определённого вида колебаний становится меньше μ 0 так же, как в системе двух маятников, погруженных в вязкую среду. Если μ0z>> 1, интенсивность волны, проходящей через голограмму, может стать больше в том случае, когда выполняется условие Вульфа-Брегга.
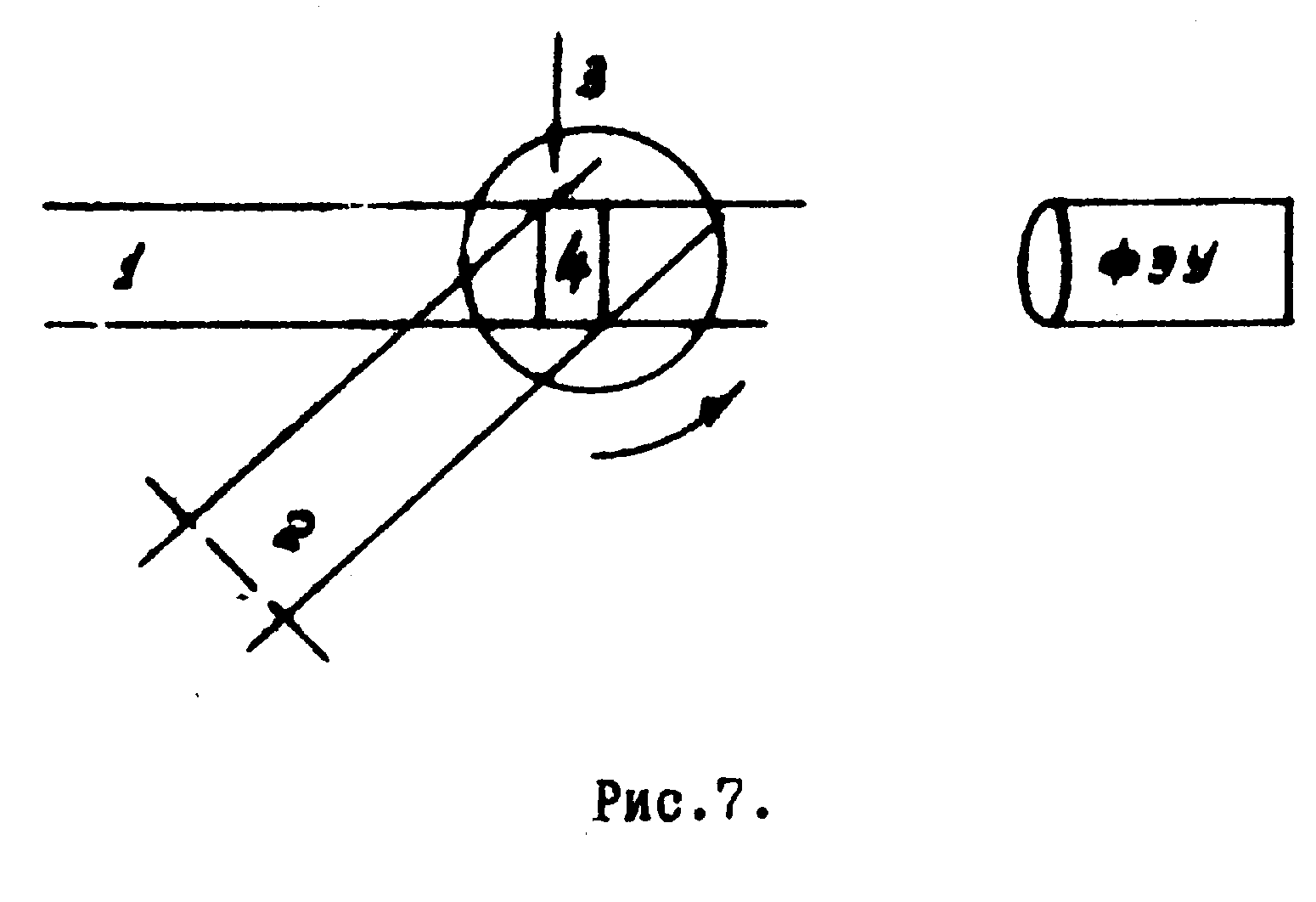
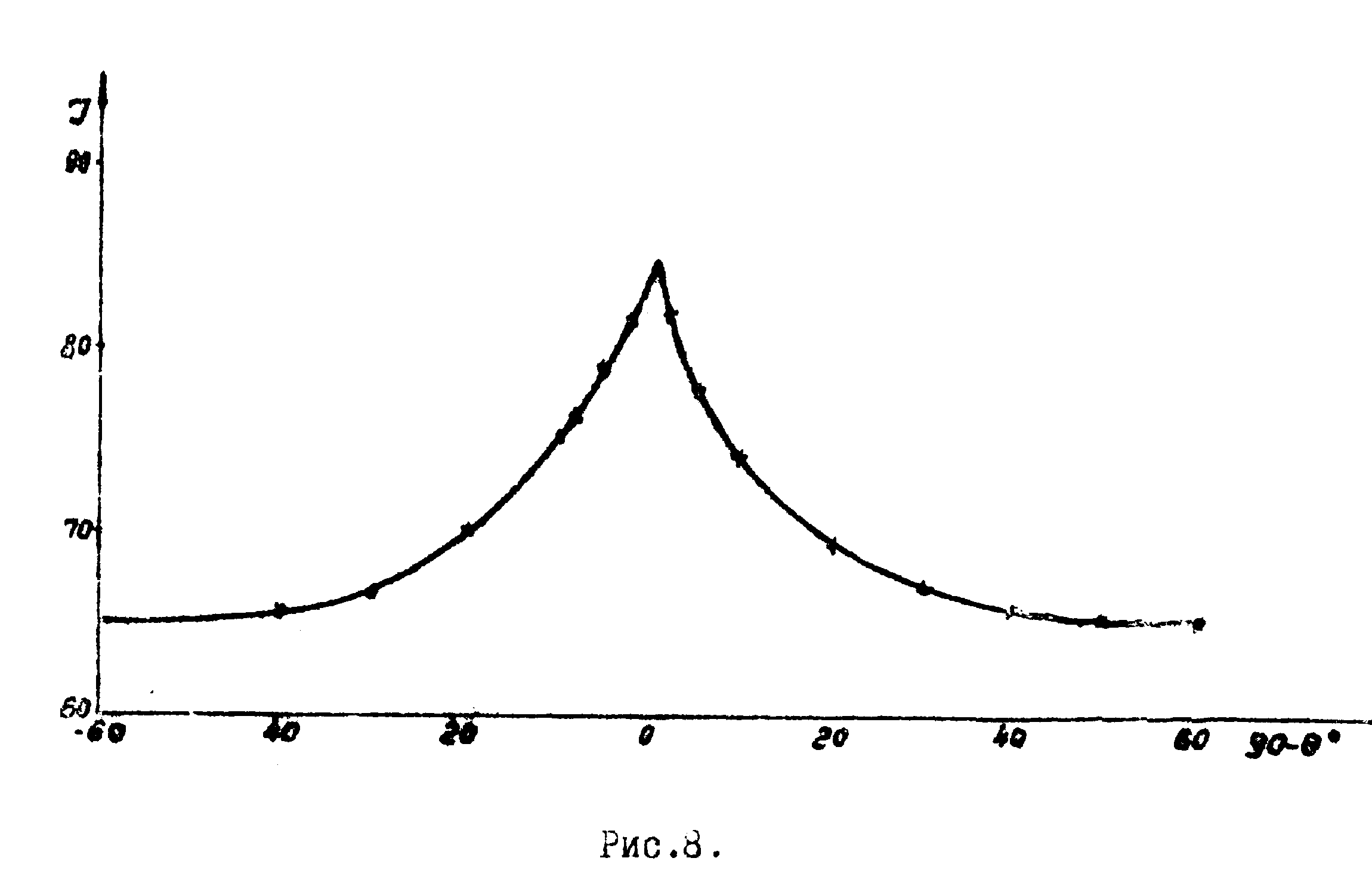
На рис.7 изображена схема эксперимента для обнаружения эффекта аномального прохождения. Голограмма записывается волнами 1 и 2. Затем, закрыв волну 2 и поворачивая голограмму 4, установленную на платформе 5, можно следить за интенсивностью луча 1, проходящего через голограмму. На рис.8 представлена экспериментальная кривая для голограммы толщиной 0,5 см, записанной на окрашенном щелочно-галоидном кристалле k br, облучённом дозой i06 рад. Поскольку всё явление наблюдается в пределах нескольких десятых градуса отклонения от угла Вульфа-Брегга, длина пути проходящего луча приблизительно постоянна. Поэтому изменение интенсивности связано лишь с изменением коэффициента поглощения. Аналогичный эффект впервые наблюдался Боррманном при изучении дифракции, рентгеновоких лучей на совершенных кристаллах.
Мы рассмотрели некоторые простейшие следствия, которые вытекают иэ более строгого решения задачи реконструкции изобраюния ив трёхмерной голограммы.
В заключение отметим, что развитие теории трёхмерных голограмм позволит более глубоко понять явления трёхмерной дифракции, основы которой рассмотрены в теории дифракции рентгеновских лучей, электронов и нейтронов на совершенных кристаллах, поскольку голографическим методом можно получить как различные трёхмерные дифракционные структуры, моделирующие кристаллические структуры, так и структуры более общего вида.
В настоящее время практическое использование трёхмерных голограмм тормозится отсутствием трёхмерных сред для регистрации интерференционной картины. Однако можно ожидать, что в ближайшие годы трёхмерные голограммы найдут не менее широкое применение, чем плоские.
Л и т е р а т у р а
1. В.В.Аристов, В.Г.Лысенко, В.Б.Тимофеев, В.Ш.Шехтман. ДАН, 191, 4, 797 (1970).
2.p.v. van heerden. Зарубежная радиоэлектроника, № 2, 32 (1964).
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

