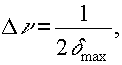СТРУКТУРА ИНТЕРФЕРЕНЦИОННЫХ ПОЛОС
П.Ф. Паршин
В своем выступлении я хочу рассмотреть в общих чертах структуру интерференционных полос, возникающих в двухлучевых интерферометрах, обратив внимание на место и характер локализации этих полос, а также на связь угловых разеров источника с контрастностью полос. Очевидно, что все эти вопросы преставляют несомненный интерес но только для интерферометрии в классическом её применении, но также и в голографии при анализе структуры и качества голограмм.
Остановимся на общих закономерностях при наблюдении интерференционных картин в разных типах двухлучевых интерферометров. Тяковыми являются:
1) для монохроматического света - возникновекие в изображении периодической структуры ( в случае полихроматического излучения для светоделителей типа муаровой решётки Ронки наблюдаем ахроматическую структуру);
2) падение контрастности за счёт пространственных и спектральных свойств источника;
3) связь между угловыми размерами источника и числом полос.
Остановимся на первом из перечисленных свойств. В случае двухлучевой интерференции основными формами полос будут полосы равной толщины и полосы равного наклона (рис.1). Если световой поток, исходящий из источника s , падает под углом θ к поверхности полупрозрачной пластины, то, разделяясь последней на два пучка, может быть собран линзой Λ в точку Р, где мы и наблюдаем интерференционную картину. В этом случае реализуются полосы равного наклона, локализованные в бесконечности. Полосы равной толщины реализуются схемой, изображённой на рис.2. Поток от источника s , попадая на клин К , разделяется последним и собирается в точку Р . В данном случае полосы локализуются вблизи поверхности клина.
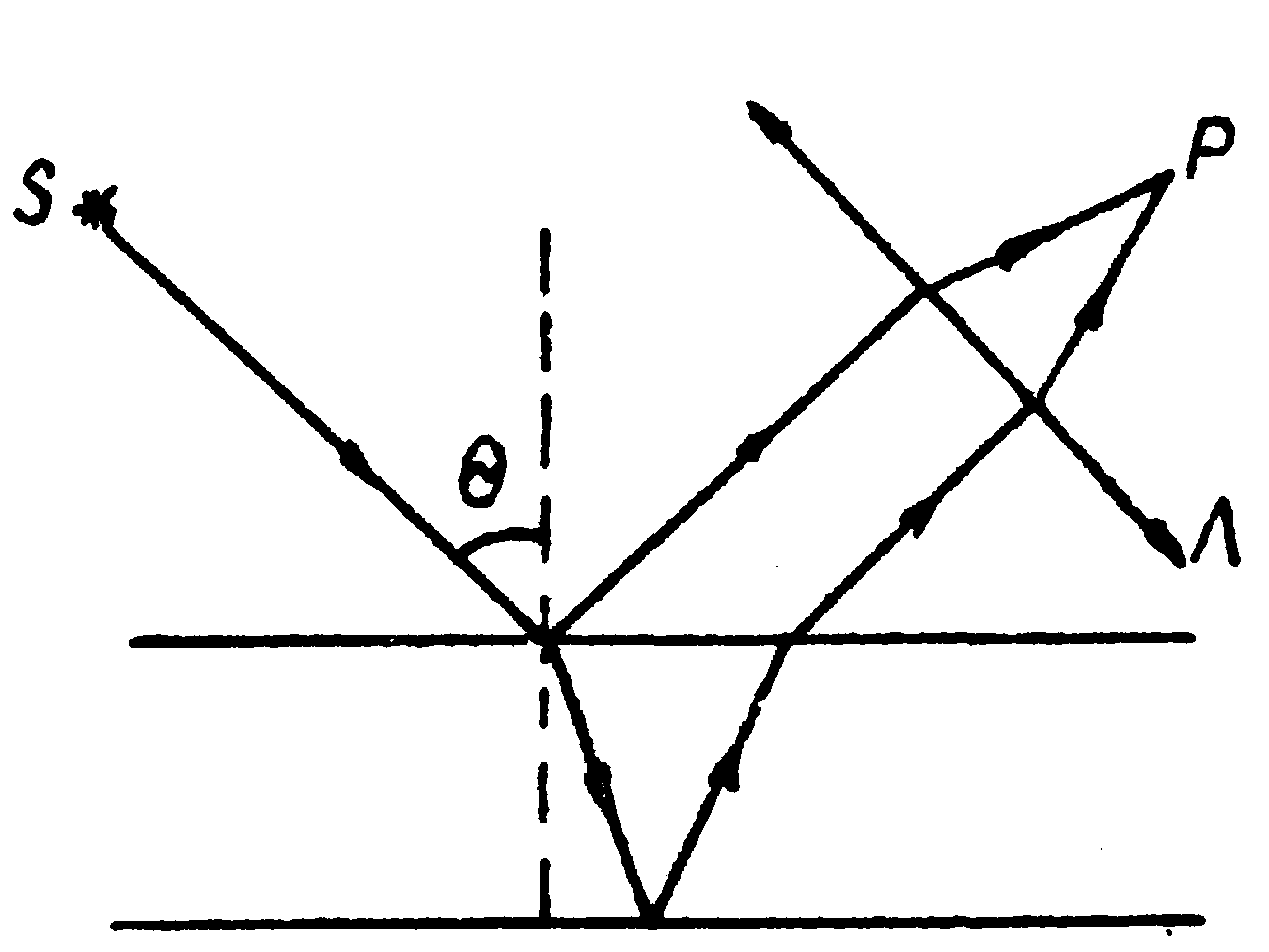
Рис.1. Полосы равного наклона:
s- источник; Λ- λинза; Р- точка, в которой наблюдается интерференционная картина; θ - угол падения.
Возникновение полос двух типов в интерферометре Майкельсона (рис.3) объясняется тем, что полосы Физо или полосы равной толщины локализуются до линзы вблизи зеркала М1, а полосы Хайдингера или полосы равного наклона возникают в фокусе линзы в виде концентрических окружностей.
Вычислим период полос равной толщины. Для этого обратимся к рис.3. Источник s расположен в фокусе линзы, а поэтому на светоделитель n попадает параллельный пучок лучей. Зеркала М1 и М2 в интерферометре Майкельсона расположены таким образом, что плоскость зеркала М1, перпендикулярна направлению распространения отражённых от светоделителя лучей, а плоскость зеркала m2 составляет малый угол α с этим же нaпpaв^eниeм (рис.4).
Разность хода δ μежду лучами прямым и отражённым от светоделителя определяется как δ = δ1 - δ2 (мы исходим из того, что δ = 0 для центрального луча - луча, приходящего в О). В виду малости α имеем:
α~ sinα~ tgα и δ~ 2xsinα,
где x определён на рис.4.
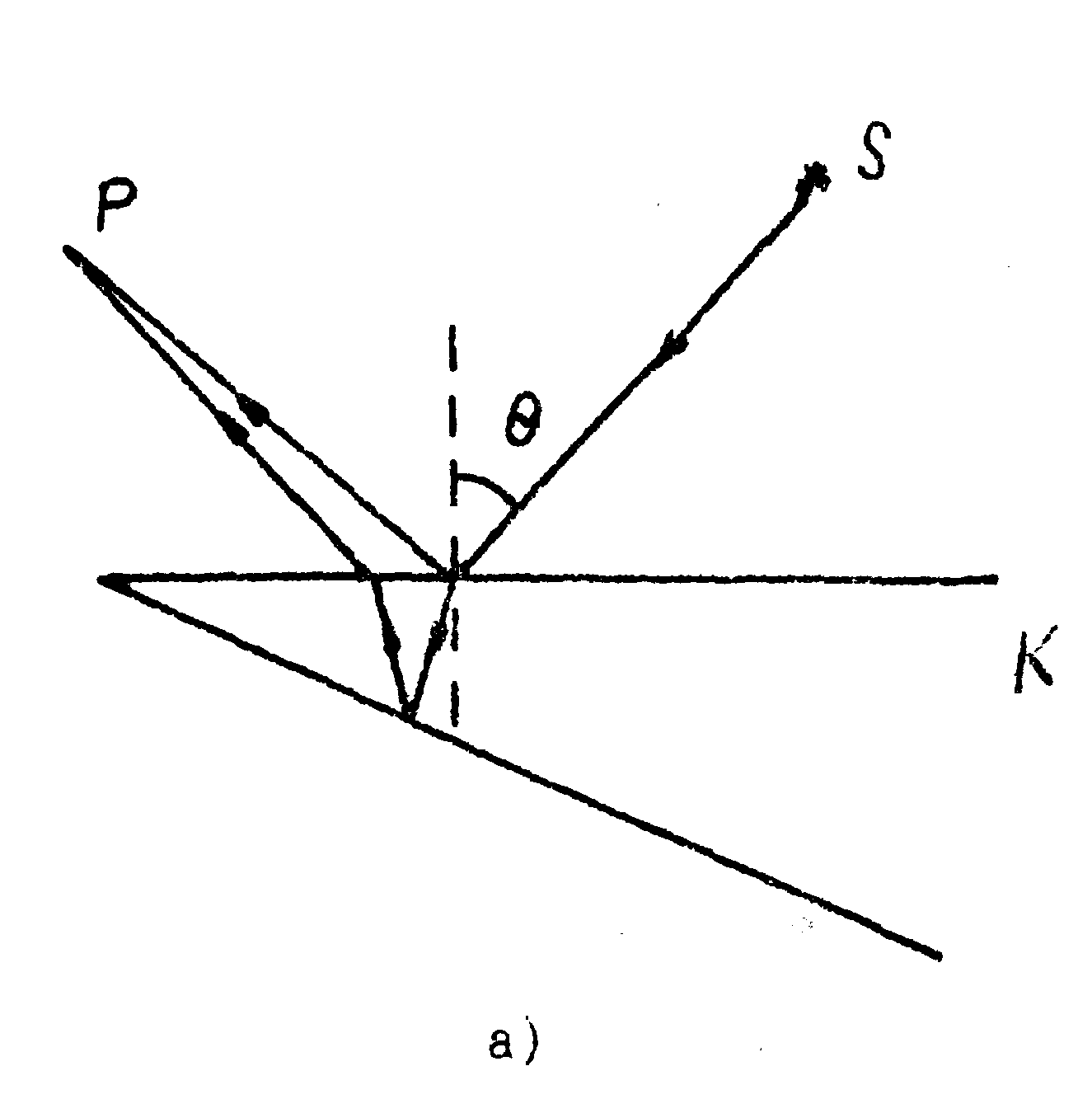
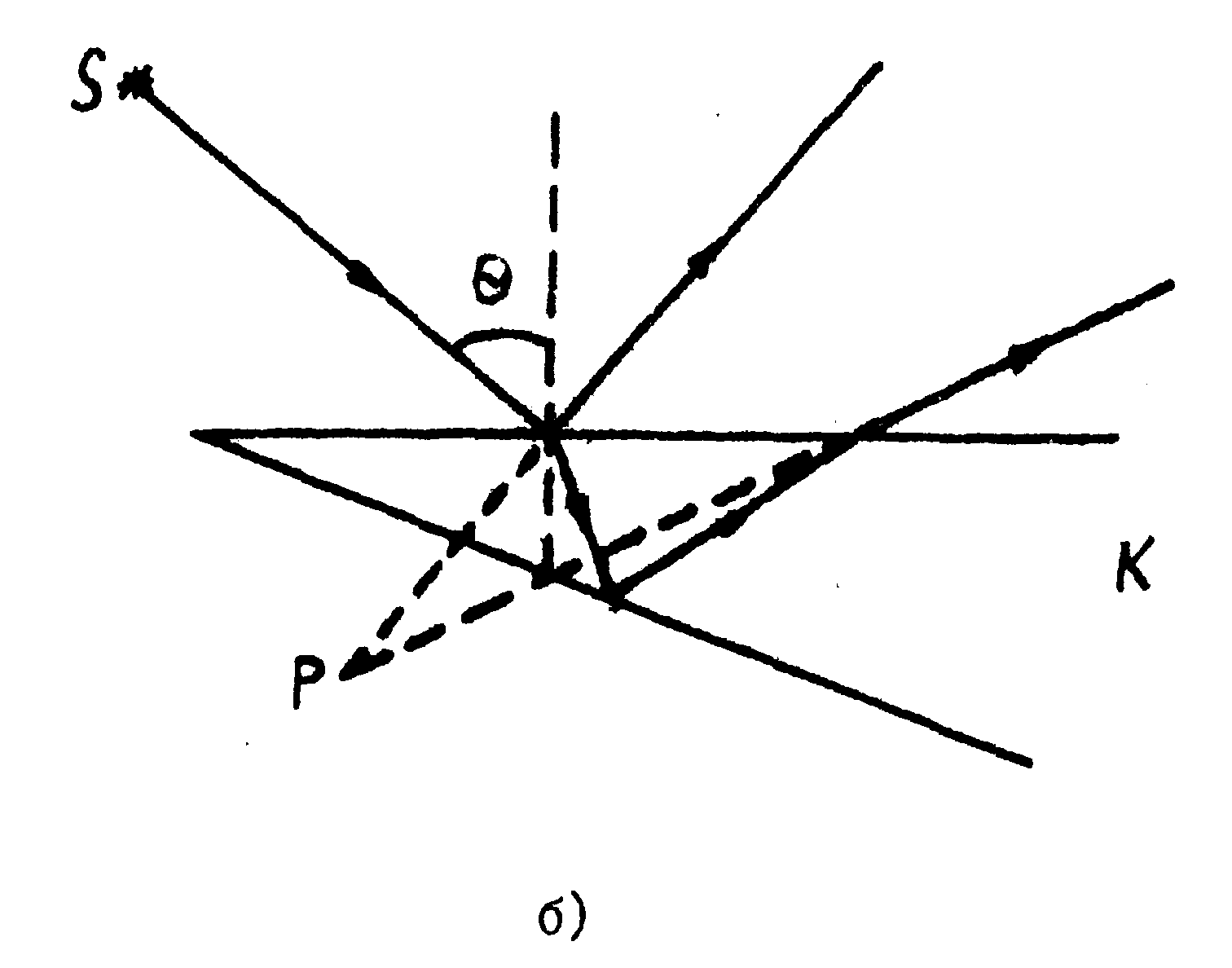
Рис.2. Полосы равной толщины:
s- источник; k- клин; Р- точка, в которой наблюдается интерференционная картина, θ - угол падения.
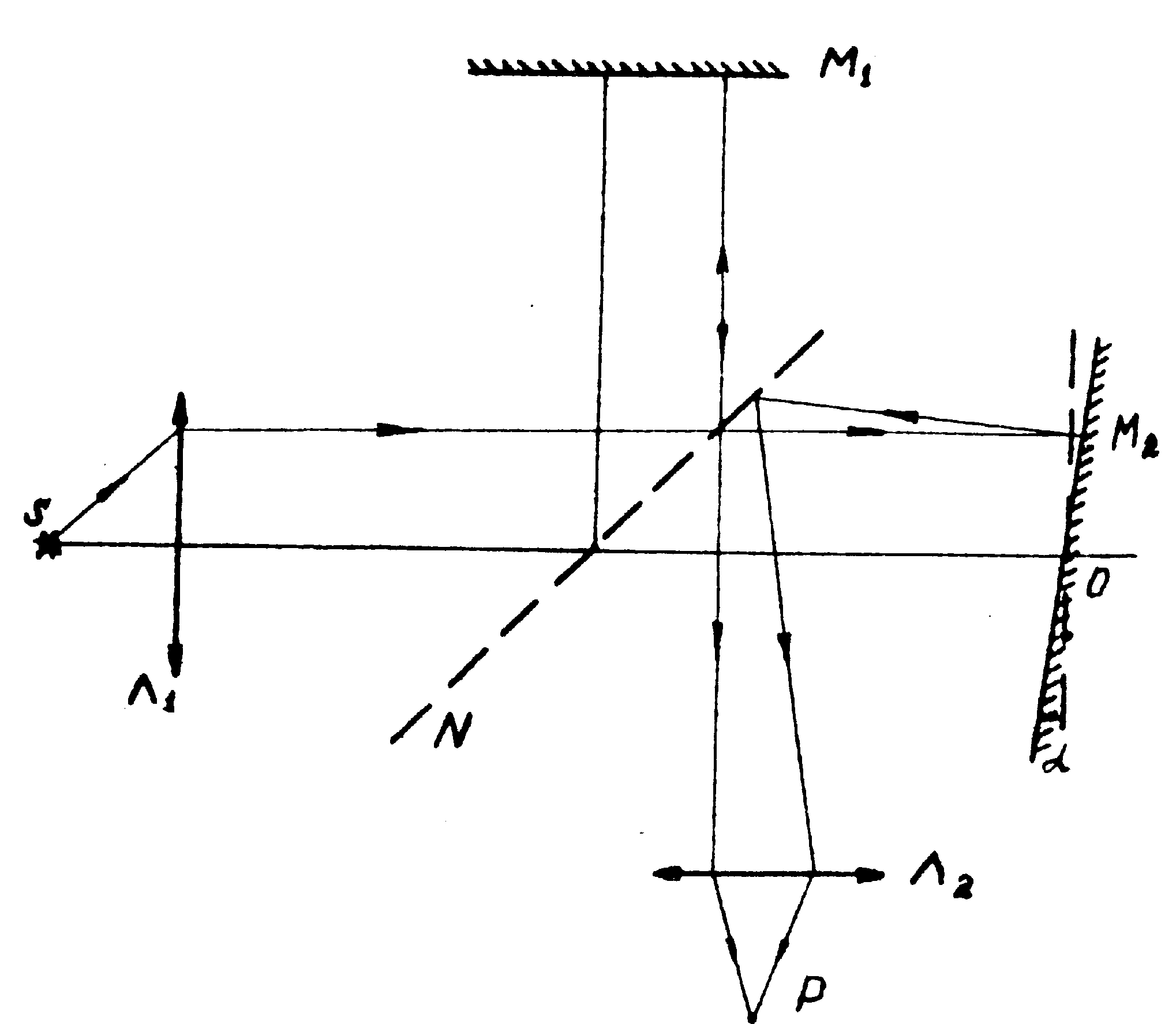
Рис.3. Схема прохождения лучей в интерферометре Майкельсона:
s- источник; Λ1 и Λ2- входная и выходная линзы;
М1 и М2 - зеркала; n - светоделительная пластинка;
Р - точка, в которой наблюдается интерференция.
Интенсивность интерференционных полос i(δ) ξпределяется как
i(δ)~cos2πνδ~cos2πν2xsinα,
где ν- волновое число.
Найдем период функции. Для этого
πνΔδ=πν2Δx sinα=π,
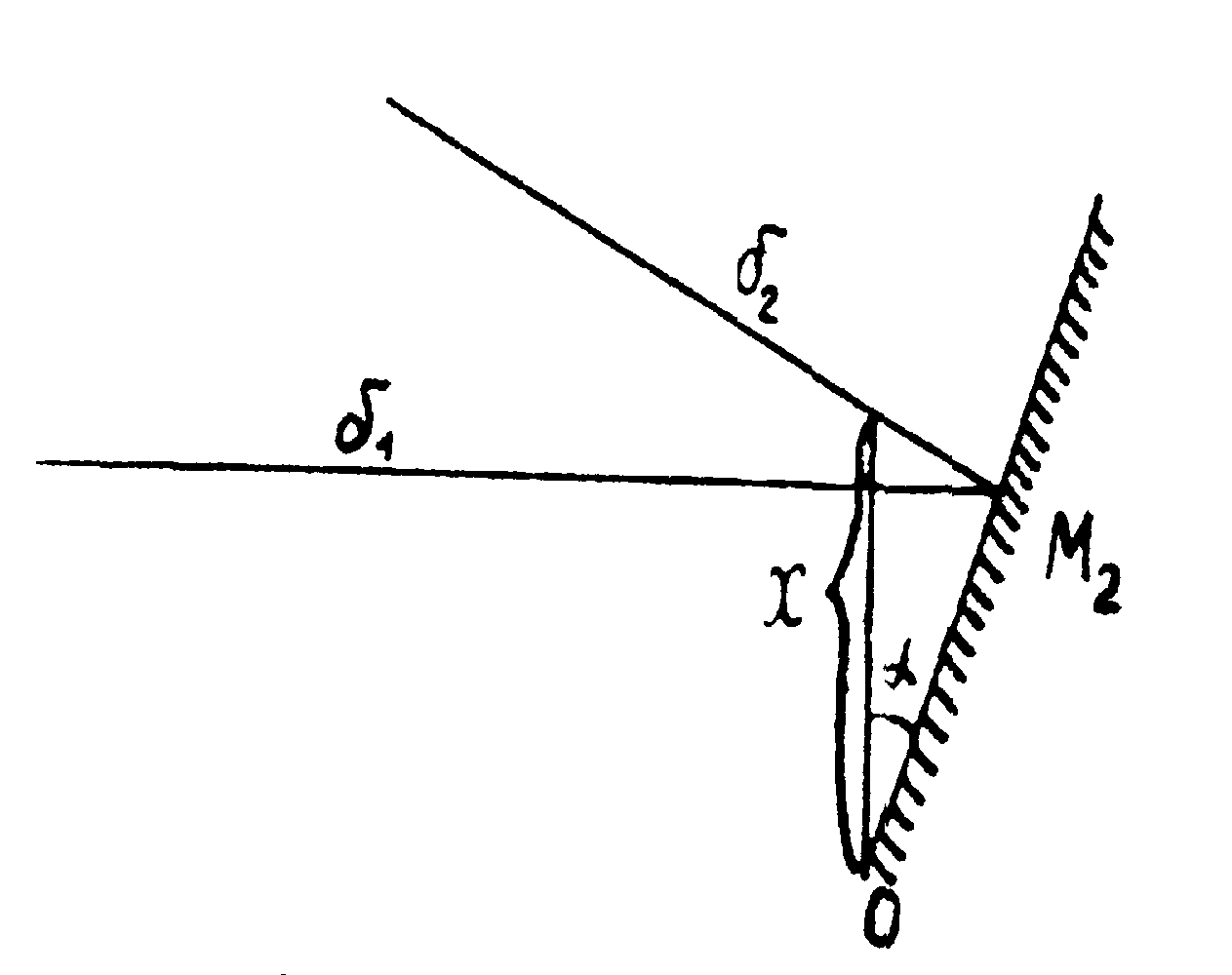
Рис.4. К вопросу о разности хода:
δ1, и δ2 - ход лучей; М2- зеркало; α - угол поворота зеркала от нормального положения.
Откуда
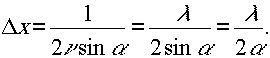
Соответствующая пространственная частота определяется как
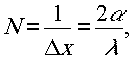
т.е. с увеличением угла поворота α одного из зеркал число полос линейно растёт. В частности, это означает, что так как наблюдение ведётся с помощью глаза ипи линзы, имеющих предельную пространственную частоту, то, начиная с некоторого α, полосы не будут наблюдаться (контрастность упадёт до нуля). С другой стороны, при α→0 полосы расширяются до бесконечности и также ненаблюдаемы.
Отметим, что в первом приближении размеры источника оказывают влияние только на контрастность, а не на положение полос.
Остановимся теперь на образовании полос равного наклона (рис.5). Для этого случая
i(δ)~cos2πνδi,
где δi - разность хода, зависящая от угла наклона i.
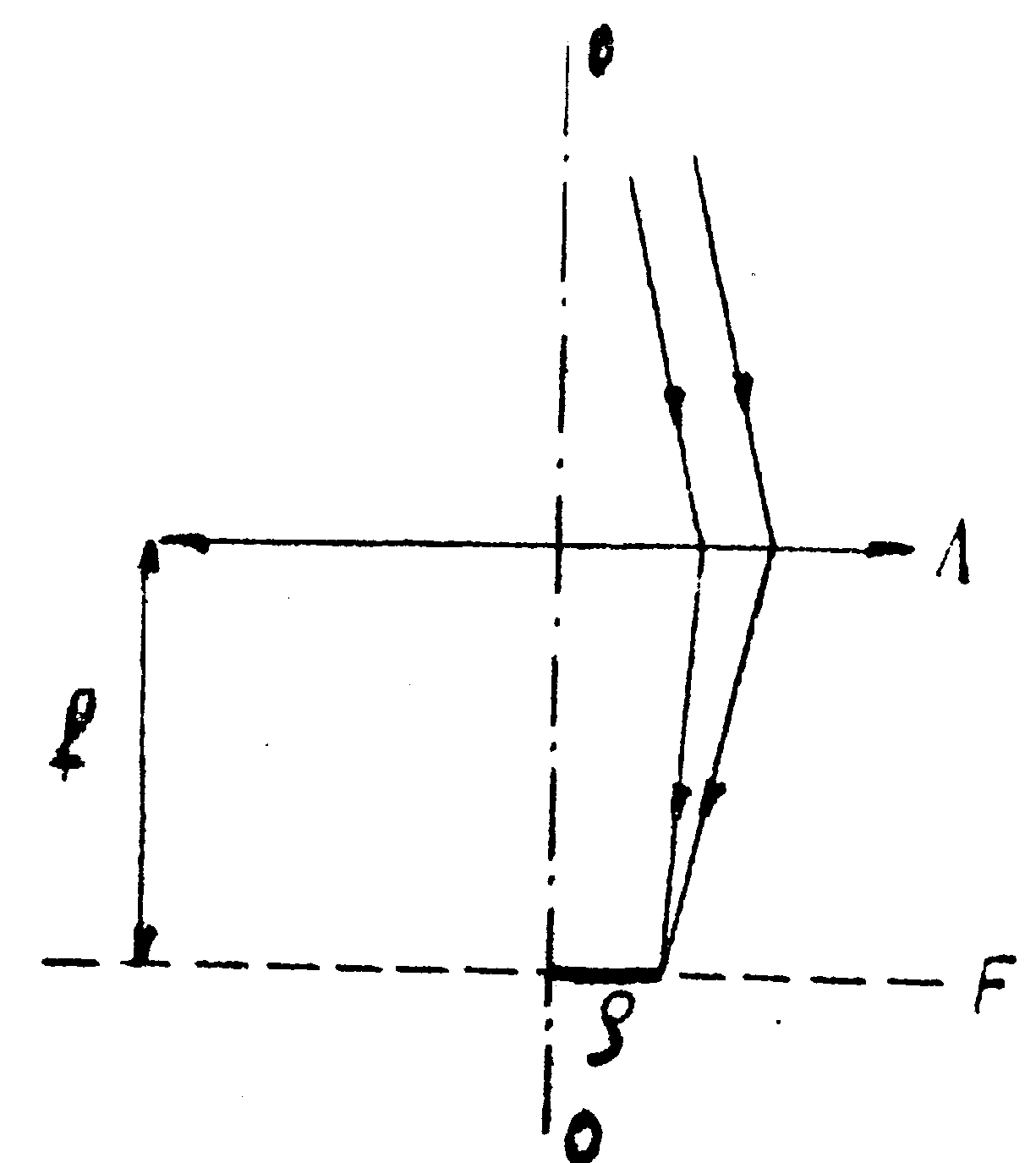
Рис.5. Образование полос равного наклона:
oo - ось симметрии; Λ- линза; f- фокальная плоскость линзы; f- фокусное расстояние; ρ- расстояние между фокусом и точкой интерференции.
По-прежнему интерференционная картина рассматривается в точке Р. f - фокусное расстояние линзы; ρ~ fi - расстояние от точки Р, в которой рассматривается интерференция, до центральной точки картины. .
Так как δi = δ0cos i, где δ0 - разность хода для центрального луча, то
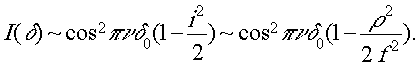
Положим
πνδ0=πκ,
тогда
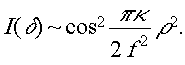
Мы получили систему сходящихся окружностей, причем,чем больше порядок интерференции k, тем меньше расстояние между соседними полосами, важно отметить, что эти полосы возникают только за счёт конечных размеров источника и линза не оказывает на них влияния.
Перейдём к вопросу о контрастности полос. Теория показывает, что закон падения контрастности полос за счёт конечных угловых размеров источника одинаков как в cлyчae регистрации модулированного светового потока в фокусе линзы, так и при фотографировании на пленку распределения интенсивности в полосах равной толщины. Этот закон имеет следующий вид:
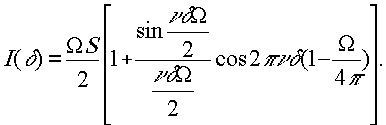
где Ω- телесный угол, стягивающий приёмную площадку. Контрастность полос v определяется как
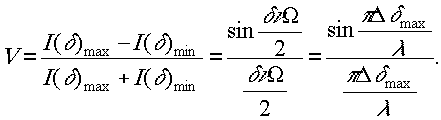
Вспомним, что
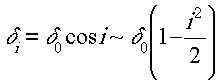 и
и 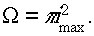
Имеем
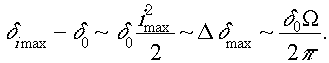
Для зеркал Френеля контрастность падает по аналогичному закону:
Δδmax = de,
где е- линейный размер щели, a d- безразмерный множитель, определяемый геометрией оптической системы.
Найдём теперь связь между числом полос равной толщины и допустимыми угловыми размерами источника. Начиная от нулевой полосы
δ = 0 , θмеем
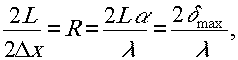
где l - длина зеркала, a r- разрешающей способность.
Из условия 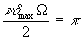 имеем νδmaxΩ=2π
и,так как δmax=rλ/2,
окончательно запишем
имеем νδmaxΩ=2π
и,так как δmax=rλ/2,
окончательно запишем
Ωr = 4π.
Отсюда можно сделать вывод, а именно: число интерференционных полос в интерферограмие и голограмме не может превышать величину
r=4π/Ω.
В заключение рассмотрим вопрос и разрешающей способности
голографического метода. Если рассеянное излучение от голограммы
собираем в первом порядке дифракции, то это эквивалентно применению
преобразования Фурье:
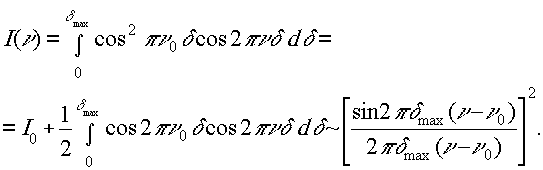
Отсюда разрешение, выраженное в волновых числах, определится как