1. Некоторые интегральные преобразования и их применение

Любая функция однозначно определяется своим преобразованием Фурье или спектром. Функция f(x) и её спектр f(u) образуют пару преобразований Фурье

f(x)=∫f(u)exp-i2πxudu,

f(u)=∫f(x)expi2πxudx,

где вектор х - пространственные координаты, вектор u- пространственно-частотные координаты, хu - скалярное произведение векторов х и u. Для функций, заданных на плоскости, векторы x и u имеют по две составляющих x=(x,y), u=(u,v) и скалярное произведение векторов имеет вид:

а дифференциалы dx и du, соответственно;

Переход от функции, заданной на плоскости, к ее спектру технически выполнить значительно труднее, чем в случае одноразмерной функции. Дело в том, что аналоговых двухразмерных анализаторов спектра практически не существует, а использование вычислительных машин затруднено, во-первых, из-за необходимости переходить к дискретному по пространству заданию функций и, во-вторых, из-за значительно большего объёма дискретных данных (и необходимого времени счёта) в случае двухразмерных функций. На основе оптических систем могут быть созданы аналоговые двухразмерные анализаторы пространственного спектра, причём быстродействие таких анализаторов может быть очень большим.

r(Δx)=∫f(x)f^*(x-Δx)dx

или преобразование Фурье от функции корреляции - так называемый энергетический спектр поля f (х) (звёздочкой обозначена кошыекс-носопряжённая величина). Энергетический спектр поля равен квадрату модуля спектра поля

r(u) = |f(u)|² = |∫f(x)expi2πxudx|².

При оценке спектра случайного поля необходимо выполнять ещё одну интегральную операцию: сглаживание энергетического спектра r(u) некоторой функцией Г(u)

∫r(v)Г(u-v)dv.

Сглаживанию спектра соответствует умножение функции корреляции r(Δx) на действительную чётную функцию γ(Δx), причём функции γ(Δx) и Г(u) образуют пару преобразований Фурье.

Несколько слов о способе задания исходной функции f(x). Будем считать, что f(x) соответствует распределению амплитуд светового поля, т.е., например, плоский полупрозрачный транспарант имеет коэффициент пропускания света по амплитуде, пропорциональный f(x). f(x) может быть комплексной функцией.

Эти трудности удаётся обойти, если задавать исходную функцию в виде коэффициента пропускания света по интенсивности (энергетического коэффициента пропускания). Энергетический коэффициент g(х) плоского полупрозрачного транспаранта связан с амплитудным коэффициентом f(x) соотношением g(x)=|f(x)|².

Произвольная линейная оптическая система полностью определяется импульсной реакцией или откликом на δ-образное воздействие m(х,х₁). Функция m(х,х₁) описывает распределение амплитуд светового поля в выходной плоскости х, оптической системы при точечном распределении амплитуд на входной плоскости x (на входе системы), причём координата x есть координата условного точечного источника света на входе системы. Импульсная реакция системы, как и любое распределение амплитуд света, может быть измерена только косвенно. Однако для простых линейных систем импульсная реакция мояет быть найдена теоретически.

Исходная функция задана на плоском полупрозрачном транспаранте в виде распределения амплитудного коэффициента пропускания света f(x). Транспарант совмещается с входной плоскостью оптической системы. Освещение транспаранта задаётся мгновенным распределением амплитуд a(x,t) на входной плоскости (освещение квазимонохроматическое).

m(x,t) =∫a(x,t) f(x) m(x,x₁) dx.

После усреднения по времени получаем распределение интенсивности света n(х₁) в выходной плоскости, которое может быть измерено или зафиксировано

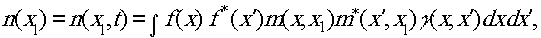
где γ(х,х') = a(x,t)a*(x^|,t) - коэффициент пространственной когерентности света на входной плоскости (черта сверху означает усреднение по времени) /1/.

5. Импульсные реакции двух оптических систем

Система, состоящая из одной сферической линзы, может выполнять преобразование, сходное с дифракцией Фраунгофера. Поэтому будем условно называть такую систему дифракционной. Сферическая линза превращает сферические волны, исходящие из точек передней фокальной плоскости, в плоские. Легко показать, что точечный монохроматический источник света с координатами х в передней фокальной плоскости линзы создает в задней фокальной плоскости распределение амплитуд

где хu- скалярное произведение векторов х и u, u = x₁/λl - пространственно-частотные координаты в выходной плоскости, l -фокусное расстояние линзы, λ - длина волны света. Знак в показателе экспоненты зависит от выбора направления осей координат х и u и может быть любым. Таким образом, импульсная реакция однолинзовой оптической системы совпадает с ядром преобразования Фурье.

m(x,u) = expi2πxu+exp-i(2πxu+ψ)=cos(xu+ψ/2),

где ψ - оптическая разность хода дчя лучей от объекта f (x) и его зеркального изображения f(-x). Фаза ψ не зависит от координат х и u и может изменяться от 0 до 2π путём перестройки оптической системы. Один из вариантов построения интерференционной системы рассмотрен, например, в /2/.

4. Пространственная когерентность света

Для однолинзовой осветительной системы существует простая связь между коэффициентом пространственной когерентности света и распределением интенсивности света по источнику. Каждая точка теплового квазимонохроматического источника света, помещённого в передней фокальной плоскости u, излучает свет с мгновенной амплитудой. В задней фокальной плоскости x линзы волна превращается в плоскую

b(u,t)ехр-i2πxu, так что мгновенное распределение амплитуд в задней фокальной плоскости равно

a(x,t)=∫b(u,t)exp-i2πxudu.

γ(x,x^|) = a(x,t) a^*(x^|,t) = ∫b(u,t) b(u^|,t)exp-i2π(xu-x^|u^|)dudu^|.

только при совпадении координат u и u^|. Благодаря фильтрующему действию δ-функции получаем

γ(x,x^|) = ∫ Г(u)exp-i2π(x-x^|)udu.

Коэффициент когерентности света равен преобразованию Фурье от распределения интенсивности света Г(u) по плоскому тепловому источнику /3/.

5. Преобразование объекта в дифракционной системе

Для создания когерентного освещения может использоваться точечный тепловой источник, расположенный на оси осветительной однолинзовой системы. При этом Г(u) = δ(u), γ(υ)=1. Распределение интенсивности на выходе дифракционной системы получает вид:

n(u) = |∫f(x)expi2πxudx|² = ∫r(x)expi2πxudx = r(u),

т.е. формируется квадрат спектра функции f(х) или, иными словами, энергетический спектр функции f(x), или спектр корреляционной функции r(Х).

n(u) = ∫r(x)γ(x)expi2πxudx = ∫r(v)Г(u-v)dv,

то есть выходное распределение равно энергетическому спектру функции f(x), сглаженному с помощью фильтра, частотная характеристика Г(u) которого совпадает с распределением интенсивности света по тепловому источнику света. Операция сглаживания энергетического спектра позволяет выполнять оценивание энергетического спектра случайного поля f(x), заданного в виде амплитудного коэффициента пропускания света входным транспарантом.

Особый интерес представляет преобразование функции f(x) в том случае, когда имеется дополнительный опорный источник света, уда-

ленный от начала координат на входной плоскости. Объект и опорный источник можно рассматривать как новый объект f(х)+δ(x-x₁) exp iφ где φ - изменение фазы света при прохождении точечного отверстиями использовать имеющееся соотношение для его преобразования. При когерентном освещении распределение интенсивности света в выходной плоскости получает вид:

n (u) = r (u) + |f(u) cos (ux₀ + Ф - φ) + const,

где Ф - фаза комплексного спектра f(u). Это распределение является Фурье-голограммой объекта f(х). Таким образом, голограмма может рассматриваться как частный случай интегрального преобразования n(u)=r(u). Голограмма состоит из двух частей, наложенных друг на друга: энергетического спектра r(u), образующегося в результате взаимодействия света от каждой точки объекта со светом от всех других точек (освещение пространственно когерентное), и спектра f(u) в виде узкополосной функции частотных координат, образующегося в результате взаимодействия света от всех точек объекта со светом от опорного источника. Периодическая структура второй составляющей голограммы позволяет отделить при восстановлении изображение объекта, создавшего распределение амплитуды f(x), от изображения корреляционной функции r(х). Восстановление производится при освещении Фурье-голограммы параллельным пучком пространственно когерентного света.

6. Преобразование объекта в интерференционной системе

При некогерентнои освещении коэффициент когерентности равен δ -функции, фильтрующее свойство которой позволяет найти распределение на выходе интерференционной системы:

n(u) = ±re g(2u) + const при ψ = 0, π,

n(u) = ±im g(2u) + const при ψ = π/2, 3π/2,

где g(u) =∫q(x)expi2πxudx - пространственный спектр объекта q(х), являющегося энергетическим коэффициентом пропускания света

исходным транспарантом; re g(2u) - вещественная часть спектра g(2u), равная спектру центрально-симметричной чётной фигуры q(х) + q(-х) (объект q(х)), и опорное изображение q(-x); im g(2u) - мнимая часть спектра g(2u), равная спектру центрально-симметричной нечётной фигуры q(x) - q(-x). Преобразование для энергетического коэффициента удобно тем, что преобразование при этом не зависит от фазовой структуры транспаранта и, кроме того, удобнее иметь дело с энергетическим коэффициентом, так как все оптические измерения ведутся по энергии, а не по амплитуде.

Распределение интенсивности света на выходе интерференционной системы может приобретать периодическую структуру, подобную структуре когерентной голограммы, если исходный объект q(х) сместить относительно начала координат (оси системы) во входной плоскости. Смешённый объект характеризуется коэффициентом передачи q(x - x₀). При этом выходное распределение интенсивности света получает вид (некогерентное освещение):

n (u) = |g(2u)|Соs(2uх₀ + Ф + ψ) + const,

где Ф - фаза комплексного спектра g(2u).

Периодическая структура не является принципиально необходимой для некогерентной голограммы, так как она включает в себя только изображение пространственного спектра объекта и не содержит изображения спектра свертки объекта. Это обстоятельство не отмечается в работах по некогерентным голограммам /4,5/.

Экспериментально получены и обсуждаются только некогерентные голограммы с периодической структурой, что связано с применением пространственно когерентного света при восстановлении^*.

Более естественно и логично производить восстановление путём повторного построения некогерентной голограммы от имеющейся некогерентной голограммы объекта /2,6/, при вторичном голографировании выполняется обратное преобразование Фурье над распределением интенсивности (прямое и обратное преобразования Фурье различаются лишь условным направлением осей координат). Получаемое изображение является простой фотографией объекта. Для восстановления может использоваться или полная голограмма, или половина (в последнем случае вторая половина формируется в зеркальной системe как опорное изображение). Центр симметрии голограммы при восстановлении должен совпадать с осью зеркальной системы. Таким образом, имеется возможность многократного последовательного выполнения преобразования Фурье, причём в качестве исходного объекта для очередного преобразования может использоваться изображение (транспарант), полученное на выходе интерференционной системы при предыдущем преобразовании.

При построении некогерентной голограммы от объекта с резкими перепадами интенсивности в некоторых случаях может быть уменьшен динамический диапазон регистрирующего материала по сравнению с динамическим диапазоном интенсивностей исходного объекта.

1) формирование энергетического пространственного спектра функции f(х) (амплитудного транспаранта) с помощью дифракционной системы при пространственно-когерентном освещении и, как частный случай, формирование пространственного спектра функции f(х) в виде узкополосной функции пространственных координат (когерентная голограмма);

2) Формирование сглаженного энергетического спектра функции f(х) при частично когерентном освещении;

3) формирование действительной и мнимой частей пространственного спектра функции f(x) (энергетического транспаранта) в интерференционной системе при пространственно-некогерентном освещении и, как частный случай, формирование пространственного спектра функции q(х) в виде узкополосной функции пространственных координат.

Кроме того, при иных условиях освещения могут выполняться некоторые другие интегральные преобразования специального вида.

Л и т е р а т у р а

2. К.В.Коняев. physics letters, 24a, № 9, 490 (1967).