Media-security

ОБЩИЕ СВОЙСТВА ТРЁХМЕРНЫХ ГОЛОГРАММ

В.Ш.Шехтман

Вводная часть лекции посвящена связи меджу голографией и рентгеноструктурным анализом.

Возникновение голографии, как нового метода создания оптического изображения естественным образом, приводит к желанию использовать эти принципы и в рентгеновской диапазоне. В настоящее время известно, что осуществлению рентгеновской голографии препятствует трудности, которые являются, если не принципиальными, то по крайней мере техническими. Однако связь между рентгеноструктурным анализом и голографией не исчерпывается проблемой рентгеновской голографии.

Могут быть сформулированы следующие направления работ, объединяющие голографию и рентгеноотруктурный анализ:

а) получение голограмм в рентгеновском диапазоне (решение фазовой проблемы в рентгеноструктурном анализе);

б) анализ свойств трёхмерных голограмм на основе теории дифракции рентгеновских лучей;

в) использование голограммы, полученной в оптическом диапазоне, в качестве модельного объекта для исследования явлений дифракции на совершенных кристаллических структурах.

Разделы б) и в) демонстрируют взаимное проникновение принципов голографии и рентгеиоотруктурного анализа. Как будет показано ниже, такое взаимодействие может оказаться полезным.

Указанные вопросы будут рассмотрены в следующей последовательности:

1) аналогия между рентген оструктурным анализом и голографией;

2) структура трёхмерной голограммы и анализ процесса реконструкции.

1. Аналогия между рентгеноструктурным анализом и голографией

Рентгеноструктурный анализ так же, как и голография, основывается на двухступенчатой схеме (двухкратное преобразование Фурье). Если исходить из задачи определения ранее неизвестной кристаллической структуры, эта аналогия иллюстрируется схемой процессов, изображенных на рис.1.

Таким образом, первой стороной является аналогия операциональная. Операция "чтения" в голографии и дешифровки структуры в РСА совпадают принципиально. В работе /1/ было показано, что реконструкция голограммы и синтез автокорреляционной функции (функции Паттерсона) полностью совпадают.

При переходе к трёхмерным голограммам с необходимостью возникает другая сторона аналогии. Известно, что голограмма, записанная в некотором объёме - на трёхмерном светочувствительном элементе, - может быть представлена как набор элементарных трёхмерных периодик. Тогда процесс "чтения" трёхмерной голограммы следует анализировать так же, как процесс регистрации рентгенограммы, что иллюстрируется схемой рис.2. Отметим, что все последующее изложение ведётся в терминах голографии Фурье-Фраунгофера.

В оптических системах видимого диапазона процессы дифракции на объёмных структурах не анализируются. Естественно поэтому при изучении процессов реконструкции трёхмерных голограмм обратиться к теории рентгеноструктурного анализа, возникшей с самого начала на основе задачи о дифракции на трёхмерной периодической системе осцилляторов. Видимо, не требуется обоснования специфических отличий дифракции на трёхмерных структурах, поскольку это и составляло предмет открытия Лауэ.

Следует только подчеркнуть и напомнить, что основным отличием трёхмерных решёток от двух- и одномерных является высокая избирательность и критичность по отношению к углу падения первичного луча. Дифракционные максимумы возникают только в случае падения лучей под фиксированными углами, определяемыми уравнением Вульфа-Брегга.

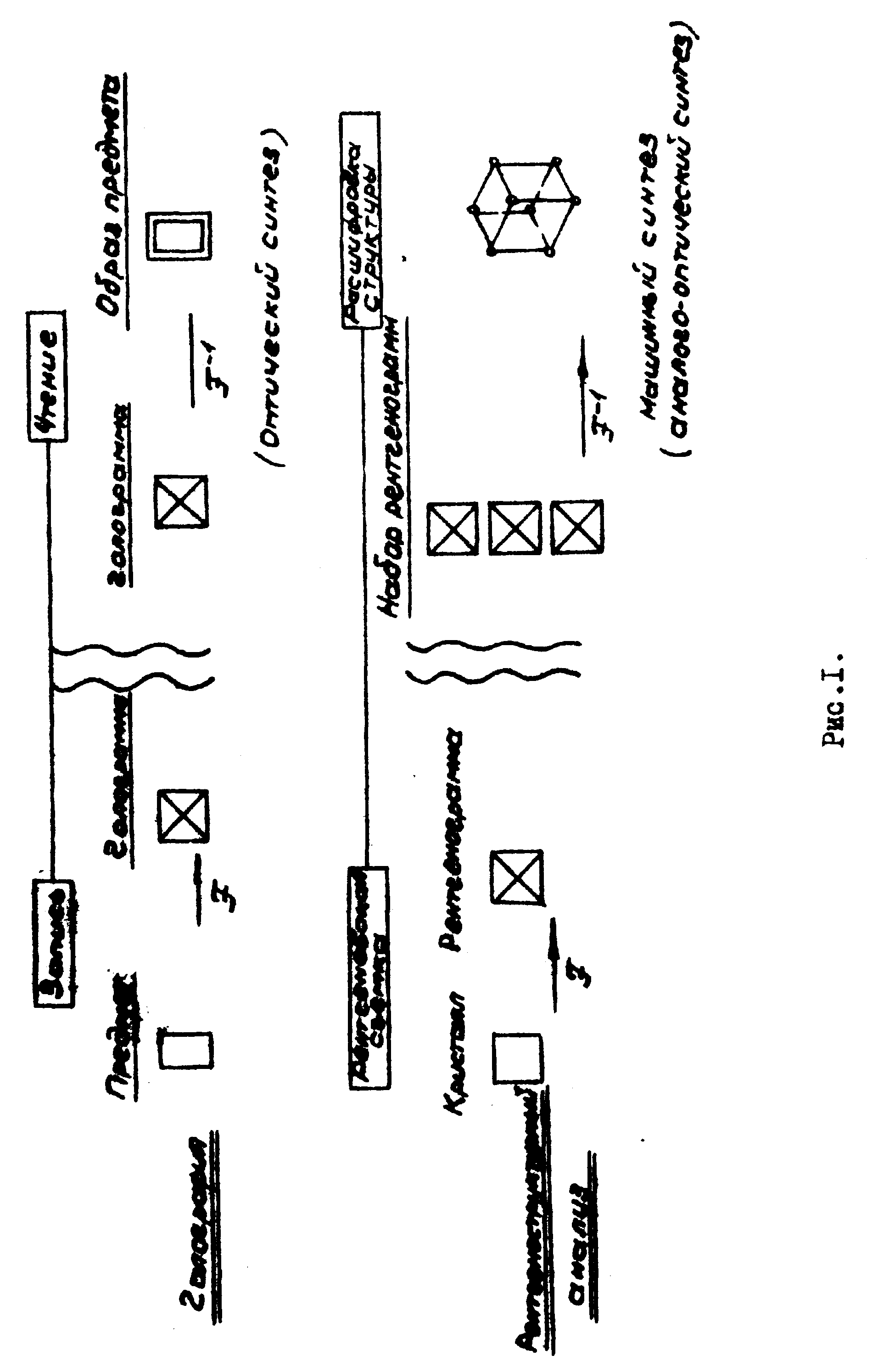
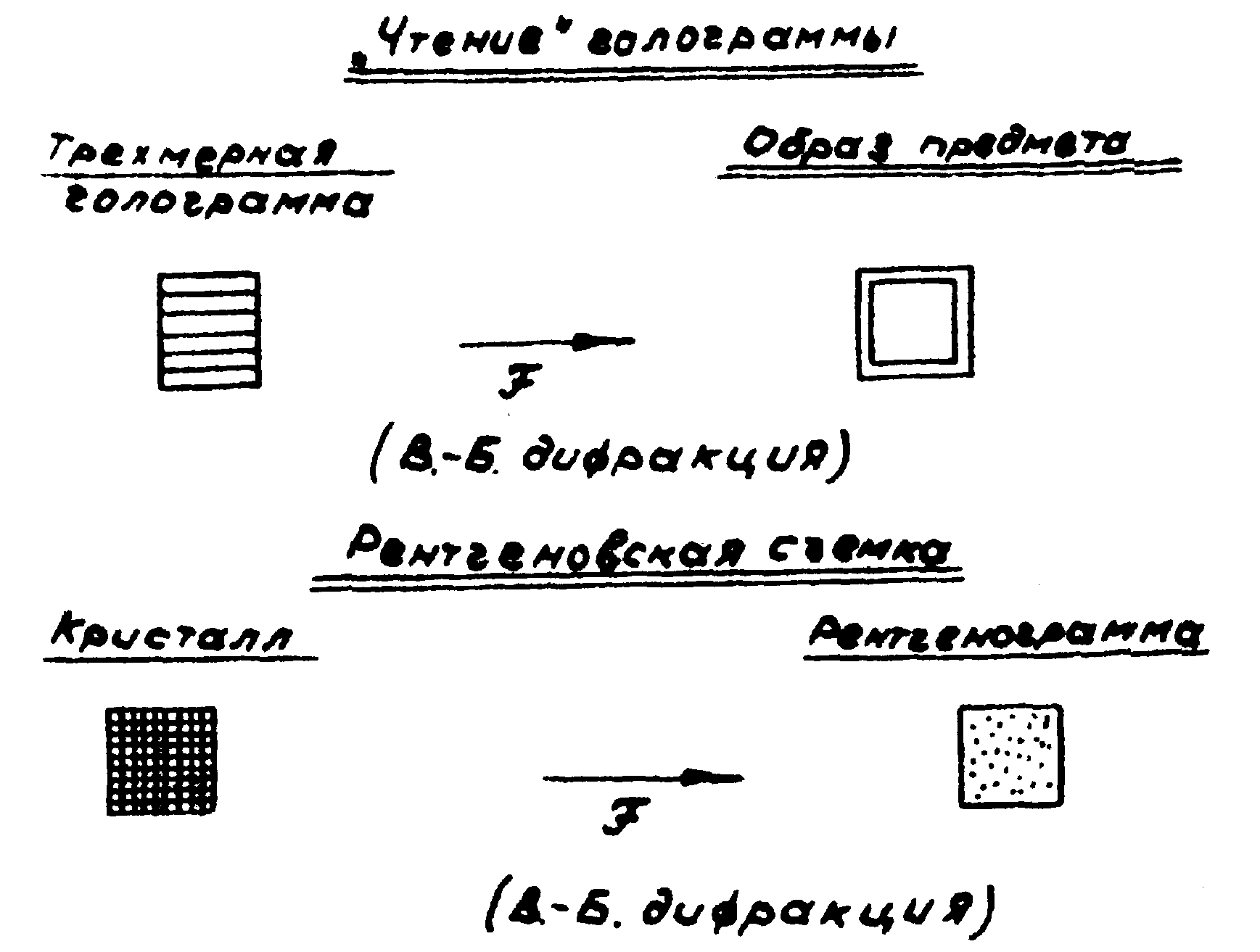
Рис.2.

Таким образом, второй стороной аналогии начнется подобие процесса реконструкции трёхмерной голограммы и явлений дифракции в рентгенографии.

Необходимо заранее оговорить, что в принципе всякая голограмма, поскольку она фиксируется на фотоэмульсии конечной толщины, может рассматриваться как трёхмерная. Это означает, что рассматриваемые ниже специфические свойства трёхмерных голограмм в определённых условиях могут наблюдаться и даже становиться существенными уже при использовании обычных "тонкослойных" фотопластинок.

Анализ голографических схем показывает в известных экспериментах Ю.Н.Денисюка /2/, что влияние трёхмерности фоточувствительного слоя проявляется более заметным образом, чем в схеме Лейта и Упатниекса.

Наше рассмотрение будет в основном относиться к тем голограмммам, у которых толщина соизмерима с линейными размерами апертуры. При этом предполагается, что размеры голограммы значительно превышают период элементарных гармоник.

2. Структура трёхмерной голограммы

и анализ процесса реконструкции

Изложение данного раздела полезно провести, используя аппарат и терминологию теории рентгеноструктурного анализа и, в частности, построение в обратном Фурье-пространстве. Это позволит нам наглядным образом интерпретировать различные экспериментальные схемы и рассмотреть часть свойств трёхмерных голограмм.

На рис.5 в качестве примера приведено построение в обратном

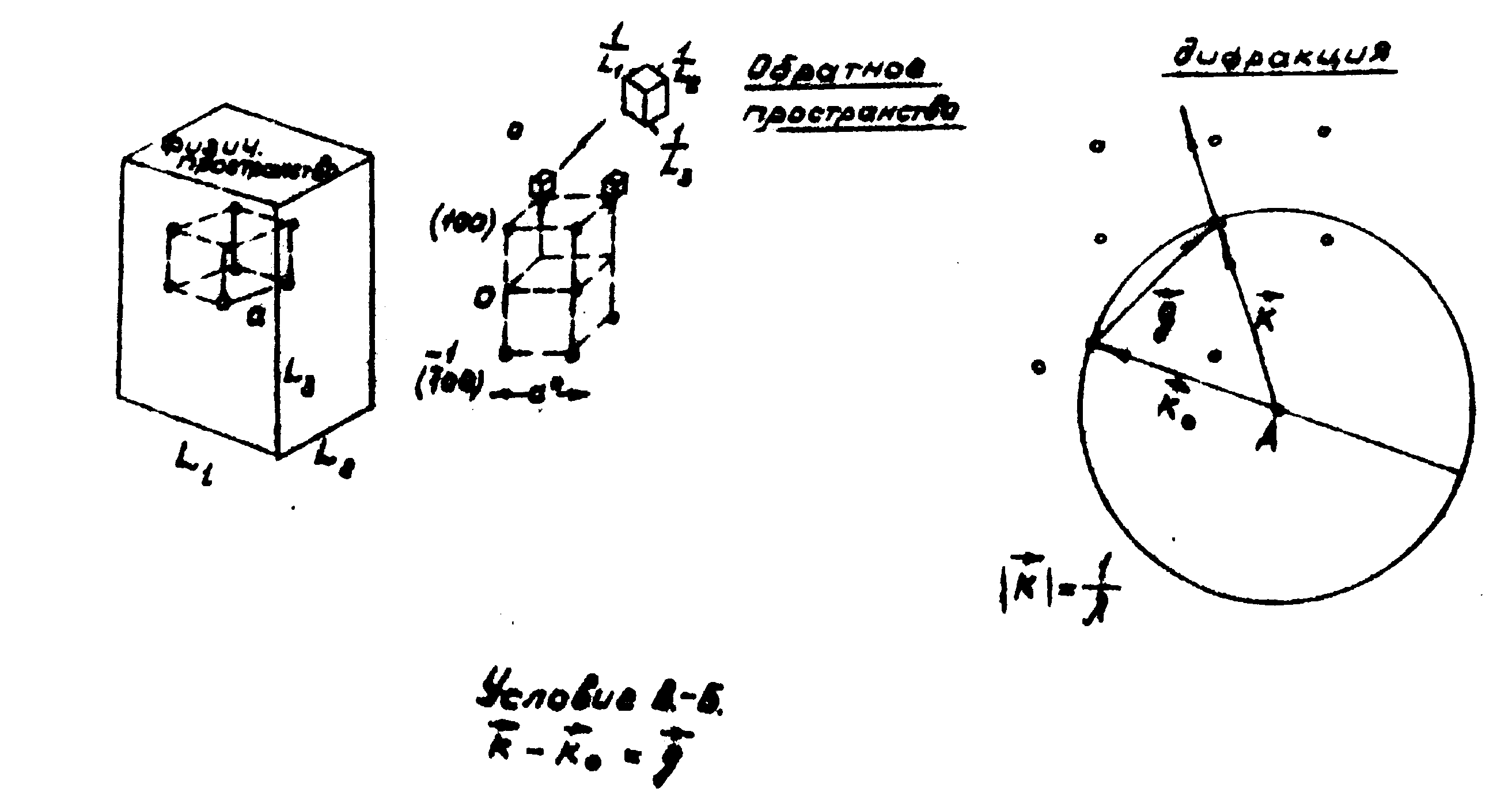
Рис. 3. Построение Эвальда.

l₁, l₂, l₃ - размеры кристалла,

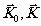- волновые вектора падающей к дифрагированной волны соответственно,

g - вектор обратной решетки.

пространстве (известное под названием построения Эвальда), иллюстрирующее условия появления дифракционных максимумов при рассеянии рентгеновских лучей на кристалле.

Подобные построения позволяют, не выписывая каждый раз аналитических соотношений, рассмотреть основные геометрические особенности явлений дифракции, осуществляемых в эксперименте.

Рассмотрим теперь процесс записи на объёмном светочувствительном элементе и последующий процесс реконструкции на элементарном примере (рис.4.).

Пусть предмет состоит из двух когерентно светящихся точек и регистрация производится в дальнем поле. Полученная голограмма представляет собой предмет, имеющий периодическое распределение пропускания. Вдоль направления типа А'А это распределение является синусоидальным. Такая синусоидальная объёмная решетка даёт лишь (+1) и (-1) порядки отражения. Рассмотрим теперь процесс реконструкции (рис.5). Из построения следует, что для восстановления образа предмета (две точки) необходимо соблюсти геометрические условия процесса записи. То есть читающим источником может служить одна из точек предмета.

Для того, чтобы распространить подобные соображения на предмет произвольного вида, необходимо рассмотреть ещё случай чтения голограммы, полученной от трёх точек (рис.6).

Из построения следует, что существует три варианта восстановления образа предмета: путём освещения голограммы под углом, соответствующим точке 1, 2 или 3. В каждом случае на сферу Эвальда укладывается три узла (один из которых находится в начале координат) обратной решётки. Это соответствует получению трёх дифрагированных лучей и, следовательно, изображения предмета.

Таким образом, восстановление трёхмерной голограммы, записанное от произвольного предмета, соответствует одновременному выполнению условий Вульфа-Брегга для всех элементарных периодик, из которых состоит голограмма.

Произвольное направление луча не приведет к восстановлению изображения. Тем самым устанавливается первое свойство трёхмерной голограммы.

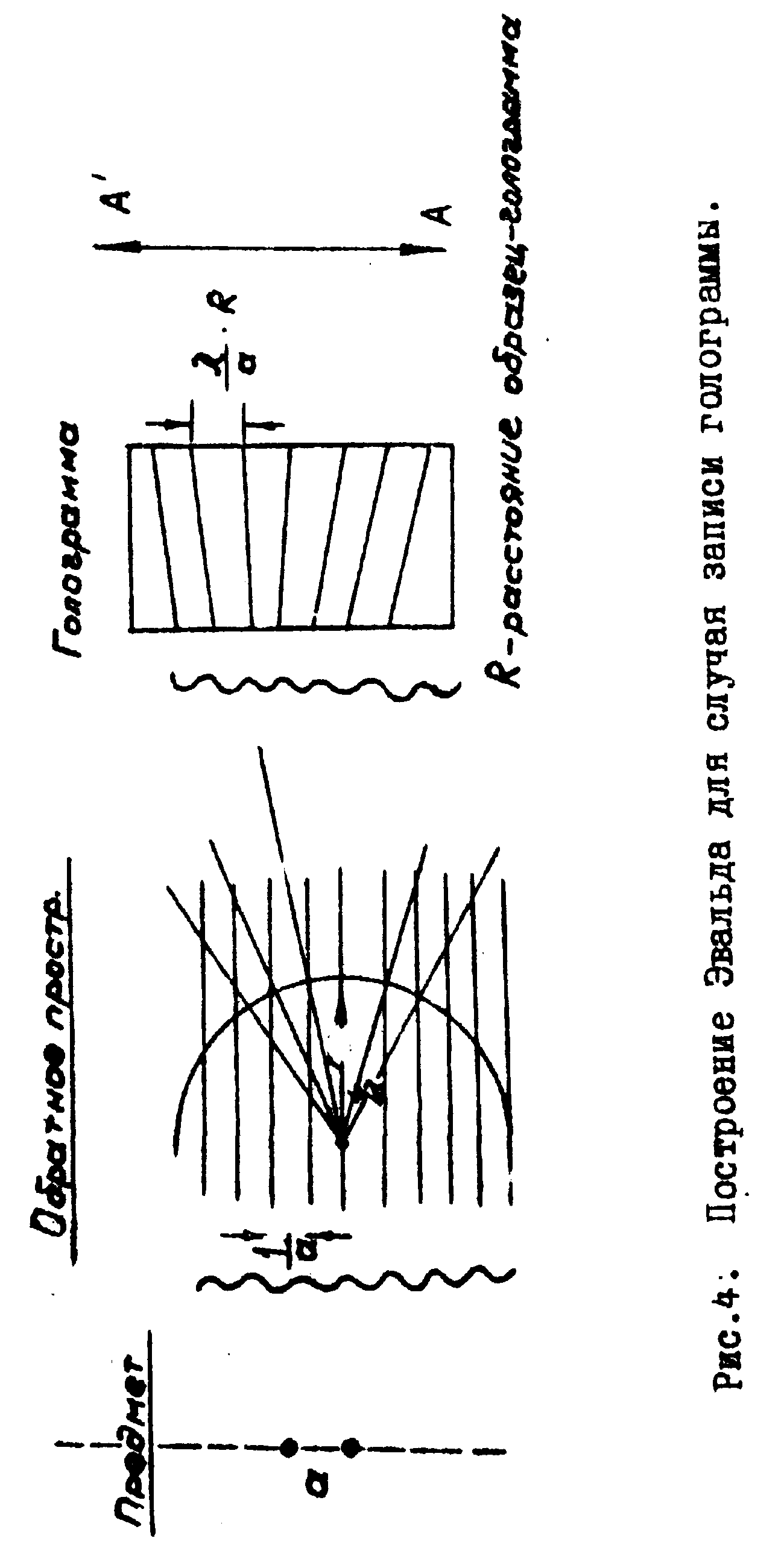
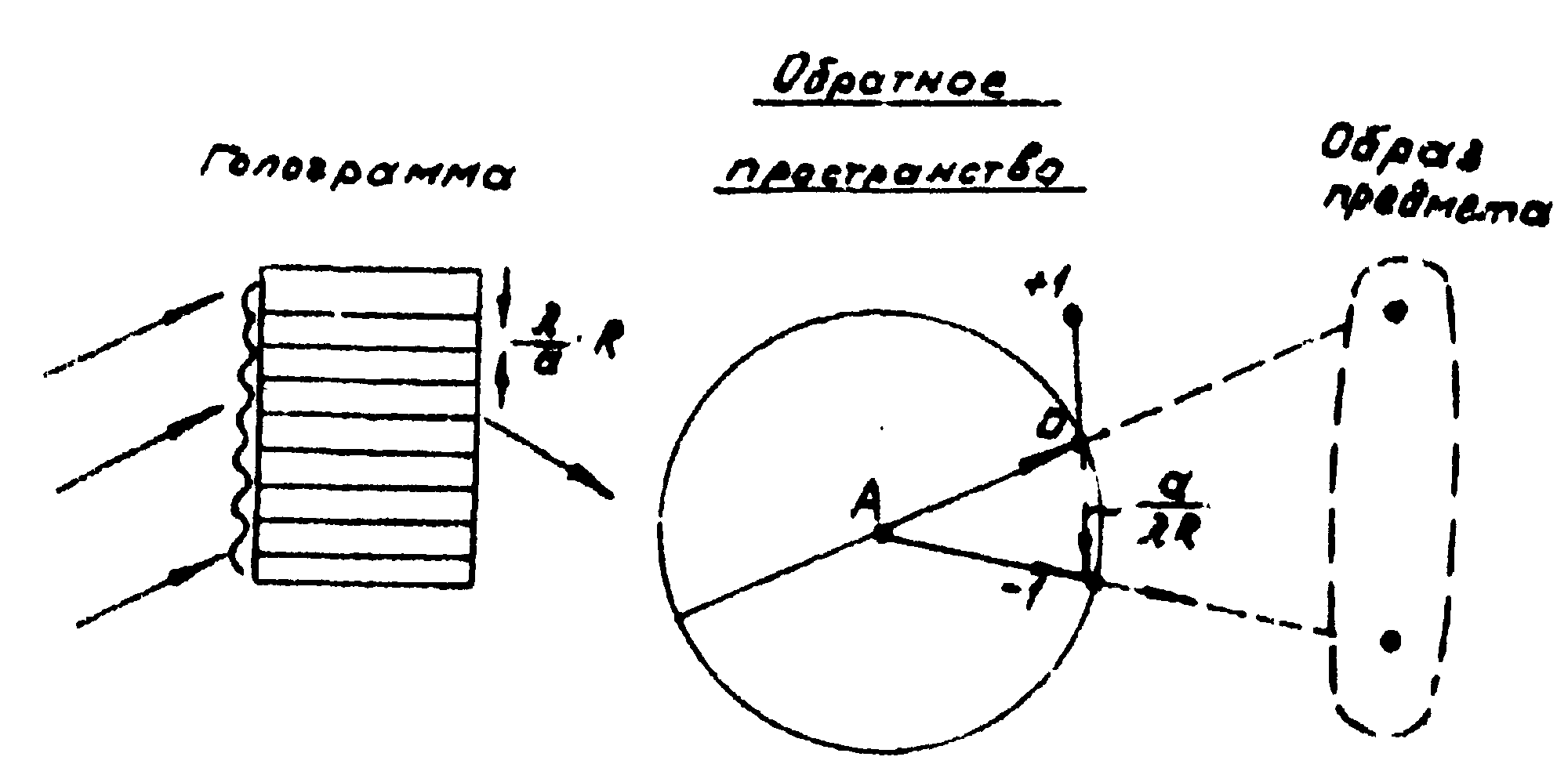
Рис.5. То же построение для случая реконструкции голограммы.

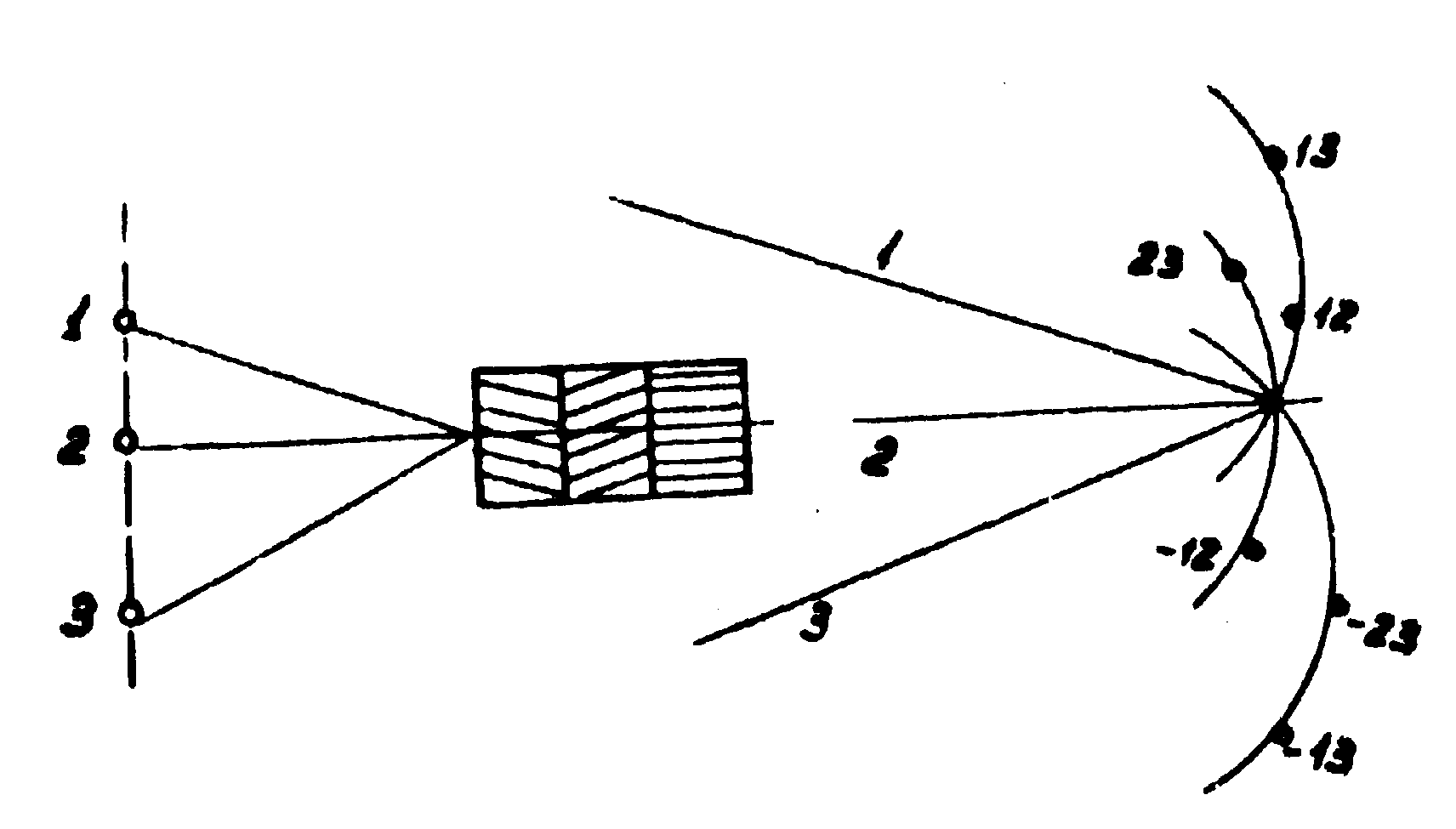
Рис.6. Реконструкция голограммы, записанной от трёх точек (1,2,3). Узлы обратной оешётки 12,15,23 и т.д. соответствуют трём элементарным гармоникам, изображенным для наглядности в трёх прямоугольниках.

Очевидно, что подобное же рассмотрение пригодно и для предмета, являющегося непрерывный распределением светящихся точек. Кроме того, из рассмотрения чертежа следует, что одновременное освещение голограммы из двух точек (например, 2 и 5) приведет и восстановлению того же изображения предмета. Таким образом, устанавливается второе свойство: возможность восстановления изображения путём освещения голограммы протяжённым источникам, совпадающим с частью предмета. Соответствующие выражения, описывающие распределение яркости по предмету, приведены в рабо те авторов /3/.

Следует отметить, что трёхмерная голограмма представляет возможность при определённых условиях использовать в процессе реконструкции протяжённый источник произвольной формы. Для этого требуется, чтобы записывающий источник представлял собой некоторую непрерывную совокупность светящихся точек.

Геометрическая схема, которая поясняет принцип возникновения контраста при использовании для чтения произвольного протяженного источника, приведена на рис.7а. Условия "Вульфа-Брегга при реконструкции голограммы выполняются не только для луча r₁o , но и для любых лучей, совпадающих с образующими дифракционного конуса. Если протяжённый "читающий" источник обеспечивает направления "читающих" лучей в участке конической поверхности,ограниченной, например, лучами bо и со, то восстановленное изображение линии В_i, a_i, С_i будет соответствовать дуге c'a_ib'. Поэтому, если запись трёхмерной голограмvы была проведена точечныv опорным источником, реконструкция протяжённым источником приведёт к размытию каждой точки изображения в линию и тем самым к значительному размытию изображения предмета. Таким образом, в этом случае реконструкцию следует вести точечным источником (как и при реконструкции плоских голограмм). Это существенное ограничение может быть снято, если записывающий источник представляет собой некоторую

непрерывную совокупность светящихся точек. Поясним это на примере, изображённом на рис.7б, где запись предмета производилась опорным источником, состоящим из двух точек. Конуса, соответствующие дифракции под углами Θ₁, и o₂, имеют одну

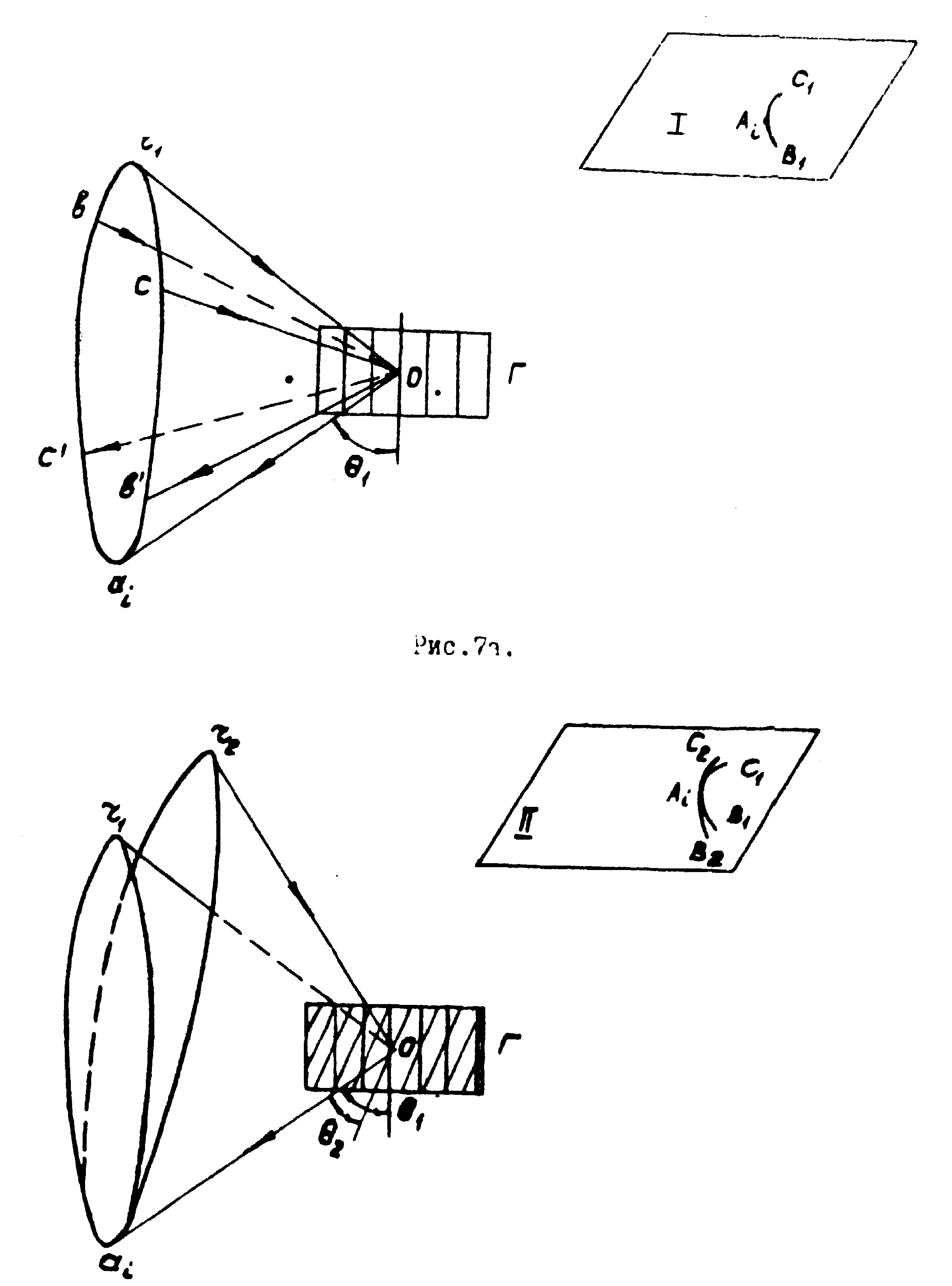
Рис.76.

общую образующую Оa_i. Поэтому при реконструкции голограммы про-тяжённым источником восстановленное изображение будет содержать две дуги С₁В₁ и c₂В₂, которые пересекутся в точке А_i, если "читающий" источник будет обеспечивать направления лучей r₁o и r₂o . При увеличении числа записывающих точек будет возрастать и число дифракционных конусов, объединённых одной общей образующей Оa_i. Поэтому точка a_i будет являться точкой пересечения многих линий типа С₁В₁ и её изображение может стать достаточно контрастным.

В завершение лекции заметим, что при анализе процессов записи и "чтения" трёхмерных голограмм не использовалось понятие опорного луча. Это не является случайным, если учесть отмеченную выше высокую избирательность трёхмерных голограмм по отношению к процессу реконструкции. При использовании объёмных светочувствительных элементов каждая точка предмета может рассматриваться как опорная, записывающая по отношению к остальным точкам. Отказ от необходимости использования специально выделенного в пространстве (по углу) опорного луча при записи является ещё одним важным свойством трёхмерных голограмм.

Л и т е р а т у р а

1. В.В.Аристов, В.Л.Броуде, В.Л .Ковальский, В.К.Полянский,

В.Б.Тимофеев, В.Ш.Шехтман. ДАН СССР, 1, 177 (1967).

2. Ю.Н.Денисюк. ДАН СССР, 144, 6 (1962).

3. В.В.Аристов, В.Г.Лысенко, В.Б.Тимофеев, В.Ш.Шехтман.