|
|
 |
 |

|
| |
ЯВЛЕНИЕ САМОРЕПРОДУКЦИИ И ВОССТАНОВЛЕНИЕ УЛЬТРАЗВУКОВЫХ
ГОЛОГРАММ НЕПЛОСКОЙ ФОРМЫ, ПОЛУЧЕННЫХ МЕТОДОМ ЛЕВИТАЦИИ
А.М.Андреев, А.Р.Ванян, В.М.Гинзбург, Н.М.Рамишвили
Описан метод устранения искажений восстановленных изображений с УЗ голограмм, полученных методом левитации, при наличии деформации поверхности голограммы из-за звукового радиационного давления. В основу метода положено предположение о том, что известно математическое описание формы поверхности голограммы. Предлагается использовать эффект Тальбота для определения формы деформирующейся поверхности раздела жидкость-газ под воздействием произвольной силы. Приведены экспериментальные результаты.
Методы ультразвуковой (УЗ) голографии до последнего времени не нашли широкого применения из-за ряда трудностей, свойственных способам получения и восстановления голограмм. Эти трудности особенно велики при голографировании динамических объектов и процессов. Кроме этого, при оптическом восстановлении звуковых голограмм во многих случаях теряется смысл использования голографических принципов, так как желаемая информация о трехмерности реконструированного изображения теряется из-за большого различия длин оптического и УЗВ диапазона (~10 3). Подробный обзор способов получения звуковых изображений методами акустической голографии и пути их развития широко освещены в литературе /1,2/. Отметим, что в настоящее время среди существующих методов предпочтение дается тем, которые предполагают преобразование энергии звуковых колебаний в электрический сигнал, а затем его визуализацию на дисплее: хотя, по мнению Грегуша /2/, было бы неправильно думать, что методы с использованием
- 126 -
непрерывных пространственных детекторов, позволяющих непосредственно преобразовывать акустическое изображение в оптическое, не будут иметь будущего. Одним из первоначальных методов акустической голографии является метод левитации поверхности жидкости, впервые предложенный С.Я.Соколовым в 30х годах /3/, который фактически первым сделал акустическую голограмму Габоровского типа еще до изобретения Габором оптической голографии. Применительно к ультразвуковой голографической схеме с внеосевым опорным пучком этот метод впервые использован Р.К.Мюллером /4/. Однако, в своем первоначальном виде схема Мюллера не нашла практического применения главным образом из-за свойственного ей основного недостатка - сильных аберрационных искажений восстановленных изображений. Эти искажения связаны с тем, что при работе в непрерывном режиме излучения ультразвуковой волны, помимо поверхностного рельефа, обусловленного интерференцией, возникает подъем поверхности в целом, вызванный радиационным давлением ультразвука /5/. При работе на частотах около 3 МГц амплитуды ультразвуковых волн на поверхности имеют 100-1000a, что существенно меньше длины облучающей световой волны. Однако, подъем поверхности, вызванный радиационным давлением ("горб"), для используемых в практике уровней мощностей, обычно, намного больше световой волны. Так как форма поверхности жидкости (голограмма) отличается от плоской (или сферической), в восстановленном изображении возникают искажения. Как отмечено в работе /6/, если ввести аберрационную функцию w(х,у), являющуюся мерой отклонения формы поверхности от сферы, то дополнительный сдвиг фазы отраженного света соответствует члену ехр(i4p
/λl) , где λl -длина волны света. Поэтому вместо идеального изображения, описываемого некоторой функцией ƒs(x,у) получается размытое изображение :
ƒ's=ƒs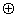 exp(i4p exp(i4p
w/λl) (1)
Существуют методы устранения этих искажений. haпример, использование миникюветы с вязкой жидкостью, связанной акустически
- 127 -
тонкой мембраной с основным водным бассейном. В этом случае радиационное давление из-за малого поверхностного натяжения жидкости в миникювете приводит только к незначительному подъему жидкости, не вносящему искажений при восстановлении голограммы. Однако, для получения качественных изображений в такой установке необходимо выполнить еще ряд условий. В результате теоретического анализа погрешностей А.В.Кларк в работе /7/ показал, что помимо погрешностей, вносимых подъемом поверхности из-за радиационного давления, существенные погрешности могут вносить собственные колебания мембраны миникюветы. Кроме того, должен быть удовлетворен ряд требований к конструкции установки, к подбору жидкостей в миникювете и др. Трудности, связанные с необходимостью удовлетворения этих требований, по-видимому, привели к тому, что дальнейшие исследования в области ультразвуковой голографии проводились, в основном, с использованием импульсных источников ультразвука и света, как в аналоговом варианте, так и в сочетании с быстрым сканированием поверхности УЗ голограммы лазерным лучом, электронным лучом (с помощью трубки Соколова) и др.
Целью настоящей работы является описание результатов исследований, выполненных для "реабилитации" простейшей и в то же время более информативной безлинзовой схемы УЗ голографии, предложенной Мюллером в варианте, изображенном на рис.1. В основу предлагаемого метода "реабилитации" положено предположение, что известно математическое описание формы поверхности голограммы, деформированной радиационным давлением ультразвука. Тогда, использование выражения (1), либо непосредственное восстановление на ЭВМ УЗ голограммы, имеющей известную форму поверхности, позволяют получать неискаженное изображение объекта. Существующие в настоящее время устройства ввода оптической информации в ЭВМ и применений быстродействующих мини-ЭВМ позволяют наблюдать эти изображения на мониторе в реальном времени. Определение формы поверхности голограммы можно производить описанным в работе /8/ методом, по оптическому изображению периодической решетки в плоскости первой саморепродукции (эффект Тальбота). На пути формирования этого изображения происходит отражение
- 128 -
света от возмущенной поверхности, приводящее к искажению изображения решетки в плоскости регистрации. Если поверхность голограммы имеет произвольную неплоскую форму, то можно выделить два случая. Первый - поверхность голограммы имеет осесимметричную форму (с произвольным центральным сечением). Такие голограммы образуются на поверхности раздела вода-воздух в том случае, если интенсивность опорной волны (которая создает осесимметричный горб на поверхности воды) намного превосходит интенсивность предметной волны, или когда объект является фазовым и форма горба практически не искажается полем объекта. В таком случае в качестве решетки для саморепродукции достаточно использовать одномерную решетку из параллельных полос. Так как в данном случае необходимо одновременно получать информацию и о форме поверхности голограммы, и о существующих на ней интерференционных полосах, то линии одномерной решетки ориентируются ортогонально к голографическим полосам.
На рис.2 приведено изображение акустической голограммы трех щелей, вырезанных в резине. Длина и ширина каждой щели, соответственно, равны 28 λ и 36λ. На том же изображении видны ортогонально направленные линии одномерной решетки, по которым рассчитан профиль поверхности голограммы, изображенный на рис.3. Расчет координат интерференционных линий на голограмме (Хh,y h) по координатам (х,у) этих линий в плоскости саморепродукции производится по формулам:
xh=x[1-s
(r)/(x2+y2)½],
yh=y[1-s
(r)/(x2+y2)½],
где s
(r) - смещение полос одномерной решетки в плоскости саморепродукции вследствие отражения света от возмущенной поверхности голограммы.
Координаты z(Хh,y h) определяются интерполяцией по кривой z(r). Влияние деформации поверхности голограммы при ее оптическом восстановлении приводит к полному размытию изображения. Однако, при машинном восстановлении голограммы
- 129 -
можно принять z(Хh,y h) »
0 , так как даже максимальная высота, горба (рис.3) мала по сравнению с длиной звуковой волны. После восстановления на ЭВМ (с помощью интеграла Кирхгофа-Френеля) изображение щелей с голограммы, распечатанное на расстоянии z = 130 мм по массиву (Хh,y h) из 50х50 точек, показано на рис.4. Как видно из этого рисунка, разрешение между щелями составляет ~ 5λ, что примерно соответствует теоретическому значению d
»
1.22zλ/2r0 »
3,2λ для голограммы, имеющей размер 2r0 = 35,7λ. Искажение изображения, по-видимому, обусловлено частичной асимметрией поверхности голограммы, вызванной затуханием, вносимым объектом (вследствие отличия его от чисто фазового), а также аберрациями оптического коллиматора. Для исключения этих искажений, т.е. для восстановления акустических голограмм произвольных объектов (не прибегая к подавлению горба пленками), необходимо использовать саморепродукцию двумерных решеток, что дает возможность определения формы существенно несимметричных поверхностей, возмущенных под воздействием произвольных факторов (ветра, течения и т.д.).
Отметим, что информация в ЭВМ вводилась бинарным способом, т.е. вводились данные только о координатах интерференционных полос на голограмме, предполагая, что интенсивность отраженного поля вдоль этих полос одинакова. Однако, при таком квантовании вводимой информации интервалы дискретизации не являются эквидистантными, что не позволяет применять алгоритм БПФ. Иной способ ввода информации в ЭВМ заключается во введении дискретной информации не о координатах вдоль интерференционных полос, а о величине отражательной (или пропускательной) способности голограммы, как обычно фотометрируя ее изображение, полученное в плоскости саморепродукции.
При этом в массив данных следует вносить информацию, полученную в таких неэквидистантных точках изображения плоскости саморепродукции, которые соответствуют эвидистантным точкам исходной решетки на голограмме (т.е. на поверхности воды). Такая выборка фактически является способом учета формы поверхности, позволяющим применять БПФ, .которое имеет бесспорные преимущества
- 150 -
в смысле сокращения требуемого машинного времени.
Для восстановления УЗ голограмм динамических объектов можно использовать киносъемку с последующей покадровой обработкой по описанному методу.
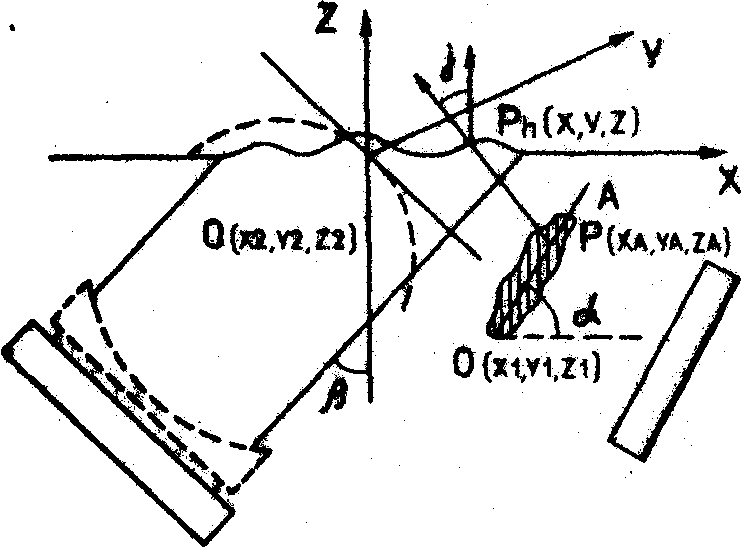
Рис.1. Схема УЗВ голографии Мюллера.

Рис.2. Изображение голограммы трех щелей в плоскости саморепродукции одномерной решетки.
- 131 -
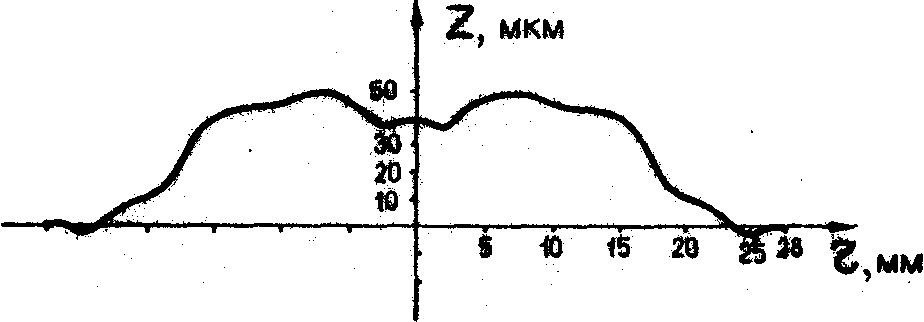
Рис.3. Центральное сечение поверхности голограммы, изображенной на Рис.2.

Рис.4. Мнимое изображение, восстановленное с голограммы, представлено на рис.2. 1 - уровень (0-5)дБ, 2 - (5-10) дБ, 3 - (10-15) дБ, 4 - более 15дБ.
- 132 -
Л и т е р а т у р а
1. В.Д.Свет. Методы акустической голографии. Л.: ЦНИИ. "Румб". 1976.
2. П.Грегуш. Звуковедение. М.: Мир. 1982.
3. С.Я.Соколов. Патент США №2164125. Приоритет - август 1937, 21: июнь 1939, 27.
4. mueller r.k. and sheridon n.k. sound holograms and optical reconstruction. appl. phys. lett., 1966, v.9, p.328.
5. boa-teh chu and apfel b.e. acoustic radiation pressure produced by a beam of sound. tos А, 1982, v.72, n.6, pp.1673-1687.
6. Р.К.Мюллер. Акустическая голография. // Применение голографии. Под ред. Гудмена Дж. Пер. с англ. – М.: Мир. 1973.
7. v.alfred, tr.clark. on obtaining maximum performance from liquid surface leritation holography. acaustical imaginge, v.8. mew york and london, plenum Ргеss, 1978, pp.417-453.
8. А.М.Андреев, А.Р.Ванян, Н.М.Рамишвили. Применение явления саморепродукции для измерения формы поверхности жидкости, возмущенной радиационным давлением ультразвука. Радиотехника и электроника. 1935. Т.30. №1О. С.2057-2058.
- 133 -
УДК 535
ЯВЛЕНИЕ САМОРЕПРОДУКЦИИ И ИЗМЕРЕНИЕ УЛЬТРАЗВУКОВЫХ ПОЛЕЙ
ПЕРВИЧНЫХ И ВТОРИЧНЫХ ИЗЛУЧАТЕЛЕЙ В БЛИЖНЕЙ ЗОНЕ
А.М.Андреев, Д.А.Болквадзе, А.Р.Ванян,
В.М.Гинзбург, Н.М.Рамишвили
Описана возможность расчета ближнего поля (как статистического, так и изменяющегося во времени) ультразвукового излучателя произвольной конфигурации с использованием эффекта Тальбота и метода поверхностного рельефа. Приведены экспериментальные результаты.
Как известно, в зоне Френеля* характеристика направленности звуковых антенн r зависит не только от углов Q
и j
(в сферической системе координат), но и от расстояния r до точки наблюдения, и, в общем случае, не всегда поддается расчету. Существуют приближенные формулы для определения распределения звукового поля в ближней зоне. Например, для круглого поршневого излучателя, закрепленного в жестком экране, в предположении, что ближнее поле является коллимированным пучком, состоящим из однородных, плоских бегущих волн (что строго говоря не соответствует действительности), в работе /1/ получено выражение для распределения звукового давления Р, которое имеет вид:
Р=2r
cusin÷
1/2К[(r2+d2/4)½-r]÷
,
где u - скорость движения поршня, c -скорость звуковой волны, r
- плотность жидкости. Для определения структуры ближнего поля в работе /2/ использован принцип Гюйгенса. Предполагается,
* - границей зоны Френеля принято считать расстояние r, удовлетворяющее условию: r»
d2/4λ, где λ - длина волны, d - поперечные размеры излучателя.
- 134 -
что интерференционная картина в ближнем поле круглого излучателя образуется из плоской волны, генерированной от плоскости излучателя, и краевой волны, генерированной от периметра излучателя. Как отмечено в этой работе, результаты расчета по такой многоволновой модели хорошо соответствуют экспериментальным данным. Такой же метод реализован и для квадратного излучателя. Для излучателей более сложной формы расчет поля в ближней зоне гораздо труднее. Однако, необходимость определения характеристик звукового поля излучателей произвольной формы возникает как в теоретических задачах гидроакустики, так и для многих практических применений. Например, в акустической голографии зона Френеля используется непосредственно, так как только в ней можно получать необходимое разрешение. Необходимость в измерении распределения поля в ближней зоне возникает также для определения параметров излучающих антенн в дальней зоне, когда непосредственные измерения в лабораторных условиях невыполнимы.
Наиболее часто применяемый в настоящее время способ измерения распределения поля методом механического сканирования накладывает жесткие требования на размеры звуковых приемников, что вызывает большие трудности в ультразвуковой области. Это особенно важно в ближней зоне, где градиент давления звукового поля весьма ощутим. Если требования к размерам приемников не выполняются, то поле может быть искажено рассеянием на приемнике и, кроме того, поле усредняется по поверхности приемника. Отметим также, что такой способ измерения приемлем только для статических полей. Методы электронного сканирования, применяемые в звуковизорах (Уникон), ограничены использованием приемников, апертура которых не превышает ~ 5 см. По-видимому, наиболее удобным следует считать метод поверхностного рельефа. Как известно, статический рельеф на поверхности жидкости устанавливается при "равновесии" сил радиационного давления ультразвука, поверхностного натяжения и гравитации. Существующие методы измерения радиационного давления радиометром (для всех его разновидностей предполагают использование в качестве приемного элемента диска, шарика или конуса, размеры которых много больше
- 135 -
длины ультразвуковой волны. Поэтому, количественное определение распределения поля ультразвуковой волны по его визуализированному, методом поверхностного рельефа, изображению предлагается производить по форме деформированной радиационным давлением поверхности раздела жидкость-газ. Форму деформированной поверхности h(х,у), как статическую, так и изменяющуюся во времени, можно определять, используя эффект Тальбота, по методу, описанному в работе /3/. Таким образом, если в качестве регистрирующей приемной среды использовать поверхность раздела жидкость-газ, деформацию которой (из-за радиационного давления звуковой волны) можно измерить, то по известной форме поверхности можно рассчитать распределение поля, возбуждаемое излучателем, установленным на расстоянии от поверхности жидкости, соответствующем ближней зоне. Как показано в работе /4/, величина деформации поверхности жидкости h(х,у), измеряемая вдоль нормали к невозмущенной поверхности, связана с интенсивностью падающей волны следующим образом: h~i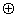 К, где i - интенсивность звуковой волны, К - импульсный отклик поверхности жидкости. Выполнив фурье-преобразование, из последнего уравнения получим: f[h]~f[i]·f[К], где f[К] - является модуляционной передаточной функцией поверхности жидкости и равна /4/: f[k]= 1/(1+g
2u
2), где К, где i - интенсивность звуковой волны, К - импульсный отклик поверхности жидкости. Выполнив фурье-преобразование, из последнего уравнения получим: f[h]~f[i]·f[К], где f[К] - является модуляционной передаточной функцией поверхности жидкости и равна /4/: f[k]= 1/(1+g
2u
2), где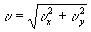 -пространственная частота, g
- характеристическая длина, зависящая от поверхностного натяжения s
и плотности r
: -пространственная частота, g
- характеристическая длина, зависящая от поверхностного натяжения s
и плотности r
: 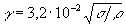 (см). Для границы раздела вода-воздух g
»
2 мм. Тогда: f[i]~f[h]·(1+g
2u
2). Проведя обратное фурье-преобразование, из последнего уравнения получим распределение интенсивности i(х,у) по поверхности жидкости. Радиационное давление pr на идеальный отражатель (поверхность раздела жидкость-газ) в случае нормального падения звуковой волны, имеющей интенсивность i, среднеквадратичное значение звукового давления Р, скорость С в жидкости с плотностью r
, равно: pr = 2i/c = 3p2/r
c2. Следовательно, по известному значению i можно рассчитать распределение вдоль поверхности воды как радиационного Рr, так и звукового (см). Для границы раздела вода-воздух g
»
2 мм. Тогда: f[i]~f[h]·(1+g
2u
2). Проведя обратное фурье-преобразование, из последнего уравнения получим распределение интенсивности i(х,у) по поверхности жидкости. Радиационное давление pr на идеальный отражатель (поверхность раздела жидкость-газ) в случае нормального падения звуковой волны, имеющей интенсивность i, среднеквадратичное значение звукового давления Р, скорость С в жидкости с плотностью r
, равно: pr = 2i/c = 3p2/r
c2. Следовательно, по известному значению i можно рассчитать распределение вдоль поверхности воды как радиационного Рr, так и звукового
- 136 -
давления Р, в зависимости от высоты вспученной поверхности h(х,у). Пользуясь хорошо разработанными методами /5/, полученные распределения Рr и Р в ближней зоне облучателя позволяют решить обратную задачу - определение поля в раскрыве облучателя, а затем при необходимости и поле в дальней зоне.
Для иллюстрации описанного метода было рассчитано распределение интенсивности плоской ультразвуковой волны, дифрагирующей на препятствии в виде крестика. Распределение рассчитывалось в зоне Френеля на расстоянии 98 мм от крестика, изготовленного из резиновых полосок длиной 55,8 λ и шириной 8,4λ. Частота ультразвуковой волны 4,18 мГц. Форма деформированной поверхности раздела h(х,у) вычислялась по методу, описанному в /3/. Для расчета использовалась ЭВМ ЕС-1О-55М и программы БПФ и обратного БПФ на алгоритмическом языке ФОРТРАН. На рис. приведено выведенное на графопостроителе изображение распределения интенсивности поля на поверхности раздела вода-воздух, выраженнoe в Вт/м2. Из рисунка видно, что интенсивность наблюдаемого поля имеет пиковое значение 1,64х104 Вт/м2, что соответствует радиационному давлению 21,87 Па. В провалах величина Рr уменьшается до значения 16,93 Па.
- 137 -
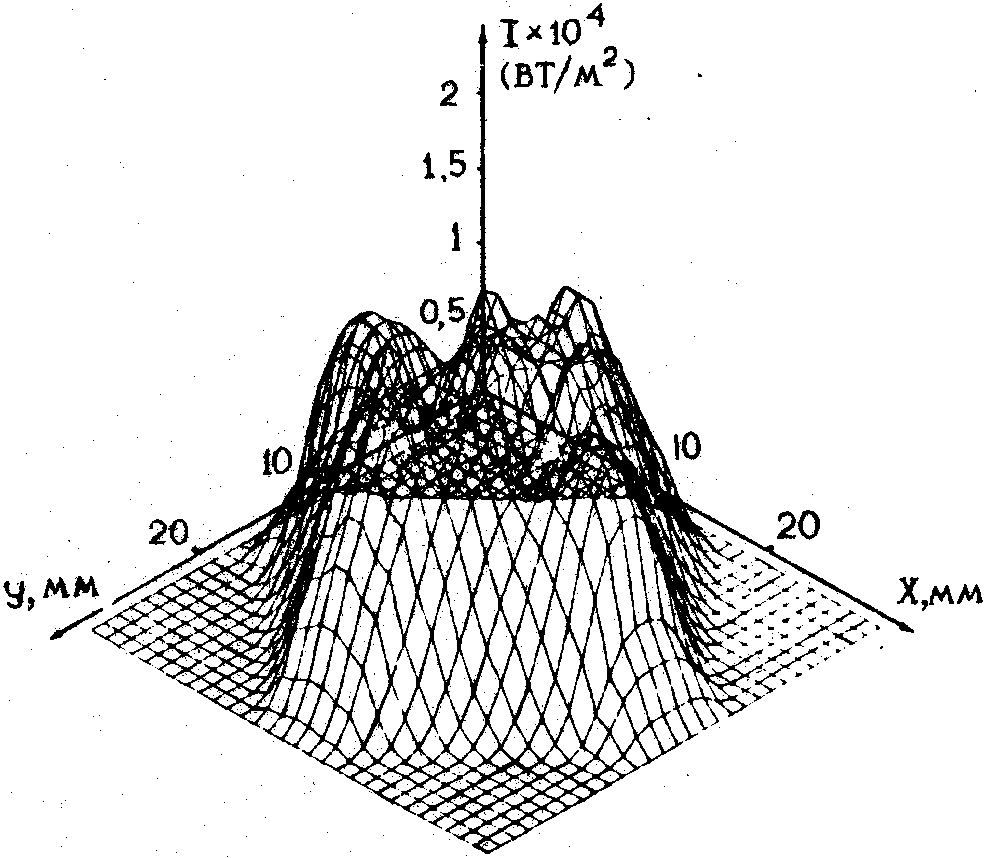
Рис. Распределение интенсивности в ближней зоне дифракции плоеной ультразвуковой волны на резиновом крестике.
- 138 –
Л и т е р а т у р а
1. Р.Боббер. Радиоакустические измерения. М.: Мир. 1974.
2. М.В.Фельдман, Ю.К.Энгельбрехт. О расчете ближнего поля ультразвукового излучателя // Акуст. журн. 1987. Т.33. № 2. c.367-369.
3. А.М.Андреев, В.М.Гинзбург, Ю.П.Пресняков, Н.М.Рамишвили. Использование явления саморепродукции для измерения формы возмущенной поверхности раздела жидкость-газ в динамике // Акуст. журн. 1987. Т.33. №1. c.93-96.
4. Р.К.Мюллер. Акустическая голография. // Применение голографии. Под ред. Гудмена Дж. Пер. с англ.- М.: Мир. 1973.
5. garret g.s. nare, t.tjotta, s.tjotta. nearfield of a large acoustical transducer // tasa. 1984, v.75, n 3, pp.769-779.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

