ЭФФЕКТ ВЕТВЛЕНИЯ ИНТЕРФЕРЕНЕЦИОННЫХ ПОЛОС ПРИ
СУПЕРПОЗИЦИИ ИДЕНТИЧНЫХ СПЕКЛ-ПОЛЕЙ
Б.Б.Горбатенко, И.С.Клименко, В.П.Рябухо. И.Р.Сатаев,
Б.В.Федулеев
Проведено теоретическое и экспериментальное рассмотрение эффекта ветвления полос в низкочастотной интерференционной картине, возникающей при суперпозиции идентичных спекл-полей. Показана связь точек ветвления с нулями амплитуды комплексной функции кросс-корреляции интерферирующих спекл-полей.
В работе /1/ было зарегистрировано наличие точек ветвления, то есть точек возникновения (уничтожения) интерференционных полос при суперпозиции идентичных спекл-полей. Аналогичный эффект наблюдался в работах /2-3/ в высокочастотной интерференционной картине (модулирующей спеклы), возникающей при суперпозиции спекл-поля и плоской опорной волны. В этом случае путем непосредственного вычисления распределения интенсивности в интерференционной картине было показано, что точки ветвления возникают в нулях комплексной амплитуды спекл-поля. Очевидно, однако, что нули комплексной амплитуды интерферирующих спекл-полей не могут быть причиной появления точек ветвления низкочастотной интерференционной картины, так как количество нулей комплексной амплитуды спекл-полей по порядку величины совпадает с количеством спеклов, и, кроме того, период низкочастотных полос на 2-3 порядка превышает размер спеклов.
Поведение полос в высокочастотной картине описывается интерференционным членом
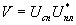(1)
где
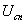и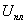
- комплексным амплитуды спекл-поля и поля плоской волны. Функция обращается в нуль в точках, где
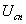= 0. В случае низкочастотной интерференционной картины эта функция v (в
- 43 -
дальнейшем функция видности) записывается в виде
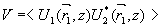(2)
где u1 и u2 - комплексные амплитуды интерферирующих полей в точке наблюдения, а скобки означают усреднение по ансамблю. Предположим, что функция v обращается в нуль в точке (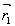
= 0, z = 0). Для того, чтобы исследовать поведение видности в окрестности нуля, рассмотрим функция кросс-корреляции.
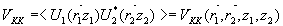(3)
связанную с видностыо очевидным соотношением
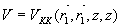(4)
Воспользовавшись тем, что функция (3) должна удовлетворять двум волновым уравнениям (по индексам переменных 1 и 2), можно показать, что при разложении в ряд функции (3) и учета соотношения (4), функция видности в малой окрестности нуля описывается выражением
v=a1x1+a2y1 (5)
где (x1,y1)= 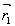, А1 и А2 - комплексные константы. Более того, как показано в /2/, решение вида (5) является в определенном смысле устойчивым по отношению к малым возмущениям.
Функция вида (5) обладает еще одним важным свойством: при обходе вокруг точки (0,0), в плоскости (x1,y1) она приобретает дополнительный набег фазы ±2p
. Поскольку интерференционная полоса есть сечение плоскостью наблюдения поверхности равной фазы, то это означает рождение или уничтожение в точке (0,0) интерференционной полосы.
Таким образом, точкам ветвления соответствуют нули функции видности. Отметим, что и появлению точек ветвления в высокочастотной интерференционной картине соответствует обращение в нуль функции (1).
Рассмотрим в качестве примера световое поле, восстановленное в плоскости (x0,y0), двукратно экспонированной френелевской
- 44 -
голограммой диффузно рассеивающего объекта с комплексным коэффициентом разложения t(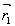), который в промежутке между экспозициями был поступательно смещен в собственной плоскости. Пусть это поле переотображается в плоскость наблюдения (x1,y1) (рис.1) тонкой положительной линзой с функцией пропускания зрачка.
Выразим поле в плоскости наблюдения с помощью интеграла Кирхгофа при условии коллимированного освещения объекта:
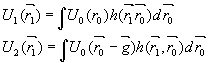(6)
где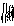
- вектор смещения объекта, h
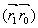- переходная функция оптической системы.
Используя для функции h приближение Френеля /4/, можно получить, подставив (6) в (2), выражение для видности:
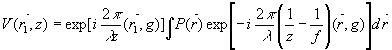(7)
Для круговой апертуры
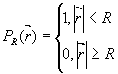(8)
получим
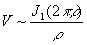(9)
где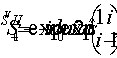
,a j1 - функция Бесселя первого порядка.
Видность, в соответствии с (9), обращается в нуль при значениях 2p
r
, равных корням функции Бесселя, причем сразу по всей плоскости z=const. Можно показать, однако, что при небольшом возмущении, добавленном к выражению, полученному в
- 45 -
Френелевском приближении, произойдет возврат к решению вида (5), то есть к изолированным в плоскости z=const нулям комплексной функции видности. В качестве такого возмущенного выражения можно рассматривать следующий порядок приближения интеграла Кирхгофа (6). Для получения такого приближения мы использовали метод стационарной фазы. Опуская выкладки, приведем основные результаты, подтверждаемые экспериментом. В целях упрощения анализа без ограничения общности будем считать, что сдвиг объекта происходит вдоль оси x.
В случае круговой апертуры (8) в результате расчетов получилось семейство линий нулевой видности, изображенное на рис.2 сплошной линией. Таким образом, в плоскости наблюдения z=const должны наблюдаться две точки ветвления противоположного знака вследствие того, что они принадлежат одной линии нулей /2/. Эти линии нулей лежат на семействе, поверхностей минимальной видности. Значения видности на этих поверхностях очень близки к нулю (~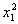
/ƒ2), хотя обращаются точно в нуль лишь на линиях , получающихся в сечении х=о. В сечении плоскости z=const этих поверхностей наблюдаются кривые, которые имеют вид эллипса с отношением полуосей а/b=
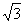. Семейство поверхностей минимальной видности получается в результате возмущения семейства плоскостей нулевой видности, существование которого следует из Френелевского приближения (9).
Получающаяся в результате плоскости наблюдения интерференционная картина приведена на рис.3. Хотя точек ветвления всего две, что подтверждается тем, что внутри эллипса ровно на одну полосу больше, чем снаружи, все полосы испытывают сбой фазы по границе эллипса. Причину этого сбоя иллюстрирует рис.4. Так как функция вида (5) линейно отображает окрестность точки (0,0), в плоскости (х1,у1) в комплексную плоскость (rev,jmv], то, если мы будем двигаться вдоль полосы в плоскость (х1,у1), то есть вдоль прямой х= const, фаза видности испытывает скачок, близкий к p
при прохождении вблизи нуля. Таким образом наличие у нуля видности достаточно большой окрестности, в которой она близка к нулю, приводит к делокализации точки ветвления полос.
- 46 -
В случае кольцевой апертуры
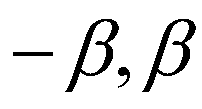
также существует семейство линий нулевой видности, аналогичное рис.2, однако, видность близка к нулю лишь в малой окрестности линии, принадлежащей к этому семейству. Вследствие этого точки ветвления в сечении z=const четко локализованы, что иллюстрирует рис.5. Общая картина выглядит следующим образом: в сечении интерференционной картины плоскостью z=const по мере удаления из фокальной плоскости появляется сначала пятно нулевой видности, а затем из него возникают две точки ветвления противоположного знака и разбегаются вдоль оси У.
Таким образом, характер ветвления интерференционных полос при суперпозиции идентичных спекл-полей существенным образом зависит от выбора апертуры наблюдательной системы. Установленная выше связь между нулями амплитуды комплексной функции видности и токами ветвления позволяет путем вычисления функции видности определять положение точек ветвления и степень их локализации.
Отметим также, что эффект ветвления низкочастотных интерференционных полос наблюдается при осуществлении суперпозиции идентичных спекл-полей методом спекл-интерферометрии, а также использовании на этапе наблюдения теплового восстанавливающего источника.
Л и т е р а т у р_а
1. И.С.Клименко, В.П.Рябухо, Б.В.Федулеев, Эффект "ветвления" интерференционных полос при суперпозиции идентичных спекл-полей. ЖТФ. 1985. Т.55. №5. С. 980-983.
2. Н.Б.Баранова, Б.Я.Зельдович. Дислокация поверхностей волнового фронта и нули амплитуды . ЖЭТФ. 1981. Т.80. №5. С.1789-1797.
3. Н.Б.Баранова, Б.Я.Зельдович, А.А.Мамаев и др. Исследование плотности дислокации волнового фронта световых полей со спекл-структурой. ЖЭТФ. 1982. Т.83. №5. c.i702-i7io.
4. Дж.Гудмен. Введение в фурье-оптику. М., "Мир". 1970. c.127.
- 47 -
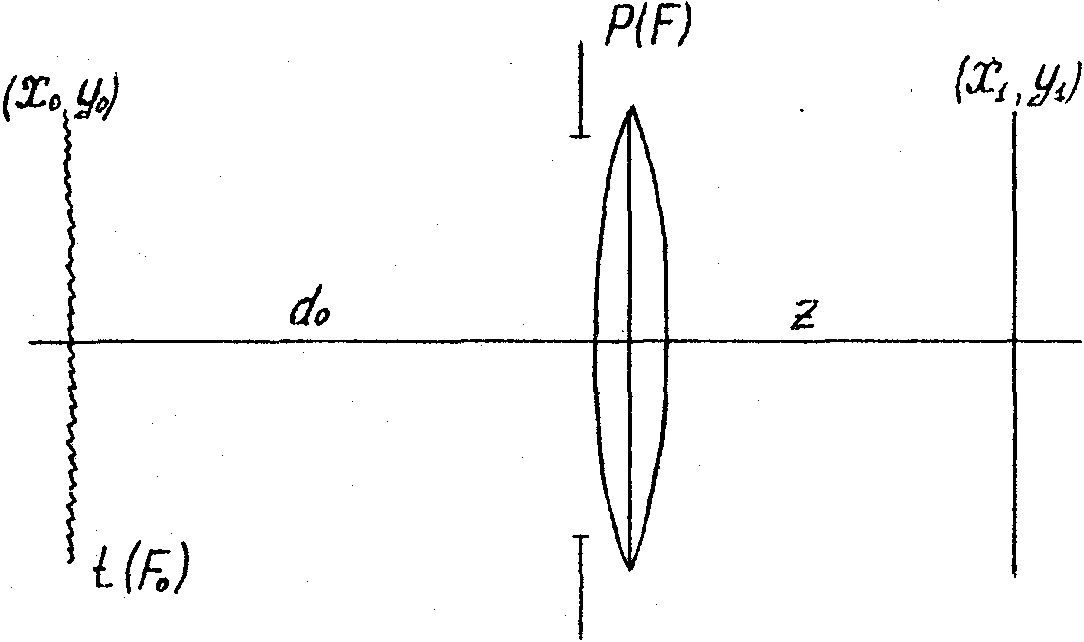
Рис.1. Схема наблюдения эффекта ветвления интерференционных полос.
Рис.2. Семейство линий нулевой видности для круговой апертуры наблюдательной системы (теоретический расчет).
- 48 -
Рис.3. Сбой фазы полос и эффект ветвления полос, происходящие на эллипсе минимальной видности. Экспериментальный результат регистрации интерференционной картины наблюдательной системой с круговой апертурой.
- 49 -
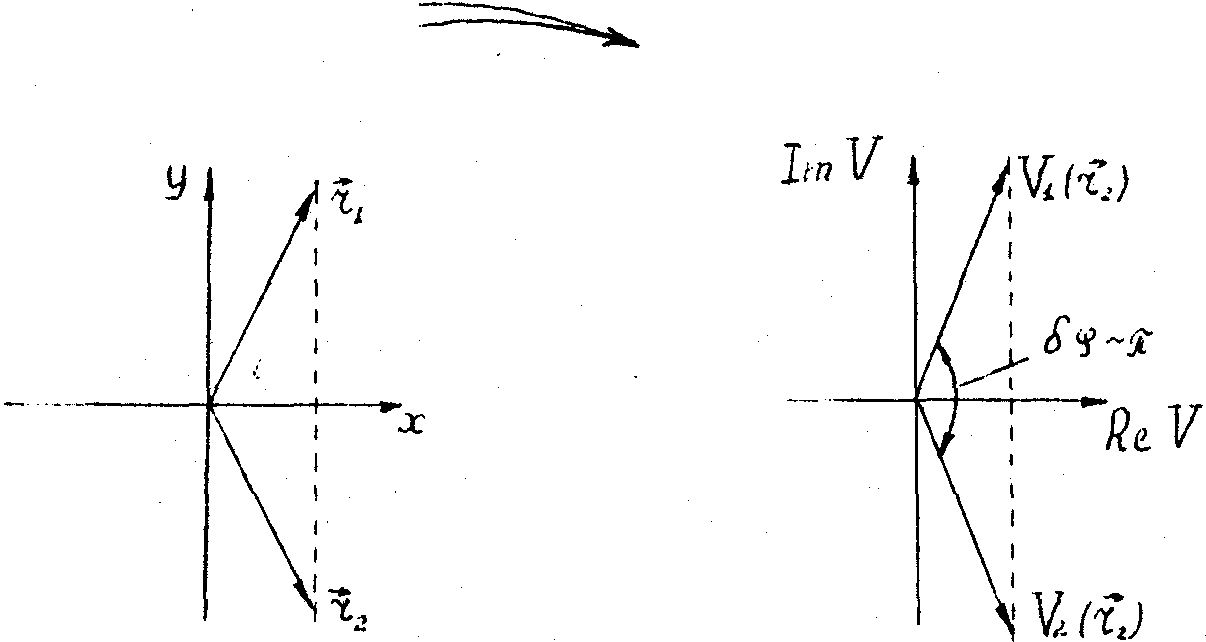
Рис.4. К вопросу о сбое фазы интерференционных полос в окрестности минимальных значений видности.
Рис.5. Локализация области ветвления интерференционных полос, регистрируемых в экспериментах с использованием наблюдательной системы с кольцевой апертурой.
