|
|
 |
 |

|
| |
ТЕНЕВОЕ ОПТИЧЕСКОЕ ЭХО
Т.Я.Дубнищева
Аналогия между явлением оптического эха и теневым эффектом была предложена и продемонстрирована В.П.Чеботаревым осенью 1986-го года на 8-ом советско-западногерманском семинаре по лазерной спектроскопии в Майнце. Когерентные отклики в газе типа оптического эха, когерентного излучения в разнесенных полях и в атомной интерферометрии оказались связаны со скачком фазы дипольного момента /1,2/. В настоящем сообщении дается простая геометрическая интерпретация формирования такого скачка и указывается ряд приложений.
Поясним, как образуется такой скачок фазы. Рассмотрим газ в поле двух, распространяющихся вдоль оси z импульсов стоячей волны ( Е1 и Е2 - амплитуда импульсов, w
- частота поля, t
- длительность импульсов, Т - промежуток между импульсами, причем t
<Т):
Е( z,t)=2[e1ƒ1(t)+e2ƒ2(t-t)]coskzexp(-iw
t)+k.c. (1)
Для нахождения дипольного момента в точке z, t решаются уравнения Шредингера для амплитуд вероятности нижнего а и верхнего b уровней:
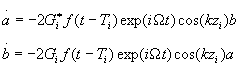 (2) (2)
Здесь – zi=z-v(t-ti) - координата атома в момент взаимодействия, v - проекция скорости атома на ось z, g(t)=g1¦
1(t)+g2¦
2(t-t), g=idbaei/ћ, t1=0, t 2=t, d ba - дипольный момент перехода, частоты w
ba, W
= w
- w
ba. Для амплитуд ai и bi после взаимодействия i-ым импульсом имеем (решая (2)
- 173 -
в линейном по g 1 и квадратичном по g2 приближении):
b1=2g1t
cosj
1; a1=1 (3)
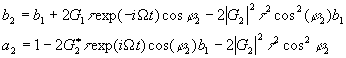 (4) (4)
После действия 1-го импульса из-за смещения атома вдоль оси фаза диполей плавно меняется во времени:
de(t)=dbaexp(-iw
bat)cos[k(z-vt)]2g1t
(5)
Превоначально сфазированные диполи расфазируются за время (кΔv)-1 где Δv - область скоростей атомов; это нарушит когерентность ансамбля. После 2-го импульса (t>t
+t) для нелинейной добавки к d(t) получим:
dne(t)=dba(-iw
t)2ï
g2ï
2 g1t
3{exp[iW
(t-2t)]+
+exp(iW
t)}{2cos[k(z-vt)]+cos[k(z-u(t-2t))]} (6)
Из сравнения фаз в выражениях (5) и (6) при t=Т видно, что под действием 2-го импульса также происходит скачкообразная инверсия фазы ~ (kvt). После усреднения по скоростям эти члены с "доплеровской" фазой обеспечивают появление когерентного отклика газа в t=2Т - так называемый сигнал эха. Выражение в фигурных скобках в формуле (6), являющееся аналогом "временной" фазы ~ (W
Т), состоит из двух слагаемых - содержащего и не содержащего инверсию фазы. После усреднения по скоростям из первого получается доплеровски уширенная подложка, а из второго - бездоплеровский резонанс - КИРП.
Рассмотрим теперь процессы, квадратичные по g1 и линейные по g2. Получаются выражения типа (3-6). Возникающему в этом случае скачку фазу соответствует локализация когерентного отклика в момент – Т, т.е. в прошлом. Это так называемое "мнимое" эхо /3/.
Квадраты амплитуд вероятности ï
а 2ï
2 и ï
b2ï
2 для процессов ~g1ï
g2ï
2:
- 174 -
ï
a2ï
2=[1-2ï
g2ï
2t
2cos2j
2]+(2t
cosj
2)2(g2*eiW
tb1)2-
-(2t
cosj
2)[1-2ï
g2ï
2t
2cos2j
2][g2*eiW
tb1+g2e-iW
tb1*] (7a)
ï
b2ï
2=(b1-2ï
g2ï
2t
2cos2j
2·b1)2+4t
2cos2j
2(g2e-iW
t)2-
-(2t
cosj
2)[1-2ï
g2ï
2t
2cos2j
2]b1[g2e-iW
t+k.c.] (7б)
Отсюда видно, что волновая функция атома оказалась промодулирована полем второго импульса. И появление бездоплеровского резонанса – КИРП -, связанного с последними слагаемыми в формуле (4), есть следствие амплитудной модуляции.
Модуляция волновой функции ведет к модуляции макроскопических характеристик газа - заселенности уровней и поляризации среды. Известно, что в сильной стоячей волне в первоначально неполяризованном газе возникнут четные пространственные гармоники заселенностей уровней(с периодом λ/2m, где m - целое число) и нечетные гармоники поляризации с периодом λ/(2m+1)
Резонансная стоячая волна может служить эффективной дифракционной решеткой для нейтральных атомов. При рассеянии на стоячей волне из-за эффекта отдачи импульс атома меняется на величину ±ћk. При рассеянии на первой стоячей волне атомный пучок расщепляется на два когерентных пучка (в волновой функции возникают две компоненты Y
+ и Y
-, соответствующие изменению импульса атома). При последующем рассеянии на второй - эти пучки совмещаются, и в точке их пересечения возникнет интерференционная картина. (В квадрате модуля волновой функции возникнет периодическая структура, а фаза ее за время t меняется скачком на величину d
j
=kvt+Δt, где 1-ое слагаемое дает доплеровский сдвиг частоты, а 2-ое - квантовая добавка к фазе)/4/.
В оптическом диапазоне объектами атомной интерферометрии могут служить (ca, na,mg,pb...), и при температуре в пучке ~ 300 К дифракционный угол q
d~10 -4. В таких пучках угловая расходимость q
~10-2¸
10-3, поэтому пространственного
- 175 -
разделения не происходит. При условии q
>q
d о волновых свойствах частиц можно судить лишь по возникающей из-за интерференции периодической структуры в пространственном распределении плотности атомов, т.е. по гармоникам плотности с периодом ~ λ. Такие гармоники могут наблюдаться в условиях эха.
Для компенсации большой фазы j
d можно использовать стоячие волны, разнесенные на расстояние l. Здесь, по аналогии со скачком фазы дипольного момента, происходит скачок фазы волновой функции поступательного движения атома, который и компенсирует j
d, и на расстоянии l возникнет четкая интерференционная картина, состоящая из гармоник плотности.
Скачок фаз в нелинейном дипольном моменте можно представить как пространственную модуляцию дипольного момента частиц, возникающую из-за пространственной амплитудной модуляции дипольного момента d 1 во втором поле. Но такую модуляцию можно осуществить, используя вместо полей стоячей волны две решетки, разнесенные на расстояние l с периодами L
и L
/2. В геометрической оптике известно, что при наложении теней от двух таких решеток на расстоянии 2l возникнет периодическая структура. В протяженном пучке частиц с угловой расходимостью q
распространяющегося вдоль оси х, при 100% - модуляции пучка периодическая структура после 1-ой решетки с периодом L
быстро разрушается из-за перекрытия пучков, исходящих из отверстий решетки. После прохождения через 2-ую решетку с периодом L
/2 эта структура может быстро восстанавливаться в точке х=2l. Эта аналогия с теневым эффектом может оказаться полезной.
Рассмотрим, как возникают скачки фаз периодической структуры в пространственном распределении частиц. Пусть u и v - проекции скорости частиц на оси х и z. При свободном разлете функция распределения частиц по координатам и по углу q
=v/u меняется по закону (для простоты будем считать u=const):
¦
( z,x+Δx,q
)=¦
(z-q
Δx,x,q
) (12)
- 176 -
Если на пути пучка расположена тонкая решетка, то вблизи нее функция распределения меняется скачком
¦
+(z,x,q
)=λ(z)¦
-(z,x, q
) (13)
где λ(z) - пространственное распределение пропускания решетки, ¦
- и ¦
+ - функции распределения до и после прохождения решетки. Пусть решетка, расположенная при х=0, модулирует плотность по закону
λ 1(z)=a 0+a 1cos(kz) (14)
где k=2p
/λ, а решетка, расположенная при x=l, имеет вдвое меньший период
λ 2(z)=a 0+a 2cos(2kz) (15)
При x<l и считая, что xq
<<b, где b - размер пучка вдоль оси, из формул (12)-(13) получим:
¦
(x,z,q
)={a0+a1cos[k(z-q
x)]}¦
(z,0,q
) (16)
Видно, что при заданном q
узлы периодической структуры на расстоянии x сместятся на величину q
x, т.е. в периодической зависимости возникнет фазовая добавка
j
0=kq
x (17)
Ниже мы убедимся, что эта фаза ( 17) аналогична изменению фазы атомного диполя из-за доплеровското сдвига частоты.
Усреднение по углам приводит к тому, что в распределении плотности
¦
(z,x)= ∫dq
¦
(z,x,q
) (18)
периодическая структура сохраняется лишь на расстоянии х£
λ/q
. При больших х эта структура размывается.
Рассмотрим теперь действие второй решетки. При х> l
- 177 -
интересуемся добавкой к функции распределения вида ( 16):
d
¦
(z,q
,x)=a1,a2cos[k(z-q
x)]cos{2k[z-q
(x-l)]}¦
(z,0,q
)=
= ½a1a2[cos{k[z-q
(x-2l)]}+cos{k[3z-q
(3x-2l)]}] (19)
Первое слагаемое в квадратных скобках содержит по сравнению с периодической зависимостью (16) фазовый скачок – 2klq
, который приводит к инверсии фазы в точке x=l. Компенсация этого скачка за счет линейного по х роста фазы происходит в точке эха при x=2l. В этой точке локализуется четкая периодическая структура, d
¦
(z,2l)=(½)a1a2cos(kz), копирующая распределение, возникшее непосредственно сразу после первой решетки.
Оценим возможности наблюдения в пучке частиц, когда используется разрешенный переход в бесструктурных частицах. Нижний уровень является метастабильным, и фазовая память переносится атомами только в этом состоянии. Пусть ширина перехода между уровнями Г больше обратного времени взаимодействия с полями, создающими решетки, и доплеровской ширины линии в пучке Г >>t
-1, Г>>kv0q
. Эффективный гамильтониан двухквантового процесса возмущения нижнего метастабильного уровня (виртуально через верхний уровень) u=ï
deï
2/ћ2( W
+i Г) эрмитов при W
>>Г, а вблизи резонанса - неэрмитов. Впервые скалярное уравнение Шредингера с таким гамильтонианом рассматривалось в /5/. Поэтому вблизи резонанса не сохраняется вероятность нахождения частицы на нижнем уровне. Физически это связано с наличием неупругого процесса перехода с нижнего метастабильного на другие метастабильные термы через верхний уровень. Из соответствующих уравнений для матрицы плотности имеем:
r
+=exp{[-ï
deï
2/ ћГ]t
}r
-
Поскольку e=2cos(kz), Е2=2(1+соs(2кz)), то
λ(z)=exp{-2Y
(l+cos2kz)}, Y
=[ï
deï
2/ћ2Г]t
(20)
В этом случае решетки могут быть выражены через модифицированные функции Бесселя ij(х):
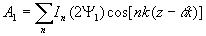 (14a) (14a)
- 178 -
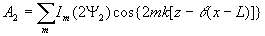
(14б)
Набег фаз связан с расходимостью q
. Подобно (16), получим:
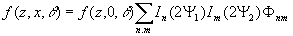
, (16а)
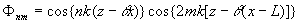
(16б)
Для пространственного распределения плотности получаем:
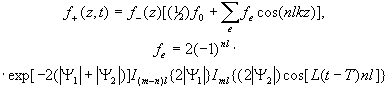
(16в)
Полученный результат совпадает с распределением плотности в интерференционной картине при интерференции атомов в сильном внешнем поле для случая чисто-амплитудного возмущения /4/.
Значения xq, при которых фазы будут скомпенсированы, найдем из условия: -(2p
q
/L
)[2m(xq-l)-nxq]=2p
q,
Отсюда xq=(2m-n)-1[2ml-qL
/q
] (21)
Для первых гармоник n=m=1 и q=0 имеем x0=2l. Сравнивая этот результат с формулой (19) и обсуждением ее для теневого эффекта, замечаем, что в точке 2 происходит компенсация набегов фаз. Выделим эту плоскость и рассмотрим изображение в ней. При n=m=1 для x0(1)=2l:
Ф nm=coskz+cos[k(3z-4l q
)] (22)
Оценим вклад 1-ой гармоники в сигнал для пучка молекулярного иода на длине волны 5145 Å. Для линии А2 по формулам /6/ можно получить значение дипольного момента d = 0,0032. Отсюда Y
=0.9 и контраст картины порядка 10-3 (для оценки использовались следующие значения параметров Г = 107 кГц. s = 30 мВт/см2, t
= 1o-5 c. В газе, помещенном в ячейку, контраст интерференционной картины уменьшится примерно на порядок, поскольку "работают" только атомы из "дырки Беннета", но и это значение приемлемо для эксперимента
- 179 -
Обратимся еще раз к аналогии с теневым эффектом. Если пропускание решетки, расположенной в плоскости х 1, записать в виде (½)·[1+К1х1] , то входное поле единичной амплитуды е0=ехр(ia
kx1) непосредственно за решеткой принимает вид:
e(x1)=(1/2)exp(ia
kx1)[1+cosk1x1] (23)
Здесь a
- угол между направлением волнового вектора к и нормалью к решетке. Решетка 2 расположена в плоскости х2. В плоскости наблюдения х3 поле принимает вид:
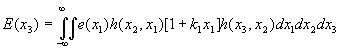
(24)
Здесь 2a
0 - ширина углового спектра поля, h(xp,xq) - импульсный отклик пространства между плоскостями xp и xq, h(xp,xq)= =exp(ikzq)exp[ik(xp-xq)2/2zq](izqλ)-1. Выполнив интегрирование в (24), получим:
e(x3 )=[λ/z1z 2(z 1+z 2)] 1/2exp[(ikx 32/2(z 1+z 3)]{1+
+ехр[- ik22z1z2/2k(z1+z2)]соs[z1x3k2/(z1+z2)]} (25)
Появление сигнала в плоскости x3 соответствует сигналу эха. Видно, что условием изображения решетки 1 в плоскости x3 являются:
k1=k2z1/(z1+z2 ); (а) [k22z 1z 2/2k(z 1+z 2)]=n p
; ( б) (26)
Первое обеспечивает формирование периода 1-ой решетки, а второе - контраст изображения. Для приложений можно записать иначе:
(z2k1k2/2k) = np
(27)
Или, переходя к периодам решеток вместо (27), получим:
(λ/L
2)/( L
2/z 2) = n (28)
Это условие означает, что для формирования сигнала эха нужно, чтобы, угол дифракции на 1-ой решетке был кратен угловому размеру 2-ой решетки. Если L
2< L
1, то всегда найдется плоскость, в
- 180 -
которой воспроизводится гармоника с частотой, меньшей, чем у 2-ой решетки. Для воспроизведения М-той гармоники нужно, чтобы k2z1(z1+z2)-1=mk1, то есть пространственная частота 2-ой решетки должна быть минимум вдвое больше, чем у 1-ой, изображение которой получаем, или в четыре раза - для 2-ой и т.д. Известно, что получение решеток в субмиллиметровой области и с меньшими λ составляет проблему.
Для ряда приложений условию (26а) удобно придать вид:
(L
1/L
2) = 1+ (z2/z1) (29)
Видно, что для z2>О период 2-ой решетки должен быть меньше, чем у 1-ой, но не обязательно вдвое, как казалось из чисто геометрических соображений. Если L
1< L
2, то условие (29) выполняется для z2<0, т.е. изображение 1-ой решетки возникает в отраженных пучках (между решетками 1 и 2). Это напоминает возникновение сигнала "мнимого эха".
Таким образом, геометрические аналогии могут быть полезны для ряда приложений.
В работе, принимали участие Б.Я.Дубецкий и В.П.Чеботаев, без обсуждений с ними, без их помощи и поддержки эта работа не появилась бы. Выражаю здесь им свою благодарность.
Л и т е р а т у р а
1. v.p.chebotayev. appl.phys. 15, 219, 1978.
2. r.l.shoemaker. in. laser and coherence spectroscopy, ed. by j.l.steinfeld (plenum press, new york, london, 1980).
3. Б.Я.Дубецкий, В.П.Чеботаев. Изв. АН СССР, сер.физ., 1986, 50, 1530.
4. Б.Я.Дубецкий, А.П.Казанцев. В.П.Чеботаев, В.П.Яковлев. 1985. ЖЭТФ. Т.89. С.1190.
5. Е.В.Бакланов, В.П.Чеботарев. 1972. ЖЭТФ. Т.62. С.541.
6. g.j.borde, g.gamy, b.decomps. phys. rev. 50, 254, 1979.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

