|
|
 |
 |

|
| |
ОПТИЧЕСКАЯ ОБРАБОТКА ИНФОРМАЦИИ В УСЛОВИЯХ
СУЩЕСТВОВАНИЯ ФАЗОВОЙ "ПАМЯТИ"
В.В.Самарцев, Л.А.Нефедьев, Д.Л.Чубаков
Обсуждаются условия реализации импульсной оптической обработки информации в резонансных средах в условиях существования в них фазовой "памяти". Анализируемые когерентные режимы обработки информации основаны на эффекте стимулированного фотонного (светового) эха. Приводятся результаты собственных экспериментов по исследованию в кристалле рубина корреляции формы эхо-сигнала с временной формой импульса-кода. Излагается методика и приводятся результаты расчета отдельных режимов оптической когерентной обработки информации.
Значительный прогресс, достигнутый в последнее время в области технических приложений фотонного эха [1] (среди этих приложений - эхо-голография; оптические запоминающие устройства на явлении долгоживущего фотонного эха с временем хранения информации более тринадцати часов [2]), позволяет поставить вопрос об оптической обработке информации в условиях существования фазовой "памяти", лежащей в основе формирования фотонного эха. Как известно [3], в случае стимулированного фотонного эха фазовая "память" в резонансной среде существует, если временной интервал t
между первой парой импульсов меньше времени поперечной необратимой релаксации Т2 и если временной интервал Т между вторым и третьим импульсами меньше времени продольной релаксации Т1. Сигнал стимулированного фотонного эха – СФЭ - излучается резонансной средой всегда через интервал времени t
после считывающего третьего импульса (т.е. в момент времени: t=t+2t
)в направлении волнового вектора (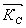 ): ):
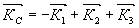 (1) (1)
где 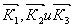 - соответственно волновое векторы 1-го, 2-го, 3-го возбуждающих импульсов. В технических приложениях наиболее - соответственно волновое векторы 1-го, 2-го, 3-го возбуждающих импульсов. В технических приложениях наиболее
- 146 -
перспективен режим, когда 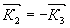 ; в этом случае ; в этом случае 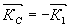 , получил название обращенного. Спектр сигнала СФЭ (sС) следующим образом связан со спектром (sh
, h
=1,2,3) возбуждающих импульсов: , получил название обращенного. Спектр сигнала СФЭ (sС) следующим образом связан со спектром (sh
, h
=1,2,3) возбуждающих импульсов:
sc=as1*s2s3 (2)
где А - константа [3]; 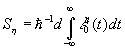
d - модуль электрического дипольного момента резонансного перехода; e
0n - амплитуда электрического поля h
-го импульса. Спектральные особенности генерации СФЭ позволяют использовать это явление в детектировании слабых импульсных сигналов или их многоимпульсных последовательностей (типа М-посдедовательности импульсов, фазы которых случайным образом принимают лишь два значения : 0 и p
), интенсивность которых ниже уровня шума. Подобные проблемы изучались в радиодиапазоне Б.Б.Устиновым с сотрудниками [4]. На резонансную среду сначала воздействует запускающий импульс (или М-последовательность), затем - слабый детектируемый сигнал (или М-последовательность той же структуры) и, наконец, - мощный импульсный сигнал (дельта-импульс, спектр которого "накрывает" всю неоднородно-уширенную линию). Согласно расчету (а в радиодиапазоне результаты расчета подтверждены экспериментом), сигнал СФЭ оказывается мощным коротким импульсом с интенсивностью выше уровня шумов, т.е. по его генерации можно судить о приходе слабого сигнала.
Первый эксперимент, в котором решалась задача оптической когерентной обработки информации, выполнен в работе [5] (и, позднее, в [6]) на кристалле рубина. Осциллограммы этого эксперимента даны на рис.1.

- 147 -

Рис.1. Осциллограммы по обнаружению эффекта корреляции временной формы СФЭ с формой импульса-кода ("К") в рубине [5] (переход: 4А2 - 2Е(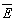 ); Т = 2,2°К; Н0 = 450Гс): а). t
= 24 нс, Т = 20 нс; б) t
= 20 нс, Т = 24 нс. Мощность импульса-кода меньше мощности остальных импульсов в 10 раз и составляет 20 квт). ); Т = 2,2°К; Н0 = 450Гс): а). t
= 24 нс, Т = 20 нс; б) t
= 20 нс, Т = 24 нс. Мощность импульса-кода меньше мощности остальных импульсов в 10 раз и составляет 20 квт).
В случае, когда импульсом-кодом является первый импульс, временная форма СФЭ обращена по отношению к форме этого импульса. Когда же импульсом-кодом является второй возбуждающий импульс, временная форма СФЭ повторяет временную форму импульса-кода. Для реализации подобных операций необходимо, чтобы для "площади" q
К импульса-кода выполнялось условие: sinq
k, где q
k =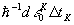 -длительность импульса-кода. Ниже будут обсуждаться некоторые варианты подобного кодирования и преобразования сигналов. Наиболее широкие возможности для их реализации открываются в многоуровневых системах. Так, в работе [7] показано, что в многоуровневой системе можно управлять длительностью кодирования сигналов и преобразовывать акустические импульсные сигналы сложной временной формы в аналогичные оптические сигналы и наоборот. Более того, эти задачи можно решать с кодируемыми волновыми фронтами [8], на что указывают первые эхо-эксперименты по обращению волнового фронта [9-11], причем такая обработка информации может быть многоканальной [12]. -длительность импульса-кода. Ниже будут обсуждаться некоторые варианты подобного кодирования и преобразования сигналов. Наиболее широкие возможности для их реализации открываются в многоуровневых системах. Так, в работе [7] показано, что в многоуровневой системе можно управлять длительностью кодирования сигналов и преобразовывать акустические импульсные сигналы сложной временной формы в аналогичные оптические сигналы и наоборот. Более того, эти задачи можно решать с кодируемыми волновыми фронтами [8], на что указывают первые эхо-эксперименты по обращению волнового фронта [9-11], причем такая обработка информации может быть многоканальной [12].
Остановимся на математическом аппарате, с помощью которого изучаются различные режимы оптической когерентной обработки информации - ОКОИ.
Методика расчета
Напряженность электрического поля h
-го импульса в виде 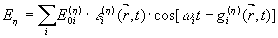 (3) (3)
- 148 -
где w
i - несущая частота, Е0 - амплитуда, gi - волновой фронт, e
i - параметр пространственно-временной неоднородности поля.
Для отыскания оператора эволюции системы u воспользуемся методом хронологического упорядочения. Следуя работе [12] , оператор u можно представить в виде: u=u1(b'h
)u2(q),
где 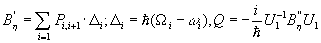 ; ;
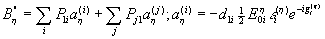
pij - проективные матрицы; dij - дипольный момент перехода "i→j". Операторы u1 и u2 определяются из системы уравнений:
du1 /dt = -i/ћb'h
u1 (4)
du2/dt = qu2 (5)
Решение уравнения (4) имеет вид:
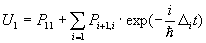 (6) (6)
а решение уравнения (5 ) представим в виде:
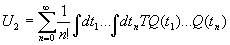
где Т - хронологический оператор Дайсона.
Проводя в (7) интегрирование и суммирование, учитывая (6), находим матрицу оператора эволюции u.
Матрицу плотности системы после воздействия h
-го импульса определяем в виде
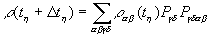 (8) (8)
где 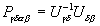 . Напряженность электрического поля отклика со сложным волновым фронтом будем искать с помощью выражения: . Напряженность электрического поля отклика со сложным волновым фронтом будем искать с помощью выражения:
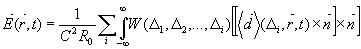 (9) (9)
- 149 -
где 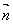 - единичный вектор в направлении наблюдения; - единичный вектор в направлении наблюдения;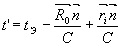 ; ; 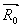 - радиус-вектор точки наблюдения; - радиус-вектор точки наблюдения;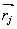 - радиус-вектор местоположения j-той частицы; w - функция формы неоднородно-уширенной резонансной линии; - радиус-вектор местоположения j-той частицы; w - функция формы неоднородно-уширенной резонансной линии;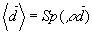 . .
Результаты расчета режимов оптической когерентной обработки информации
Проводя расчет по изложенной методике в приближении малой импульсной "площади" объектной волны, для напряженности электрического поля стимулированного эхо-сигнала имеем: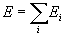
где 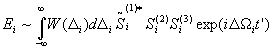
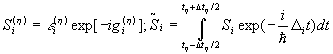
Отметим, что входящие в это выражение спектры 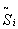 представляют собой Фурье-преобразование от свертки соответствующих спектров. Видно, что в каждом частотном канале функциональные возможности обработки сигналов аналогичны обработке сигналов в ЯМР-области, но в отличие от нее в оптике существенны условия пространственного синхронизма. Новым моментом в этом расчете, по сравнению с расчетами в радиодиапазоне [4], является учет пространственных закономерностей генерации СФЭ (в том числе при неплоских волновых фронтах импульсов). Ниже мы ограничимся режимом обращения генерации СФЭ. Варьируя временные интервалы между импульсами и порядок подачи импульса-кода по отношению к остальным импульсам, а также структуру и число входных сигналов, удается добиться реализации различных режимов ОКОИ. Часть результатов приведена в таблице. представляют собой Фурье-преобразование от свертки соответствующих спектров. Видно, что в каждом частотном канале функциональные возможности обработки сигналов аналогичны обработке сигналов в ЯМР-области, но в отличие от нее в оптике существенны условия пространственного синхронизма. Новым моментом в этом расчете, по сравнению с расчетами в радиодиапазоне [4], является учет пространственных закономерностей генерации СФЭ (в том числе при неплоских волновых фронтах импульсов). Ниже мы ограничимся режимом обращения генерации СФЭ. Варьируя временные интервалы между импульсами и порядок подачи импульса-кода по отношению к остальным импульсам, а также структуру и число входных сигналов, удается добиться реализации различных режимов ОКОИ. Часть результатов приведена в таблице.
Таблица
Некоторые варианты оптической когерентной обработки информации
|
№ |
Порядок импульсов и момент генерации СФЭ |
Операция ОКОИ |
|
1 |
2 |
3 |
|
1 |
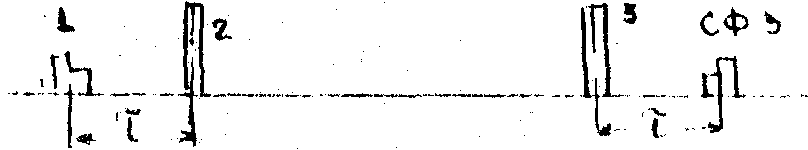
|
Обращение и задержка |
- 150 -
|
1 |
2 |
3 |
|
2
3
4
5
6 |
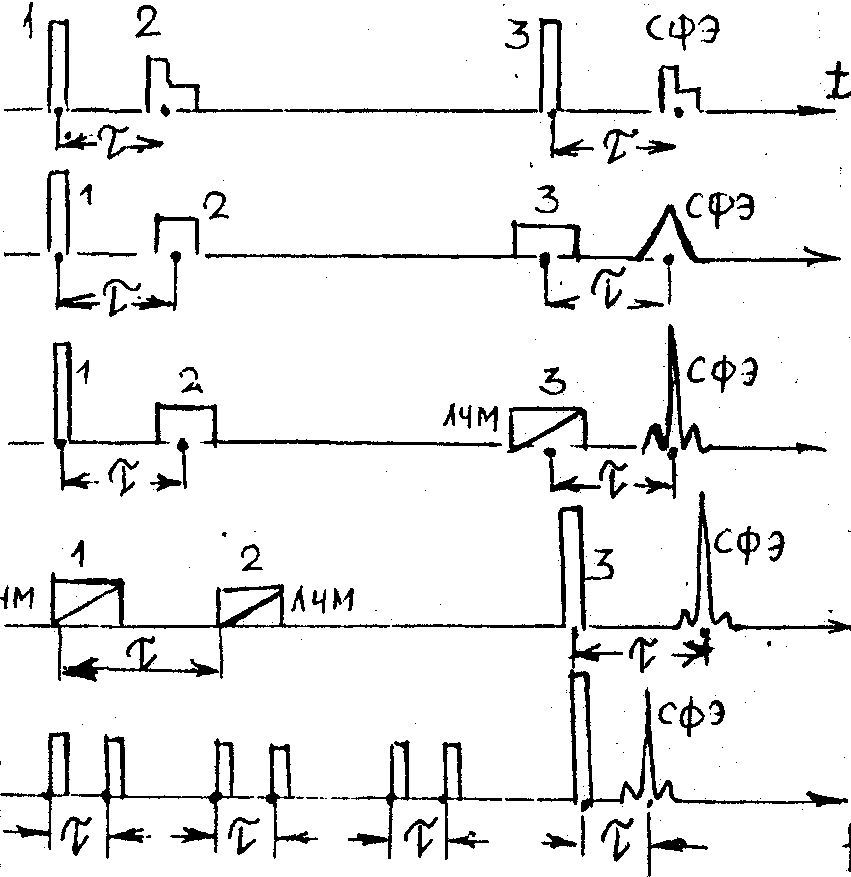
|
Задержка
Свертка
Преобразование Фурье
Преобразование Фурье
Преобразование Фурье |
Операции "1" и "2", осуществляющие обращение и задержку сигнала ("кода"), реализованы в работах [5,6 ] (Рис.1). Операция "3" позволяет получать свертку сигнала, спектр которого соответствует квадрату спектра исходного сигнала (2-го сигнала, который идентичен 3-му сигналу). Операции "4-6" осуществляют преобразование Фурье в условиях линейной частотной модуляции (ЛЧМ) импульсов и без таковой. В частности, операция "6" демонстрирует возможность когерентного сложения корреляционных откликов, образованных парами импульсов.
- 151 -
Л и т е р а т у р а
1. В.А.Голенищев-Кутузов, В.В.Самарцев, Б.М.Хабибуллин. Импульсная оптическая и акустическая когерентная спектроскопия. М.: Наука. 1988. 250с.
2. w.r.babbit, t.w. mossberg. optics communs., 1988, v.65. №3. p.185-188.
3. Э.А.Маныкин, В.В.Самарцев. Оптическая эхо-спектроскопия. М.: Наука, 1994. 270с.
4. В.Б.Устинов. Квантовые устройства обработки сигналов. Л.: ЛЭТИ. 1984, 59с.; В.Б.Устинов и др. Изв. АН СССР, сер. физ. 1986, Т.50. №8. С.1495-1498.
5. В.А.Зуйков, В.В.Самарцев, Р.Г.Усманов. Письма ЖЭТФ. 1980. Т.32. №4. С.293-297.
6. С.О.Елютин и др. ЖЭТО. 1985. Т.61. №12. С.234-244.
7. l.a.nefediev, v.v.samartsev. phya.stat.sol., 1985, v.88, №2. Р.631-635.
8. Е.И.Штырков, В.В.Самарцев. //Электромагнитное сверхизлучение. Казань.: КФ АН СССР. 1975. С.398-426.
9. c.v.heer, p.f.carlson. appl. phys. lett., 1978, v.33, №1o. Р.865-866.
10. Е.И.Штырков и др. ЖЭТФ. 1981, Т.81. №6, С.1877-1886.
11. В.А.Зуйков, Л.А.Нефедьев, В.В.Самарцев. // Прикладные вопросы голографии. Л.: ЛИЯФ. 1982. c.175-179.
12. Л.А.Нефедьев, В.В.Самарцев. Журн. Прикл. Спектр. 1987. Т.47. №4. С.640-648.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

