|
|
 |
 |

|
| |
О ТОЧНОСТИ ЗАПИСИ И ВОССТАНОВЛЕНИЯ ВОЛНОВЫХ ПОЛЕЙ
ОРТОГОНАЛЬНЫМИ ТРАНСПОРАНТАМИ
С.Г.Каленков, А.М.Смолович, Г.И.Соломахо
Рассмотрен метод Уолш-анализа волновых полей и точность их восстановления. Проведен численный эксперимент. Показано, что точность восстановления поля зависит в данном методе как от числа слагаемых в приближенном ряде Уолша, так и от апертуры транспарантов, примененных при анализе поля.
1. Метод анализа и синтеза волновых полей с помощью ортогональных Уолш-транспарантов, предложенный в работах /1—2/, основан на измерении спектральных компонент поля и дальнейшем восстановлении поля по его спектру. Напомним основную идею метода. Для этого рассмотрим общую схему формирования оптического изображения (рис.1). Пусть Е(х) - комплексная амплитуда исследуемого монохроматического волнового поля во входной плоскости оптической системы. Будем считать, что оптическая система является линейной и пусть 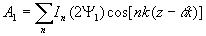 - ее импульсный отклик. - ее импульсный отклик.
Комплексная амплитуда в точке x
0 выходной плоскости системы может быть записана в виде
g(x)=ò
e(x)h(x1x
0)dx (1)
Интегрирование осуществляется по входной апертуре. Здесь и ниже под х и x
мы понимаем пару координат точки, соответственно, во входной плоскости (в пределах апертуры) и в выходной плоскости оптической систему. Пусть во входной плоскости х установлен транспарант с функцией пропускания Т h(х) (индекс h нумерует транспаранты). Тогда комплексная амплитуда поля g(x
0) в точке x
0 выходной плоскости изменится и станет равной
- 5 -
gh(x
0)=ò
th(x)e(x)h(x1x
0)dx (2)
Введем обозначение
eh(x,x
0)=e(x)h(x,x
0) (3)
и запишем (2) в виде
gh(x
0)=ò
th(x)eh(x,x
0)dx (4)
Пусть функции пропускания транспарантов образуют полную ортонормированную систему функций {th(x)}, заданных на входной апертуре оптической системы. Тогда набор величин {gh(x
0)} определяемых выражением (4), образует спектр поля eh(x,x
0). Иначе говоря, определив комплексные амплитуды поля в одной и той же точке x
0 выходной плоскости при разных транспарантах th(x) мы определяем коэффициенты разложения функции eh(x,x
0) по набору ортонормированных функций {th(x)}. Если эта задача решена, т.е. найден набор коэффициентов {gh(x
0)}, то известна и функция eh(x,x
0) так как по смыслу gh(x
0)
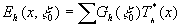 (5) (5)
(*- означает знак комплексного сопряжения), а, следовательно, в принципе, и комплексная амплитуда Е(х)-волны на входной апертуре оптической системы, так как
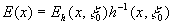 (6) (6)
Непосредственно измерить комплексные амплитуды 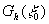 не удается, т.к. установленный в точке не удается, т.к. установленный в точке 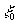 детектор с малой (точечной) апертурой измеряет интенсивность детектор с малой (точечной) апертурой измеряет интенсивность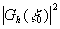 , т.е. квадрат модуля спектральных коэффициентов. , т.е. квадрат модуля спектральных коэффициентов.
Решить задачу измерения комплексных амплитуд 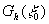 удается, вводя наборы транспарантов с несколько измененными функциями пропускания: удается, вводя наборы транспарантов с несколько измененными функциями пропускания:
- 6 -
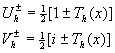 (7) (7)
Легко видеть, что если во входной плоскости установлен транспарант, функция пропускания которого есть 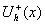 , то измеренный в точке , то измеренный в точке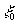 сигнал, равен сигнал, равен
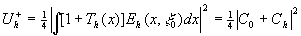 , (8) , (8)
где
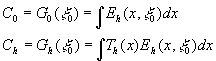 (9) (9)
- коэффициенты разложения функции 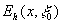 по системе функций {Тh по системе функций {Тh(x) }. Аналогично, для транспаранта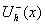 получаем сигнал получаем сигнал
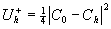
(10)
Разность величин этих сигналов есть
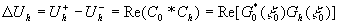 (11) (11)
Для транспарантов с функциями пропускания 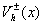 из набора(7) величины соответствующих сигналов из набора(7) величины соответствующих сигналов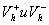 равны: равны:
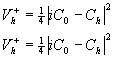
(12)
- 7 -
а их разность
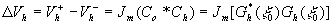 (13) (13)
Таким образом, с помощью набора транспарантов (7) можно измерить (с точностью до постоянного комплексного коэффициента 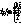 все спектральные коэффициенты разложения функции все спектральные коэффициенты разложения функции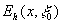 и представить ее рядом и представить ее рядом
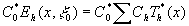 (14) (14)
Это означает, что в принципе данная измерительная процедура позволяет восстановить Е(х), т.е. определить комплексную амплитуду волнового поля на входной апертуре оптической системы. Это может быть, очевидно, сделано численным методом с помощью ЭВМ. Как показано в /2/ поле Е(х) может быть восстановлено путем синтеза голограммы. Особенно удобно для этих целей использовать систему бинарных ортонормированных функций, принимающих лишь два значения +1 и -1, например, систему функций Уолша 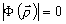 определение и свойства которых даны, например, в книге /3/. определение и свойства которых даны, например, в книге /3/.
2. Близким к рассмотренному выше является осуществленный недавно в работе /4/ метод спектрального анализа волнового поля с помощью трехмерной голограммы. В этой работе была экспериментально продемонстрирована способность глубокой трехмерной голограммы оптически осуществлять спектральное разложение волнового поля по системе ортогональных функций Уолта. Запись голографического фильтра осуществлялась в /4/ поэтапно, так что на одной трехмерной голограмме записывался массив голограмм Фурье, обладающий фильтрующими свойствами для заданного на входной апертуре набора функций Уолша. Поскольку каждая из голограмм записывается на своей пространственной несущей, то на стадии восстановления образы, соответствующие различным Уолш-компонентам
- 8 –
объектного поля, оказываются пространственно разнесенными в выходной плоскости. Это и дает возможность определять величины модулей спектральных компонент объектного поля. Задача определения фазы спектральных коэффициентов в /4/ не ставилась.
3. Для практических применений , необходимо оценить точность восстановления волнового поля, спектр которого определяется с помощью описанной выше методики. Здесь имеется ряд вопросов принципиального характера. Один из распространенных критериев точности восстановления поля состоит в сравнении с единицей величины проекции восстановленного поля u на правильное(исходное) поле 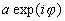 : :
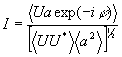 (15) (15)
Здесь угловые скобки означают усреднение по пространственной координате. Ясно, что чем ближе величина i к единице, тем точнее восстановление поля. Тем не менее, остается неясным, когда точность восстановления можно считать достаточной, поскольку ответ на этот вопрос зависит от специфики решаемой задачи.
Обсудим этот вопрос подробнее. Определив спектр, т.е. набор коэффициентов { ch} мы можем восстановить объектное поле. Строго говоря, при этом мы восстанавливаем это поле только на входной апертуре оптической системы. При этом восстановить поле можно тем точнее, чем больше измерено коэффициентов Сh. При восстановлении мы пока понимаем чисто математическую операцию построения функции по ее известному спектру. Далее для определенности рассматривается Уолш-спектр, т.е. предполагается, что набор функций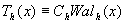 - есть набор функций Уолша, заданных на апертуре транспаранта. Таким образом, восстановленное с помощью набора из n транспарантов поле описывается функцией вида - есть набор функций Уолша, заданных на апертуре транспаранта. Таким образом, восстановленное с помощью набора из n транспарантов поле описывается функцией вида
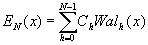 (16) (16)
- 9 -
Предположим, что задача состоит в том, чтобы по восстановленному объектному полю Е n (х) распознать образ самого объекта. Ясно, что в этом случае важную роль играет не только (и не столько) точность восстановления объектного поля, но и размер апертуры, на которой записывается и восстанавливается это поле.
В качестве иллюстрации можно привести такой пример. Пусть объект - длинная светящаяся щель, а объектное поле в плоскости х имеет вид:
Е(х )= sinС ах (17)
где коэффициент а определяется геометрией задачи и длиной волны λ. Если апертура d транспаранта мала, d <<i/a, то объектное поле (17) на данной апертуре практически постоянно, а именно, e≈l. Чтобы выявить отличие Е от единицы, необходимо на данной малой апертуре измерить с высокой точностью ее спектральные коэффициенты Сh с использованием большого количества транспарантов.
Если взять большую апертуру, например, d = 4/a, то, как видно из рис.2, на этой апертуре информация о функции существенно более полная. Следовательно, можно надеяться, что меньшим числом транспарантов на такой апертуре можно измерить функцию Е(х) с меньшей точностью, но при этом восстановленное поле будет содержать больше информации об объекте. Из данного примера ясно, что интегральный критерий типа (15) не является достаточным для задачи распознания образа по восстановленному объектному полю. Более существенно, чтобы общий характер распределения (по апертуре) восстановленного поля был близок к распределению истинного объектного поля. Интегральные критерии типа (15) полезны для контроля правильности восстановления поля и в этом смысле являются вспомогательными.
В соответствии с изложенным качественным подходом был проведен численный эксперимент по восстановлению методом Уолш-анализа комплексной амплитуды поля. Точность восстановления исследовалась в зависимости от величины апертуры Уолш-транспарантов и от их числа n. В качестве модельного было выбрано поле.
- 10 -
формируемое (в приближении Френеля) плоской волной, проходящей через две параллельные щели. Аналитический вид этого поля хорошо известен. Однако, оно имеет достаточно сложную структуру, что делает его удобным как объект исследования. Для оценки результатов применялись также следующие интегральные критерии: не содержащий фазовой информации "энергетический" критерий i 1,
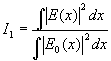 (18) (18)
и зависящий от фазы нормированный интеграл перекрытия
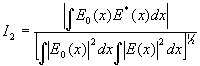 (19) (19)
Здесь Ео(х) - точное модельное поле, Е(х)≡Е n(х) в (16), т.е. восстановленное поле.
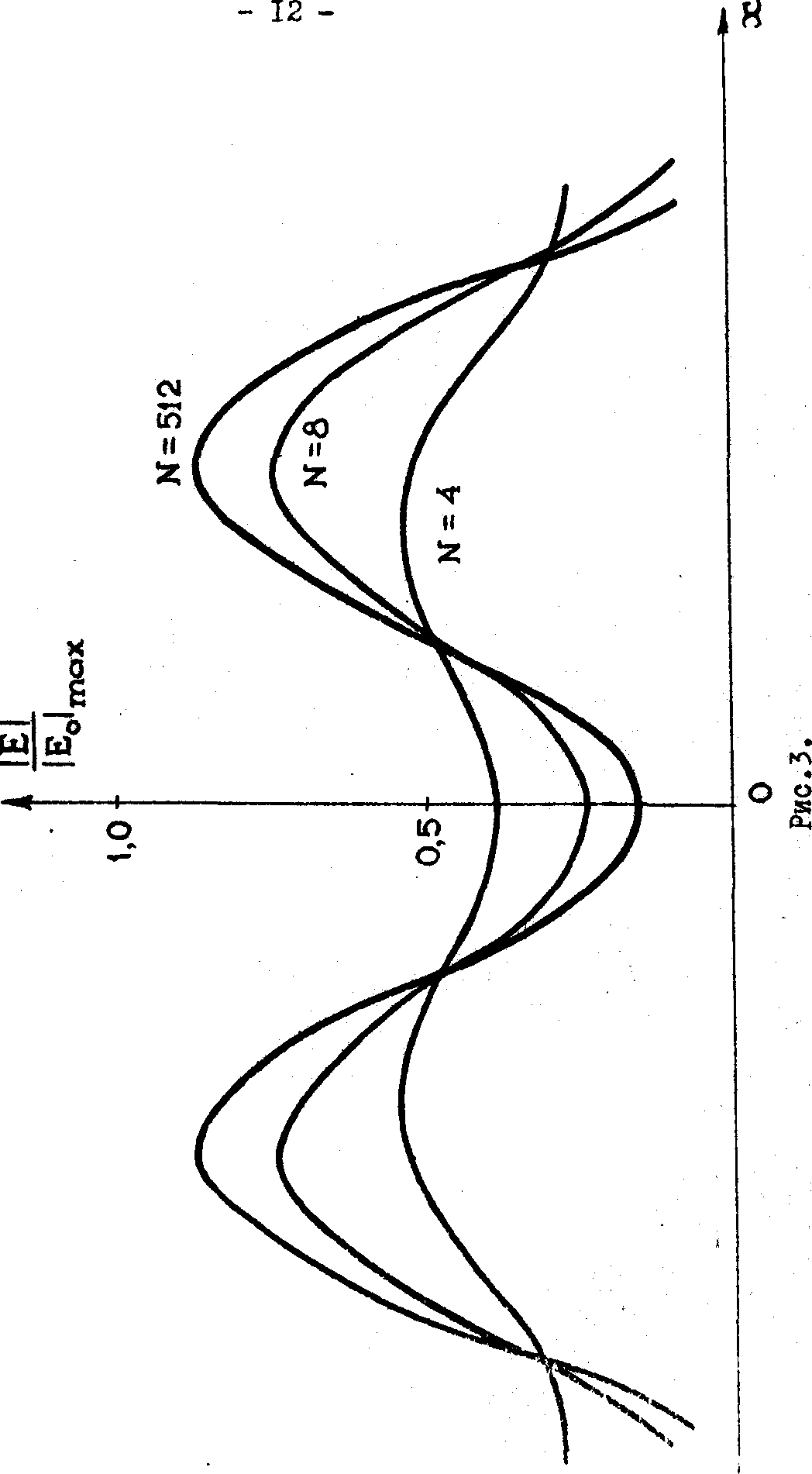
В результате численного эксперимента подтвердилось предположение о необходимости выбора при процедуре записи и восстановления поля достаточно большой апертуры Уолш-транспарантов. При слишком малой апертуре рост числа n транспарантов практически не влияет на точность восстановления. Она остается низкой и по характеру распределения поля по апертуре, и по критериям (18) и (19). Критерий малости апертуры в данном случае соответствует критерию разрешения по Аббе. При правильном выборе апертуры Уолш-транспарантов, т.е. при их достаточной величине, высокая точность восстановления обеспечивается малым числом транспарантов n~10-100: число их варьируется в зависимости от геометрии задачи. В качестве примера на рис.3 приведена зависимость безразмерной амплитуды восстановленного поля от координат в плоскости изображения. На рис.4 дана зависимость величины интегральных критериев i1 и i2 от числа n, использованных в процедуре восстановления Уолш-транспарантов. Геометрия задачи в обоих случаях одинакова, причем апертура транспарантов достаточна для разрешения по критерию Аббе.
- 11 -
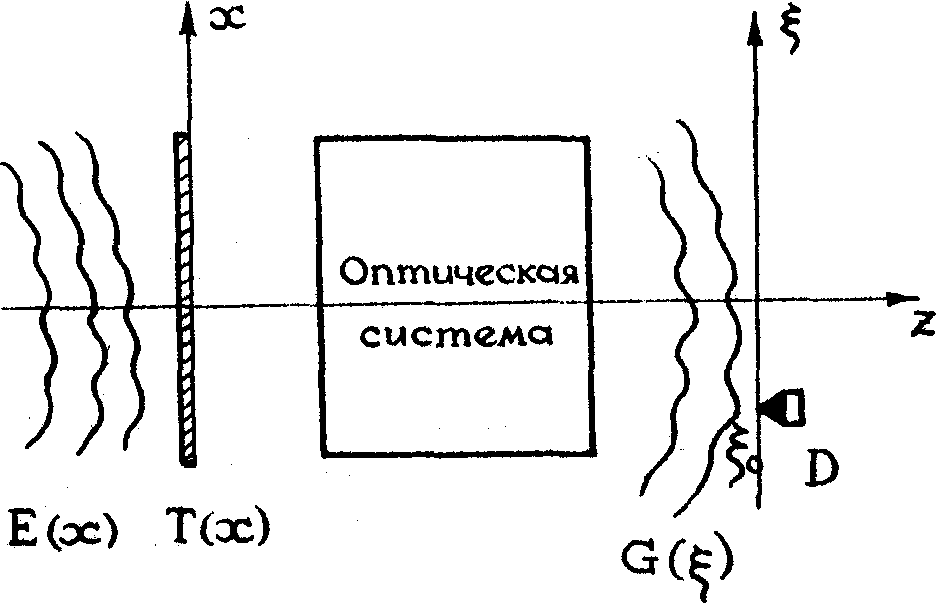
Рис.1.
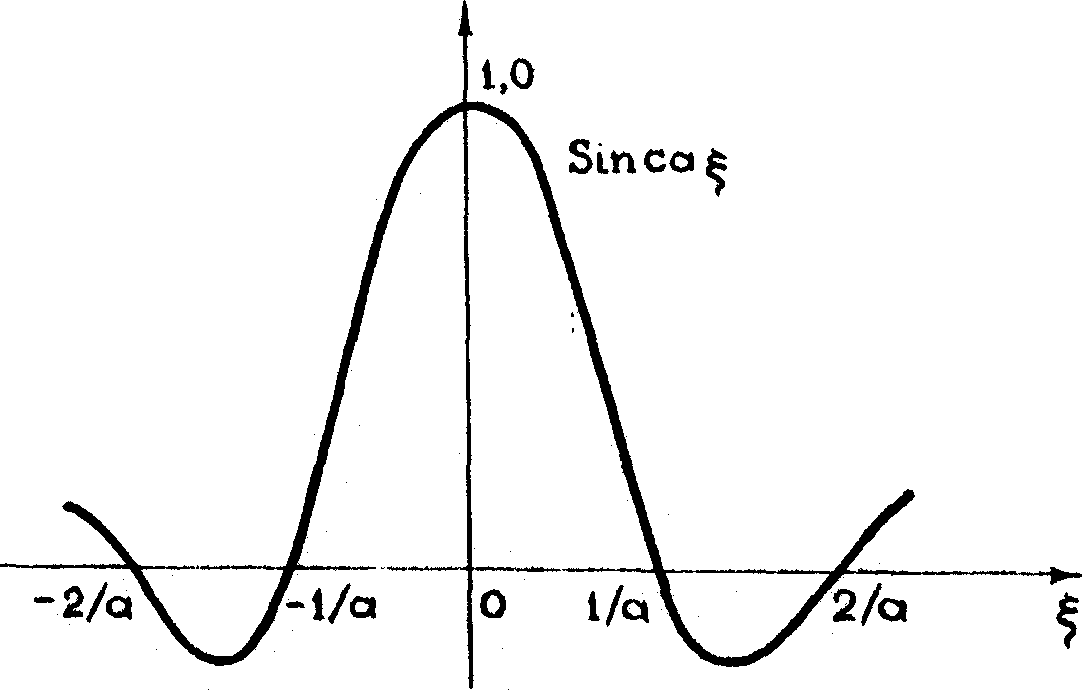
Рис.2.
- 13 -
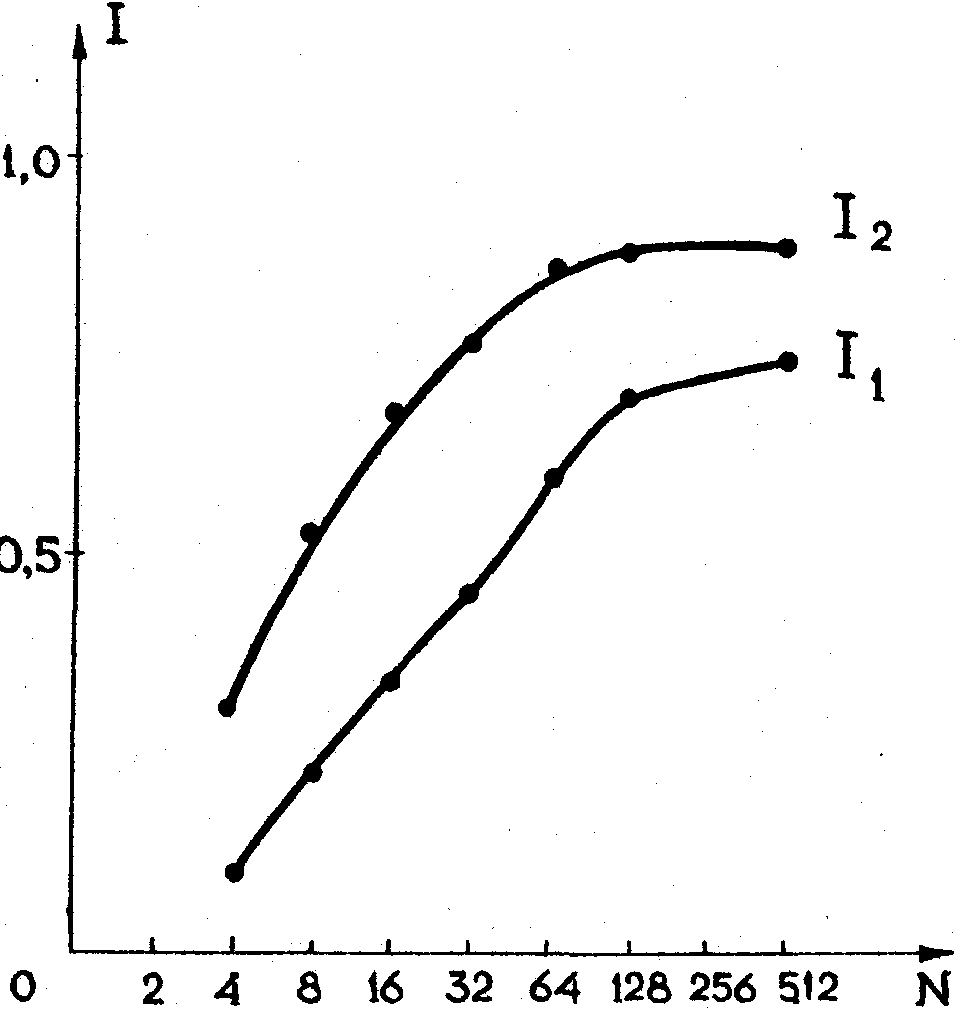
Рис .4.
- 14 -
Таким образом, можно сделать вывод, что метод Уолш-аналиэа и восстановления волновых полей может быть достаточно эффективным. При этом для построения соответствующих оптоэлектронных систем полезно использовать априорную информацию о качественной структуре поля.
Л и т е р а т у р а
1. Н.И.Дмитриев, С.Г.Каленков, Г.И.Соломахо. Уолш-анализ волновых полей. // Физические основы и прикладные вопросы голографии. Л., 1984. С.19-26.
2. Н.И.Дмитриев, С.Г.Каленков, Г.И.Соломахо. Регистрация и синтез голограмм ортогональными транспарантами. Автометрия. 1987. №2. С.24-28.
3. Х.Ф.Хармут. Теория секвентного анализа - М.: Мир. 1980.
4. Ю.Н.Денисюк, И.Н.Давыдова. // Оптическая голография с записью в трехмерных средах (ред. Денисюк Ю.Н.) Л.: Наука. 1986. С.9-17.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

