|
|
 |
 |

|
| |
КОГЕРЕНТНЫЕ ОПТИЧЕСКИЕ И АКУСТООПТИЧЕСКИЕ ФУРЬЕ-ПРОЦЕССОРЫ
С УЧЕТОМ ДИСООТАТИВНОСТИ СРЕД
О.Д.Москалец
Рассмотрена дифракция Френеля и Фраунгофера в однородной изотропной диссипативной среде на основе методов теории линейных систем, для чего доказана обосновывающая интеграл суперпозиции теорема.
Определено акустическое поле в среде акустооптического взаимодействия при неразрывном учете дифракционной расходимости и диссипации. Показано, что спектры комплексных частот - следствие диссипации соответствующих волн.
Обобщение положений теории дифракции на случай однородной изотропной диссипативной среды (ОИДС) возможно при комплексном волновом числе 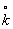 =k1+ik2 (k2>0, 2p
k2<<k1), для которого уравнение Гельмгольца также имеет решение /1/. Функция Грина g ОИДС, определенная из уравнения Ñ
2 =k1+ik2 (k2>0, 2p
k2<<k1), для которого уравнение Гельмгольца также имеет решение /1/. Функция Грина g ОИДС, определенная из уравнения Ñ
2g+ 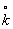 2 2g=-4 p
d
( 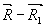 ) , описывает экспоненциально затухающую расходящуюся сферическую волну;
g(r)=exp(-k2r)·exp(ik1r)·r-1 r=ï
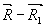 ï ï
(1)
где 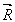 =(x
,h
, =(x
,h
,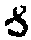 ), ),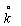 =(x
',h
', =(x
',h
',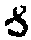 1) x
,h
, 1) x
,h
,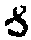 1 - декартовы координаты, условие излучения Зоммерфельда выполняется строго. 1 - декартовы координаты, условие излучения Зоммерфельда выполняется строго.
Дифракционное поле в зонах Френеля и Фраунгофера можно выразить, исходя из (1), либо применяя выкладки теории дифракции, либо методы теории линейных систем /2/, где линейный оператор
z: x→y отображает пространство входов Х'
x в пространстве выходов y'
y. Такой подход широко применяется в когерентных
- 189 -
системах оптической обработки информации и в голографии, например, /2,З/, где z называется интегралом суперпозиции и записывается в виде
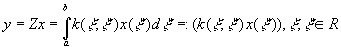 (2) (2)
и легко обобщается на x
,x
'Î
rn. Это важнейшее соотношение теории линейных систем не имеет строгого обоснования для общего случая. Так, в литературе по когерентной оптике и голографии /2,3/ предложен следующий вывод (1):
x(x
)=(x*d
)(x
)Þ
zx=z(x*d
)=(zd
,x)
где * - символ свертки. Последнее равенство далеко не очевидно, т.к. не вытекает из общих свойств свертки (например отображения, некоммутирующего со сверткой, - оператор увеличения функции), а ядро k(x
,x
')=zd
(x
-x
') требует определения. Ввиду важности (1) в линейной теории и, в частности, для когерентных оптических систем докажем, что имеет место свойство свертки с d
-функцией: z(x*d
)=(zd
,x) при надлежащем определении k(x
,x
'), т.е. справедлива Теорема: Пусть l2э k(x
,x
')= zd
n(x
-x
'),x
,x
'Î
(a,b), zd
n(x
-x
'),x
,x
'Î
(a,b), 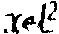 , z - линейный непрерывный оператор в l2 и существует x*d
, хотя бы в А', тогда операторы z и свертывания перестановочны. , z - линейный непрерывный оператор в l2 и существует x*d
, хотя бы в А', тогда операторы z и свертывания перестановочны.
Доказательство основано: 1) на строгом разложении обобщенной функции ¦
Î
a' в ряд ¦
=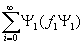 , сходящийся в пространстве обобщенных функций a', {Y
i}i¥
- полная ортонормальная система в l2 собственных функций некоторого линейного самосопряженного дифференциального оператора /4/; 2) на теоремах и обозначениях /5/. , сходящийся в пространстве обобщенных функций a', {Y
i}i¥
- полная ортонормальная система в l2 собственных функций некоторого линейного самосопряженного дифференциального оператора /4/; 2) на теоремах и обозначениях /5/.
Рассмотрим линейный оператор j
x=(k,x), d
Î
a' Þ
Þ
d
(x
-x
')=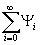 (x
)Y
i*(x
')Þ
k(x
,x
') (x
)Y
i*(x
')Þ
k(x
,x
') z z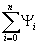 (x
)Y
i*(x
') (x
)Y
i*(x
') и последовательность вырожденных ядер kn(x
,x
')=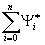 (x
')zY
i(x
) → k(x
,x
') при n→∞ порождает последовательность j
n (x
')zY
i(x
) → k(x
,x
') при n→∞ порождает последовательность j
n(x) , такую, что ║j
n(x)-j
(x)║£
ï
kn-kï
║x║→0 при n→∞. С другой стороны, j
n(x) = =(k n,x)=z 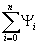 (x iY
i)=zx n, ║zx n-zx║→0 при n→∞. Предельный переход в последнем равенстве при n→∞ дает j
=z и z(x*d
)=(z,d
,x)
- 190 -
Выражение дифракционного поля Френеля в ОИДС, полученное методами теории линейных систем /2/, а точнее, на основе доказанной теоремы:
v (x
,h
,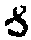 )= )=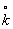 exp(i exp(i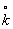 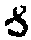 )(2p
i )(2p
i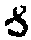 )-1 )-1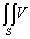 (x
',h
')exp{i (x
',h
')exp{i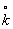 [(x
-x
')2+ [(x
-x
')2+
+(h
-h
')2]( 2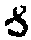 )-1}dx
'dh
' (3) )-1}dx
'dh
' (3)
совпадает, разумеется, с результатами применения теоремы Кирхгофа-Гельмгольца. Перейдем к дифракции Фраунгофера в ОИДС:
v(x
,h
,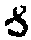 )= )=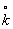 exp(-k2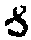 )exp(ik1 )exp(ik1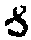 )exp[-k2(x
2+h
2)(2 )exp[-k2(x
2+h
2)(2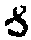 )-1]exp[ik1(x
2+ )-1]exp[ik1(x
2+
+h
2)( 2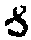 )-1] (2p
i )-1] (2p
i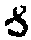 )-1 )-1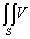 (x
',h
')exp[i (x
',h
')exp[i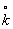 (x
+h
) (x
+h
)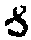 -1 -1]d x
'd h
'
где интеграл определяет преобразование Фурье в комплексной области, сомножитель exp[-k2(x
2+h
2)(2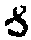 )-1] обеспечивает существование (4). )-1] обеспечивает существование (4).
Дифракция - одно из главных физических явлений, используемых в оптической обработке информации, и в этом смысле (3), (4) будут одними из основных соотношений в ОИДС, и (3) позволяет определить спектр статического сигнала на выходе когерентного оптического Фурье-процессора, если слои свободного пространства заменить ОИДС /6/:
Ф(x
2)=bexp[(i 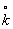 x
22 x
22)(2f) -1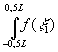 exp[(i 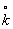 x
12 x
12)(2f) -1·
·exp[(i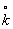 x
1x
2)f-1]dx
1 (5) x
1x
2)f-1]dx
1 (5)
где cэb=const - апертура оптической системы, 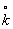 x
2f-1=w
x+is
x - комплексная пространственная частота is
x обусловлено диссипацией световой волны, f - фокусное расстояние. Если в (5) перейти к временным переменным, то получаемая электрооптическая аналогия /2/ означает последовательный гетеродинный анализатор спектра (АС) "со сжатием" в узкополосном тракте, который переходит либо в последовательный гетеродинный АС, если k1→0, либо в дисперсионно-временной АС при k2→0, последнее соответствует x
2f-1=w
x+is
x - комплексная пространственная частота is
x обусловлено диссипацией световой волны, f - фокусное расстояние. Если в (5) перейти к временным переменным, то получаемая электрооптическая аналогия /2/ означает последовательный гетеродинный анализатор спектра (АС) "со сжатием" в узкополосном тракте, который переходит либо в последовательный гетеродинный АС, если k1→0, либо в дисперсионно-временной АС при k2→0, последнее соответствует
- 191 -
приведенной аналогии в /2/.
Одно из важнейших применений (3) - это возможность описать и рассчитать акустическое поле в среде акустооптического (АО) взаимодействия АО модулятора - устройства ввода динамического сигнала в когерентный оптический фурье-процессор при неразрывном учете дифракционной расходимости и диссипации акустического пучка. Обычно эти искажающие факторы учитывались порознь, их совместное рассмотрение дает (3), и акустическая волна выражается через табулированные функции f(z) /7/:
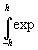 [i [i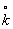 (x
-x
')2(2 (x
-x
')2(2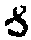 )-1]dx
1=[i )-1]dx
1=[i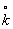 (2 (2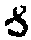 )-1]0,5[f(z1)-f(z2)], )-1]0,5[f(z1)-f(z2)],
z1,2=i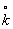 (h±
x
)2(2 (h±
x
)2(2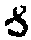 )-1 )-1 . При больших ï
zï
=r
и 0,25p
<argz=q
<0,5p
f(z)=(i 0,5p
)0,5exp(z2)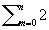 (m-1)![2m+1 (m-1)![2m+1z 2m+1] -1+r n, ï
r nï
£
[exp( r
2· ·cosq
)(2n+1)!][2n+32(2n+1)r
2n+1sinq
]-1, откуда следует, и это иллюстрируют численные расчеты, что с ростом 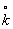 2 уменьшается отклонение функции v(x
,h
, 2 уменьшается отклонение функции v(x
,h
,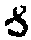 ), вызванное дифракционной расходимостью, от параллелепипеда, основание которого - прямоугольный пьезо-преобразователь размерами hхℓ. Это подтверждает допустимость игнорирования дифракционной расходимости акустического пучка при существенной диссипации. Такая возможность аппроксимации акустического поля в среде АО взаимодействия позволяет получить аппаратную функцию спектрального прибора в самом общем виде /8/: ), вызванное дифракционной расходимостью, от параллелепипеда, основание которого - прямоугольный пьезо-преобразователь размерами hхℓ. Это подтверждает допустимость игнорирования дифракционной расходимости акустического пучка при существенной диссипации. Такая возможность аппроксимации акустического поля в среде АО взаимодействия позволяет получить аппаратную функцию спектрального прибора в самом общем виде /8/:
kx
(x
2w
,W
',t)=zsd
(W
-W
')=a1 exp[i(w
+W
)t]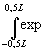 {i[w
x
2(cf)-1+ {i[w
x
2(cf)-1+
+ k1(W
')+ik2(W
')]x
'}dx
'Û
kt(W
,W
',t)=a2exp[i(w
+W
')t] (6)
где W
и w
- круговые частоты звука и света, соответственно, t - время, x
2 - координата в выходной плоскости, l - апертура, k1= =W
'vгр-1( W
') , f - фокусное расстояние, Сэa1, a2=const, t= lvгр-1· ·( W
-1), W
1'< W
0'< W
2', ( W
2'- W
1') - полоса анализа. Согласно (2),
- 192 -
аппаратурный спектр динамического сигнала F
x
=(kx
,F
0), F
t=(kt,F
0), F
0( W
') - спектр анализируемого динамического сигнала, а kt определяется наиболее общим видом интеграла, зависящего от параметра W
'. Из (6) следуют важные вывода: kx
,t в форме (6) возможно лишь в линейном режиме АО-взаимодействия /8/, т.е. при известном снижении динамического диапазона d<do АО АС. Уменьшение l(k2(W
')l), l<l0, и сужение ΔW
=W
2'-W
1'<ΔW
позволяет пренебречь изменениями k1(W
') и влиянием k2(W
')x
, тогда, в приближении тени для акустического поля в среде АО взаимодействия имеем k в виде /9/
k1(W
,W
',t)=aexp[i(w
+W
')t]sinc[(W
-W
')0,5t],W
,W
'=var (7)
где W
=w
vx
1(cf)-1 - временная спектральная частота, t=lvF
-1 - время анализа /9/. Выражением (7) дается комплексная аппаратная функция идеального /9/ АО АС, вычисляющего мгновенный спектр F
(W
,t), сомножитель ехр(·) определяет линейный фазовый член как результат анализа на нестационарном отрезке [t-0,5t,t+o,5t], а slnc(·) - спектр гармонического колебания, вычисленный за время Т. Соотношение (7) стало возможным при tΔW
d0,5p
-1=t 0ΔW
0d 00,5p
, v, v0 - объем сигнала.
АС с аппаратной функцией (7), где, t может быть как континуумом, так и счетным множеством {tn} (результат анализа на нестационарном отрезке [tn-0,5t,tn+0,5t], назовем АС Фурье, если (7) возможно при адекватном уменьшении v0, то kx
(6) можно представить рядом, перейдя к безразмерным переменным и применив методы теории вытянутых волновых сфероидальных функций, как сделано в /10,11/, т.е.
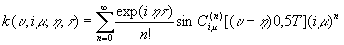 (8) (8)
где u
(x
2) и m
(x
2) - вещественная и мнимая составляющие безразмерной спектральной частоты. При этом F
t
(u
+im
,t
)=(k(u
,m
,h
,t
)F
0(h
)).
Аппаратные функции АО АС (6),(7) получены, когда w
=const, W
'=var, если W
'=W
=const, w
=w
'= var, то получающееся соотношение определяет комплексную аппаратную функцию спектрометра оптического диапазона /11/. Это проявление "принципа
- 193 -
билинейности" акустооптического взаимодействия /12/. Изложение этого вопроса выходит за рамки настоящей работы, и здесь лишь отметим, что оптические когерентные методы обработки информации позволили по-новому взглянуть на оптический спектрометр /11/ и показать, что в его выходной плоскости формируется мгновенный спектр оптического излучения /11/.
Л и т е р а т у р а
1. Владимиров b.c. Уравнения математической физики. М., Наука. 1971. С.264.
2. Папулис А. Теория систем и преобразований в оптике. М., Мир, 1971, c.271.
3. Юy Ф.Т.С. Введение в теорию дифракции, обработку информации и голографию. М., Сов.радио, 1979, С.254.
4. Земанян А.Г. Интегральные преобразования обобщенных функций. М., Наука, 1974, С.321.
5. Рисс Ф., Сёкефальви-Надь Б. Лекции по функциональному анализу. М., Мир. 1979, С.427.
6. Москалец О.Д. Пространственные спектры комплексного аргумента в оптическом когерентном процессоре // v Всес.школа по оптической обработке информации. Тез.докл., Киев, 1984, С.31-32.
7. Карпов К.А. Таблицы функций f(z)=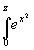 dx в комплексной области. М., АН СССР, 1958. 324 с. dx в комплексной области. М., АН СССР, 1958. 324 с.
8. Москалец О.Д. Теоретическое исследование некоторых вопросов анализа комплексного и энергетического спектров акустооптическим устройством // Методы и устройства радио- и акустической голографии. Л., Наука, 1983, с.102-109.
9. Кулаков С.В., Москалец О.Д., Разживин Б.П. Некоторые вопросы теории оптико-акустического анализатора спектра // Труды ЛИАП, Л., 1969. вып.64, С.43-52.
10. Москалец О.Д. Накопление мгновенных спектров в радиоастрономии // iii Всес.конф. Метрологическое обеспечение антенных измерений. Тео.докл. Ереван,.1984, С.82-84.
- 194 -
11. Москалец О.Д. Об измерении энергетических спектров случайных процессов в радио- и оптическом диапазоне / / ii Всес.симп. Статистические измерения и применение микромашинных средств в измерениях. 1 секция. Тез.докл. Рига, 1984 – Л., 1984, с.60-66.
12. Москалец О.Д. Один из видов дифракции света на акустических волнах как билинейное преобразование // Материалы xii Всес.конф. по акустоэлектронике и квантовой акустике. Часть 1, Саратов. 1983. С.286-287
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

