|
|
 |
 |

|
| |
ВОССТАНОВЛЕНИЕ ИЗОБРАЖЕНИЙ С ПОМОШЬЮ
АМПЛИТУДНО-ФАЗОВЫХ СООТНОШЕНИЙ
Г.А.Акимова, В.В.Матайбаев, Ю.П.Сырых, А.В.Фролов
Рассматривается решение задачи восстановления фазы дифракционного поля по его амплитудному распределению в двумерном случае. Приводятся результаты исследований по восстановлению изображения при регистрации спектра с аддитивным амплитудным шумом и мультипликативным фазовым искажением объектного поля. Описаны также результаты обработки дифракционной картины, полученной в реальном эксперименте .
Во многих задачах физики регистрации доступно фурье-преобразование какой-либо величины, в то время как требуется знать саму эту величину. В оптике исследуемой величиной является распределение поля на объекте, а измеряемой - его пространственный спектр (дифракционное поле в дальней зоне). Если есть возможность измерять интенсивность и фазу спектра с требуемой точностью, то не возникает серьезных проблем в определении величины объектного поля. Однако, условия регистрации сигнала нередко таковы, что измерению доступна только часть информации - амплитуда, либо фаза рассеянного поля. Поэтому естественно желание исследователей восстановить недостающее распределение по имеющимся данным. Такой задачей и является "фазовая проблема" - задача восстановления фазовой информации по амплитудным данным /i/. Ее решение считается найденным, если удается восстановить изображение объекта с точностью до инверсии и линейного сдвига.
Данную задачу можно сформулировать следующим образом. Пусть 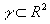 - ограниченная область. Требуется определить функцию f(х), f(x)Î
l2, в общем случае комплексную, по величине амплитуды |f(u)|, где - ограниченная область. Требуется определить функцию f(х), f(x)Î
l2, в общем случае комплексную, по величине амплитуды |f(u)|, где
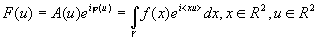 (1) (1)
- 16 -
Здесь u и x - соответствуют декартовым координатам в спектральной и объектной плоскостях, соответственно.
Вопрос об однозначности решения указанной задачи достаточно сложен и до настоящего времени не решен (см., например, /2/). В данной работе мы не будем касаться этого вопроса.
Для решения задачи восстановления изображения объекта (амплитуды светового поля) широкое распространение получили итерационные алгоритмы, в частности, алгоритм сокращения ошибки /3/. Однако их эффективность существенно зависит от степени близости начального приближения к решению, наличия априорной информации и ее точности. Имеющиеся искажения приводят к снижению скорости сходимости процедуры, что, по существу, делает невозможным непосредственное использование этих методов для обработки реальных данных. Кроме того, такая информация, как размер носителя, как правило, отсутствует и оценивается по размеру автокорреляционного объекта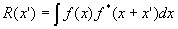 с низкой точностью. Поэтому возникает необходимость вычисления первоначальной оценки изображения для итерационной процедуры. Чтобы решить эту задачу нами предложено использовать в качестве начального приближения пробную функцию, полученную путем восстановления фазы с помощью двумерного амплитудно-фазового преобразования /4/. Возможность получения таких соотношений обусловлена тем, что функцию f(u), u=(u1 с низкой точностью. Поэтому возникает необходимость вычисления первоначальной оценки изображения для итерационной процедуры. Чтобы решить эту задачу нами предложено использовать в качестве начального приближения пробную функцию, полученную путем восстановления фазы с помощью двумерного амплитудно-фазового преобразования /4/. Возможность получения таких соотношений обусловлена тем, что функцию f(u), u=(u1,u 2) можно аналитически продолжить в комплексную плоскость по каждой из переменных z1=u1+iv1, z2=u2+iv2 как целую функцию конечной степени /5/. Следует ответить, что амплитудно-фазовые соотношения в общем виде до сих пор не установлены. В случае, когда нули функции f(z1,z2) расположены только в одной полуплоскости каждого из переменных, т.е. при imz1≤0, imz2≤0, эти соотношения известны /6/:
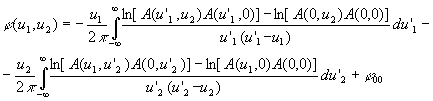 (2) (2)
- 17 -
В общем случае нет никаких оснований полагать, что такие условия выполняются достаточно часто. Тем не менее, двумерный случай имеет ряд специфических особенностей. Главная из них со -стоит в том, что множество нулей функций двух переменных f( z1,z2) в отличие от одномерного случая, представляет собой гиперповерхность в пространстве z1хz2 /5/. В этом случае положение нулей f(z1,z2) по переменным z1 и z2 связаны между собой и не могут перебрасываться независимо друг от друга в комплексно сопряженное положение. В результате применения соотношения (2) происходит переброс части нулевого множества, при этом формируется распределение, амплитуда и фаза которого связаны, но нули в области imz1>0, imz2>0 отсутствуют. Таким образом, в силу построения формируется целая функция, которая удовлетворяет тем же условиям, что и искомая, но не имеет нулей в заданной области. Это означает, что применение соотношения (2) позволит достигнуть приближенное восстановление изображения. Затем изображение можно скорректировать с помощью итерационной процедуры. Именно такой подход был использован нами.
При численной реализации выражения (2) использовалось следующее соотношение:
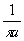 =Ŧ{signx} =Ŧ{signx}
где Ŧ - оператор преобразования Фурье. Это позволило обеспечить вычисление фазы, согласно выражению (2).путем применения алгоритма быстрого преобразования Фурье.
В качестве итерационной процедуры был взят алгоритм сокращения ошибки /3/, как наиболее устойчивый и не зависящий от произвола исследователя в выборе параметров. Важно, что применение амплитудно-фазовых соотношений позволяет обрабатывать сигналы с высоким уровнем шума. Таким образом, общая схема процедуры была следующей /4/.
1. Вычислялось фазовое распределение 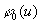 по известной величине амплитуды a(u) с помощью выражения (2); по известной величине амплитуды a(u) с помощью выражения (2);
2. Определялось начальное приближение изображения объекта для итерационной процедуры следующим образом:
ƒ0 (х)=Ŧ{a(u)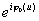 } }
- 18 -
Устанавливалось множество значений 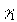 ={x}, расположенных внутри носителя. При этом носитель определялся теми значениями х=(х,у), для которых f0(х) повышала некоторое пороговое значение, которое в данной работе составляло около 0,1 от среднего значения Аср величины амплитуды, удовлетворяющей, в свою очередь условию А(х)≥0,1¸
0,2maх {f0(x)}. Такой подход позволил сократить влияние случайных шумов на формирование исходного приближения. Значения fо(x), оказавшиеся за пределом носителя, полагались равными нулю. Затем использовалась процедура алгоритма сокращения ошибки. ={x}, расположенных внутри носителя. При этом носитель определялся теми значениями х=(х,у), для которых f0(х) повышала некоторое пороговое значение, которое в данной работе составляло около 0,1 от среднего значения Аср величины амплитуды, удовлетворяющей, в свою очередь условию А(х)≥0,1¸
0,2maх {f0(x)}. Такой подход позволил сократить влияние случайных шумов на формирование исходного приближения. Значения fо(x), оказавшиеся за пределом носителя, полагались равными нулю. Затем использовалась процедура алгоритма сокращения ошибки.
Следует отметить, что если объект описывается достаточно гладкой функцией, то улучшение восстановленного с помощью амплитуднофазового соотношения изображения происходит очень медленно. Поэтому после определения носителя значения функции внутри него заполнялись случайными значениями, равномерно распределенными на интервале(0,1). При этом алгоритм фактически совпадал с процедурой Фьенапа /З/ с той лишь разницей, что носитель был неизвестен заранее.
В случае зашумленных данных ситуация совершенно иная. Шумоподобный характер сигнала приводит к тому, что заполнение носителя сразу же носит случайный характер. При этом небольшие изменения на каждом шаге итерации приводят к существенным изменениям наблюдаемой картины. Естественно, что реальной ситуации соответствует именно второй случай.
Здесь представлены результаты машинного моделирования качества восстановления изображения указанным алгоритмом при наличии шума. На рисунке 1 изображена зависимость величины среднеквадратичной ошибки восстановления от числа итераций при различном уровне аддитивного амплитудного шума. Параметр 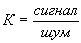 определяется отношением среднего значения амплитуды спектра модельного объекта к среднему значению шума. Влияние шума моделировалось путем добавления к амплитуде спектра |f(u)| случайной составляющей из соответствующего интервала (0,а) с равномерным законом распределения. определяется отношением среднего значения амплитуды спектра модельного объекта к среднему значению шума. Влияние шума моделировалось путем добавления к амплитуде спектра |f(u)| случайной составляющей из соответствующего интервала (0,а) с равномерным законом распределения.
Как видно из приведенных кривых, процедура достаточно быстро сходится при величине отношения сигнал/шум до 0,1. При
- 19 -
более высоком уровне шума сходимость мала. Однако задача еще может быть решена, если ввести предварительную фильтрацию для подавления высокочастотных флуктуации .
На рис.2 представлены результаты, отражающие зависимость уровня среднеквадратичной ошибки от числа итераций при наличии случайной фазовой модуляции объектного поля f(х). Для моделирования влияния шума рассматривалась функция
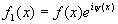
где 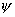 (х)=2 (х)=2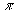 a, а принимает в каждой точке случайные значения равномерно из интервала ( a, а принимает в каждой точке случайные значения равномерно из интервала (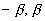 ). Данная модель соответствует диффузно рассеивающему объекту. Рисунок 3 отражает типичный пример восстановления изображения модельного объекта (рис.За) после применения соотношения (2) ( ). Данная модель соответствует диффузно рассеивающему объекту. Рисунок 3 отражает типичный пример восстановления изображения модельного объекта (рис.За) после применения соотношения (2) (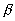 =0,6) и последующего выполнения 20 итераций - рис, 3б. Приведенные результаты свидетельствуют о высокой скорости сходимости рассматриваемой в данной работе процедуры. Узнаваемое восстановление достигалось после выполнения десятка итераций. =0,6) и последующего выполнения 20 итераций - рис, 3б. Приведенные результаты свидетельствуют о высокой скорости сходимости рассматриваемой в данной работе процедуры. Узнаваемое восстановление достигалось после выполнения десятка итераций.
Указанная функция f1(x) носит существенно комплексный характер. В последнее время в работах /7,8/ отмечалась возможность восстановления изображений подобных объектов. В /7/ однако для восстановления потребовалось выполнить свыше 1000 итераций при наличии точной информации о носителе. При этом показано, что небольшие погрешности в измерении его приводят к увеличению необходимого для достижения восстановления числа итераций в несколько раз. Носитель же, как правило, неизвестен. В /8/ удалось сократить количество итераций, требуемых для восстановления, не используя априорную информацию о носителе. При этом выбиралось начальное приближение заведомо близким к решению.
Приведем далее результаты обработки экспериментальных данных. В качестве исходного объекта служил транспарант цифры "2", расположенный в передней фокальной плоскости линзы и освещаемый плоской монохроматической волной. В качестве источника света служил гелио-неоновый лазер. Пространственный спектр объекта форсировался в задней фокальной плоскости линзы и регистрировался на фотопленку. Полученная дифракционная картина изображена на рис.4а. Результаты ее микрофотометрирования в виде массива данных размером
- 20 -
64х64 отсчета вводились в ЭВМ совместно с кривой почернения фотопленки. Как видно из приведенного рисунка, дифракционная картина не обладает центральной симметрией, что свидетельствует о том, что объектная функция f(x) является комплексной.
В силу высокого уровня зарегистрированных на пленке шумов в работе осуществлялась предварительная фильтрация указанного массива путем умножения его на весовую функцию. Следует отметить, что специальных исследований по выбору фильтра и оптимизации его параметров не проводилось. На рис.4б приведено изображение транспаранта, полученное путем применения описанной процедуры после выполнения 30 итераций. Общее время счета на ЭВМ ЕС-1060 составило ~1,5 мин.
Приведенные результаты свидетельствуют о возможности восстановления изображений объектов по амплитуде их пространственных спектров с помощью амплитудно-фазовых соотношений.
Л и т е р а т у р а
1. Обратные задачи в оптике.(Под ред.Г.П.Болтса). М. Машиностроение. 1984. 200с.
2. М.В.Клибанов. // Вопросы кибернетики. Автоматизированные системы ввода-вывода графической информации и их приложения. М. 1987. С. 6-i8.
3. fienup j.r. appl.opt., 1932. v.21, n.15. 2758-2769.
4. Г.Л.Акимова, Ю.П.Сырых, А.В.Фролов. Автометрия. 1988. №1. С. 85-88.
5. Л.И.Ронкин. Введение в теорию целых функций многих переменных. М. Наука. 1971. 432с.
6. П.Сырых, А.В.Фролов. // Физические явления в приборах электронной и лазерной техники. М. 1985. С. 71-74.
7. lane r.g. optica commun., 1987. v.63. n.1, 6-10.
8. В.П.Бакалов, К.М.Шитов. Известия ВУЗов. Радиоэлектроника. 1986. Т.29. №9. С.82-84.
- 21 -
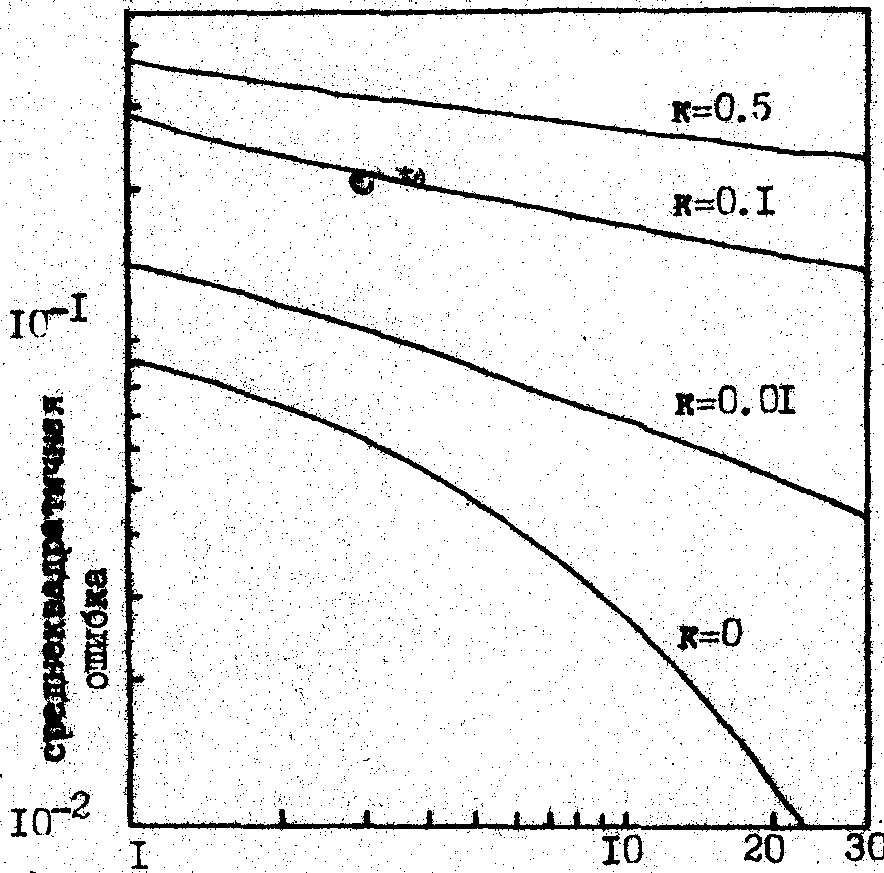
число итераций
Рис.1.
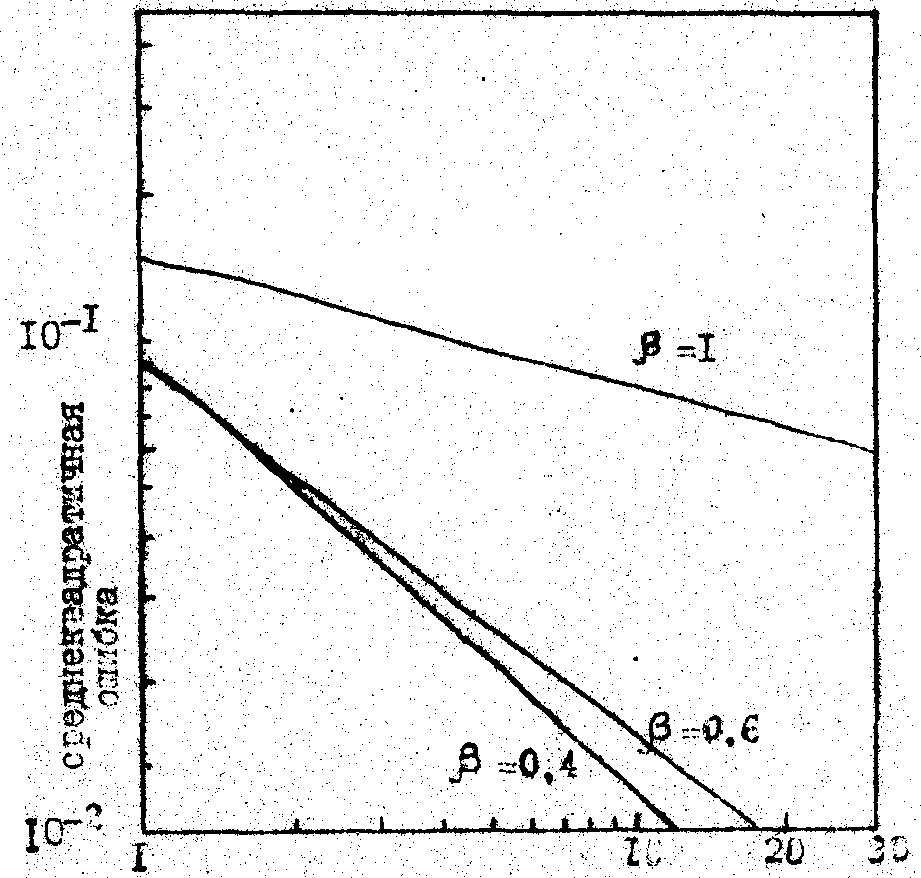
число итераций
Рис.2.
- 22 -
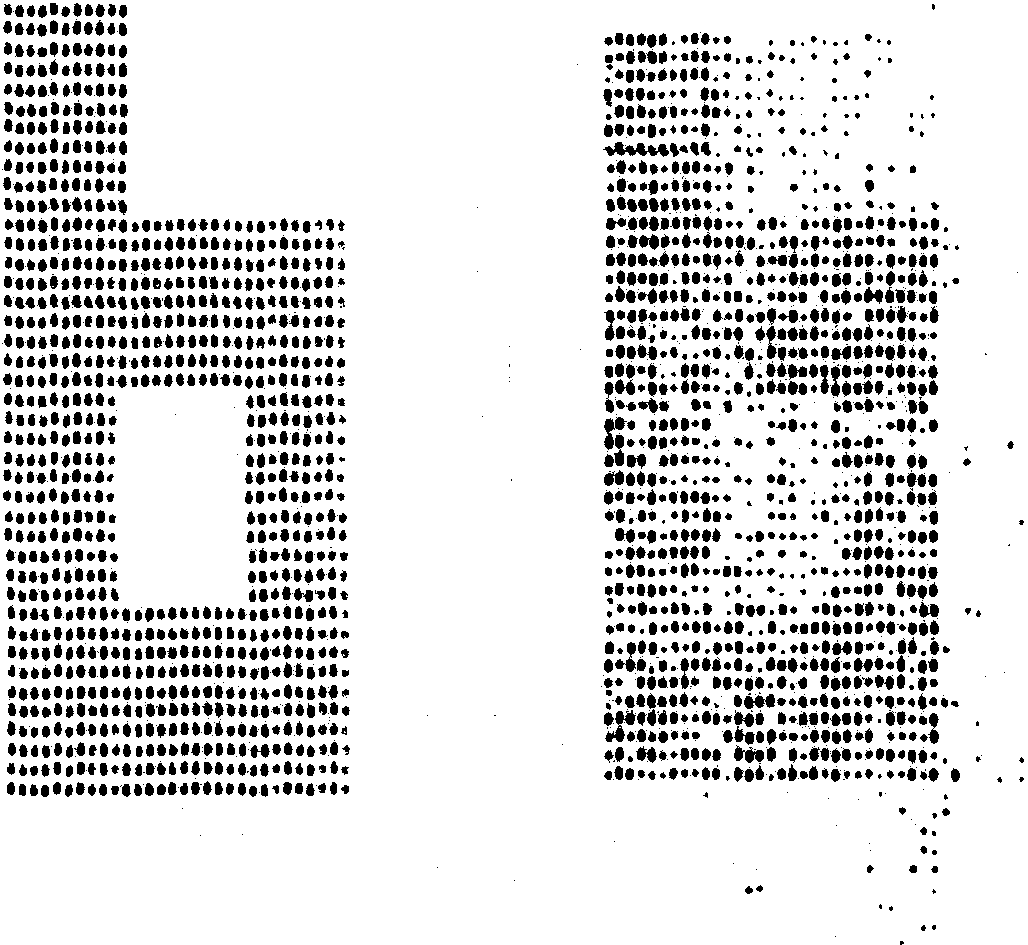
a) б)
Рис. 3

а) б)
Рис.4.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

