|
|
 |
 |

|
| |
ОПРВДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ И ДЕФОРМАЦИЙ
ПО НАЛОЖЕННЫММ НА ИССЛЕДУЕМУЮ ПОВЕРХНОСТЬ ГОЛОГРАММ
А.А.Рассоха
В данной работе предложены методики определения перемещения и деформаций по голограмме двойной экспозиции: освещением узким лучом лазера голограммы сфокусированного изображения и расшифровкой возникающей при этом на плоском непрозрачном экране интерференционной картины; регистрацией трех голографических интерферограмм и измерением расстояний между интерференционными полосами на них; изменением угла наблюдения голографической интерферограммы и измерением изменения расстояния между интерференционными полосами. Получены соответствующие соотношения между вектором перемещения и параметрами интерференционной картины на непрозрачном экране при освещении голограммы сфокусированного изображения узким лучом лазера, а также дифференциальные зависимости между деформациями и частотой интерференционных полос и ее изменением при изменении угла наблюдения восстановленного голографического изображения.
В последние года получить голограмму двойной экспозиции, характеризующую сложные поля перемещений и деформаций поверхности объекта исследования стало гораздо легче, чем провести по голограмме количественный анализ этих полей. Получение голограммы особенно сильно упрощается при использовании голографического способа определения деформаций /1/, в соответствии с которым голограмму
- 88 -
записывают по схеме Ю.Н.Денисюка со встречным опорным пучком на прозрачной фоточувствительной среде, наложенной на исследуемую поверхность и закрепленной на ней с помощью упругих податливых держателей или сред. В этом случае, как показали наши исследования, голограммы можно записывать без какой-либо виброзащиты, в производственных условиях, в условиях мощных вибраций. С помощью этого способа мы записывали голограммы объектов, которые перемещались во время экспозиции (или тем более между экспозициями) на несколько десятков сантиметров, вращались, совершая за время экспозиции тысячи оборотов, во время экспозиции держали лазер (ЛГ-79) в руках, голографируемый объект держали во время экспозиции в руках, между экспозициями высверливали электродрелью в детали отверстия, между экспозициями объект (с закрепленной на нем фотопластиной) переносили в соседний цех, обрабатывали и голографировали снова держа его в руках, а экспонирование производили без затемнения в условиях дневного и искусственного освещения.
Расшифровке голограмм, полученных этим способом, и посвящена данная работа,
Вначале сделаем несколько общих замечаний. Во-первых, рассматриваемые голограммы можно расшифровывать несколькими способами, производя оптическую фильтрацию как спекл-фотографии /2/, освещая узким лучом лазера, и, наконец, наблюдая полное голографическое изображение объекта с различных направлении.
Во-вторых, при освещении такой голограммы узким лучом лазера восстанавливаются две смещенные в пространстве спекл-структуры, и интерференцию формирующих эти спекл-структуры излучений можно наблюдать на непрозрачном экране, установленном на некотором расстоянии от голограммы. Поскольку спекл-структуры смещены в пространстве, то при произвольном положении экрана интерференционные полосы представляют собой линии пересечения семейства софокусных двухполостных гиперболоидов вращения с плоскостью экрана.
В-третьих, указанные голограммы позволяют наблюдать восстановленные изображения в большом телесном угле, что увеличивает точность вычислений, улучшая обусловленность разрешающей системы уравнений. Если освещать голограмму, наложенную на исследуемую поверхность, узким (нерасширенным) лучом лазера, то возникающая
- 89 -
в пространстве интерференционная картина описывается уравнениями семейства софокусных гиперболоидов:
4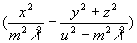 =1 (1) =1 (1)
где m - целое число (порядок), ось х декартовой системы координат Х, Y, Z совпадает с осью симметрии гиперболоидов, u - перемещение точки, изображение которой восстанавливает луч лазера, λ - длина волны излучения, начало координат расположено между фокусами семейства.
Выберем плоскость экрана
Ax+By+Cz=1 (2)
Опустим из начала координат перпендикуляр на плоскость (2). Точку пересечения перпендикуляра с плоскостью выберем за начало новой системы координат  такой, что всюду в плоскости (2) такой, что всюду в плоскости (2)  =0, т.е. направление оси =0, т.е. направление оси  будет совпадать с нормалью к плоскости. Для удобства рассмотрения направим ось Y так, чтобы перпендикуляр к плоскости (2) принадлежал плоскости хОу. Пусть также ось будет совпадать с нормалью к плоскости. Для удобства рассмотрения направим ось Y так, чтобы перпендикуляр к плоскости (2) принадлежал плоскости хОу. Пусть также ось 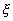 будет совпадать с осью Z, тогда связь между координатами xyz и будет совпадать с осью Z, тогда связь между координатами xyz и 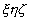 будет иметь вид: будет иметь вид:
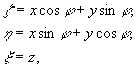 (3) (3)
где
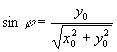 (4) (4)
a х 0 и у0 - координаты X и Y точки пересечения перпендикуляра к плоскости (2) с этой плоскостью.
Обозначая длину перпендикуляра (расстояние от голограммы
- 90 -
до экрана)
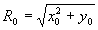 (5) (5)
после ряда преобразований получим уравнения сечений поверхностей (1) плоскостью (2);
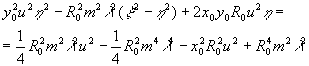 (6) (6)
Обозначая левую часть выражения (6) через Ф, дифференцируя Ф по координатам 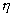 и и 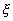 и составляя полный дифференциал Ф, который равен нулю, так как правая часть выражения (6) постоянная, получим и составляя полный дифференциал Ф, который равен нулю, так как правая часть выражения (6) постоянная, получим
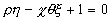 (7) (7)
где 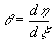 - тангенс угла наклона касательной к следу поверхности (1) на плоскости (2), - тангенс угла наклона касательной к следу поверхности (1) на плоскости (2),
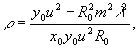 (8) (8)
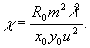 (9) (9)
Величины 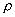 и и 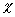 определяются как коэффициенты прямых (7), которые получаются при построении линий пересечения поверхностей (1) с плоскостью (2) в координатах определяются как коэффициенты прямых (7), которые получаются при построении линий пересечения поверхностей (1) с плоскостью (2) в координатах 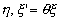 . .
Из соотношений (8) и (9) следует формула
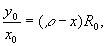 (10) (10)
- 91 -
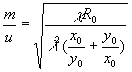 (11) (11)
Для определения межфокусного расстояния U необходимо знать величину m, которая по физическому смыслу является порядком интерференционной полосы. Однако в большинстве встречающихся на практике случаев порядок интерференционной полосы в эксперименте установить затруднительно. Поетому, учитывая, что на экране обычно наблюдается не одна, а несколько интерференционных полос, поступим следующим образом. С помощью соотношения (11) по t-ой линии пересечения поверхностей (1) с плоскостью (2) определяется величина
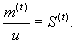 (12) (12)
С помощью соотношения (11) по (t+1)-ой смежной линии пересечения определяется величина
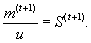 (13) (13)
где
m(t+1)=m±1 (14)
Из соотношений (12) и (13) следует формула для определения перемещений
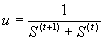 (15) (15)
Направление вектора перемещения определяется знаком в соответствии (14). Этот знак легко определяется из анализа уравнений линий пересечения (6) при различных значениях m. Как следует из этого анализа, средняя кривизна линии пересечения тем больше,
- 92 -
чем меньше величина m. Следовательно, если кривизна (t+1)-ой линии пересечения меньше, чем кривизна t-ой линии пересечения, то в формуле (14) следует взять знак плюс и направление вектора перемещения - по оси Х, в противном случае - знак минус и направление вектора перемещения - против оси Х.
Таким образом, рекомендуемый для расшифровки голограмм двойной экспозиции сфокусированного изображения с помощью узкого лазерного луча метод, соответствующий произвольному положению плоского экрана, заключается в том, что
1) для двух смежных интерференционных полос на плоском экране определяют величину 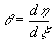
2) выполняют построение линий, соответствующие этим интерференционным полосам в координатах 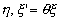 , в которых линии пересечения гиперболоидов с плоскостью - прямые (поэтому значение величины , в которых линии пересечения гиперболоидов с плоскостью - прямые (поэтому значение величины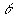 необходимо определять лишь в двух точках, лежащих на интерференционной полосе); необходимо определять лишь в двух точках, лежащих на интерференционной полосе);
3) определяют коэффициенты уравнений построенных прямых (7);
4) производят вычисления по формулам (10), (11) и (15);
4) сравнивая кривизны интерференционных полос определяют знак в формуле (14) и направление вектора перемещения. Положение оси X в пространстве определяется значением угла 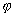 (4) и тем, что ось Х лежит в плоскости, проходящей через освещаемую точку на голограмме и ось симметрии интерференционной картины на экране. (4) и тем, что ось Х лежит в плоскости, проходящей через освещаемую точку на голограмме и ось симметрии интерференционной картины на экране.
Изложенная выше общая методика расшифровки значительно упрощается, если плоскость экрана занимает некоторые частные положения, в то время как до этого мы лишь направляли ось 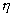 на экране так, чтобы она была осью симметрии интерференционной картины, а начало координат на экране так, чтобы она была осью симметрии интерференционной картины, а начало координат 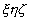 помещали в основании перпендикуляра к экрану, опущенного из освещаемой на голограмме точке. помещали в основании перпендикуляра к экрану, опущенного из освещаемой на голограмме точке.
Вначале рассмотрим случай, когда плоскость расположена параллельно вектору перемещения точки. В этом случае интерференционная картина на экране имеет две взаимно перпендикулярные оси симметрии, проходящие через точку X=О, у= R0.
Для рассматриваемого случая (х 0=0, у=R0, z=0} вдоль оси 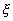 из соотношения (6) для m=1 следует формула из соотношения (6) для m=1 следует формула
- 93 -
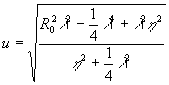 (16) (16)
где 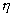 - расстояние на плоскости между интерференционными полосами m=О, m=1, т.е. между прямой интерференционной полосой (m=0) и ближайшей к ней (m=1). При - расстояние на плоскости между интерференционными полосами m=О, m=1, т.е. между прямой интерференционной полосой (m=0) и ближайшей к ней (m=1). При 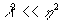 и и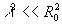 из выражения (16) следует из выражения (16) следует
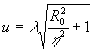 (17) (17)
Если 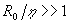 , что бывает далеко не всегда, то из формулы (17) следует , что бывает далеко не всегда, то из формулы (17) следует
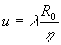 (18) (18)
что совпадает с известной формулой для определения перемещений по спекл-интерферограммам при просвечивании спекл-фотографий двойной экспозиции узким лучом лазерного излучения.
На практике, чтобы воспользоваться формулой (17), достаточно расположить плоский экран так, чтобы он содержал прямую интерференционную полосу и был перпендикулярен прямой, проведенной через эту интерференционную полосу и точку на голограмме, которая освещает узкий луч лазера. Заметим здесь, что освещение голограммы узким лучом лазера необходимо проводить в направлении опорного пучка при записи голограммы.
В некоторых случаях интерференционная картина восстанавливается при освещении голограммы узким лучом в неполном телесном угле и на плоском экране имеет вид концентрических окружностей. Заметим также, что на сферическом экране с центром в освещаемой узким лучом точке голограммы интерференционные полосы всегда являются окружностями.
Рассмотрим соответствующий случай расположения плоского экрана
- 94 -
когда он перпендикулярен оси симметрии семейства софокусных гиперболоидов и расположен на расстоянии Х 0=R 0 от начала координат Х, У, Z. Для рассматриваемого случая уравнения линий пересечения (6) принимают вид (при Х0=R 0, У0=0}:
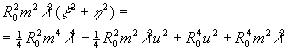 (19) (19)
Если 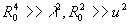 то из выражения (19) следует то из выражения (19) следует
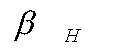 (20) (20)
Записывая соотношение (20) для двух смежных порядков m и m+1 и обозначая 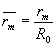 , где rm - радиус кривизны интерференционной полосы порядка m, имеем , где rm - радиус кривизны интерференционной полосы порядка m, имеем
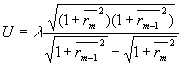 (21) (21)
Для случая 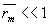 из выражения (21) следует из выражения (21) следует
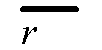 (22) (22)
где 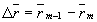
Если на экране в центре окружностей наблюдается светящаяся точка, то вместо соотношения (22) необходимо использовать соотношение
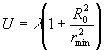 (23) (23)
где 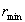 -радиус наименьшей окружности на экране. -радиус наименьшей окружности на экране.
Рассмотрим несколько более общий случай. Пусть два полюса 1 и 2 (рис.1) гиперболоидов (1) дают на плоскости экрана следы в виде кривых второго порядка, проходящих через точки 3,4 и 5.
- 95 -
Расстояние между точками 1 и 2 имеет физический смысл перемещения точки, которую освещает узкий луч лазера на голограмме сфокусированного изображения. Обозначим расстояния между точками З и 4 – b1, 3 и 5 – b2, 0 и 3 – R0. Введем такие углы 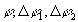 , показанные на рис.1: , показанные на рис.1:
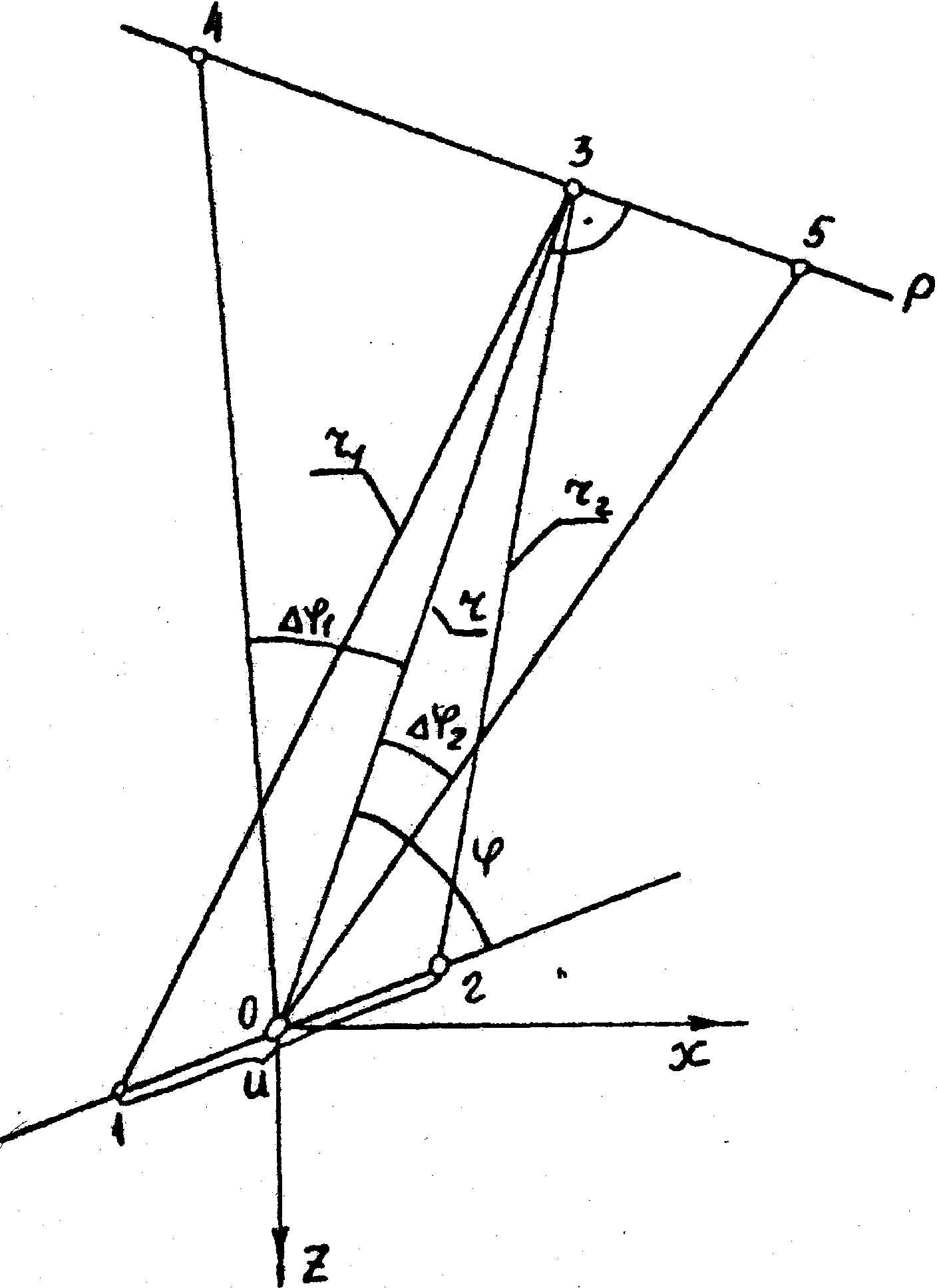
Рис.1.
- 96 -
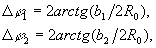 (24) (24)
Из соотношения (1) для точек 3, 4 и 5 следует
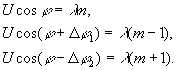 (25) (25)
Откуда после преобразований получаем
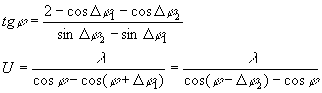 (26) (26)
Таким образом, по расстоянию между интерференционными полосами на экране b1 и b2 с помощью соотношения (26) определяется величина перемещения - угол между прямой 0-3 (направлением от освещаемой точки голограммы к основанию перпендикуляра, опущенного из этой точки на плоскость экрана) и вектором перемещения.
Для определения направления вектора перемещения в пространстве введем некоторый единичный вектор 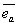 в этом направлении, такой, что в этом направлении, такой, что
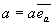 , (27) , (27)
где
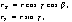 , (28) , (28)
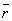
- вектор, соединяющий тонки 0 и 3 (рис.2), - единичный вектор
- 97 -
в направлении, перпендикулярном интерференционным полосам на экране (рис.2).
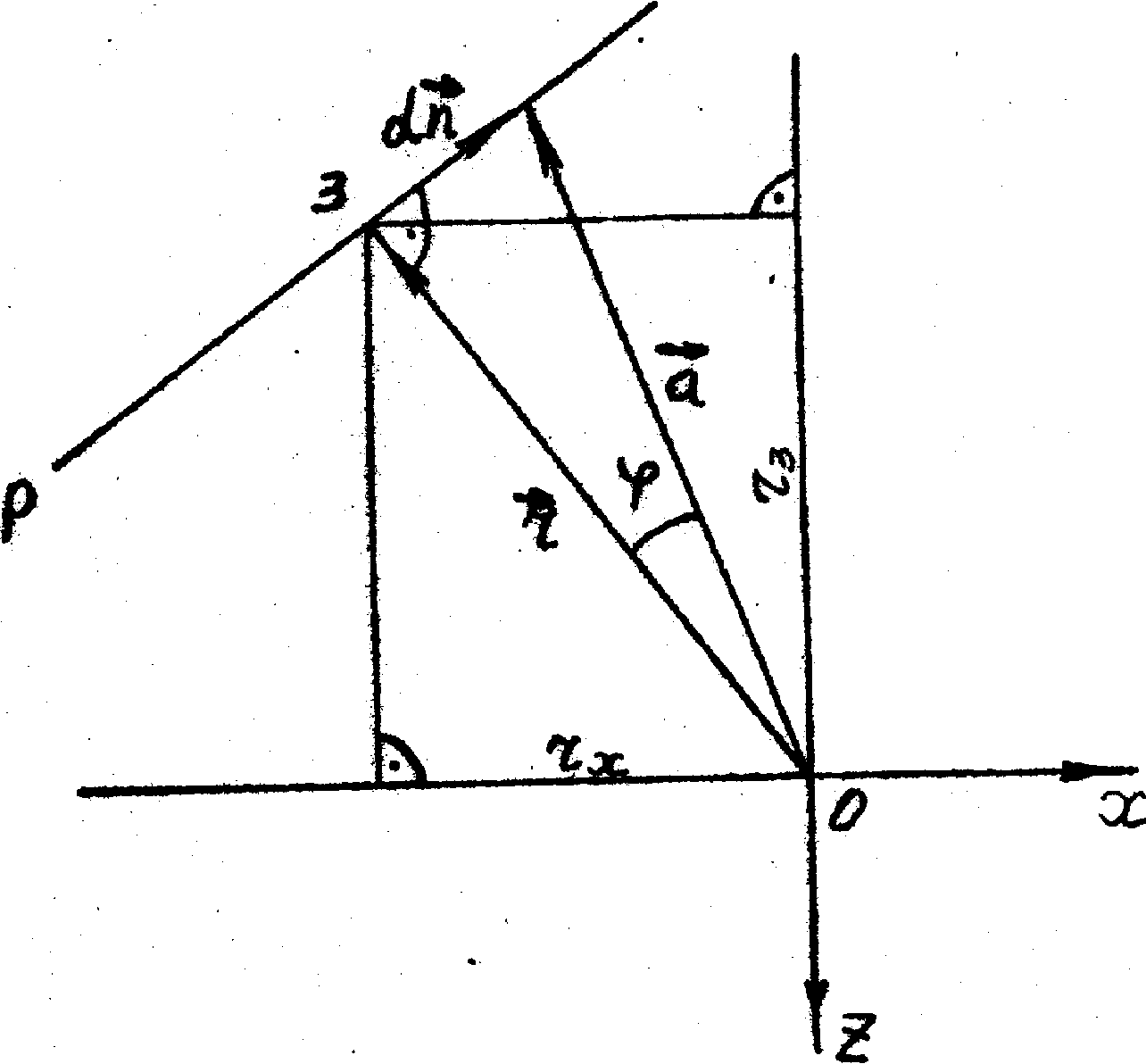
Рис.2.
Введем также систему декартовых координат X, Y, Z, начало которой поместим в точке 0 (рис.2), и систему координат X', Y', Z', начало которой поместим в точке 3, а оси Х', Y' - в плоскости экрана (рис.2), перпендикулярной вектору 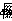 на рис.2, т.е. линии 0-3 на рис,1. Направим ось Y' параллельно оси Y, обозначив угол между вектором на рис.2, т.е. линии 0-3 на рис,1. Направим ось Y' параллельно оси Y, обозначив угол между вектором 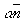 , лежащим в плоскости экрана, и осью X' через , лежащим в плоскости экрана, и осью X' через 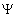 (рис.3). Тогда из рис.2 имеем (рис.3). Тогда из рис.2 имеем
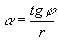 (29) (29)
а из рис.3 имеем
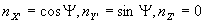 (30) (30)
Компоненты единичного вектора 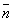 находятся по формулам: находятся по формулам:
- 98 -
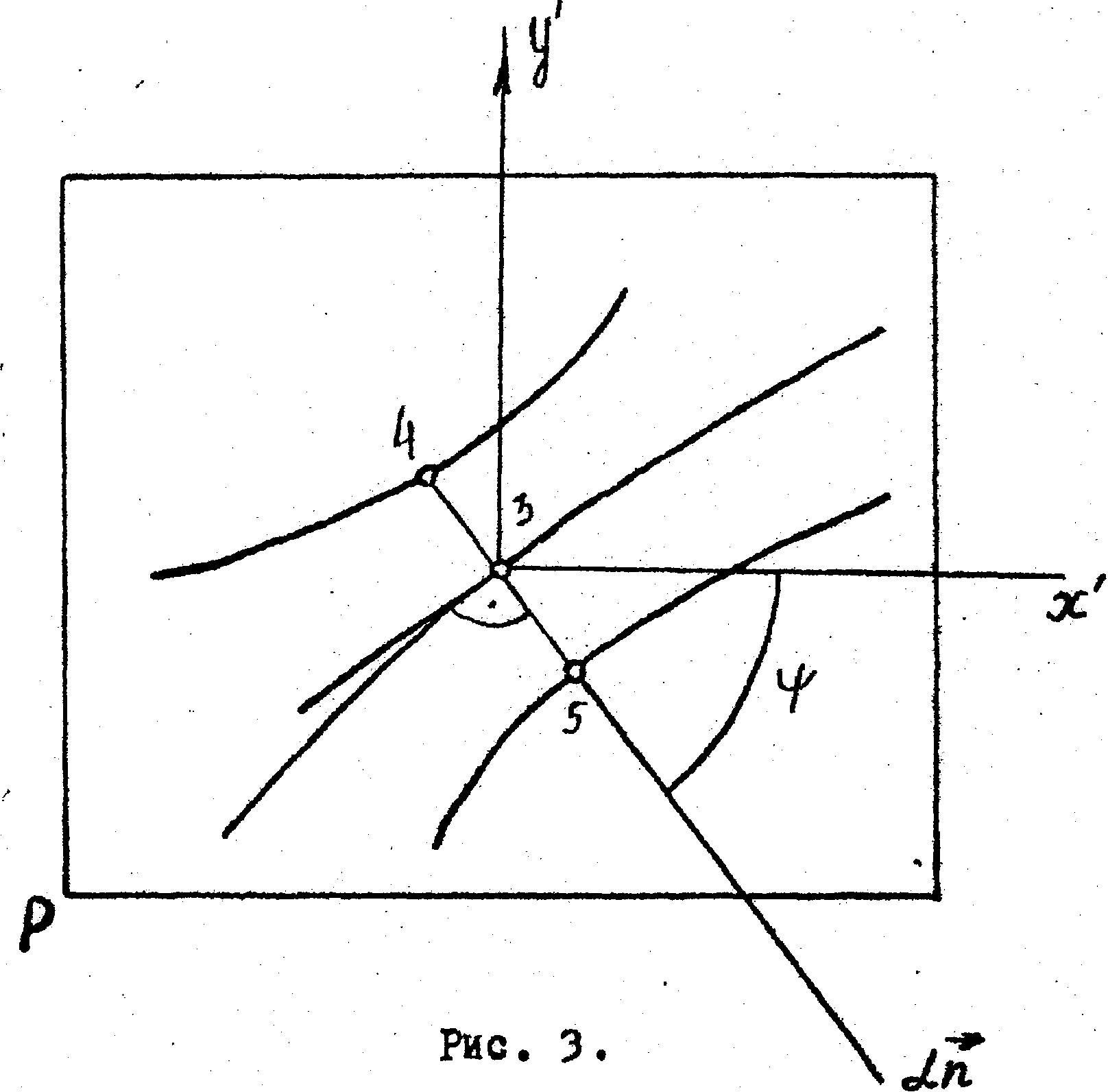
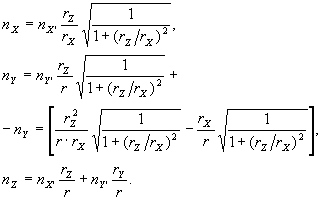 (31) (31)
- 99 -
Направляющие косинусы единичного вектора в направлении перемещения определяются соотношениями:
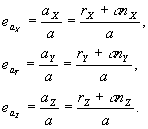 (32) (32)
где 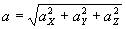 . .
Величины rX и rY можно либо непосредственно измерять при просвечивании голограммы лучом лазера, либо вычислять по экспериментально определяемым углам β и γ (рис.4) с помощью формул:
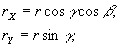 (33) (33)
а величину rZ определять по формуле:
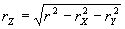 (34) (34)
Заметим, что полученные выше соотношения можно использовать также для расшифровки голограмм, когда в область действительного голографического изображения помещается экран с отверстием.
Наконец, рассмотрим расшифровку голограмм, наложенных на исследуемую поверхность, при освещении ее широким пучком коллимированного света. В принципе, изложенное ниже справедливо и для расшифровки классических голограмм двойной экспозиции как с наклонным, так и со встречный опорным пучком.
- 100 -
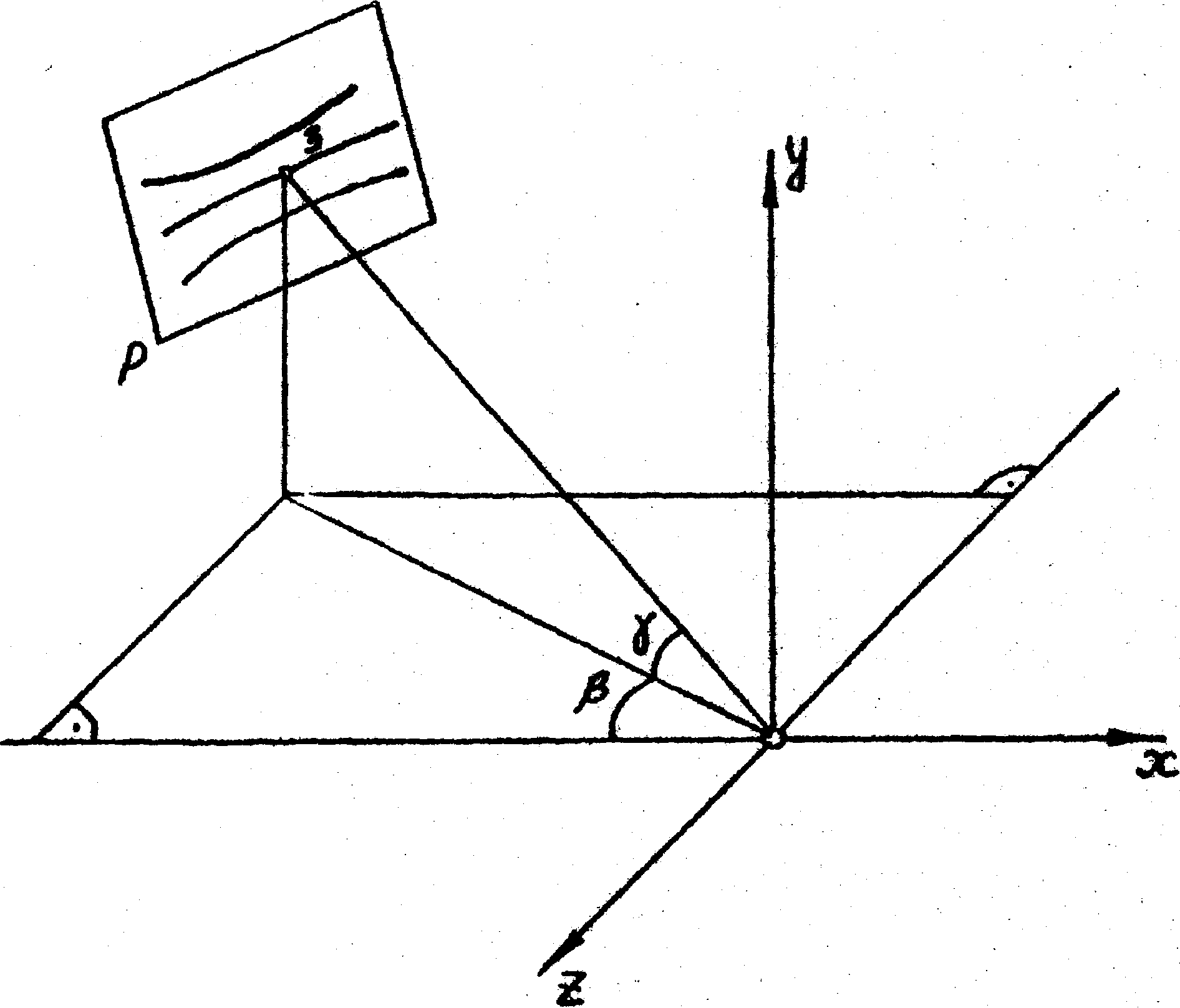
Рис .4.
- 101 -
Однако, расшифровка голограмм, наложенных на исследуемую поверхность, имеет ряд преимуществ, основным из которых является то, что восстановленное такими голограммами изображение наблюдается в большом телесном угле, что улучшает обусловленность разрешающей системы уравнений для составляющих вектора перемещения или тензора деформаций, что уменьшает зависимость результатов от ошибок измерения параметров интерференционных картин.
Запишем соотношение (1) для двух точек исследуемой поверхности, через которые проходят две соседние интерференционные полосы, порядки которых - смежные целые числа m и m+1. Пусть координаты первой точки будут X, Y, Z, а второй X+ΔX, Y+ΔY, Z+ΔZ. Тогда:
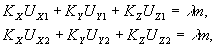 (35) (35)
где 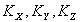 - проекции вектора, равного сумме двух единичных векторов - в направлении освещения и наблюдения исследуемой поверхности, - проекции вектора, равного сумме двух единичных векторов - в направлении освещения и наблюдения исследуемой поверхности,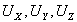 - проекции вектора перемещения. - проекции вектора перемещения.
Вычтем первое уравнение (35) из второго и разделим результат последовательно на ΔХ и Δ Y:
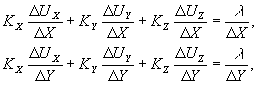 (36) (36)
где 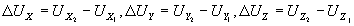
При неограниченном уменьшении расстояния между линиями пересечения поверхностей, т.е. при уменьшении расстояния между интерференционными полосами, формально возможен предельный переход в соотношениях (36):
- 102 -
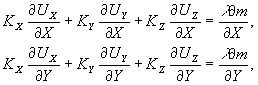 (37) (37)
Для определения всех неизвестных производных перемещений необходимо наблюдать голографическую интерферограмму с трех различных направлений, не лежащих в одной плоскости, и решить систему уравнений:
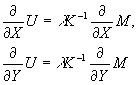 (38) (38)
где
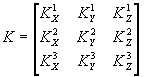
(39)
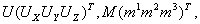
а верхний индекс соответствует одному из направлений наблюдения.
В ряде случаев вместо соотношения (38) удобнее пользоваться формулами, которые получим из соотношении (38), продифференцировав уравнения (38) по KX и KY:
- 103 -
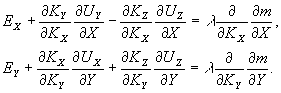 (40) (40)
Введем углы 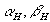 и и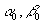 , определяющие направление наблюдения и освещения исследуемой поверхности: , определяющие направление наблюдения и освещения исследуемой поверхности:
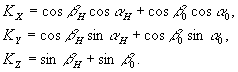 (41) (41)
Пользуясь соотношениями (41), найдем производные
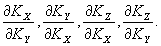
Например, для 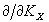 имеем имеем
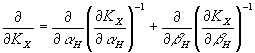 (42) (42)
которое при постоянной величине угла 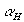 приобретает вид: приобретает вид:
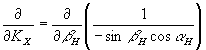 (43) (43)
При 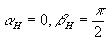 ,т.е. при освещении и наблюдении голографической интерферограммы по нормали к поверхности, имеем из выражения (43): ,т.е. при освещении и наблюдении голографической интерферограммы по нормали к поверхности, имеем из выражения (43):
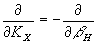 (44) (44)
- 104 -
Аналогично можно найти выражения для производных 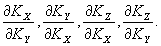 при других значениях при других значениях 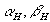 , ,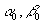 . С учетом этих соотношений формулы, найденные из выражений (40) для компонент тензора линейных деформаций и производных, определяющих сдвиговые деформации для некоторых значений углов, имеют вид: . С учетом этих соотношений формулы, найденные из выражений (40) для компонент тензора линейных деформаций и производных, определяющих сдвиговые деформации для некоторых значений углов, имеют вид:
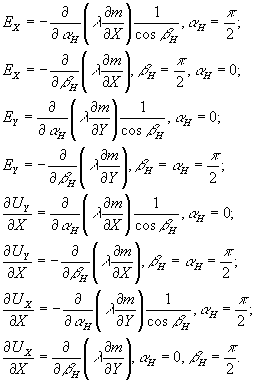 (45) (45)
- 106 -
Соотношения (45) позволяют определять линейные и сдвиговые деформации либо при изменении угла между нормалью к поверхности и направлением наблюдения ( 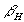 ), либо при изменении угла ), либо при изменении угла 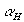 между осью Х и проекцией поправления наблюдения на плоскость хОу при постоянном между осью Х и проекцией поправления наблюдения на плоскость хОу при постоянном 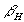 . .
Приближенно величину производных межфокусного расстояния с помощью соотношений (45) можно вычислить, например, так. Наблюдая голографическое изображение с какого-либо направления, характеризуемого углами 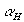 , ,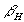 , изменим величину , изменим величину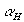 или или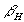 на небольшую конечную величину, измерим изменение расстояния между интерференционными полосами и вычислим искомые производные, переходя в соотношениях (45) к конечным разностям. Например, если направление освещения и наблюдения совпадает с нормалью к исследуемой поверхности, то, чтобы определить деформацию в каком-либо направлении, достаточно изменить направление наблюдения так, чтобы оно лежало в плоскости, включающей направление, в котором определяется линейная деформация. на небольшую конечную величину, измерим изменение расстояния между интерференционными полосами и вычислим искомые производные, переходя в соотношениях (45) к конечным разностям. Например, если направление освещения и наблюдения совпадает с нормалью к исследуемой поверхности, то, чтобы определить деформацию в каком-либо направлении, достаточно изменить направление наблюдения так, чтобы оно лежало в плоскости, включающей направление, в котором определяется линейная деформация.
В заключение заметим, что из полученных здесь формул для деформаций (45) следует важный вывод: если направление освещения и наблюдения совпадает с нормалью к исследуемой поверхности, то линейная деформация по касательной к интерференционной полосе всюду равна нулю, так как производная порядка интерференционной полосы по криволинейной координате вдоль интерференционной полосы равна нулю. Поэтому удобно пользоваться соотношениями, которые следуют из формул (45) с учетом этого вывода в координатах 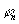 ( (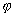 - по касательной, n- по нормали к интерференционной полосе): - по касательной, n- по нормали к интерференционной полосе):
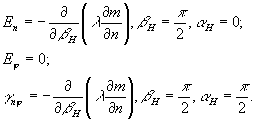 (46) (46)
- 106 -
Таким образом, для определения всех деформаций необходимо определить изменение расстояния между интерференционными полюсами при изменении направления наблюдения от нормального к поверхности в плоскости 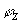 , включающей нормаль к поверхности и касательную к интерференционной полосе (первая формула (46)), и в плоскости nZ, включающей нормаль к исследуемой поверхности и нормаль к интерференционной полосе. , включающей нормаль к поверхности и касательную к интерференционной полосе (первая формула (46)), и в плоскости nZ, включающей нормаль к исследуемой поверхности и нормаль к интерференционной полосе.
Л и т е р а т у р а
1. Бакулин В.Н., Рассоха А. А, Метод конечных элементов и голографическая интерферометрия в задачах механики композитов. М., Машиностроение, 1987, с.271,
2. Клименко И.С. Голография сфокусированных изображений и спекл-интерферометрия. М., Наука. 1985, с,222.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

