|
|
 |
 |

|
| |
ЯВЛЕНИЕ САМОРЕПРОДУКЦИИ (ЭФФЕКТ ТАЛБОТА)
В ГОЛОГРАФИИ
А. Марипов
Приведены результаты теоретического и экспериментального исследования эффекта Талбота в голографии. Показано, что при освещении монохроматическим светом отбеленной голограммы периодических объектов, записанных по внеосевой схеме, в области действительного изображения одновременно восстанавливаются саморепродукции решетки не только в лучах ±
I порядков, но и в нулевом порядке дифракции.
В голографии эффект Талбота изучен еще слабо. В работах /1,2/ экспериментально проверена возможность саморепродукции периодической решетки с ее голограммы. В этих экспериментах голограммы одномерной решетки записывались по внеосевой схеме. При этом плоскость голограммы точно совпадала с одной из плоскостей саморепродукции. Последнее контролировалось с помощью вращающегося в плоскости голограммы матового стекла и наведенного на него микроскопа увеличением 100х. В /2/, в отличие от /1/, изучена саморепродукция периодической решетки с ее голограммы не только в области мнимого, но также и в области действительного изображения. Для этого в схему записи и восстановления голограммы вводится второй опорный пучок, сопряженный первому. Голограммы периодической решетки записывались на фотопластинку и обрабатывались на месте. Такие голограммы освещались исходными опорными пучками. Поскольку интенсивность восстановленных изображений была очень слабой, измеренный сигнал усиливался с помощью опто-электронного преобразователя в I000 раз и записывался на фотопленку. Найденные таким образом
- 41 –
положения саморепродукций решетки, восстановленных с голограммы в областях мнимого и действительного изображения, сравнивались с положениями плоскостей саморепродукций самой решетки, измерения показали равенства периодов саморепродукций самой решетки, восстановленных с голограммы и найденных теоретически.
Здесь приведены результаты теоретического и экспериментального исследований эффекта Талбота в голографии в более общем случае. Голограммы периодической решетки записываются по обычной внеосевой схеме, но, в отличие от /1,2/, расстояние от объекта до плоскости голограммы произвольное. Обнаружено, что саморепродукция решетки восстанавливается одновременно в области действительного изображения не только в ±
1 порядках, но и в направлении нулевого порядка дифракции.
Рассмотрим запись голограммы одномерной амплитудной решетки при произвольном ее расположении относительно плоскости голограммы 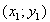 с помощью плоских волн - предметной с помощью плоских волн - предметной 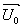 и опорной и опорной 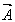 , соответственно, падающих под углом θ к оси и перпендикулярно к плоскости голограммы. Коэффициент пропускания такой решетки с прозрачностью щелей и промежутков равными, соответственно, 1 и 0 можно представить /3/ , соответственно, падающих под углом θ к оси и перпендикулярно к плоскости голограммы. Коэффициент пропускания такой решетки с прозрачностью щелей и промежутков равными, соответственно, 1 и 0 можно представить /3/
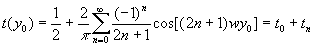
где - постоянная составляющая коэффициента пропускания, - дифракционная составляющая с ненулевой пространственной частотой, , d - период решетки в единицах длины. На некотором расстоянии от решетки предметная волна определяется выражением:
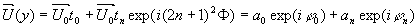
где а = U0t0, an = U0tn, 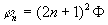 , , 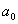 и и 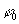 - амплитуда и фаза когерентного фона, - амплитуда и фаза когерентного фона, 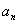 и и 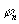 - амплитуда и фаза дифрагированных волн, а непосредственно за решеткой она равна - амплитуда и фаза дифрагированных волн, а непосредственно за решеткой она равна
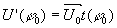
- 42 -
Интенсивность света, падающего на фотопластинку, определяется уравнением 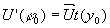
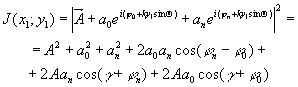 (3) (3)
где 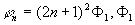 - фаза предметной волны, зарегистрированной на голограмме, - фаза предметной волны, зарегистрированной на голограмме, 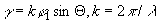 . В этом выражении имеется три интерференционных члена: первый член . В этом выражении имеется три интерференционных члена: первый член 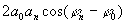 описывает голограммы Габора; второй член описывает голограммы Габора; второй член 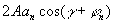 соответствует голограмме Френеля; третий член соответствует голограмме Френеля; третий член 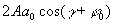 представляет собой интерференционную картину параллельных линий (одномерную периодическую решетку), локализованных на самой голограмме с пространственной частотой представляет собой интерференционную картину параллельных линий (одномерную периодическую решетку), локализованных на самой голограмме с пространственной частотой 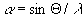 . В случае комбинаций сферических и плоских фронтов предметной волны такая интерференционная картина представляет собой зонную решетку Френеля. Она одновременно является положительной и отрицательной линзой. При выполнении условия линейности регистрации и обработки голограммы ее коэффициент пропускания . В случае комбинаций сферических и плоских фронтов предметной волны такая интерференционная картина представляет собой зонную решетку Френеля. Она одновременно является положительной и отрицательной линзой. При выполнении условия линейности регистрации и обработки голограммы ее коэффициент пропускания 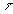 пропорционален пропорционален 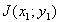 , то есть выражение (3) с точностью до постоянного множителя описывает функцию амплитудного пропускания голограммы объекта , то есть выражение (3) с точностью до постоянного множителя описывает функцию амплитудного пропускания голограммы объекта
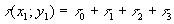
где
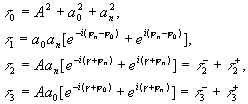 . .
- 43 -
Такая голограмма отбеливается. При этом фоновые 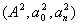 изображения устраняются, амплитуды интерференционных членов изображения устраняются, амплитуды интерференционных членов 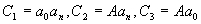 принимают постоянные значения по всей плоскости голограммы. принимают постоянные значения по всей плоскости голограммы.
Рассмотрим процесс восстановления такой голограммы. При освещении ее исходным опорным пучком  , волна за голограммой H распределяется по трем направлениям - прямом и под углами , волна за голограммой H распределяется по трем направлениям - прямом и под углами 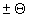 (рис.1). Волна, идущая в прямом направлении, равна (рис.1). Волна, идущая в прямом направлении, равна 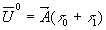 , а ее интенсивность будет определяться формулой , а ее интенсивность будет определяться формулой
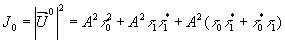 (4) (4)
где знак (*) означает комплексно сопряженную величину. Первый
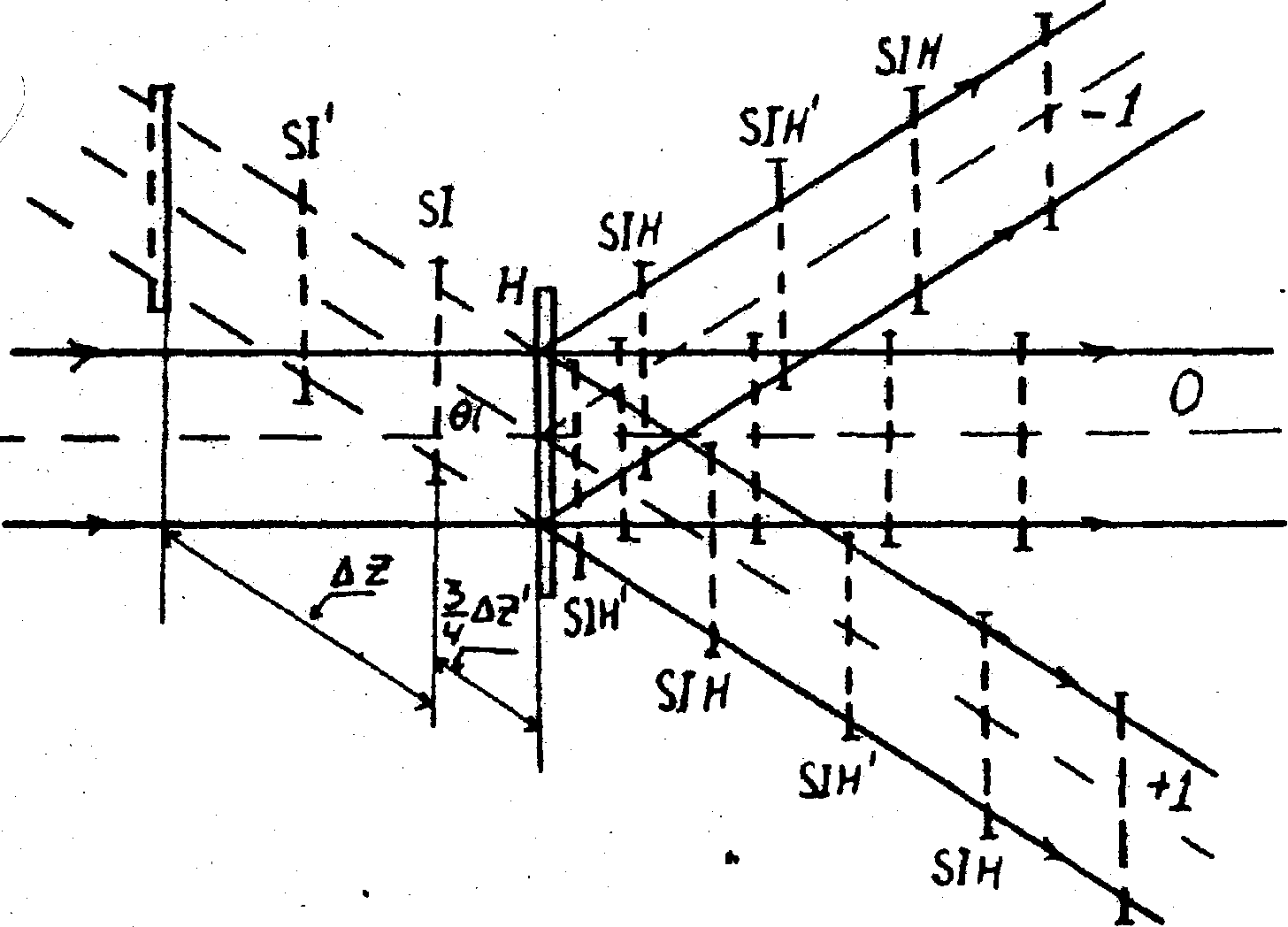
Рис.1. Оптическая схема записи голограммы.
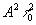
и второй 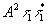 члены описывают фон, а третий член члены описывают фон, а третий член 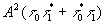 определяет восстановленные мнимое и действительное изображения объекта, как в голограмме Габора. Интенсивность полей в направлении 1 порядка дифракции соответственно, равна: определяет восстановленные мнимое и действительное изображения объекта, как в голограмме Габора. Интенсивность полей в направлении 1 порядка дифракции соответственно, равна:
- 44 -
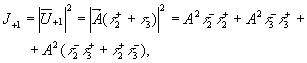 (5) (5)
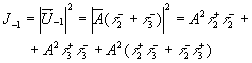 (6) (6)
В выражениях (5,6) компоненты 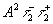 описывают обычные мнимое и действительное изображения объекта, восстановленные, соответственно, в ±
1 порядках дифракции. Компоненты описывают обычные мнимое и действительное изображения объекта, восстановленные, соответственно, в ±
1 порядках дифракции. Компоненты 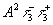 описывают зонную решетку Френеля, локализованную на самой голограмме. Вследствие этого при освещении такой голограммы белым светом на самой голограмме восстанавливается радужное изображение объекта. описывают зонную решетку Френеля, локализованную на самой голограмме. Вследствие этого при освещении такой голограммы белым светом на самой голограмме восстанавливается радужное изображение объекта.
Отдельно рассмотрим компоненты 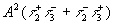 в выражениях (5) и (6), ответственные за возникновение эффекта Талбота. Определим положения плоскостей саморепродукции решетки в направлении ±
1 порядков: в выражениях (5) и (6), ответственные за возникновение эффекта Талбота. Определим положения плоскостей саморепродукции решетки в направлении ±
1 порядков:
В направлении +1 порядка изображение решетки описывается компонентом
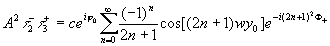 (7) (7)
где 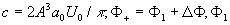 - состояние фазы предметной волны, записанной на голограмме, определяемой формулой (5), - состояние фазы предметной волны, записанной на голограмме, определяемой формулой (5), 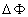 - изменение фазы восстановленной волны относительно голограммы. Знак (-) в экспоненте указывает на перенос мнимого изображения в действительную область пространства. - изменение фазы восстановленной волны относительно голограммы. Знак (-) в экспоненте указывает на перенос мнимого изображения в действительную область пространства.
- 45 -
Аналогично изображение решетки, переносимое в направлении I порядка, описывается компонентом интенсивности
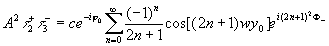 ,(8) ,(8)
где 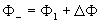
В плоскостях, удовлетворяющих условиям 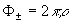 выражения (7) и (8), с точностью до постоянных множителей, будут совпадать с выражения (7) и (8), с точностью до постоянных множителей, будут совпадать с 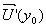 ,описывающим изображения решетки непосредственно за ней. При этом фаза восстановленных волн отсчитывается относительно голограммы с учетом состояния фазы предметной волны, зарегистрированной в голограмме. Следовательно, положения плоскостей саморепродукции решетки за голограммой зависят от относительного положения объекта и голограммы при ее записи, а также от направления дифрагированного луча, куда переносятся изображения решетки. Изменение фазы волны на ,описывающим изображения решетки непосредственно за ней. При этом фаза восстановленных волн отсчитывается относительно голограммы с учетом состояния фазы предметной волны, зарегистрированной в голограмме. Следовательно, положения плоскостей саморепродукции решетки за голограммой зависят от относительного положения объекта и голограммы при ее записи, а также от направления дифрагированного луча, куда переносятся изображения решетки. Изменение фазы волны на 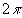 равносильно прохождению ею расстояния, равного периоду саморепродукции ΔZ. равносильно прохождению ею расстояния, равного периоду саморепродукции ΔZ.
Эксперименты проводились с одномерной амплитудной решеткой периодом d = 500 7 мкм, изготовленной фотографическим способом. При этом период саморепродукции решетки, согласно формуле равен ΔZ = 79,2 см (λ = 0,63 мкм). При записи голограммы, в отличие от /2/, расстояние Z1 между решеткой и плоскостью голограммы было произвольным. Полученные голограммы освещались плоской монохроматической волной, падающей нормально и голограмме (рис.1). При этом, кроме традиционных действительного и мнимого изображений решетки (на рисунках не показаны), на определенных расстояниях соответствующих +1 и -1 порядкам дифракции, одновременно
- 46 -
временно восстанавливались саморепродукции решетки у наблюдаемые на экранах, помещенных на пути этих волн. Эффект Талбота наблюдался также в прямом направлении на сильном фоне волны нулевого порядка. На рисунке положения плоскостей саморепродукции, позитивных и негативных изображений самой решетки обозначены через SI и SI’, а восстановленные с голограммы - через SIH и SIH’ соответственно (О’ - положения объекта при записи голограммы). Рис.1. соответствует условию записи
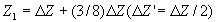 . .
При этом положения плоскостей саморепродукции выражались как
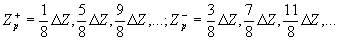
Отсюда следует, что положения плоскостей саморепродукции в разных направлениях неодинаковы, первое восстановленное изображение в направлении -1 порядка позитивное, а в направлении +1 порядка оно негативное, далее чередуются позитивное с негативным и наоборот. Пространственные спектры восстановленных изображений решетки

- 47 -
в направлениях +1, О, -1 порядков дифракции показана, соответственно, на рис.2. Эти спектры получены по схеме Аббе /З/.
Таким образом, экспериментально подтверждено, что при освещении монохроматическим светом отбеленной голограммы периодической решетки одновременно восстанавливаются саморепродукции решетки не только в лучах ±1 порядка, но и в нулевом порядке дифракции.
Литература
1. Konitz H - Optik, 1984, v 66, №3, p.197 – 204.
2. Konitz H - Optik, 1985, v 69, №3, p.91 - 93.
3. Борн М., Вольф Э. Основы оптики. М., "Наука", 1970, с. 855.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

