|
|
 |
 |

|
| |
устойчивость алгоритма восстановления фазы
ПО НАБОРУ ИЗОБРАЖЕНИЙ
В.П.Сивоконь
Задача восстановления фазы световой волны в некоторой плоскости по распределению интенсивности, зарегистрированному в другой плоскости” известна как фазовая проблема в оптике / I-3/.
Рис.1 иллюстрирует одну из типичных постановок этой задачи. На вход Z=O, некоторой оптической системы (например, линзы) падает световая волна, комплексная амплитуда поля которой имеет вид:
А(  )=А0 )=А0(  )*exp(iU(  )), (1)
где  ={x,y} декартовы координаты в плоскости, перпендикулярной оси распространения 0Z, А02 ={x,y} декартовы координаты в плоскости, перпендикулярной оси распространения 0Z, А02(  ) – интенсивность волны на входе системы, a U( ) - подлежащая определению фаза. В выходной плоскости системы Z=Z0 регистрируется распределение интенсивности I0( ) - подлежащая определению фаза. В выходной плоскости системы Z=Z0 регистрируется распределение интенсивности I0( )=│Â( )=│Â( ,Z=Z0)│2, которое в дальнейшем будем называть "изображением". Поле изображения Â( ,Z=Z0)│2, которое в дальнейшем будем называть "изображением". Поле изображения Â( ) связано с входным полем А( ) связано с входным полем А( ) некоторым преобразованием (Фурье, если Z0=F - -фокусу линзы, Френеля, если Z0≠F). ) некоторым преобразованием (Фурье, если Z0=F - -фокусу линзы, Френеля, если Z0≠F).
Задача состоит в том, чтобы по известным распределениям интенсивностей А 02 и I0 определить неизвестную фазу поля U( ) )
Как и большинство обратных задач, поставленная задача восстановления фазы является, вообще говоря, некорректной. Поэтому особое внимание уделяют исследованию единственности и устойчивости ее решения. Проблема единственности является достаточно сложной и к настоящему времени не подучила всего исчерпывающего решения /I-5/, хотя в последних работах и был достигнут заметный
- 17 -
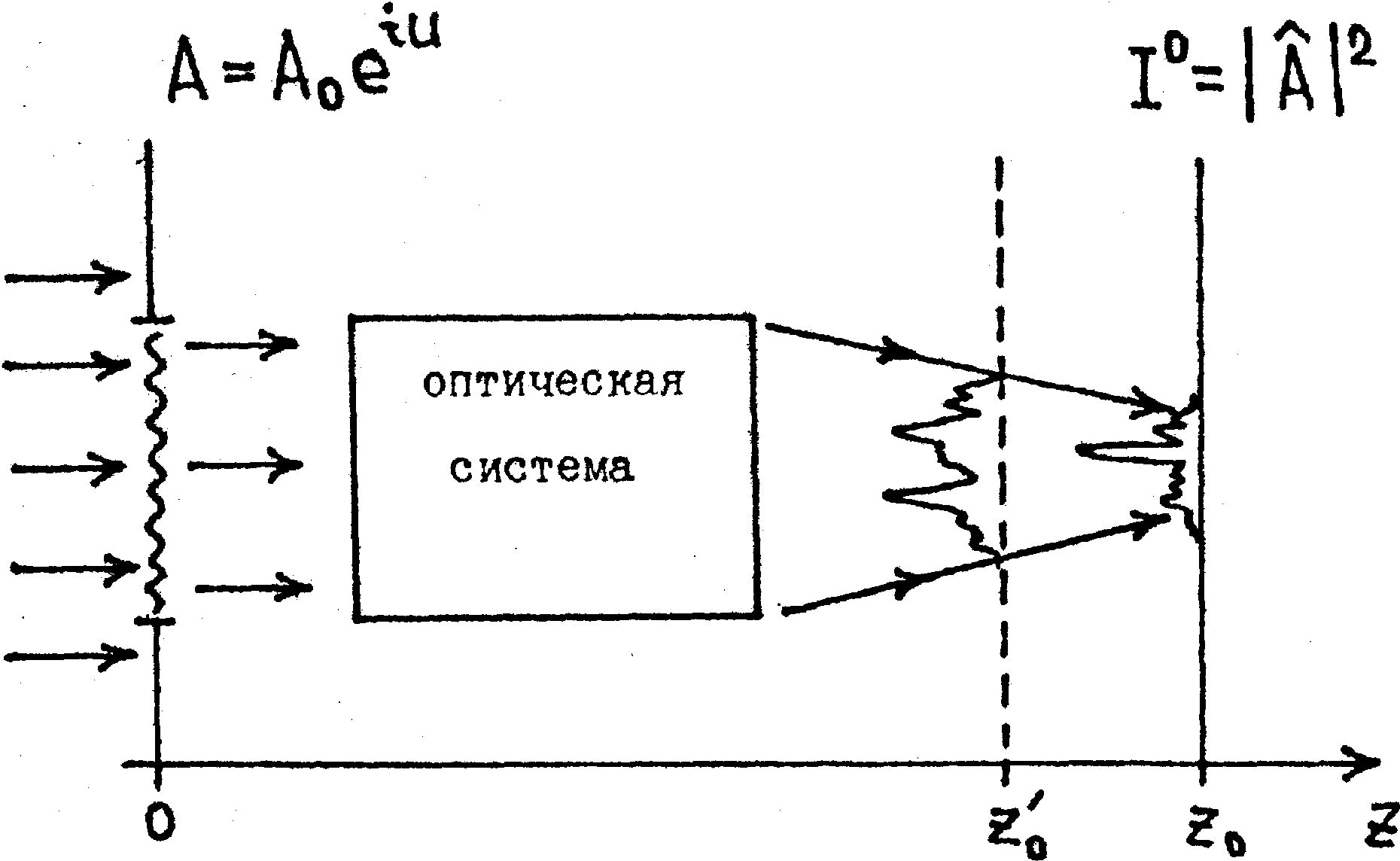
Рис.1. К постановке задачи восстановления фазы.
прогресс /4-5/. Весьма важный вопрос устойчивости обычно анализируется применительно к тому или иному алгоритму решения /I-3/.
К настоящему времени разработано довольно много алгоритмов решения фазовой проблемы /I-3, 6-9/. Наибольшее распространение в силу относительной простоты и удобства реализации на ЭВМ получили итерационные методы. Основой большинства таких методов является алгоритм Гершберга-Сакстона /7/. Он был предложен для восстановления фазы U поля по двум распределениям интенсивности А02 и I0=│Â│2 зарегистрированным, соответственно, на входе и в фокальной плоскости линзы. В дальнейшем были разработаны модификации этого алгоритма, позволяющие восстанавливать фазу поля по распределению интенсивности Ik0( ) в произвольной нефокальной плоскости Zk≠f, лежащей в зоне дифракции Френеля /8/. В работе /9/ на основе оригинального подхода было показано, что алгоритм Гершберга-Сакстона реализует градиентную процедуру минимизации некоторого функционала качества восстановления. Там же впервые было предложено использовать для восстановления ) в произвольной нефокальной плоскости Zk≠f, лежащей в зоне дифракции Френеля /8/. В работе /9/ на основе оригинального подхода было показано, что алгоритм Гершберга-Сакстона реализует градиентную процедуру минимизации некоторого функционала качества восстановления. Там же впервые было предложено использовать для восстановления
- l8 -
набор изображений, т.е. набор распределений интенсивностей, зафиксированных не в одной, а сразу в нескольких плоскостях регистрации Z=Zk, k=1,…,N. Оказалось, что построенный на этой основе алгоритм восстановления фазы по набору изображений имеет целый ряд преимуществ и, в частности, обладает высокой устойчивостью по отношению к аддитивному шуму в регистрируемой интенсивности Ik0 /9/. Вместе с тем, наличие аддитивного шума - не единственный источник ошибок в регистрируемой интенсивности. Они возникают и при неверном определении положений Zk этих плоскостей. Исследование влияния ошибок такого рода на устойчивость алгоритма восстановления по набору изображений до настоящего времени не проводилось. Попытка такого исследования численными методами и сделана в данной работе.
В расчетах использовалась квадратная сетка с числом узлов М=64 по каждой координате x, y. Начальная амплитуда падающей волны имела вид: A0( )=1 при │ )=1 при │ │=r≤b0 и A0( │=r≤b0 и A0( )=0 при r>b0 (принималось b0=1). Положение плоскостей регистрации Z=Zk удобно характеризовать безразмерными эквивалентными расстояниями: )=0 при r>b0 (принималось b0=1). Положение плоскостей регистрации Z=Zk удобно характеризовать безразмерными эквивалентными расстояниями:
Lk=Lg-1*Zkf/(f-Zk), (2)
где f - фокус линзы, Lg=0,5kb02 - значение дифракционной длины для заданной ширины входной апертуры b0, k=2Π/λ, λ - длина волны изучения. Заметим, L=∞ соответствует фокусу линзы. Эталонная, т.е. подлежащая восстановлению фаза задавалась в виде комбинации низших полиномов Цернике Sm( ), нормированных так, что ∫∫Sm( ), нормированных так, что ∫∫Sm( )Sn( )Sn( )d2r=Πδkm )d2r=Πδkm,
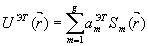 (3) (3)
В расчетах все amЭТ полагались одинаковыми и равными aЭТ. При выбранной нормировке среднеквадратичное отклонение δ ЭТ эталонной фазы от плоского волнового фронта равно 3а ЭТ. Начальное приближение U0( ) выбиралось таким же, как и в /9/, и соответствовало плоскому волновому фронту. ) выбиралось таким же, как и в /9/, и соответствовало плоскому волновому фронту.
- 19 -
Алгоритм восстановления фазы по набору изображений подробно описан в /9/. Фактически он представляет собой итерационную процедуру минимизации функционала суммарной ошибки восстановления Jm:
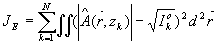
методом условного градиента. Для работы алгоритма необходимо вычисление поля изображения Â ( ,Zk) по "входному" полю A=A0eiUn в n-ой итерации. В данной работе Â определялось либо путем применения быстрого дискретного преобразования Фурье (БДПФ), если Zk=f, либо из численного решения параболического уравнения квазиоптики с применением БДПФ /IO/. ,Zk) по "входному" полю A=A0eiUn в n-ой итерации. В данной работе Â определялось либо путем применения быстрого дискретного преобразования Фурье (БДПФ), если Zk=f, либо из численного решения параболического уравнения квазиоптики с применением БДПФ /IO/.
Помимо значения критерия JE, качество восстановления фазы на n-ом шаге итерационного процесса оценивалось величиной
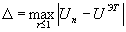 , ,
равной максимальному по апертуре отличию восстановленной и эталонной фаз,
Моделирование влияния ошибок в определении расстояний Lk до плоскостей регистрации осуществлялось следующим образом. Вычислялось распределение интенсивности Ĩk0(  ) поля с эталонной фазой в плоскостях L/k≠Lk интенсивность использовалась в качестве Iok( ) в функционале JE. ) в функционале JE.
На рис.2 приведены результаты восстановления фазы, имеющей умеренные абберации волнового фронта (aЭТ=0,1λ, δЭТ=0,3λ) θз различных наборов изображений, зарегистрированных в плоскостях, расстояние до которых определено с различной погрешностью. Нижняя (заштрихованная) половина рисунка отражает уменьшение значения критерия R=lg[J(n)E/J(0)E] через n интерационных шагов его минимизации (значение n также указано на рисунке). Верхняя часть рисунка показывает достигнутое значение ошибки Δ в длинах волн.
Когда восстановление фазы проводится по одному изображению, лежащему в зоне слабого проявления дифракционных эффектов ( L=0,1),
- 20 -
качественное восстановление остается возможным при погрешностях в определении расстояния до изображения до 2 % (L'=0.102). Дополнительная информация о распределении интенсивности поля в фокусе линзы позволяет ускорить сходимость процедуры восстановления (требуемое число итераций снижается с 50 до 30). В то же время допустимая ошибка в определении L остается примерно неизменной - до 5% (L' = О.105).
В случае регистрации интенсивности в трех плоскостях ( Lk=0.1, 0.5, ∞), положение одной из которых (в фокусе линзы L3=∞) считается известным точно, а положение двух других - с ошибкой, ситуация несколько ухудшается. Сильнее всего сказывается погрешность в определении расстояния до второй плоскости регистрации, лежащей в зоне более сильного проявления дифракционных эффектов (L2=0.55). Здесь изменение слагаемого критерия JE, соответствующего этому изображению: lg(J(n)2/J(0)2) в два раза меньше, чем в других плоскостях. Тем не менее, если погрешности имеют разный знак (L'1=О.102, L'2=0.49) и не превышают 2%, возможно восстановление фазы с максимальной ошибкой Δ=0,054λ ηа 31 итерацию. При 5-ти процентных ошибках качественное, восстановление волнового фронта становится невозможным.
Следует отметить, что при более сильных аберрациях эталонной фазы влияние ошибок измерений будет заметно возрастать. В качестве примера в правой части рис.2 показан результат попытки восстановления фазы при аЭТ =0.15λ (δЭТ=0.45λ) οо двум изображениям, расстояние до которых было определено с ошибкой в 5% (L1=0.1,L'1=0.105,L2=∞). Достигнутая за 40 итераций погрешность восстановления фазы составила Δ=0.15λ против Δ=0.092λ для менее сильных аберраций волнового фронта (aЭТ=O.Iλ).
Таким образом, погрешность в определении расстояний до плоскостей регистрации заметно снижает эффективность алгоритма восстановления фазы по набору изображений. Ошибку в 3-5% уже следует считать критической. Такая ситуация, однако, имеет место как при одной, так и при нескольких плоскостях регистрации. Поэтому
- 21 -
заметную неустойчивость восстановления фазы по отношению к ошибкам в расстоянии до плоскости регистрации следует считать общим недостатком как алгоритмов восстановления по набору изображений, так и классических алгоритмов типа алгоритма Гершберга-Сакстона. Учитывая отмеченные в /9/ преимущества алгоритмов восстановления по набору изображений, такие алгоритмы привлекательно использовать как основу при разработке экспресс-методов анализа волнового фронта, контроля качества оптических поверхностей. В этом случае удается преодолеть еще одну трудность, связанную с возможной неединственностью восстановления фазы из распределения интенсивности I0, зарегистрированного в фокусе линзы. Такая неединственность возникает, когда амплитуда входного поля A0=│A│ является четной функцией: А0(-  )=A 0(  ). В этом случае решением будет не только некоторая фаза U( ), но и функция U( ), но и функция U( )=-U( )=-U( ), в чем легко убедиться, непосредственно вычисляя интеграл Фурье. При этом получим, что ), в чем легко убедиться, непосредственно вычисляя интеграл Фурье. При этом получим, что
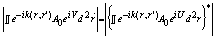 , ,
т.е. фазовые функции U и V приводят к одной и той же интенсивности выходного излучения I0=│Â│2. Ситуация резко меняется к лучшему в случае набора плоскостей регистрации, среди которых есть и нефокальные плоскости. В этом случае поля Â( ) и A( ) и A( ) связаны интегралом Френеля: ) связаны интегралом Френеля:
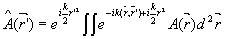 , ,
а фазовые функции U( ) и V( ) и V( )=-U(- )=-U(- ) формируют разное распределение интенсивности: ) формируют разное распределение интенсивности:
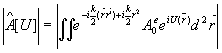 , ,
- 22 –
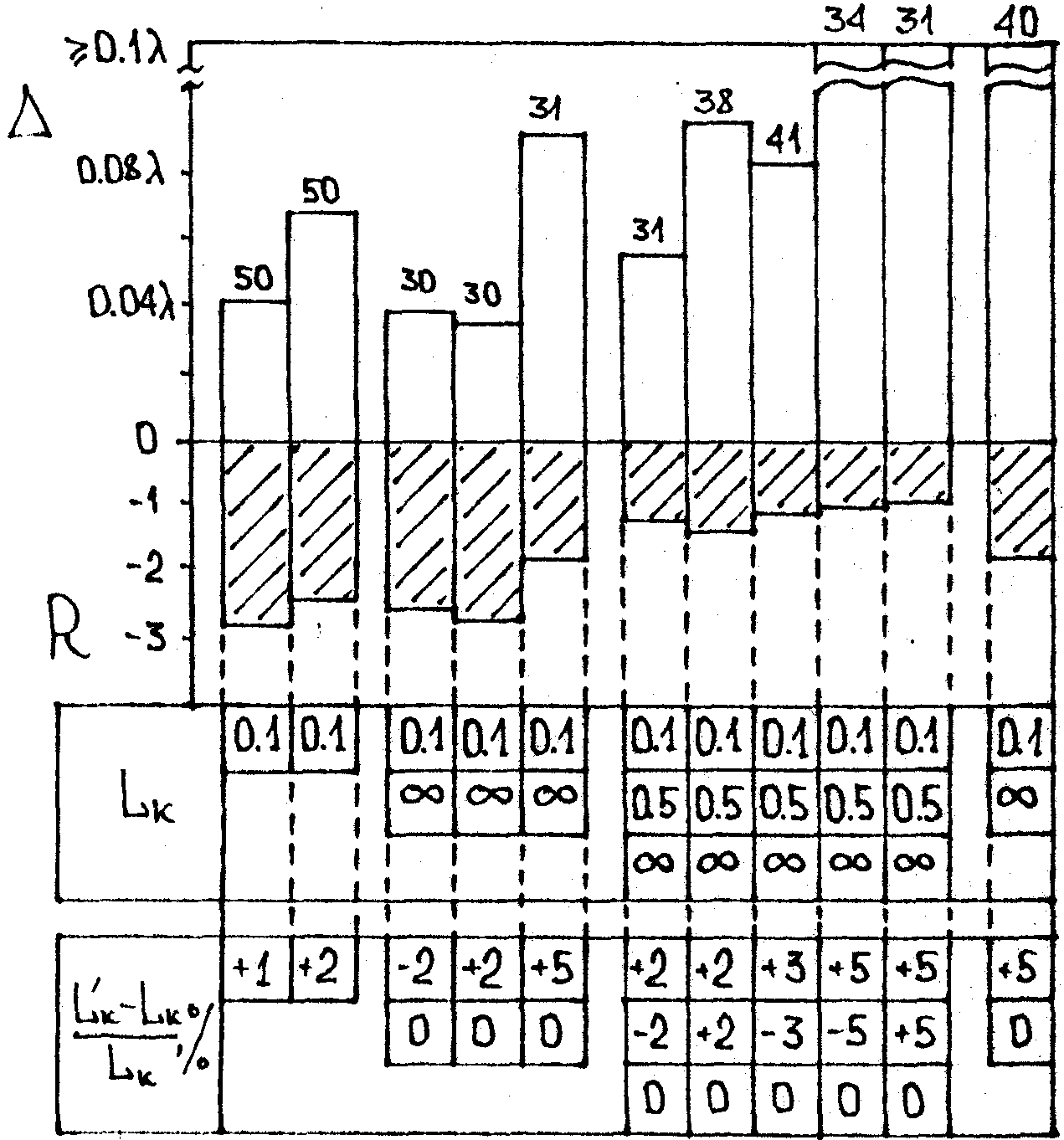
Рис.2, Эффективность восстановления фазы по набору изображений при наличии ошибки в определении расстояния до плоскости регистрации изображения:
LK - истинное расстояние, (Lk'-Lk)/Lk – относительная ошибка в определении Lk, R=lg[JE/J(0)E], 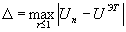 - достигнутая точность восстановления, - достигнутая точность восстановления,
- 23 –
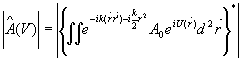
ясно видно, что │ [U]│≠│Â[V]│
Литература
Аблеков В.К., Колядин С.А., Фролов А.В. Высокоразрешающие оптические системы. М., Машиностроение, 1985, 176 с.
Обратные задачи в оптике (под ред.Болтса Г.П.), М., Машиностроение, 1984, 200 с.
Троицкий И.Н., Бакут П.А., Демин А.А., Сафронов А.Н. Современное состояние фазовой проблемы в оптике. Зарубежная радиоэлектроника, 1978, №11, с.3-40.
Клибанов М.В., Волостников В.Г., Котляр В.В. Доклады АН СССР, 1984, т.279, №6, 1348-1351.
Клибанов М.В., Доклады АН СССР, 1985, т.285, №2, с.278-280.
Fienup J.R., - Appl. Opt., 1982, v21, №15б 2758-2769
Serihberg R.W., Saxton W.O. – Optik, 1972, v35, №2, 237-26.
Rolleston R., George N. – Appl. Opt., 1986, v25, №2, 178-183.
Воронцов М.А., Сивоконь В.П. Труды XVII Всесоюзной школы по голографии и когерентной оптике, 1986, Л., ЛФТИ.
Сиклаш Е.А., Сигмен А.Е. ТИИЭР, 1974, т.62, №3, с.161-164.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

