|
|
 |
 |

|
| |
ОБРАБОТКА ИНТЕРФЕРЕНЦИОННЫХ ИЗОБРАЖЕНИЙ
С ПОМОЩЬЮ ГРАДИЕНТНОГО МЕТОДА
М.А.Воронцов, А.В.Кудряшов, В.И.Шмальгаузен
Предложен метод восстановления профиля оптических поверхностей по интерферограмме, основанный на итерационной процедуре оптимизации.
В настоящее время в оптике и акустике широкое применение получили интерферометрические измерения. Они позволяют регистрировать малые изменения параметров объекта (порядка длины волны источника когерентного излучения). Дешифрирование интерференционных картин производится ручным, полуавтоматическим и автоматическим способами /1-3/. Первых два вида обработки занимают много времени и весьма трудоемки. Автоматическое дешифрирование позволяет оперативно получать информацию об исследуемом объекте. Существующие методы автоматической обработки, как правило, предполагают последовательный ввод интерференционной картину в ЭВМ и последующее определение координат центров интерференционных полос. Таким образом, в интерферограмме используется лишь информация о координатах центров полос; вся остальная информация практически теряется. В настоящей работе предложен метод восстановления фазы из интерферограммы, основанный на анализе всего поля интерференционной картины.
Рассмотрим интерферограмму, полученную, например, с помощью стандартного интерферометра Майкельсона /4/. Интенсивность I(х,у) в каждой точке (х,у) интерференционной картины можно записать следующим образом:
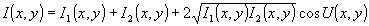 , (1) , (1)
где I 1(х,у), I2(x,у) - интенсивности опорного и предметного пучков, U(x,y) - искомая фазовая функция, например, профиль поверхности исследуемого зеркала. Суть предлагаемого метода заключается в следующем. Зная интенсивности опорной и объектной волны I1(x,у) и I2(x,y), синтезируем на ЭВМ интерферограмму по следующему алгоритму:
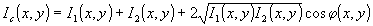 , (2) , (2)
где φ(х,у) - некоторая функция (оценка искомой фазы), которая на первом этапе задается произвольным образом. Степень близости истинной и синтезируемой интерферограмм будем оценивать функционалом
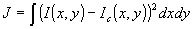 . (3) . (3)
Будем минимизировать функционал отличия J, варьируя фазу φ(x,у). Считаем, что при совпадении интерференционных картин, т.е. при J=0, фаза φ(x,у) совпадает с истинной. Алгоритм коррекции запишем в следующем виде:
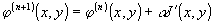 , (4) , (4)
где φ(x,у) фаза синтезируемой интерферограммы на n-ой итерации, J'(x,y) - градиент функционала J, α - величина шага градиентного метода.
Для получения градиента J'(x,у) дадим малое приращение Δφ(x,у) фазовой функции φ(x,у). Соответствующее изменение функционала обозначим через ΔJ: ΔJ=J(φ+Δφ)-J(φ). В соответствии с (1) и (2)
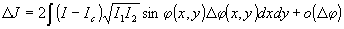 , (5) , (5)
где O(Δφ) - члены второго порядка малости относительно приращения Δφ(x,у). В соответствии с определением, градиент является
ИНТЕРФЕРОГРАММА
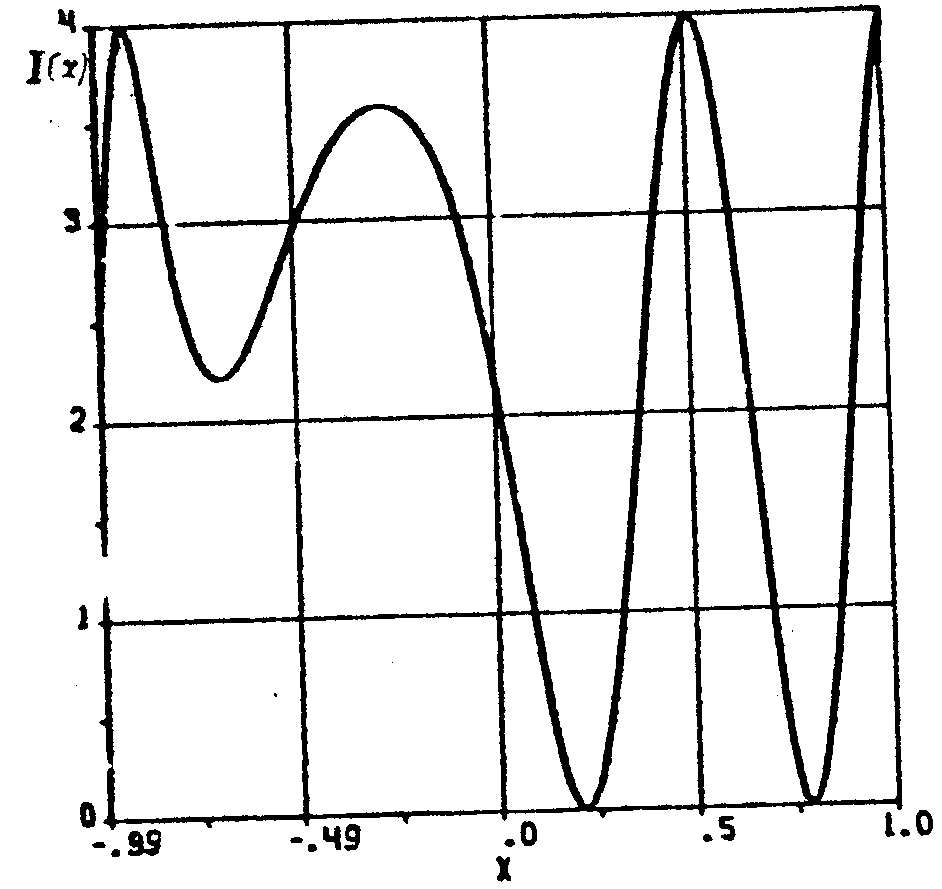
Рис.1. Распределение интенсивности I(х) в типичной интерференционной картине.
ФАЗА
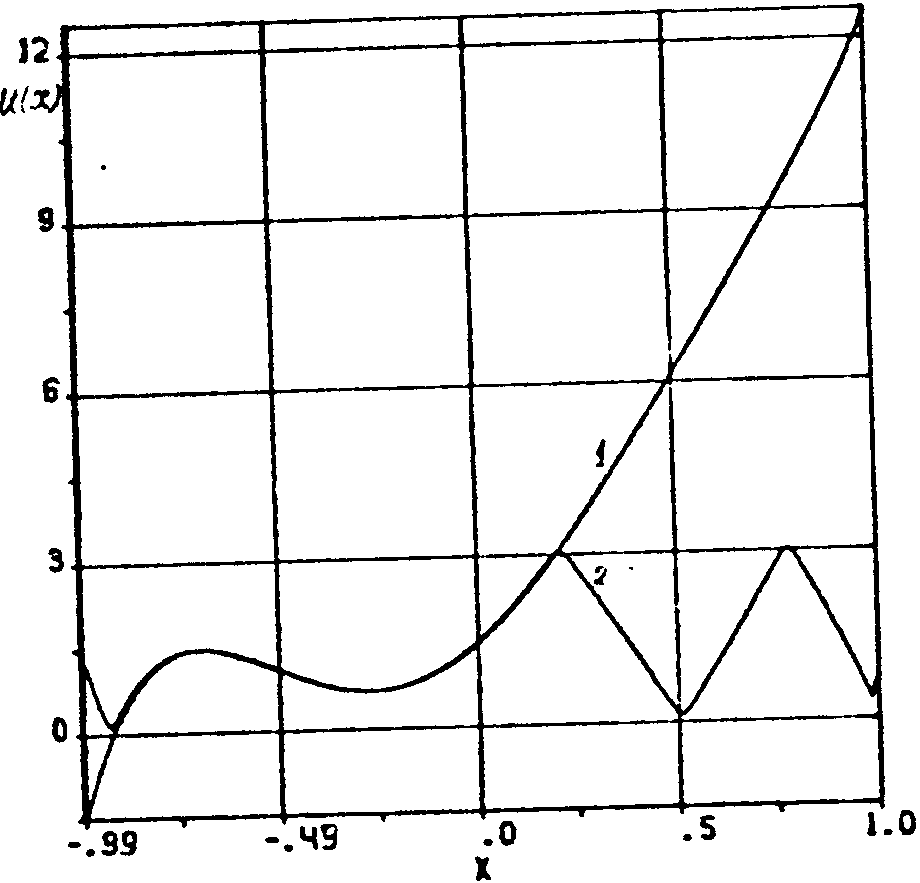
Рис.2. Набор фазовых функций U(х), соответствующих интерферограмме, изображенной на рис.1.
главной линейной частью этого приращения относительно Δ φ(υ,у), т.е.
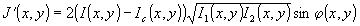 . (6) . (6)
Таким образом, алгоритм определения фаза сводится к следующей последовательности операций:
1. Раздельно регистрируются распределения интенсивностей: I, I 1, I 2.
2. Задается начальное приближение фазы φ(0)(x,y).
3. По формуле (2) синтезируется интерферограмма Ic(x,у).
4. Вычисляется функционал отличия (3).
5. По формуле (6) определяется градиент J'(x,y).
6. Вычисляется новое значение фазы φ(1)(x ,у) по алгоритму (4).
Далее последовательность операций 3-6 повторяется для фазовой функции φ(1)(х,у ) и т.д.
Вообще говоря, задача восстановления фазовой функции из интерферограммы не однозначна, т.е. одному и тому же распределению интенсивности в интерференционной картине (рис.1) соответствует множество решений U(х,y) (рис.2). В зависимости от выбора начального приближения φ (0)(х,у) в градиентном алгоритме (4) находится то или иное решение. Из всех решений, как правило, требуется найти наиболее плавно менявшуюся функцию U(х,у) (рис.2, кривая 1). Для этого предлагается в градиентном алгоритме (4) использовать метод последовательной интерполяции. Пусть для простоты, интенсивность I(х,у) зависит только от координаты х и задана в N точках (рассмотрим одно сечение интерферограммы). Для первых 3-х точек начальное приближение фазы выбирается произвольным, например, равным 1, т.е.
φ (0)(x 1)=φ(0)(x 2)=φ(0)(x 3)=1.
Далее, согласно градиентному алгоритму (4), в этих 3-х точках определяется значение фазы U(x1), U(x2), U(x3). Итерационный процесс (4) прерывается, когда отличие между текущим и
ИНТЕРФЕРОГРАММА
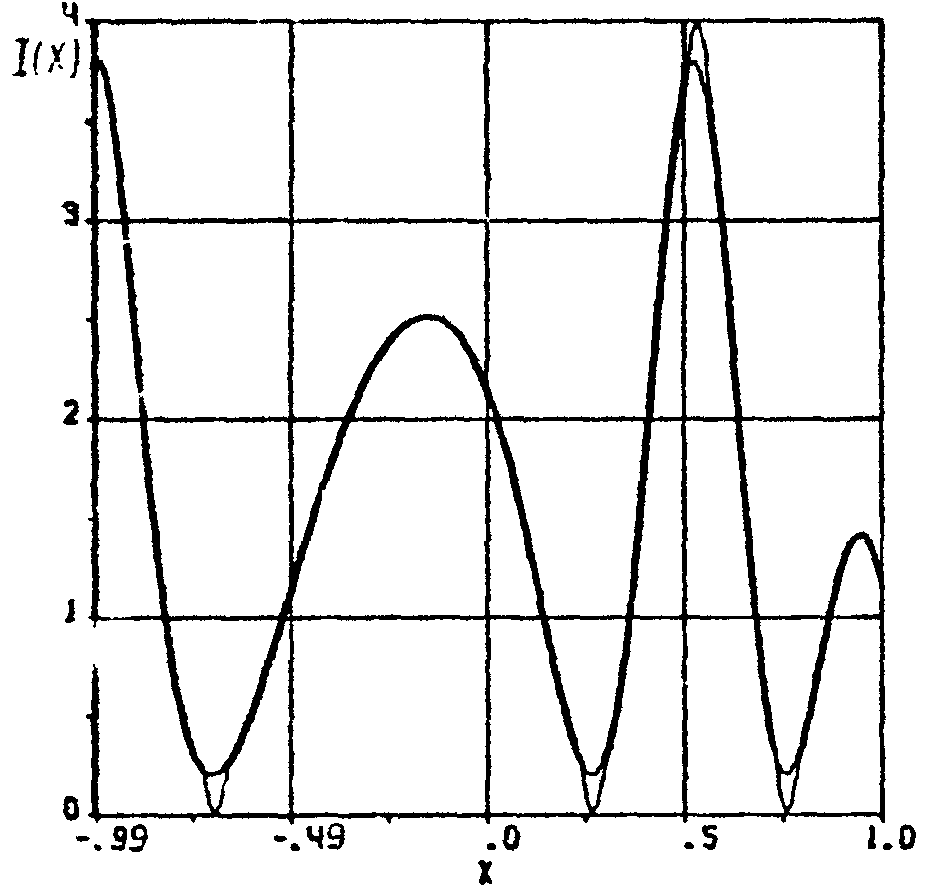
Рис.4. Распределение интенсивности в интерференционной картине, соответствующее фазовой функции U(x), изображенной на рис.3.
ФАЗА
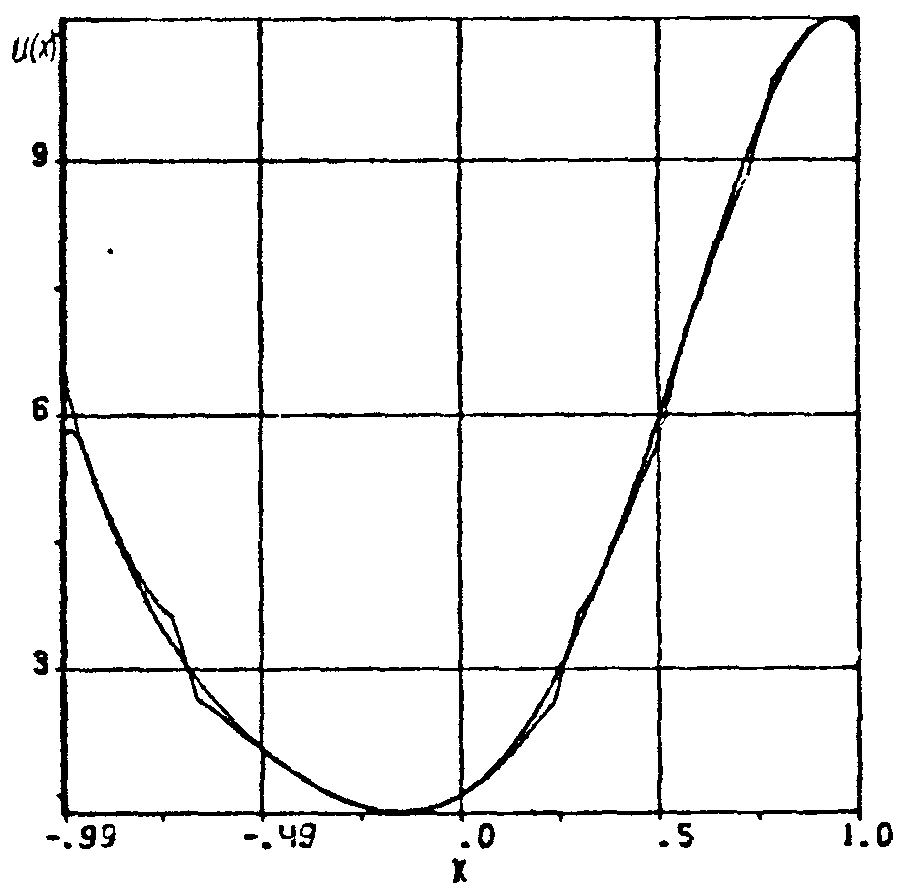
Рис.3. Фaзoвая функция и результат ее нахождения из интерферограммы.
предыдущим значениями фазы меньше заданного числа ε. Начальное приближение для следующей 4-ой точки φ(0)(х4) получим путем интерполяции полиномом второго порядка найденных значений U(х1), U(х2), U(х3) . Далее по градиентному алгоритму (4) вычисляется значением: U(х4). Для получения φ(0)(х5) интерполирующий полином сдвигается на одну точку, т.е. проводится через значения функций U(х2), U(х3), U(х4). Таким образом, находится начальное приближение в точно х5 и т.д.
Предположим, что контраст интерференционной картины γ(х, у) является медленно меняющейся функцией координат х,у и заранее неизвестен. Интерферограмму в этом случае можно описать следующим образом:
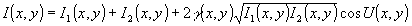 . .
В этом случае наибольшие трудности при восстановлении фазы по градиентному методу возникают в экстремумах интерферограммы (градиент J' в этих точках близок к 0). Поэтому в экстремальных точках предлагается вычислять фазу не градиентным методом, а интерполировать ее. Положим, I(х,у)=I(x). Далее, пусть в некоторой точке хi достигается максимум интерферограммы. Градиентным методом определяется фаза во всех точках вплоть до точки с координатой xi-2. Через U(хi-4), U(хi-3), U(хi-2) проводится кривая второго порядка и вычисляется начальное приближение в точке xi+2. В точках xi-1, xi, xi+1 фазовая функция не рассчитывается. Градиентным методом определяется значение U(хi+2) , далее точки U(хi-2) и U(хi+2) прямой. Такая процедура позволяет эффективно бороться с потерей контраста интерференционной картины. На рис.3 показан результат определения фазы
U(x)=1,5+3x+11x2+5x3–4x4–6x5
градиентным методом из интерферограммы (рис.4) при γ=0,9. Хорошо видно, что в местах перехода фазы через значения равные πn (n -целое число) восстановленная фаза имеет небольшую
неровность, которая легко сглаживается.
Таким образом, проведенные численные эксперименты показали эффективность использования метода для определения фазы, а также возможность борьбы с потерей контраста интерференционной картины. При этом для нахождения фазы используется вся информация, вводимая в ЭВМ. Надо отметить еще одно достоинство метода. Проведенные выше рассуждения для интерферограмм, полученных при помощи интерферометра с опорным пучком типа Майкельсона справедливы и для любого другого интерферометра, с той лишь разницей, что формулу (1), описывающую распределение интенсивности, нужно заменить на соответствующую данному прибору. При этом программы определения фазы практически останутся прежними.
Л и т е р а т у р а
1. Долгих С.Г., Устинов С.И. // Теоретическая и прикладная оптика, Материалы Всесоюзной конференции молодых ученых и специалистов. Л., 1984, с.214.
2. Косачев А.В. и др. // Теоретическая и прикладная оптика, Материалы Всесоюзной конференции молодых ученых и специалистов, Л., 1984, с.169.
3. Киричук B.C. и др. Автометрия, 1973, №1, с.63.
4. Д.Малакара. Оптический промышленный контроль. М., Машиностроение, 1985, с.200.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

