|
|
 |
 |

|
| |
ДИФРАКЦИОННАЯ ТОМОГРАФИЯ С ПРЕОБРАЗОВАНИЕ
ВОЛНОВОГО ФРОНТА
Г.Г.Левин, О.В.Старостенко
В настоящей работе кратко излагается суть и основные формулы дифракционной томографии (ДТ), возможность реализации известных алгоритмов ДТ (Фурье-синтеза и обратного распространения) применительно к оптическим измерениям. Предлагается схема оптического дифракционного процессора, достаточно просто реализующего предлагаемый алгоритм дифракционного суммарного изображения.
1. Основные уравнения дифракционной томографии
При исследовании внутренней структуры объектов при помощи того или иного вида излучения прежде всего подразумевается, что оно, проходя через объект, взаимодействует с ним. В этом случае рассматривают различные уравнения, описывающие распространение излучения внутри вещества. Наибольшее развитие получила томография, основанная на прямолинейной траектории распространения излучения внутри объекта (уравнение переноса, эйконала). Математическая запись такого распространения позволяет рассматривать прошедшее излучение как преобразование Радона изображения сечения объекта.
Очевидно, что данное условие выполняется только в некоторых частных случаях, которые определяются свойствами исследуемых объектов. Существует целый ряд томографических методов исследования внутренней структуры, базирующихся на других уравнениях распространения излучения в веществе /1/. В данной статье рассмотрим методы дифракционной томографии (ДТ), позволяющие учитывать сильные флуктуации показателя преломления в объекте
(см., например, /2,3/). Суть этих методов состоит в обращении задачи рассеяния, т.е. определение внутренней структуры объекта по рассеянному полю.
Теория обращения рассеяния была предложена Е.Вольфом /1/ и развита затем для решения задач акустической томографии и оптических измерений.
Ниже мы изложим некоторые моменты основополагающей работы Е.Вольфа /1/, при этом ограничимся двумерным случаем.
В томографии исследуется внутренняя структура объекта, заполненного неоднородной средой n(x,у). Если объект зондируется плоской волной Е0(х,у), то уравнение для поля Еl(x,у)=Е0(x,у)+Ер(x,у), где Ер - рассеянная часть поля, описывается уравнением Гельмгольца. Решение этого уравнения, т.е. выражение для рассеянной части поля в плоскости регистрации (голограммы) имеет вид:
, (1)
где ( x',l) - координаты точки наблюдения, 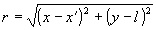 . Обозначим , . . Обозначим , .
В выражении ( 1) поле Еl представляет собой сумму падающей и рассеянной волн. Запишем уравнение падающей плоской волны в общем виде:
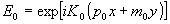 , ,
где р 0, m 0 - направляющие косинусы волны.
Используя условие борновского приближения, при котором E0>>Ep, следуя /1/, выражение (1) преобразуем к виду:
, (2)
где K=рK0, р≤1.
Выражение для А (K) представим в следующей форме /1/:
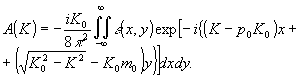 (3) (3)
Рассмотрим подробное выражение (3). Из него следует, что А( K) представляет собой фурье-образ искомой функции ε(х,у), но только той его части, которая задана на окружности радиуса K0 с центром в точке (-р0K 0, -m 0K 0). Для случая падения зондирующей плоской волны параллельно оси у центр окружности будет находится в точке (0,-K0).
Из вышеизложенного видно, что для восстановления двумерного распределения ε(x,у) недостаточно одной измеренной функции Е(x'), т.к. она определяет только одно сечение двумерного фурье-образа искомой величины. Для восстановления необходимо получить целый набор проекций под различными углами φ. Это соответствует томографической схеме зондирования объекта с различных направлений и накопления информации для последующей совместной обработки.
Формулы (2) и (3) составляют основу теории обращения рассеяния Е.Вольфа. На их базе разработаны алгоритмы дифракционной томографии. Наибольшее распространение получили два из них. Первый основан на связи Фурье-образов проекций и изображения сечения /1/. Второй - алгоритм обратного распространения - предложен Деване /4,5/.
2. Реализация алгоритмов дифракционной томографии
в оптической системе
Остановимся подробнее на обоих алгоритмах и рассмотрим возможность их реализации в оптической схеме.
Согласно первому алгоритму, уравнение томограммы f(х,y)=ε(х,у) можно записать в виде:
(4)
где U, V - координаты в частотной плоскости, - двумерное обратное преобразование Фурье, М - оператор аппроксимации,  - дифракционная проекция, - дифракционная проекция,
. (5)
Мы не будем останавливаться на особенностях реализации этого алгоритма на ЭВМ. Последовательность необходимых для этого операций в машине естественным образом вытекает из формулы (4), описывающей уравнение томограммы. Вычислительные особенности, которые приводят к существенным трудностям в конкретных расчетах, подробно анализируются в работах / 2,3/. Мы рассмотрим возможность восстановления томограммы оптическим способом, т.е. покажем, как реализовать этот алгоритм в оптическом процессоре. Это, тем более, необходимо, что практическое применение методов ДТ, особенно для случая оптического зондирования, сдерживается сложностями реализации измерений амплитуды и фазы рассеянного поля Ер(х'). Использование голографии на этапе регистрации, в принципе, позволяет восстановить комплексную амплитуду поля, но приводит к возникновению больших шумов на этапе ввода и восстановления голограмм на ЭВМ. Применение принципов оптической томографии, предложенной в работе /6/, которое предполагает выполнение преобразования волнового фронта, прошедшего через объект, впоследствии позволит существенно упростить обработку. В работах /7,8/ такой подход к построению томографического измерительного устройства для прямолинейного распространения излучения в объекте позволил избежать регистрации промежуточной информации и определить вид профиля показателя преломления в сечении объекта в реальном времени.
Для анализа возможности применения метода оптической томографии к объектам, в которых при распространении света присутствуют и дифракция, и рефракция, рассмотрим преобразования излучения, необходимые для восстановления томограмм. Согласно (4) и (5), в оптическом процессоре необходимо реализовать следующие операции.
1. Вычислить одномерное преобразование Фурье от каждой функции .
2. Запись голограммы поля 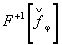 вдоль окружности радиуса K0 с координатами центра (K0Sinφ, K0Cosφ). вдоль окружности радиуса K0 с координатами центра (K0Sinφ, K0Cosφ).
3. Накопление голограмм спектров проекций для различных углов зондирования на одном регистраторе.
4.Аппроксимация спектров в частотной плоскости (оператор М).
Необходимость этой операции нужно пояснить. Нетрудно заметить, что в частотной плоскости, как и в случае томографии с прямолинейным распространением излучения имеет место существенная неравномерность отсчетов (низкие частоты заданы с большей плотностью отсчетов). Для компенсации этого в плоскости (U,V) необходима либо фильтрация низких частот, либо равномерная интерполяция /9/.
5. Умножение на функцию Ψ. Эта операция может быть совмещена с операциями 2-3, т.к. функция представляет собой фурье-образ поля точечного источника и может быть использована в качестве опорной волны.
6. Выполнение двумерного обратного преобразования Фурье. Если выполнение операций / 1/ и /3-6/ в оптическом процессоре достаточно очевидно, то для изгиба спектра проекции по окружности необходимо либо синтезировать специальные оптические элементы, либо использовать эффекты, связанные с дифракцией на решетке наклонно-падающего пучка. В любом случае выполнение операций /2/ оптически достаточно сложно, поэтому представляет интерес рассмотреть задание спектра на линии, занимающей промежуточное положение между окружностью радиуса K0 и прямой, касательной к ней в центре координат. Эта прямая соответствует расположению фурье-образа проекции при прямолинейной траектории
луча в объекте (теорема о центральном слое). Очевидно, что любые приближения сужают класс исследуемых объектов. Основной задачей в этом случае будет оценка точности реализации алгоритмов ДТ в зависимости от параметров объекта. В качестве таких обобщенных характеристик объекта целесообразно выбрать его размер z и максимальную пространственную частоту Kmax, понимая, что речь идет об интервале частот, в котором сосредоточена большая часть энергии сигнала. Необходимо помнить также, что эти параметры должны удовлетворять условию борновского приближения /10/.
Наиболее простым для оптической реализации алгоритма было бы задание спектра не на окружности, а на двух хордах, выходящих из начала координат частотной плоскости. Тогда достаточно внести в оптический тракт дополнительно призмы Дове, поворачивающие фурье-образы проекций. Оценим ширину спектра объекта в этом случае, полагая, что отклонение хорды от окружности не должно превышать Δ=1/z. Нетрудно заметить, что частота , при которой это условия выполняются, существенно превышает геометро-оптическое приближение.
На первый взгляд, оптическое восстановление томограмм проще выполнить, следуя алгоритму обратного распространения /4/. Рассмотрим подробнее этот алгоритм, согласно которому уравнение томограммы имеет вид:
(6)
Из (6) следуют операции, согласно которым надо преобразовать проекции 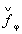 . .
1. Вычисление одномерного преобразования Фурье от проекции,
2. "Растяжение" фурье-образа проекции в направлении, перпендикулярном K - оператор R в (6).
3. Фильтрация "растянутой" проекции функцией
.
4. Вычисление обратного одномерного преобразования Фурье двумерной функции.
5. Поворот "растянутой" фильтрованной проекции на угол φ.
6. Последовательное голографического накопление суммы проекций, полученных под различными углами.
Восстановленное изображение с голограммы будет представлять собой томограмму.
Выполнение операций /1 ,2,4-6/ в оптической схеме не представляет сложности. Выполнение фильтрации (операции 3) представляет собой сложную задачу, т.к. фильтр описывается комплексной быстроосциллирущей функцией двух переменных (k,y).
Для того, чтобы облегчить оптическое восстановление томограммы, необходимо упростить алгоритм. Анализ фильтрующей функции показывает, что представление экспоненты в виде ряда не даст желаемого результата, т.к. множитель (y-l)>>λ. Наиболее целесообразно разложить в ряд корень в показателе экспоненты. В этом случав фильтрующая функция будет описываться выражением:
. (7)
Такое представление фильтра возможно для объектов, частота которых
.
Синтезировать фильтр, описывающийся выражением (7), проще, но самое главное, что эту функцию можно реализовать физически. В этом случае операцию фильтрации легко выполнить, записав голограмму Фурье-образа "растянутой" проекции с опорным пучком,
волновой фронт которого описывается таким же выражением - (7).
Проведенный анализ показывает, что оптическое восстановление томограмм по рассеянному полю, в принципе, возможно. К сожалению, рассмотренные алгоритмы восстановления и их оптическая реализация достаточно сложны, чтобы получить широкое распространение.
3. Алгоритм получения и фильтрации дифракционного
суммарного изображения
Анализ принципиальных схем оптических томографов показывает, что наиболее просто реализуется в оптике метод фильтрации суммарного изображения. При его выполнении процесс восстановления разбивается на два этапа: во-первых, синтез суммарного изображения, во-вторых, его фильтрация.
Методы получения суммарного изображения из проекций и уравнение, связывающее его с томограммой, разработаны для случая прямолинейной траектории луча в объекте. Покажем, что для дифракционной томографии также можно предложить аналогичный двуступенчатый алгоритм, и рассмотрим оптическую схему, его реализующую. Заметим, что прямой перенос алгоритма формирования суммарного изображения из радоновской в дифракционную томографию не позволяет получить простой связи между дифракционным суммарным изображением и искомой томограммой. Это приводит к необходимости введения дополнительных операций в алгоритм.
Рассмотрим подробнее необходимые преобразования волнового поля, для чего, используя уравнения (2) и (3), запишем выражение для дифракционной проекции в виде (с учетом введенных обозначений)
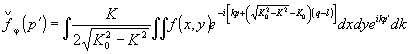 , (8) , (8)
где p=Sinφ+yCosφ, p'=x'Sinφ+y'Cosφ, q=-xCosφ+ySinφ.
Согласно алгоритму формирования суммарного изображения, "растянем" функцию в направлении q', перпендикулярном р. Заметим при этом, что в направлении q'V проекция не меняется.
Теперь, рассматривая проекцию как двумерную функцию, отфильтруем ее некоторой функцией g(p",q"). Причем фильтрацию будем осуществлять одномерную, вдоль оси р', рассматривая переменную q" как параметр. Тогда выражение (8) преобразуем к виду:
(9)
Согласно алгоритму формирования суммарного изображения, повернем каждую проекцию в плоскости (х", у") на угол φ и просуммируем их.
Тогда получившееся изображение fB(х",у") будет описываться выражением:
(10)
Применяя к внутреннему двукратному интегралу теорему о фурье-образе свертки, получим:
(11)
где ,
G - передаточная функция фильтра g.
Как уже отмечалось, достоинством суммарного изображения является простая связь его с искомым распределением в сечении объекта, определяемая уравнением свертки с известным ядром. Желая сохранить это свойство, выберем функцию G таким образом, чтобы
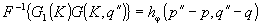 . (12) . (12)
Преобразуя (11), получим:
(13)
Если мы выберем функцию G вида:
, (14)
то функция hφ может быть представлена в виде:
.
Тогда выражение (10) можно преобразовать:
(15)
Для дальнейшего анализа рассмотрим параболическое приближение, т.е. положим, как и ранее,
. (16а)
Тогда, пренебрегая амплитудным множителем, представим (15) в
виде:
. (16)
Получим выражение для импульсного отклика дифракционного томографа в аналитическим виде. Заметим, что интеграл по K есть Фурье-преобразование функции Френеля, учитывая также, что
p"=x"sinφ+y"cosφ; q"=-xcosφ+y"cosφ,
нетрудно получить
(17)
здесь .
Сделаем в (17) замену переменных и преобразуем (17) к виду:
, (18)
здесь , - модифицированные функции Бесселя.
Анализ выражения (18) показывает, что импульсный отклик дифракционного томографа мало отличается от функции 1/4, соответствующей импульсному отклику в радоновской томографии.
Таким образом, для формирования дифракционного суммарного изображения, согласно предлагаемому алгоритму, необходимо выполнить следующие операции:
1. "растянуть" проекцию .
2. отфильтровать растянутую проекцию функцией G(K,q") (выражение (14));
3. повернуть полученную функцию на угол φ ;
4. просуммировать все проекции.
Нетрудно заметить, что выполнение операций 1,3,4 в оптическом дифракционном томографе совпадает с преобразованиями волнового фронта, необходимыми при формировании суммарного изображения в радоновской томографии. Очевидно, что и оптические схемы будут аналогичными. Существенным является выполнение операции 2. Анализируя функции фильтра G(K,q") в параболическом приближении, нетрудно заметить, что она совпадает с передаточной функцией конический линзы с переменным вдоль оси q фокусным расстоянием f=l-q, т.е. переотображением растянутой проекции тонкой конической линзы, ось которой параллельна оси q, будет эквивалентно фильтрации проекции функции:
. (19)
Таким образом, предложенный алгоритм суммарного дифракционного изображения и оптическая схема, его реализующая, позволяют достаточно просто визуализировать в некотором приближении (16а) изображение сечения объекта. Последующая обработка суммарного дифракционного изображения, сводящаяся к решению уравнения (16), позволяет восстановить томограмму.
Л и т е р а т у р а
1. Wolf E. Opt.Commun., 1969, v.1, 7, pp.153-156.
2. Kak А.С., Pan S.X. IEEE Trans. on ASSP, 1983, T.ASSP-31, 5, pp.1262-1275.
3. Sleney M., Kak A.C. Proc.SPIE, v. 413, 1983, pp.2-10.
4. Devaney A.I. IEEE Trans. on SU, 1903, v.SU-30, 6, pp.355-364.
5. Devaney A.I. Proc.SPIE, 1982 , у.358, pp.10-16.
6. Вишняков Г.Н., Левин Г.Г. Оптика и спектроскопия, 1982, т.53, №4, с.731-735.
7. Вишняков Г.Н., Левин Г.Г. Оптика и спектроскопия, 1985, т.58, №3, с.629-633.
8. Вишняков Г.Н., Левин Г.Г. Оптика и спектроскопия, 1982, т.53, №5, с.929-932.
9. Вишняков Г.Н., Левин Г.Г. Оптика и спектроскопия, 1984, т.56, №5, c.933-935.
10. Carter W.H. Proc.SPIE., 1983, v.413, pp.65-73.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

