|
|
 |
 |

|
| |
ИССЛЕДОВАНИЕ РАССЕИВАЮЩИХ СРЕД И ВИЗУАЛИЗАЦИЯ ФАЗОВЫХ ОБЪЕКТОВ В ЧАСТИЧНО КОГЕРЕНТНОМ ИЗЛУЧЕНИИ
Н.Г.Власов. Э.Г.Семенов, М.Э.Соколова
Информация, содержавшаяся в модуле |γ(τ)| функции взаимной когерентности, традиционно использовалась для исследования источников излучения и корреляционных свойств волновых полей /1/. С развитием голографии эта традиция начала нарушаться. В кратком сообщении /2/ было оточено, что длина когерентности lк излучения, применяемого при записи голограммы, определяет глубину резко изображаемого пространства на восстановленном изображении, а его расстояние до голограммы зависит от разности оптического пути между объектными и опорными волновыми полями, что позволяет в значительной мере устранить размытие изображения, вызванное расположением стационарных рассеивателей (микрочастиц) между голограммой и записываемым на нее объектом.
1. Исследование частично рассеивающих сред
Была опубликована группа работ, в которой излучение с ограниченной длиной когерентности использовалось для диагностики частично рассеивающих сред. Так, в /3/ излучение с ограниченной длиной когерентности направлялось в интерферометр Майкельсона, в одном из плеч которого находилась среда с рассеивавшими частицами. Намерение задержки опорного волнового поля относительно объектного, регулируемое смещением зеркала в опорном плече интерферометра, позволяло получать интерференционную картину, образованную освещающим излучением, рассеянным в обратном направлении с раз-
личных глубин. По полученной интерференционной картине определялись статистические и оптические свойства среды. В /3/ отмечалось также, что по своим диагносцирующим свойствам частично когерентное излучение эквивалентно излучению импульсного лазера с длительностью импульса Δt=lк/с, гдe c - скорость. Так, при lк=100 мкм эквивалентная длительность импульса Δt=3∙10-13 с, что позволяет получать информацию, усредненную по очень малой толщине исследуемой среды.
В /4/ описанный в /3/ метод был обобщен на случай среды с подвижными рассеивателями, то есть фактически были рассмотрены допплеровские измерения в частично когерентном излучении. Было получено соотношение, аналогичное по структуре уравнению лазерной локации, позволяющее восстановить профиль показателя ослабления и обратного рассеяния, а при наличии некоторой априорной информации о среде - и некоторые ее микрофизические характеристики.
Существенное методическое значение имела работа /5/, в которой за счет наклонного освещения плоской диффузно рассеивающей поверхности за одну экспозицию записывался непрерывный набор изменений разности длины оптического пути между объектным и опорным волновыми полями. Яркость восстановленного изображения измерялась от максимального до нулевого в соответствии с изменением разности оптических путей от нулевого до Δlmax=lк и описывалась квадратом модуля функции временной когерентности освещающего излучения. Таким образом, было наглядно продемонстрировано, что отлично от классической интерферометрии, где |γ(τ)| определяется дискретно с усреднением по периоду интерференционных полос, голография позволяет получать и измерять непрерывное значение |γ(τ)|2.
Указанное обстоятельство позволило авторам работы /6/ применить голографическую запись в частично когерентном излучении для получения восстановленного изображения слоя рассеивающей жидкости на заданной глубине, регулируя ее задержкой между опорным и объектным волновыми полями. В /6/ использовался лазер с длиной
когерентности lк=6 см, в связи с чем изменение разности оптических путей по голограмме
δ(ΔL)<<l к (1)
не рассматривалось. Авторы данной работы пришли к выводу, что применение голографического метода позволило уверенно идентифицировать объект при коэффициенте пропускания Т рассеивающей среды Т=1,5∙10 -8, в то время как обычная фотография при Т=10-6 даже не позволят обнаружить присутствие объекта.
Аналогия между диагностирующими свойствами частично когерентного излучения непрерывного источника и излучением импульсного источника, предложенная в /3/, была обобщена и развита в нескольких работах Н.Абрамсона, из которых наиболее полной публикацией является /7/. В /7/ экспериментально продемонстрировано, что при определенном выборе геометрии эксперимента можно получать световые сечения трехмерных диффузно отражающих объектов. Если же диффузно рассеивающая поверхность плоская, то на ее восстановленном изображении можно получать сечения волнового фронта. соответствующие различным моментам времени, то есть регистрировать свет в процессе распространения. В целом, как показал Н.Абрамсон, голография в частично когерентном излучении позволяет получать временную развертку исследуемого процесса. В частности, применение пикосекундных лазеров позволяет визуализировать динамику протекания процесса с рекордным разрешением. Вероятно, данная работа окажет влияние и на дальнейшее развитие голографии быстропротекающих процессов.
Отметим, что световые сечения трехмерных диффузно отражающих объектов можно получать и при помощи спекл-фотографии в частично когерентном излучении /8/. Существенным преимуществом спекл-фотографии является значительное упрощение схемы эксперимента и получение изображения именно заданного сечения, что сводится просто к фокусировке фотоаппарата на нужную плоскость. Недостаток заключается в увеличении длительности экспозиции, так как в спекл-фотографии, в отличие от голографии, отсутствует ин-
тенсивный опорный пучок. Однако последний недостаток можно частично устранить, применяя мощные лазеры, работающие в многомодовом режиме. В последовавшей за /8/ работой /9/ было показано, что при помощи спекл-фотографии в частично-когерентном излучении можно получать, как и в голографии, изображение объекта, отделенного от фотографирующего объектива рассеивающей или турбулентной средой.
В /10/ предложена оптическая схема записи голограммы в частично когерентном излучении, позволяющая получать томографические сечения рассеивающей среды, состоящей из микрочастиц. При помощи цилиндрического коллиматора в исследуемом объеме 1 высвечивается слой толщиной ~1 мм в направлении, перпендикулярном оптической оси объектива, фокусирующего одну из освещенных плоскостей объекта в плоскость фотопластинки. Схема записи голограммы построена так, что из всего освещенного объема на нее записывается только тонкий слей толщиной ~lк.
В /11/ было предложено голографическое трехмерное зрение роботов, позволяющее последним ориентироваться в пространстве, содержащем диффузно отражающие объекты. В предложенном методе интенсивность I(х,у) восстановленного изображения пропорциональна произведению квадратов модулей функций комплексного отражения объекта U(x,y) и функции временной когерентности γ(2R(x,y)/c):
I(x,y)~|U(x,y)|2 |γ[2R(x,y)/c]|2, (2)
где R(x,y) - расстояние до предметов, записанных на голограмму. Однако, несмотря на оригинальность и привлекательность такого предложения, его практическая осуществимость представляется проблематичной в связи с необходимостью учета изменения отражающих свойств, описываемых множителем |U(x,у)|2, от предмета к предмету по поверхности каждого предмета.
Таким образом, можно констатировать, что в последние годы начало развиваться новое направление в оптико-физических измерениях, основанное на использовании информации, заключенной в мо-
дуле функции взаимной когерентности. В настоящее время область применения этого направления ограничивается наблюдением объекта через рассеивающую среду, получением изображений тонких слоев и сечений рассеивающих сред и исследованием их свойств, а также получением световых сечений трехмерных диффузно отражающих объектов. Принципиально новое применение рассматривается в следующем разделе.
2. Визуализация прозрачных объектов
Под прозрачным объектом понимают, как известно, объект, функция комплексного пропускания которого имеет вид еiφ(x,у). При освещении такого объекта плоской волной с постоянной амплитудой а(х,у)=const=а, волновое поле U(х,у) непосредственно за объектом имеет вид U(х,y)=aeiφ(x,y).
Данное определение прозрачного объекта возможно именно введу своей краткости, не позволяет дать общее, систематизированное описание методов визуализации прозрачных объектов, находящих традиционно широкое применение в аэро- и гидродинамике, диагностике плазмы, исследовании пламени, контроля качества оптических элементов и т.д. В настоящей работе делается попытка дать единый подход к описанию и систематизации таких методов.
Представим волновое поде U(х,у) в виде суммы плоских волн, перейдя для упрощения математической записи к одномерному случаю:
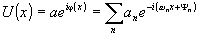 . (3) . (3)
Введем теперь определение прозрачного объекта как такого объекта, за которым сумма плоских воли непосредственно сфазирована таким образом, что амплитуда а(х) результирующего волнового поля Uх является постоянной, не зависящей от пространственной координаты х: а(х)= const=а.
В частности, при освещении прозрачного объекта плоской волной единичной амплитуды сумма плоских волн на выходе сфазирована
так, что a=1. Отметим теперь, что спектр пространственных частот прозрачных объектов в большинстве случаев, представляющих практический интерес, достаточно узок и передается оптической системой, если не приняты специальные меры, почти без изменений. Поэтому волновое поле в плоскости изображения, как и в оптически сопряженной плоскости предметов, описывается уравнением (3), и изображение объекта, в соответствии с высказанным определением, также остается прозрачным. Действительно, наблюдаемая или регистрируемая каким-либо квадратичным детектором интенсивность I(х)=|U(х)|2=a 2 является постоянной, в плоскости изображения не зависящей от пространственных координат.
Определим теперь операцию визуализации изображения прозрачного объекта как дефазировку суммы плоских волн (3), приводящую к тому, что интенсивность объектного волнового поля становится функцией пространственных координат, для которой 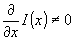 . .
Покажем, что такое определение позволяет с единой точки зрения описать все методы визуализации прозрачных объектов. Действительно, в интерферометрах обычного типа дефазировка достигается за счет того, что к спектру пространственных частот объектного волнового поля добавляются пространственные частоты другого, опорного волнового поля, сформированного в виде плоской или сферической волны. В сдвиговых интерферометрах или в методах дефокусировки дефазировка достигается добавлением к объектному волновому полю в каждой данной точке плоскости изображения пространственных частот объектных волновых полей, соответствующих другим, соседним точкам плоскости изображения. В голографических интерферометрах или интерферометрах с оптической линией задержки /12/ дефазирующим также является волновое поле, образованное из объектного и смещенное, в отличие от предыдущего случая, не по пространственным, а по временным координатам. Наконец, в теневых методах или методах типа предложенного Цернике или основанного на преобразовании Гильберта /13/ дефазировка достигается преобразованием спектра пространственных частот самого объектного волнового поля.
Обобщая приведенные примеры, операцию визуализации целесооб-
разно представить как интерференцию объектного и дефазирующего волновых полей, имея в виду следующие аргументы: процесс образования изображения носит интерференционный характер; как минимум половина методов визуализации прозрачных объектов основана на интерферометрии. Кроме того, в интерферометрии четко определено понятие видности (или контраста) интерференционных полос / 1/, которое можно попытаться обобщить /14/ на базе описания контраста изображения фазового объекта, визуализированного теневыми методами. Для этого случая в работе /14/ для описания распределения интенсивности в плоскости изображения использовано следующее выражение:
I(x)=|e iφ(x)-α∙S(x)| 2, (4)
где S(x) - часть объектного волнового поля, задержанного или видоизмененного в плоскости пространственных частот, а α - некоторый коэффициент, вообще говоря, комплексный, позволяющий описать измерение фазы части объектного волнового поля в методе Цернике, при преобразовании Гильберта и т.д. Обозначив дефазирующее волновое поле V(x)=-αS(x), для описания общего случая, включающего, в частности, интерферометры пространственного и временного сдвига, сумму объектного и дефазирующего волновых полей представим в виде:
U(x)=U oδ(x1,t)+Ug(x2,t+τ). (5)
Строгое рассмотрение интерференции волновых полей, смещенных по пространственным и временным координатам, дается, как известно, в теории когерентности / 1/, описывающей корреляционные свойства волновых полей при их трансляции в пространственно-временных координатах. Согласно /1/,
I(x)=<|U oδ(x1,t)+Ug(x2,t+τ)|>, (6)
где угловые скобки означают усреднение по времени. После усреднения (6) принимает традиционный вид:
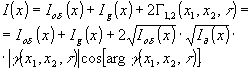 (7) (7)
Так как для прозрачного объекта I (x)=const, а операция визуализации переводит информацию о распределении фазы по объекту в распределение интенсивности, запишем условие визуализации, как это было сделано выше, в виде 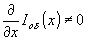 . Имея в виду, что . Имея в виду, что 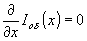 по определению фазового объекта, и учитывая, что информация о Ig(x) содержится в Г1,2 по определению фазового объекта, и учитывая, что информация о Ig(x) содержится в Г1,2(x 1,x 2,τ), условие визуализации перезапишем в виде:
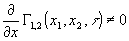 (8) (8)
или
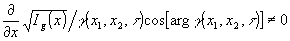 . (9) . (9)
Очевидно, что условие (9) выполняется, если производная хотя бы от одного сомножителя не равна нулю.
Уравнения (8) и (9) в наиболее общем виде записывают условие визуализации прозрачных объектов. Действительно, неравенство нули последнего сомножителя соответствует интерференционным методам, а первого сомножителя - методам, основанным на преобразовании части объектного волнового поля в плоскости пространственных частот. Из (9) следует, что есть новый путь визуализации прозрачных фазовых объектов, основанный на использовании информации, заключенной в модуле функции взаимной когерентности и устранении вли-
яния аргумента этой функции. Решение поставленной задачи достигается при помощи записи голограммы прозрачного объекта в частично когерентном излучении. Как известно, голограмму прозрачного объекта можно рассматривать как интерферограмму, полученную при настройке интерферометра на режим частых полос конечной ширины, и описывать уравнением (7). При записи голограммы в частично когерентном излучении ее амплитудное пропускание Т 1(х) в первом порядке дифракции, распространяющимся в том же направлении, что и объектное волновое поле, описывается одним из перекрестных членов уравнения (6):
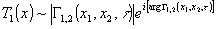 . (10) . (10)
В отличие от известных интерференционно-голографических методов визуализации прозрачных объектов в когерентном излучении перейдем сразу к наблюдению восстановленного изображения, то есть к регистрации интенсивности I1(x) восстановленного волнового поля, что математически описывается как воздействие на него квадратичного детектора:
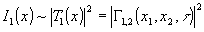 . .
Таким образом, сохранилась только та информация, которая была заключена в модуле функции взаимной когерентности, а мешавшая в данном случае информация, заключенная в аргументе функции 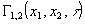 , устранена. , устранена.
Рассмотрим следующий пример метода визуализации, входящего в группу, для которой 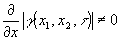 , согласно работе /15/. Пусть голограмма записывается в излучении, частично когерентном по временной координате, т.е. х1=х2 , согласно работе /15/. Пусть голограмма записывается в излучении, частично когерентном по временной координате, т.е. х1=х2, γ=γ(τ) (πис.1). Дифракционная решетка, освещенная частично когерентным излучением, фокусируется оптической системой, пропускающей только ±1 порядки дифракции, на фотопластинку-голограмму. Схема подобного типа была предложена Е.Лейтом для записи на голограмму транспарантов (фотографий) в нелазерном излучении /13/.
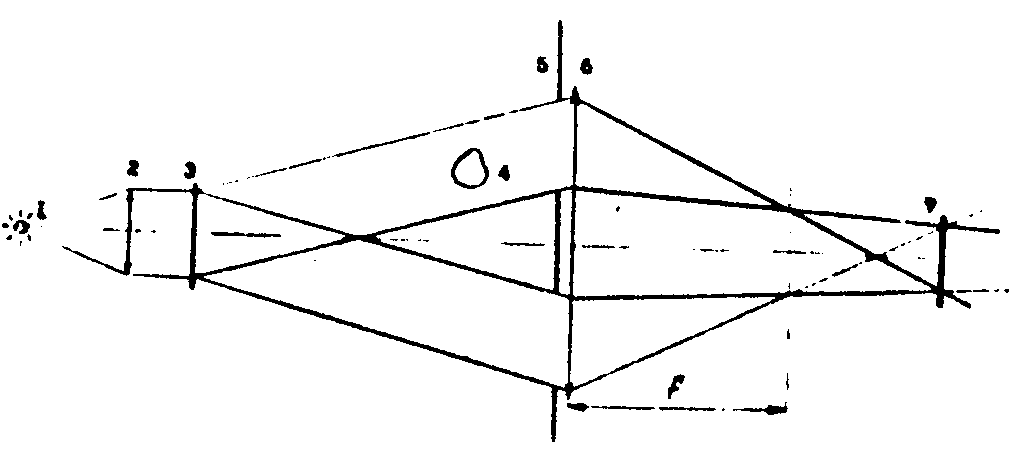
Рис.1. Оптическая схема получения голограмм.
1-диафрагмированное изображение освещающего источника, созданное конденсорной линзой; 2-линза коллиматора; 3-дифракционная решетка; 4-прозрачный объект; 5-диафрагма с двумя отверстиями; 6-линза; 7-фотопластинка-голограмма.
В данном случав излучение, распространяющееся в одном порядке дифракции, проходит визуализируемый объект, а распространяющееся в сопряженном порядке используется как опорное. При записи голограммы прозрачного объекта для тех его участков, для которых ΔL=ΔLmax=l к, видность интерференционных полос, составляющих микроструктуру голограммы, равна нулю и голограмма не записывается. Следовательно, при восстановлении изображения эти участки наблюдаются как темные. Участки вблизи объекта, для которых ΔL=0, записываются с единичной видностью, восстанавливаются как яркие. Для промежуточного случая, когда 0≤ΔL≤lк, амплитудное пропускание голограммы пропорционально |γ(τ)| и восстанавливается, соответственно, полутоновое изображение, распределение интенсивности по которому пропорционально |γ(τ)|2. Отметим, что нелинейность регистрирующей среда не искажает в данном случае восстановленного изоб-
ражения и приводит лишь к появлению высших порядков дифракции при освещении голограммы.
Как и в классической интерферометрии, получение количественных данных заключается в расчете распределения показателя преломления либо его изменения в выбранном сечении объекта, для чего в начале строится график изменения Δ L по прямой, на которую проектируется при просвечивании освещающим излучением выбранное для расчета сечение объекта. В классической и голографической интерферометрии эта операция во многих случаях может быть выполнена только квалифицированным оператором. В данном случае она сводится просто к фотометрированию распределения интенсивности вдоль названной прямой, что позволяет полностью автоматизировать ввод экспериментальных данных в ЭВМ и получение количественных данных.
Предложенный метод проверялся моделированием на ЭВЫ и непосредственным экспериментом. Для машинного эксперимента был выбран часто встречающиеся в практике осесимметричный объект с комплексной функцией пропускания гауссовского типа. Направление освещения совпадало с осью х. При этих условиях в выбранном для получения количественных данных сечении изменение оптического пути по объекту ΔL(у) также является функцией гауссовского типа (рис.2а). Моделировалось освещающее излучение, в котором спектральная плотность мощности в интервале длин волн λ 0+Δλ была постоянной, а вне его равнялась нулю - случай, характерный для изучения теплового источника, прошедшего через светофильтр. Для излучения такого типа функция γ(τ)=γ(ΔL) имеет, как известно /13/, вид Sin z/z, характеризующийся достаточно протяженным участком (рис.2б), близким к линейному. Влияние нелинейного участка может быть устранено введением небольшой дополнительной задержки в одно из плеч оптической схемы, показанной на рис.1. Если же сделать задержку равной ΔLmax, то восстановленное изображение является негативным по отношению к первоначальному.
В эксперименте в качестве источника излучения использовалась ртутная лампа со светофильтром, выделявшим зеленую линию. Было получено визуализированное изображение прозрачного фазового объ-
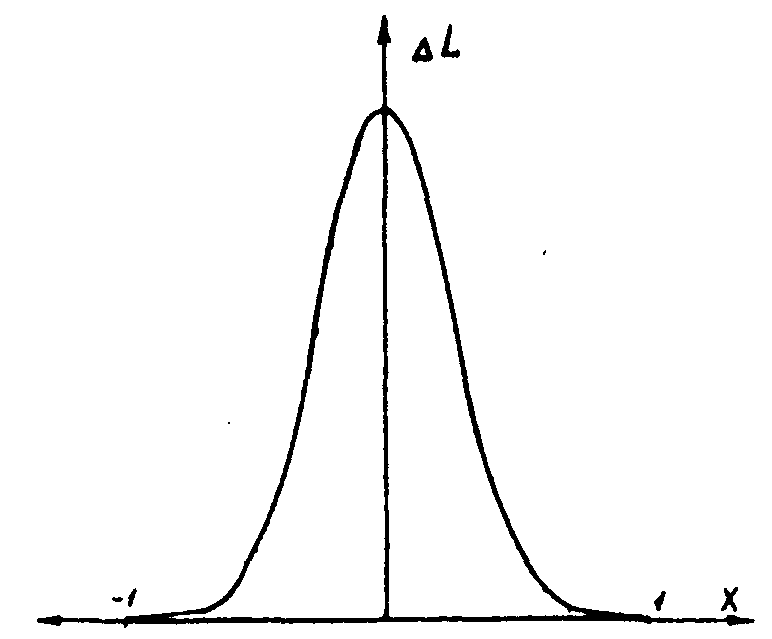
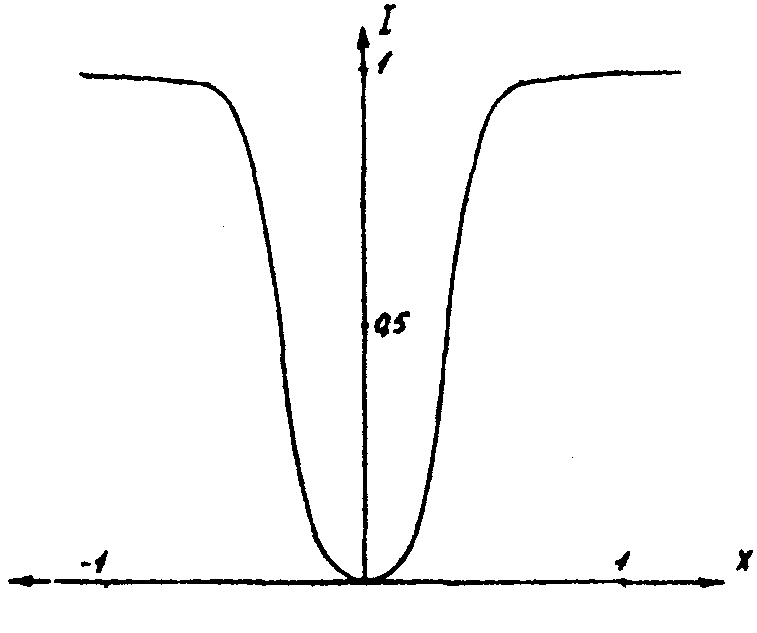
Рис.2. Изменение оптического пути по объекту в одном из его сечений (а) и соответствующее распределение интенсивности на восстановленном изображении (б).
екта - высохшей капли бесцветного лака, нанесенной на плоскопараллельную стеклянную пластинку. Качество восстановленного изображения было выше получаемого обычно при помощи лазера, так как в связи с ограниченной когерентностью излучения ртутной лампы устранялись шумы (дифракция на пылинках и других дефектах оптических элементов), характерные для полностью когерентного излучения.
В заключение оценим область применения предложенного способа. Требуемую длину когерентности можно установить, регулируя диапазон длин волн освещающего излучения за счет выбора полосы пропускания светофильтра, области сенсибилизации регистрирующей среды либо типом источника излучения. Так, для белого света и спектроскопических фотоэмульсий lк=1,5 мкм, для голографической фотоэмульсии типа "Микрат-ВР", сенсибилизированной на максимум чувствительности при λ=0,63 мкм, lк=3,6 мкм, для пикосекундных лазеров и ртутных ламп со светофильтром lк равна нескольким десяткам мкм, для голографических лазеров - несколько десятков сантиметров и более. Таким образом, по сравнению с интерферометрией предложенный метод обладает большим диапазоном измерений, несколько уступая ей, однако, по чувствительности.
Л и т е р а т у р а
1. Борн М., Вольф Э. Основы оптики, М., Наука. 355с., 1970.
2. Caulfield H.J. J.Opt.,Soc.Am., 1968, 58, 2, 276-277.
3. Иванов И.П.. Чайковский А.П., Кумейша А.А. ЖПС, 1978, 28, №3, с.518-525.
4. Иванов А.П., Чайковский А.П., Кумейша А.А. ДАН БССР, 1979, т.23, №6, с.503-506.
5. Стаселько Д.И., Денисюк Ю.H., Смирнов А.Г. "Оптика и спектроскопия", 1969, т.26, №3, с.413-420.
6. Гурский И.М., Иванов А.П. ДАН БССР, 1981, 25, №1, с.16-1 9.
7. Абрамсон Н., Appl.Opt., 1983, 22, №2, с.215-232.
8. Власов Н.Г., Мацонашвили Р.Б., Пресняков Ю.П., Степанов Б.М. Материалы XI Всесоюзной школы по голографии. Л., ЛИЯФ, 1978, с.198-218.
9. Ивакин Е.В., Кицак А.И. Оптика и спектроскопия. 1982, 25, №1, с.99-102.
10. Власов Н.Г., Цитович В.А. // Докл. V Всесоюзной конференции по фотометрии и ее метрологическоыу обеспечению, М., ВНИИОФИ, 1984, с.316.
11. Якимович А.П. "Квантовая электроника", 1984, т.11, №4, с.680-683.
12. Власов Н.Г., Корчажкин С.В., Мацонашвили Р.Б. и др. "Оптика и спектроскопия", 1985, т.59, №4.
13. Сороко Л.М. Основы голографии когерентной оптики, М., Наука, 1972, с.616.
14. Городецкая В.И., Кособурд Т.П., Маркус Ф.А. Оптика и спектроскопия. 1984, т.57, №1, с.139-142.
15. Власов Н.Г., Семенов Э.Г., Соколова Н.Э. // Х II Всесоюзная конференция по высокоскоростной фотографии, фотонике и метрологии быстропротекающих процессов". М., ВНИИОФИ, 1985, с.97.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

