|
|
 |
 |

|
| |
АДАПТИВНОЕ ВОССТАНОВЛЕНИЕ ИЗОБРАЖЕНИЙ
НА ОСНОВЕ КРИТЕРИЕВ ЭНТРОПИЙНОГО ТИПА
А.А.Корниенко
Рассмотрены возможности получения и адаптивной коррекции изображений протяженных объектов в оптических системах видения с управлением излученной волной. Обнаружен эффект "консервации" элементов изображения при использовании известного функционала резкости. Для адаптивного восстановления изображений предложены и исследованы на моделях новые критерии, максимизирующие резкость (интенсивность) и энтропию состоянии излученного поля.
В адаптивных оптических системах видения (АОСВ) с управлением излученной волной восстановление изображений проблематично даже при известной структуре разрешаемого объекта из-за действия механизма "перемножения" изображений /1,2/. В связи с этим перспективным направлением получения и адаптивной коррекции изображений является поиск принципиально новых критериев и алгоритмов адаптации, основанных на введении в максимизируемые функционалы интенсивности информации об амплитудно-фазовом распределении в различных сечениях управляемого поля излучения. В основу конструирования таких критериев могут быть положены физические принципы, обуславливающие эффект "консервации" изображения в АОСВ при максимизации известного функционала резкости (ФР):
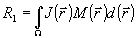 , (1) , (1)
где Ω - внешний контур изображения объекта, состоящего из М разрешаемых блестящих точек с коэффициентами отражения С m, J( 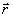 ) - распределение интенсивности образа в плоскости изображения или в некоторой другой плоскости изображающей линзы. Маска ) - распределение интенсивности образа в плоскости изображения или в некоторой другой плоскости изображающей линзы. Маска 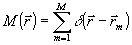 позволяет анализировать интенсивность позволяет анализировать интенсивность 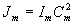 в точках в точках 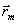 , соответствующих главным максимумам дифракционных изображений блестящих точек /3/, где Im - распределение интенсивности излученного поля в плоскости объекта. , соответствующих главным максимумам дифракционных изображений блестящих точек /3/, где Im - распределение интенсивности излученного поля в плоскости объекта.
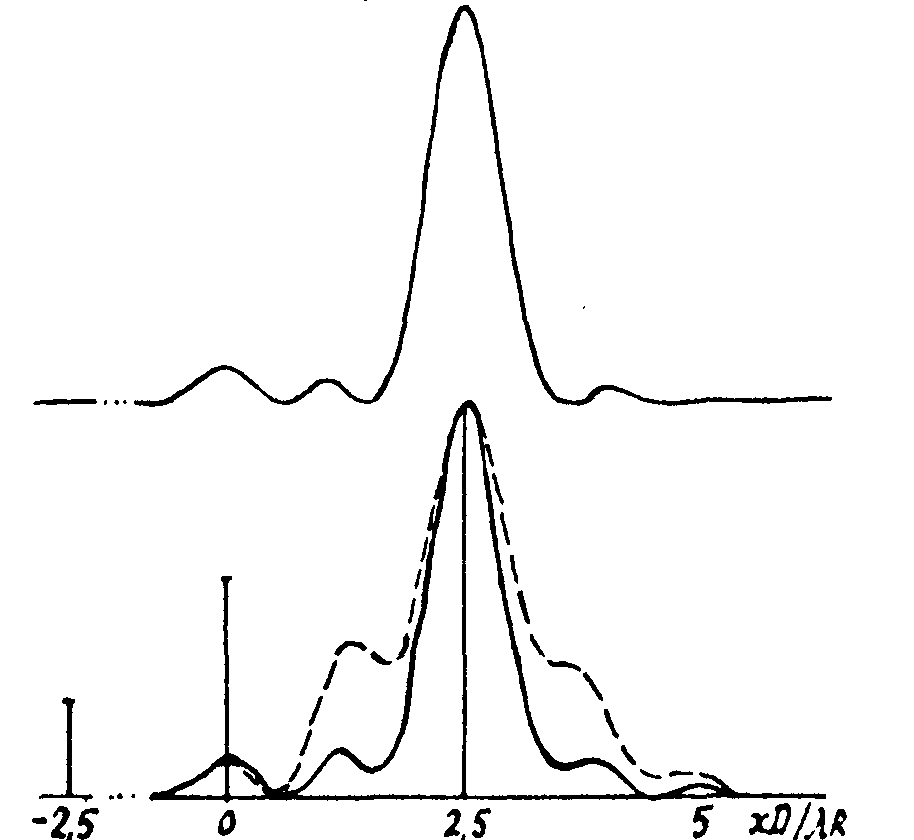
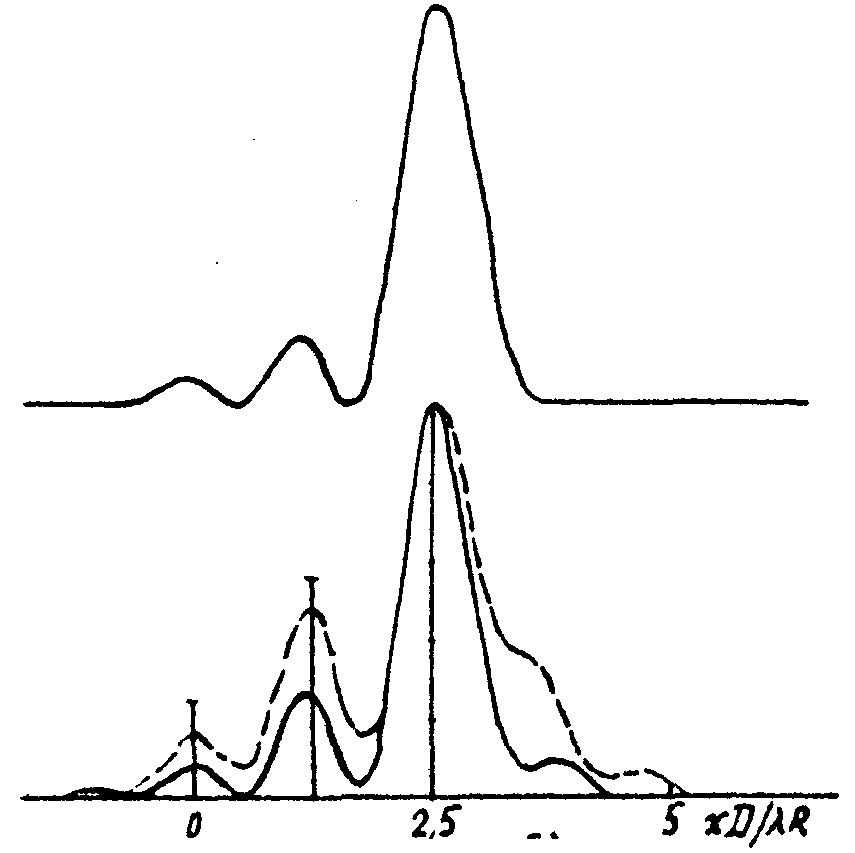
Эффекты конвергенции излученного поля на самой яркой точке и "консервации" элементов изображения в АОСВ при максимизации R1 (после 8 итераций) иллюстрируются рис.1. Адаптивная апертура диаметром D=1,25∙10-4 R (R - расстояние между плоскостями объекта и апертуры, а также "приведенное" фокусное расстояние изображающей линзы) состояла из 25 субапертур. Вертикальными линиями показаны относительные угловые координаты расположения блестящих точек (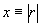 ; a) xmD/λR = -2,5; 0; 2,5 и б) xmD/λR = 0; 1,25; 2,5) и значения коэффициентов их отражения ( ; a) xmD/λR = -2,5; 0; 2,5 и б) xmD/λR = 0; 1,25; 2,5) и значения коэффициентов их отражения (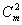 = 0,25; 0,56; 1). Штриховые кривые характеризуют анализируемое распределение интенсивности образа в области Френеля. Эффект конвергенции излученного поля и формирования изображения самой яркой точки сильно выражен при разнесении точек на несколько интервалов разрешения (рис.1а). Для второй конфигурации точек (рис.1б) характерно появление в конвергирующем поле заметных максимумов излучения, подсвечивающих менее яркие точки. В результате в распределении интенсивности образа хорошо подчеркнуты элементы изображения, особенно при анализе R1 в области Френеля. = 0,25; 0,56; 1). Штриховые кривые характеризуют анализируемое распределение интенсивности образа в области Френеля. Эффект конвергенции излученного поля и формирования изображения самой яркой точки сильно выражен при разнесении точек на несколько интервалов разрешения (рис.1а). Для второй конфигурации точек (рис.1б) характерно появление в конвергирующем поле заметных максимумов излучения, подсвечивающих менее яркие точки. В результате в распределении интенсивности образа хорошо подчеркнуты элементы изображения, особенно при анализе R1 в области Френеля.
Наблюдаемый эффект "консервации" изображения физически обусловлен влиянием интерференции дифракционных изображений точек на максимизируемый функционал R 1 в области анализа Ω. Действительно, расположение блестящих точек рис.1б соответствует случаю совпадения главного максимума дифракционного изображения одной точки с наиболее интенсивным вторичным максимумом (его весовой коэффициент относительно главного максимума а2≈0,09 в области Фраунгофера и а2≈0,3 в области Френеля) дифракцион-
ного изображения соседней точки. В этом случае вес интерференционного члена 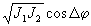 (М=2) в ФР (М=2) в ФР
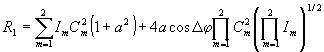 (2) (2)
становится значительным. В отличие от резкостного члена 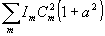 в R1 интерференционный член стремится распределить равномерно интенсивность падающего излучения между блестящими точками, поскольку он достигает максимума при I1=I2 ( в R1 интерференционный член стремится распределить равномерно интенсивность падающего излучения между блестящими точками, поскольку он достигает максимума при I1=I2 (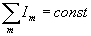 ). ).
Обнаруженный эффект позволяет сформулировать физические принципы построения новых функционалов интенсивности и алгоритмов адаптации, позволяющих восстанавливать изображение в АОСВ. Во-первых, как и традиционные ФР, такой функционал Si должен максимизировать интенсивность поля в области анализа Ω0, которую занимает изображение, а следовательно, "стягивать" энергию излученного поля на объекте 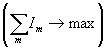 . Во-вторых, он должен "выравнивать" интенсивность падающего на объект поля (с точностью до коэффициента, учитывающего фазовые соотношения), т.е. содержать функционал формы Fi= Fi(I1,...,Im,...IM), который достигает максимума при I1=I2=...=IM и . Во-вторых, он должен "выравнивать" интенсивность падающего на объект поля (с точностью до коэффициента, учитывающего фазовые соотношения), т.е. содержать функционал формы Fi= Fi(I1,...,Im,...IM), который достигает максимума при I1=I2=...=IM и 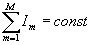 . С позиций теории информации это эквивалентно максимизации энтропии (как меры неопределенности) состояний излученного поля в плоскости объекта. . С позиций теории информации это эквивалентно максимизации энтропии (как меры неопределенности) состояний излученного поля в плоскости объекта.
Таким образом, получение и адаптивная коррекция изображений в АОСВ связаны с максимизацией функционалов интенсивности, сочетающих в себе разностные (энергетические) и энтропийные (информационные) свойства, т.е. функционалов резкости энтропийного типа (ФРЭТ).
Конструируемые ФРЭТ должны отличаться простой технической реализацией и высокой скоростью сходимости созданных на их основе алгоритмов адаптации. Основными задачами при их получении являются поиск функционалов формы Fi, имеющих единственный максимум при I1=...=Im=...Im и 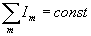 , и наилучших способов объединения функционалов резкости Ri и формы Fj. Используя методы решения экстремальных задач, найдем, , и наилучших способов объединения функционалов резкости Ri и формы Fj. Используя методы решения экстремальных задач, найдем,
что энтропийными свойствами обладает достаточно большой ряд функций Fi:
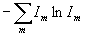 , , 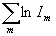 , , 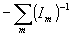 , , 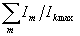 , , 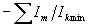
и др.
Практический интерес представляет поиск таких функционалов Fi, которые обладали бы и резкостными свойствами (Fi=Ri=Si). Это, в частности, следующие функционалы:
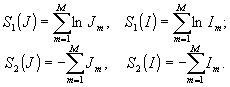
Для адаптивного восстановления изображения являются достаточно эффективными, и комбинированные ФРЭТ будут
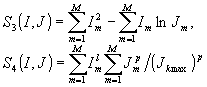
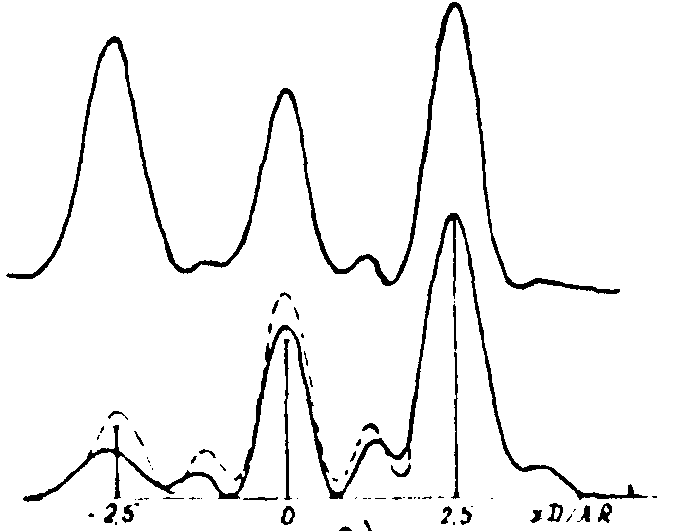
с учетом анализа распределения поля в плоскости изображения и излученного поля в фокальной плоскости линзы ( Im). Высокая эффективность восстановления изображения в АОСВ при использовании ФРЭТ, в частности S1(J), подтверждается результатами моделирования (рис.2). Здесь штриховые кривые характеризуют изображения, получаемые в неискажающей оптической системе при подсветке объекта плоской волной. Для конфигурации точек рис.2б излученное поле в плоскости объекта "выравнено" с учетом интерференционных эффектов.
Функционалы резкости энтропийного типа могут использоваться в адаптивных оптических системах для получения заданных распределений интенсивности, выделения контуров объекта (в изображающих системах с управлением принимаемой волной) и других преобразований изображения.
а)
б)
Рис.1. Установившиеся распределения нормированных интенсивностей излученного поля в плоскости объекта (вверху) и поля в плоскости изображения (внизу) при максимизации функционала резкости R1.
а)
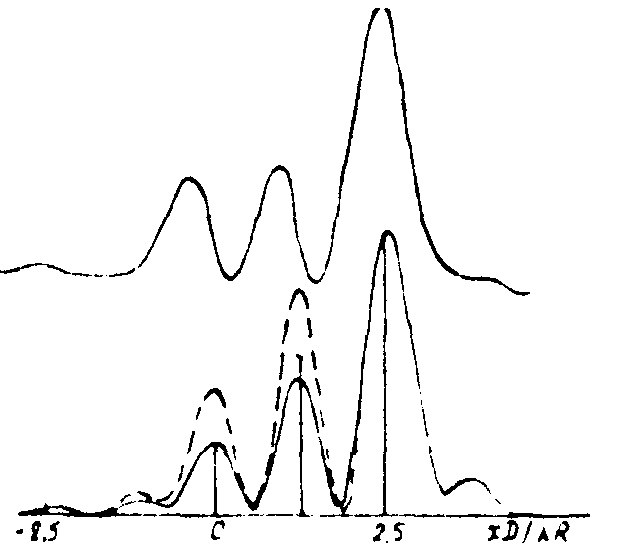
б)
Рис.2. Установившиеся распределения нормированных интенсивностей излученного поля в плоскости объекта (вверху) и поля в плоскости изображения (внизу) при максимизации функционала резкости энтропийного типа S1(J).
Л и т е р а т у р а
1. Waters W.M. IEEE Тrаns. on Aеrоsр. and Electr. Syst., 1970, 6, 4, 503.
2. Хейес К. и др. // "Адаптивная оптика", М., Мир, 1980, с.28.
3. Матвеев И.Н., Сафронов А.Н., Троицкий И.Н., Устинов Н.Д. Адаптация в информационных оптических системах, М ., Радио и связь, 1964.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

