|
|
 |
 |

|
| |
ВЛИЯНИЕ ФОРМЫ ВОЛНОВОГО ФРОНТА
НА РЕЗУЛЬТАТ РАСШИФРОВКИ ИНТЕРФЕРОГРАММ
Н.А.Мальцева, С.П.Пресняков
Экспериментально показано, что погрешность измерения фазы в приближении геометрической оптики, связанная с расходимостью объектной волны, может значительно превосходить поправку на рефракцию при регистрации интерферограмм как в свободном пространстве, так и по схеме сфокусированного изображения. Предложен алгоритм расшифровки результатов интерференционных измерений, учитывающий расходимость объектной волны и расстояние от объекта до плоскости регистрации. Результаты численного моделирования показали, что использование рассматриваемого алгоритма коррекции результатов интерференционных измерений уменьшает погрешность определения распределения показателя преломления более чем на порядок. Предложена оптическая схема получения интерферограмм, свободных от рефракции и расходимости объектной волны.
Среди бесконтактных оптических методов диагностики различных объектов и процессов голографическая интерферометрия занимает одно из ведущих мест /1-4/. Порядки интерференции (номера полос) и их координаты, определенные по интерферограмме, позволяют построить функцию изменения оптической длины пути зондирующего излучения (функцию фазового сдвига φ 0). В приближении прямолинейного распространения лучей величинам фазового сдвига φ0 в плоскости интерферограммы приписываются значения интегралов по прямым от приращения показателя преломления /2/:
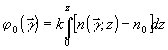 , (1) , (1)
где ось z совпадает с направлением просвечивания, 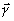 ={x,у}-координаты в плоскости интерферограммы, ={x,у}-координаты в плоскости интерферограммы, 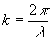 , λ - длина волны зондирующего излучения, , λ - длина волны зондирующего излучения, 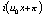 , n0 - показатели преломления оптической неоднородности и окружающей среду, соответственно. Таким образом, расшифровка интерферограмм заключается в решении интегрального уравнения 1-ого рода: , n0 - показатели преломления оптической неоднородности и окружающей среду, соответственно. Таким образом, расшифровка интерферограмм заключается в решении интегрального уравнения 1-ого рода:
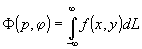 , (2) , (2)
|p|, φ - параметры нормального уравнения прямой L.
В настоящее время существует множество методов решения уравнения (2). Краткая характеристика и сравнение существующих алгоритмов приводится в /5/. К ним относятся прежде всего классические алгебраические методы /6/, метод полиномиальных разложений /7-9/, алгоритмы фурье-синтеза /10-11/, итерационные алгоритмы /12/, а также использование преобразования Радона /13-14/.
Переход к более сложной задаче восстановления распределения показателя преломления при криволинейном распространении зондирующего излучения в настоящее время осуществляется по следующим направлениям.
Во-первых, это учет криволинейности траекторий в приближении геометрической оптики с помощью итерационных схем /15/, т.е. сначала решается задача восстановления распределения показателя преломления в приближении прямолинейного распространения лучей, затем, по полученным значениям рассчитываются траектории и набег фаз вдоль искривленных лучей, делается поправка и т.д. Метод этот достаточно трудоемкий и сходимость его пока не доказана .
Во-вторых, в рамках эйконального приближения получены формулы для вклада рефракции в распределение интерференционных по-
лос на интерферограмме, на основании которых разработаны алгоритмы восстановления распределения показателя преломления с учетом рефракции /16,17 /.
В-третьих, это решение исследуемой задачи на основе идей, используемых в дифракционной томографии /18-20/. В нем решается полное волновое уравнение, либо уравнение Гельмгольца, а в качестве входных данных используется информация о комплексной амплитуде поля, рассеянного объектом. Решение обычно находится с использованием приближения Берна или путем преобразования волнового уравнения в уравнение Риккати (приближение Рытова). Основным недостатком этого перспективного метода для голографической интерферометрии является трудность извлечения из оптического поля информации об его амплитудной и фазовой составляющих.
В-четвертых, это решение волнового уравнения в параболическом приближении с помощью метода плавных возмущений /21/.
Достоинством метода параболического приближения является то, что при некоторых ограничениях на исследуемый объект параболическое уравнение имеет приближенное решение. Действительно, для комплексной амплитуды, записанной в виде:
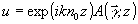 , ,
параболическое уравнение для функции 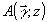 имеет вид /22/: имеет вид /22/:
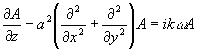 , (3) , (3)
где 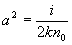 , , 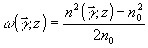 . .
При достаточно медленном изменении 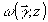 по переменным {х,у} в области радиуса по переменным {х,у} в области радиуса 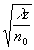 приближенное решение уравнения (3) имеет вид /23/: приближенное решение уравнения (3) имеет вид /23/:
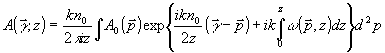 , (4) , (4)
где А 0( 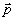 ) - комплексная амплитуда поля при z=0. Выражение (4) является преобразованием Френеля функции ) - комплексная амплитуда поля при z=0. Выражение (4) является преобразованием Френеля функции 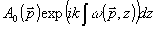 . .
Применяя обратное преобразование Френеля к (4), получаем:
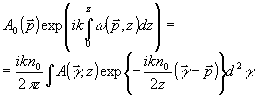 (5) (5)
Таким образом, формула (5) позволяет определить функцию 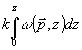 через функции через функции 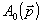 и и 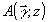 и получить распределение показателя преломления с учетом криволинейности распространения зондирующего излучения. Как показал эксперимент, погрешность измерения фазы в приближении геометрической оптики, связанная с расходимостью объектной волны, может значительно превосходить поправку на рефракцию при регистрации интерферограмм как в свободном пространстве, так и по схеме сфокусированного изображения. Влияние формы волнового фронта объектной волны на фазовый сдвиг иллюстрируется на рис.1, где показаны две голографические интерферограммы одной и той же стеклянной пластины толщиной 1,5 мм. Интерферограммы получены на расстоянии 440 мм от пластины, перед второй экспозицией пластина убиралась из объектного луча. Одна из интерферограмм получена с использованием в объектном луче зрительной трубы. Диаметр луча 50 мм, угол расходимости 1,5∙10-5 рад. При регистрации другой интерферограммы объектный луч расширялся также до диаметра 60 мм системой из двух линз, расходимость луча составляет 3∙10-3 рад. Опорная волна была одинаковой в обоих случаях. и получить распределение показателя преломления с учетом криволинейности распространения зондирующего излучения. Как показал эксперимент, погрешность измерения фазы в приближении геометрической оптики, связанная с расходимостью объектной волны, может значительно превосходить поправку на рефракцию при регистрации интерферограмм как в свободном пространстве, так и по схеме сфокусированного изображения. Влияние формы волнового фронта объектной волны на фазовый сдвиг иллюстрируется на рис.1, где показаны две голографические интерферограммы одной и той же стеклянной пластины толщиной 1,5 мм. Интерферограммы получены на расстоянии 440 мм от пластины, перед второй экспозицией пластина убиралась из объектного луча. Одна из интерферограмм получена с использованием в объектном луче зрительной трубы. Диаметр луча 50 мм, угол расходимости 1,5∙10-5 рад. При регистрации другой интерферограммы объектный луч расширялся также до диаметра 60 мм системой из двух линз, расходимость луча составляет 3∙10-3 рад. Опорная волна была одинаковой в обоих случаях.
На рис.2 штриховой линией показана разность оптических длин пути δN в выделенном горизонтальном сечении интерферограммы. Величина δNmax близка к 1. Поправку на рефракцию δNR

Рис.1. Интерферограммы стеклянной пластины при различных расходимостях объектной волны.
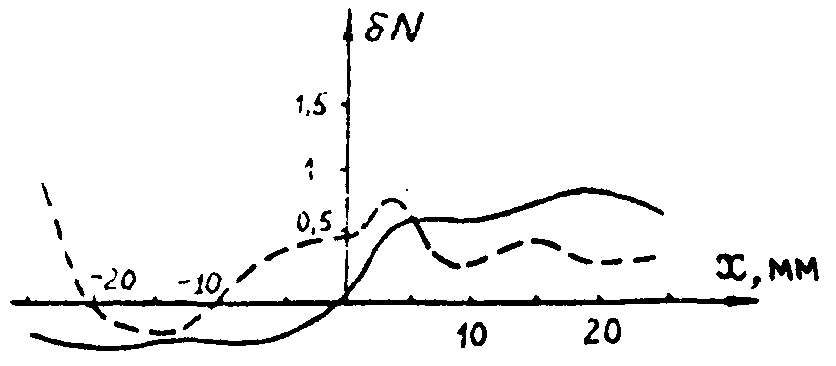
Рис.2. Графики разности оптических длин пути. Ось Х совпадает с горизонтальной линией на интерферограммах рис.1, начало координат в центре интерферограммы.
для этого эксперимента можно посчитать по формуле из /23/:
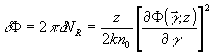 . .
Учитывая, что 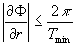 , где Тmin - минимальные расстояния между полосами, получаем: , где Тmin - минимальные расстояния между полосами, получаем:
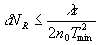 . (6) . (6)
Для λ - 0,63 мкм по формуле (6) для интерферограмм рис.1 находим, что δNR<0,02<<δNmax. Следовательно, в данном случае расходимость объектного луча в большей степени, чем рефракция, влияет на погрешность измерения фазового сдвига. Сплошной кривой на рис.2 показана разность оптических длин пути для голографических интерферограмм сфокусированного изображения. Голограммы стеклянной пластины регистрировались в плоскости ее изображения, фокусное расстояние объектива 210 мм. Для расширения объектного луча использовалась та же оптика, что и в эксперименте, описанном выше. Как видно из рисунка, в этом случае фазовый сдвиг не зависит от расходимости объектной волны только в параксиальной области; функция разности оптических длин пути растет с удалением от параксиальной области, а ее конкретный вид зависят от оптической толщины объекта. Результаты численного моделирования влияния формы волнового фронта зондирующей объектной волны на точность расчета распределения показателя преломления по данным измерения фазы представлены на рис.3. В качестве модели использовалась функция приращения показателя преломления вида:
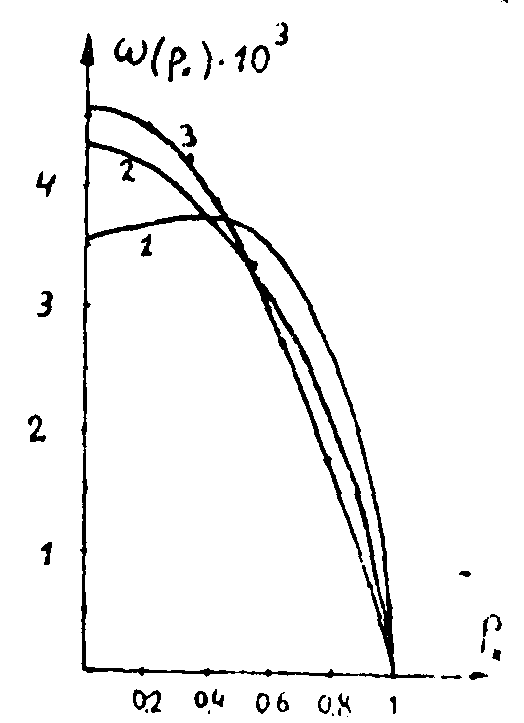
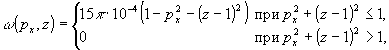
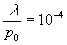 . .
Фаза функции A(x,z) вычислялась по формуле (4) на расстоянии от объекта до плоскости регистрации z=60, для объектной волны с плоским профилем Ψ0(рх)=0 и с гауссовым профилем фазы Ψ0(рх)=20πexp(-4х2), расходимость которой при 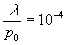 составляет 1,7∙10-3 рад. Полученные таким образом фазы служили исходными данными для вычисления с помощью обращения преобразования Радона, распределения ω(рх,z) при z=1 (кривые 1 и 2 на рис.3). Кривая 3 представляет собой распределение ω(рх,z) при z=1, полученное следующим образом: сначала вычислялась фаза функции на расстоянии z=60 для модели (7) с гауссовым профилем объектной волны; далее, по формуле (5) проводилась коррекция значений фазы и по полученным откорректированным значениям с помощью обращения преобразования Радона было получено распределение ω(px,z) при z=1. Как видно из рисунка 3, подобная коррекция позволила уменьшить погрешность восстановления показателя преломления с 22% до 0,5%. составляет 1,7∙10-3 рад. Полученные таким образом фазы служили исходными данными для вычисления с помощью обращения преобразования Радона, распределения ω(рх,z) при z=1 (кривые 1 и 2 на рис.3). Кривая 3 представляет собой распределение ω(рх,z) при z=1, полученное следующим образом: сначала вычислялась фаза функции на расстоянии z=60 для модели (7) с гауссовым профилем объектной волны; далее, по формуле (5) проводилась коррекция значений фазы и по полученным откорректированным значениям с помощью обращения преобразования Радона было получено распределение ω(px,z) при z=1. Как видно из рисунка 3, подобная коррекция позволила уменьшить погрешность восстановления показателя преломления с 22% до 0,5%.
Отметим, что параметры выполненного численного эксперимента соответствуют реальным ситуация в оптической интерферометрии.
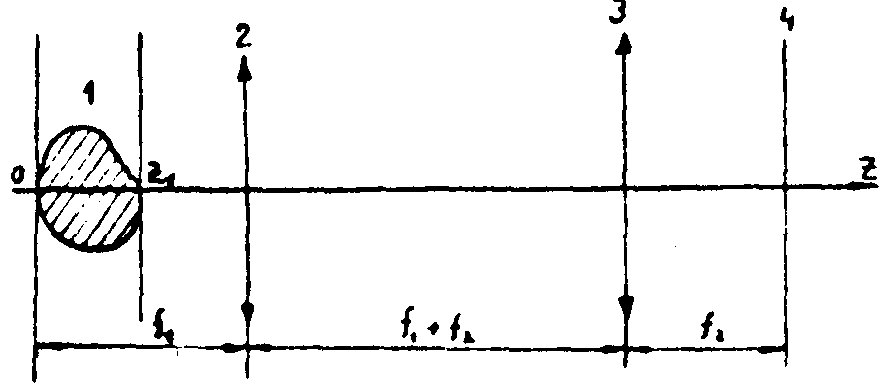
Рис.4. Объектный канал схемы регистрации интерферограмм.
1 - исследуемый объект; 2, 3 - объективы с фокусными расстояниями f1 и f2;
4 - плоскость регистрации интерферограммы.
Для получения интерферограмм, свободных от влияния рефракции и расходимости объектной волны, предлагается фокусирующая система, состоящая из двух объектов с общей фокальной плоскостью (рис.4)..При использовании такой системы интерферограммы получаются не различимы при различных расходимостях объектной волны.
Л и т е р а т у р а
1. Вест Ч. Голографическая интерферометрия. М., 1982. с.504.
2. Островский С.И., Бутусов М.М., Островская Г.В. Голографическая интерферометрия. М., 1977, с.400.
3. Бекетова А.К., Белозеров А.Ф., Березкин А.Н. и др. Голографическая интерферометрия фазовых объектов. Л., 1979, с.232.
4. Гинзбург B.М., Степанов Б.М. Голографические измерения, М., 1981, с.296. Б. Пикалов Б.В., Преображенский И.Г. Вычислительная томография и физический эксперимент. Успехи физических наук. 1983, т.141, №3, с.469.
6. Физические измерения в газовой динамике при горении. Под ред. Ладенбурга Р.У. М., 1967.
7. Maldonado C.D., Caron A.P., Olsen H.N. JOSA, 1965, 55, 10, 1247-1254.
8. Cormack A.M. - J.Appl.Phys., 1963, v.34, p.2722.
9. Пикалов В.В., Преображенский Н.Г. Инженерно-физический журнал, 1977, т.33, с.1042.
10. Bracwell R.N., Riddle A .С. Austrophys J. 1967, 150, 42'7-434.
11. Barrett H.H., Swindell W., Radiological Imaging. The Theory of images/Image Formation, Detection and processing-Acod. Press, 1981.
12. Вишняков Г.Н., Гильман Р.А., Левин Г.Г. Оптика и спектроскопия, 1985, т.58, вып.2, с.406.
13. Пресняков С.П. Оптика и спектроскопия, 1976, т.40, с.124.
14. Melnikova Т.S., Pickalov V.V., In Proc. XV IСРIC Contribut. Papers. Pt.2, Minsk 1981 - P.1003.
15. Soyoung Chc, Vest C.M. Appl.Opt., 1981, v.20 , 16, р.2787-2794.
16. Дубовикова Е.А., Дубовиков М.С. Оптика и спектроскопия. т.58, вып.6, 1985, с.1300.
17. Пикалов В.В., Преображенский Н.Г., Трашкеев С.К. Оптика и спектроскопия, т.58, вып.5, 1985, с.1357.
18. Devaney A.J. Inverse scattering as a form of computed tomography Proceedings SPIE, 1982, v.358, p.10-16.
19. Slaney M., Kak A.C. Diffraction-tomography Proceedings SPIE, 1983, v.413, р.2-10.
20. Pan S.X., Kak A. С. A computational study of reconstruction algorithms for diffraction tomography: interpolation versus filtered backpropagation - IEEE Trans on Acoustics, Speech, Signal Processing, 1933, v.ASSP-31, 5, p.1262-1275.
21. Петров П.Г., Лопатин В.В., Кухта В.Р. Оптика и спектроскопия, 1985, т.58, вып.6, с.1390.
22. Рытов С.М., Кравцов Ю.A., Татарский В.И. Введение в статистическую радиофизику. Случайные поля, М., 1978, ч.11.
23. Мальцева Н.А., Пресняков В.П. Оптика и спектроскопия, т.59, вып.6, 1985, с.1366.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

