|
|
 |
 |

|
| |
ПРЕОБРАЗОВАНИЕ РАДОНА В КОМПЬЮТЕРНОЙ ГОЛОГРАФИИ
Л.Г.Великанова, Н.Г.Преображенский
Рассмотрены простейшие алгоритмы компьютерной голографии, ориентированные на задачи синтеза и реконструкции голограмм двух- и трехмерных объектов. Проанализирована роль преобразования Фурье при реализации этих алгоритмов на ЭВМ. Показано, в силу каких причин для задач компьютерной голографии наряду с преобразованием Фурье оказывается важным также и преобразование Радона, характерное для томографических (интроскопических) постановок задачи. Указаны некоторые следствия взаимосвязи операторов Фурье и Радона, имеющие практическое значение для голографического эксперимента.
1. Как известно, преобразование Радона играет определяющую роль в линейной компьютерной томографии /1-3/. По отношению же к компьютерной (цифровой) голографии принято считать, что основой алгоритмов синтеза и реконструкции голограмм является преобразование Фурье /4-7/. Однако, следует иметь в виду по крайней мере два обстоятельства. Во-первых, томографические принципы как явно, так и неявно все шире внедряются в голографическую технику; достаточно упомянуть о многоракурсной голографической и спекл-интерферометрии, радужных голограммах, приемах получения сечений трехмерных фазовых объектов, а также сечений объемных голограмм /8-10/. Во-вторых, хорошо известно, что сами преобразования Фурье и Радона тесно связаны друг с другом и, в частности, широко распространены способы решения задач томографии при помощи Фурье-алгоритмов /11-12/. В связи с этим пред-
ставляется полезным более обстоятельно, чем это было сделано до сих пор, выяснить роль и место преобразования Радона в задачах компьютерной голографии. В данной работе мы ограничимся рассмотрением лишь простейших задач.
2. Напомним прежде всего процедуры компьютерного синтеза и реконструкции 2 D фурье-голограмм, отличающиеся особенной простотой и единообразием интегральных преобразований.
Выберем в качестве объекта плоский одноцветный транспарант, описываемый комплексным амплитудным коэффициентом пропускания a(x,у). Направим на него плоскую волну, фронт которой параллелен плоскости транспаранта, и запишем выражение для амплитуды поля b(ξ,η) в плоскости (ξ,η), отстоящей от плоскости транспаранта на расстояние z и также параллельной ей /5/:
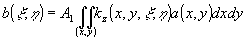 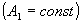 . (1) . (1)
Вид ядра интегрального преобразования kz(x,у;ξ,η) зависит как от z, так и от размеров транспаранта. Ограничиваясь случаем дальней (фраунгоферовой) зоны, возьмем ядро в виде
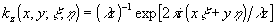 . (2) . (2)
где λ - длина волны, а ξ и η становятся компонентами фурье-спектра; часто их удобно нормировать: ξ1=ξ/λz, η1=η/λz, считая также A1/λz=1. Тогда, вместо (1), получим:
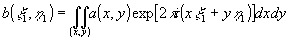 . (3) . (3)
Формула обращения, соответствующая (1), имеет вид:
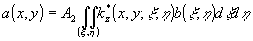 , (4) , (4)
где A2=const, а прежнее ядро заменяется на комплексно сопряженное.
В задаче синтеза искомым математическим образом голограммы следует считать распределение интенсивности
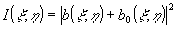 , (5) , (5)
где b0(ξ,η) - вклад амплитуды поля опорной волны. Эту волну можно также выбрать плоской:
b0 (ξ,η)=B0exp(iφ0ξ), B0=const. (6)
Если, кроме этого, в функции b(ξ,η) выделить амплитудный и фазовый множители
b(ξ,η)=B(ξ,η)exp[iφ(ξ,η)], (7)
то, в соответствии с (5), получим
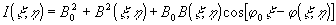 . (8) . (8)
При восстановлении изображения по голограмме нужно также использовать опорную волну (6); тогда в сформированной волне будут содержаться четыре компонента: первые два пропорциональны b(ξ,η) и b*(ξ,η)ехр(2iφ0ξ), а вторые два оказываются чисто шумовыми. Информативные компоненты обусловлены, очевидно, лишь последним слагаемым в правой части (8), содержащим фазовые характеристики.
Мы не касаемся здесь процедур учета неизбежных искажений функции I(ξ,η) за счет интерполяции значений дискретных цифровых отсчетов (задача синтеза), а также искажений, связанных с дискретизацией непрерывной голограммы (задача реконструкции). Обе процедуры реализуются с помощью понятия аппаратной (функции рассеяния точки ФРТ) и в математическом плане сводятся к вычислению двумерной свертки /7/. В свою очередь, это вычисление состоит в расчете прямых и обратных фурье-образов соответствующих функций. Очевидный алгоритм во всех этих преобра-
зованиях - быстрое преобразование Фурье (БПФ).
3. При синтезе голограммы трехмерных (3D) объектов обычно стремятся избежать трудностей последовательного решения возникающей при этом задачи теории поля, вычисляя в том или ином приближении интеграл Френеля-Кирхгофа /13/.
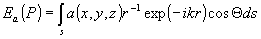 . (9) . (9)
Здесь 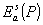 - поле от объекта а(x,y,z) в некоторой точке - поле от объекта а(x,y,z) в некоторой точке 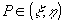 на синтезируемой голограмме; r - расстояние от точки Р до объекта; k=2π/λ - волновое число, S - поверхность, ограничивающая объект, на синтезируемой голограмме; r - расстояние от точки Р до объекта; k=2π/λ - волновое число, S - поверхность, ограничивающая объект, 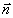 - нормаль к поверхности, - нормаль к поверхности, 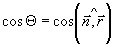 - коэффициент наклона. Интенсивность - - коэффициент наклона. Интенсивность -
I(P)=|Ea+E0|2-|Ea|2+|E0|2+E0Ea*+E0*Ea. (10)
Если опорная волна сферическая, т.е.
Е0(Р)=В0z 0r 0-2 exp(-ikr 0), (11)
где r0 - расстояние от Р до точечного источника, то, применяя ту или иную версию метода интегральных сумм /6/, можно представить (9) в дискретной форме и выразить каждое из четырех слагаемых в (10) в явном алгебраизованном виде. Поскольку формирование действительного или мнимого изображения описывается лишь одним из этих слагаемых, а остальным соответствует "нулевой порядок" (низкочастотные составляющие). то в алгоритме нужно предусмотреть подходящую процедуру фильтрации.
Прямой расчет интеграла Френеля-Кирхгофа громоздок и неконструктивен. Поэтому, как было предложено еще в /4/, гораздо рациональнее сразу преобразовать его либо непосредственно к интегралу Фурье, либо к сверточной форме, когда вычисления также сводятся к подсчету фурье-трансформант. В задачах томографии о подобных случаях принято моделировать 3D объект набором дискретных плоских сечений /3/. Аналогичный прием эффективен и
в компьютерной голографии: в этой ситуации искомое волновое поле приравнивается сумме волновых полей от всех плоскостей /6,13/. Тогда по мере удаления голограммы от объекта, т.е. роста координаты z, расчет Еа(Р) удобно проводить сначала для ближней и дальней областей дифракции Френеля, а затем - в приближении Фраунгофера.
а) Ближнее поле Френеля
В выделенной плоскости объект становится двумерным: а(х,у), а расстояние r=[(ξ-x)2+(η-у)2+z 2] 1/2. Распространяя область интегрирования на всю плоскость (x,у), превращаем (9) в уравнение 2D свертки, решение которого записывается как обратный фурье-образ от произведения прямых фурье-трансформант функций а(x,y) и q(ξ-x,η-y)=r-1exp(-ikr)cosΘ:
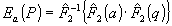 , (12) , (12)
б) Дальнее поле Френеля
Обозначая
β(x,y,z)=exp[-ik(x 2+y 2)/2z]
и преобразуя интеграл Френеля-Кирхгофа /13/, имеем:
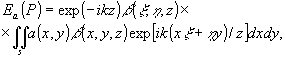 (13) (13)
т.е. задача сводится к вычислению 2 D фурье-образа от произведения {a(x,y)β(x,y,z)} по переменным x и у. Как и выше, Еa(Р) - вклад от одной плоскости.
в) Поле Фраунгофера
В данном случае имеет место вырождение всего пакета сферических волн от совокупности точек-излучателей для выделенного сечения в одну плоскую волну; при этом, очевидно, функция β(x,y,z)
под интегралом (13) стремится к единице, так что
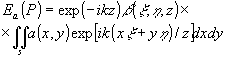 (14) (14)
и мы фактически вернулись к рассмотренному выше случае простейшей фурье-голограммы (3) .
Задача реконструкции 3D объекта по 2D голограмме, описываемой распределением интенсивности I(ξ,n), в расчетном плане очень сходна с только что рассмотренной задачей синтеза.
Если в качестве восстанавливающей использовать волну ( 11), то суммарное поле, формируемое голограммой в области действительного изображения, вновь выражается через интеграл Френеля-Кирхгофа
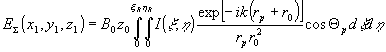 . (15) . (15)
Здесь 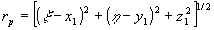 , (x1,y1,z1) -координаты точки реконструкции, , (x1,y1,z1) -координаты точки реконструкции, 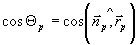 , , 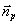 - нормаль к поверхности голограммы, ξR и ηR - апертура голограммы по переменным ξ и η. Для расчета поля в области мнимого изображения достаточно заменить знак при rp на обратный. На хорошо изученных вопросах дискретизации задачи мы здесь не останавливаемся. - нормаль к поверхности голограммы, ξR и ηR - апертура голограммы по переменным ξ и η. Для расчета поля в области мнимого изображения достаточно заменить знак при rp на обратный. На хорошо изученных вопросах дискретизации задачи мы здесь не останавливаемся.
Ясно, что в (15) допустимы те же упрощающие преобразования , которые позволили перевести (9) в формулы (12)-(14). Таким образом, как и в случае 2D транспарантов и их фурье-голограмм, в трехмерной задаче дело сводится к применению прямых и обратных интегральных операторов Фурье и реализации алгоритма БПФ.
4. Покажем теперь, каким образом в задаче компьютерной голографии наряду с преобразованием Фурье появляется преобразование Радона.
В / 6/ и некоторых других работах рассчитывались 3D голо-
граммы от объектов, заданных набором блестящих точек. Как уже отмечалось, использование интеграла Френеля-Кирхгофа есть приближенный путь решения задачи; общая же схема решения должна опираться на волновое уравнение
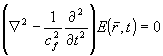 , (16) , (16)
причем скорость распространения волны внутри фазового объекта
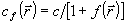 , (17) , (17)
где 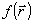 имеет смысл варьируемой в пространстве части показателя преломления среды. Положим далее: имеет смысл варьируемой в пространстве части показателя преломления среды. Положим далее: 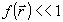 и запишем (16) в виде: и запишем (16) в виде:
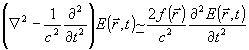 . (18) . (18)
В задаче синтеза голограммы удобно воспользоваться приближением Борна /14/, в соответствии с которым решение выразится суммой:
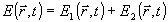 . (19) . (19)
Блестящие точки, совокупностью которых моделируется объект, следует на самом деле считать центрами рассеяния некоторой падающей волны 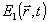 , испускаемой в простейшем случае импульсным точечным излучателем, характеризуемым вектором , испускаемой в простейшем случае импульсным точечным излучателем, характеризуемым вектором 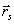 . Согласно первому борновскому приближению поле . Согласно первому борновскому приближению поле 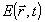 в правой части (18) нужно заменить на в правой части (18) нужно заменить на 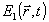 . .
Функция 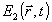 в (19) есть частное решение неоднородного волнового уравнения с известным источниковым членом, находимое стандартным методом функций Грина: в (19) есть частное решение неоднородного волнового уравнения с известным источниковым членом, находимое стандартным методом функций Грина:
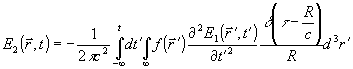 , (20) , (20)
где 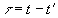 , , 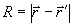 . .
Пусть в момент времени t=t0 источник испускает достаточно короткий импульс сферической формы, для которого
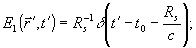 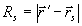 . (21) . (21)
Тогда, согласно (20), отклик Q(t) от этого импульса в точке Р на голограмме выразится в виде
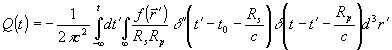 , (22) , (22)
где 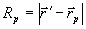 и двумя штрихами обозначена вторая производная от δ -функции Дирака по времени t'. и двумя штрихами обозначена вторая производная от δ -функции Дирака по времени t'.
Ограничимся простейшим приближением Фраунгофера, когда для расстояний Rs и Rp можно оставить лишь первые члены разложений:
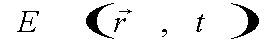 (23) (23)
Отметим, что, упрощая (22). в аргументах δ - функций нужно сохранять по крайней мере два члена разложения; это дает:
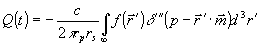 , (24) , (24)
где 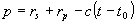 ; ; 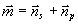 . .
Смысл величин р и 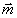 следующий. Скаляр р есть кратчайшее расстояние от выбранного начала отсчета до некоторой плоскости, перемещающейся в пространстве со скоростью с; в начальный момент времени t0 p есть просто сумма расстояний: источник-объект, объект-голограмма. Вектор следующий. Скаляр р есть кратчайшее расстояние от выбранного начала отсчета до некоторой плоскости, перемещающейся в пространстве со скоростью с; в начальный момент времени t0 p есть просто сумма расстояний: источник-объект, объект-голограмма. Вектор 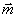 в приближении Фраунгофера можно считать ортом, направленным по нормали к некоторой, пересекающей объект, рассеивающей плоскости, своего рода ''зеркалу", которое эффективно отражает сферическую волну от источ- в приближении Фраунгофера можно считать ортом, направленным по нормали к некоторой, пересекающей объект, рассеивающей плоскости, своего рода ''зеркалу", которое эффективно отражает сферическую волну от источ-
ника к голограмме. Это зеркало есть геометрическое место точек 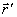 , для которых время распространения короткого импульса вдоль пути , для которых время распространения короткого импульса вдоль пути 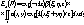 одинаково. одинаково.
Таким образом, формулу (24) можно записать в виде /3/:
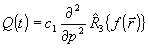 , (25) , (25)
где с 1 - константа, а
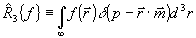 - (26) - (26)
прямое 3D преобразование Радона функции 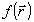 . Отметим, что если вдоль направления . Отметим, что если вдоль направления 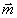 зависимость зависимость 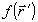 внутри объекта окажется линейной, рассеяния волны на голограмму не происходит, т.е. упомянутое выше "зеркало" перестает быть отражающим. внутри объекта окажется линейной, рассеяния волны на голограмму не происходит, т.е. упомянутое выше "зеркало" перестает быть отражающим.
5. К преобразованию Радона в компьютерной голографии можно прийти и другим путем, воспользовавшись известными соотношениями между плоскими (не обязательно экспоненциальными!) волнами и сферическими средними /15/. Характерная для томографии операция углового усреднения по полусфере (обратное проектирование /3/ осуществляет конверсию плоской волны в сферическую:
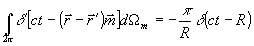 , , 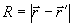 , , 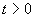 . (27) . (27)
Поэтому при описании перемещения вдоль орта 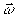 плоского тонкого среза со скоростью с можно исходить из равенства: плоского тонкого среза со скоростью с можно исходить из равенства:
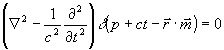 (28) (28)
и решать задачу Коши для всего 3D пространства с начальными условиями:
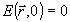 ; ; 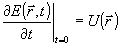 . (29) . (29)
Как известно, зная решение с условиями (29) нетрудно сразу же записать и решение при 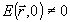 /16/. /16/.
Используя неэкспоненциальный δ-базис (28), с учетом (29) имеем:
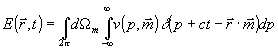 , (30) , (30)
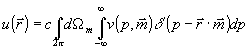 . (31) . (31)
Формулой обращения для (31) служит выражение:
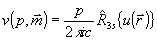 , (32) , (32)
где 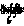 - симметрированный 3D оператор Радона /17/. - симметрированный 3D оператор Радона /17/.
Если теперь подставить (32) и (30) и учесть формулу конверсии (27), то поле 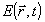 можно будет найти по одной на следующих формул: можно будет найти по одной на следующих формул:
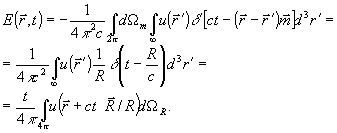 (33) (33)
Далее, конкретизируя геометрию расположения источника, объекта и голограммы, а также свойства объекта, можно по описанной ранее схеме решать задачу компьютерного голографического синтеза.
6. Коснемся в заключение некоторых практически важных аспектов связи преобразований Фурье и Радона. Отметим прежде всего хорошо известное и легко доказываемое операторное соотноше-
ние:
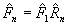 , (34) , (34)
где индекс n указывает на n-ую размерность оператора.
Продемонстрируем на двух примерах роль этого соотношения в компьютерной голографии.
а) Пусть зарегистрирована многоракурсная двухэкспозиционная голограмма двумерного ( n=2) фазового объекта /9/, в результате чего путем стандартной обработки получен набор (числовой массив) оптических разностей хода 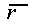 , где , где 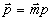 , p - кратчайшее расстояния от начала координат до определенного луча зрения; , p - кратчайшее расстояния от начала координат до определенного луча зрения; 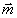 - орт, перпендикулярный этому лучу. Если - орт, перпендикулярный этому лучу. Если 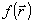 - разность показателей преломления в двухэкспозиционном эксперименте, подлежащая реконструкции, то - разность показателей преломления в двухэкспозиционном эксперименте, подлежащая реконструкции, то 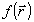 и и 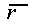 связаны 2D преобразованием Радона: связаны 2D преобразованием Радона:
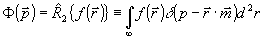 . (35) . (35)
Из (34) следует, что
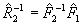 , (36) , (36)
причем прямое преобразование Фурье нужно выполнять вдоль центральных сечений, т.е. линий, проходящих в фурье-плоскости (ξ ,η) χерез начало координат. В компьютерной практике обычно ограничивают двойное интегрирование в фурье-плоскости конечной областью Г, а также, используют частотный фильтр 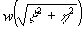 . В результате еще не алгебраизованный алгоритм фурье-синтеза в декартовых координатах приобретает вид: . В результате еще не алгебраизованный алгоритм фурье-синтеза в декартовых координатах приобретает вид:
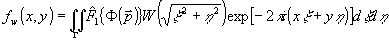 , (37) , (37)
где 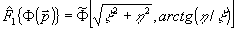 и значком "~" и значком "~"
обозначен 10 фурье-образ функции.
Если сопоставить формулы (37) и (4), причем в последней считать ядро 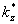 записанным в приближении Фраунгофера, то становится очевидным, что чисто томографическая задача (35) становится эквивалентной задаче компьютерной фурье-голографии при условии: записанным в приближении Фраунгофера, то становится очевидным, что чисто томографическая задача (35) становится эквивалентной задаче компьютерной фурье-голографии при условии:
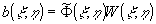 . (38) . (38)
Отметим недавно разработанный в /18/ регуляризующий алгоритм Фурье-реконструкции, дающий при небольших дополнительных затратах вычислительных ресурсов значительный выигрыш в качестве восстановления 2D объекта по голограмме за счет снижения уровня случайной погрешности, "переносимой" из проекционных данных 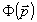 в изображение fw(x,y). При этом необходимое число ракурсов может быть небольшим, что существенно расширяет возможности голографического эксперимента. в изображение fw(x,y). При этом необходимое число ракурсов может быть небольшим, что существенно расширяет возможности голографического эксперимента.
б) Рассмотрим случай n=3 и, обращаясь к формуле (25), найдем в соответствии с (34) фурье-образ импульсного отклика Q(t), фиксируемого на голограмме:
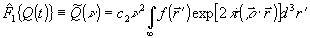 . (39) . (39)
Здесь с 2=const , множитель ν2 отражает наличие в (25) второй производной ¶
2/ ¶
p 2, а интеграл представляет собой 3D- фурье-трансформанту функции рефракции среды 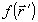 , , 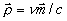 - трехмерный вектор пространственных частот. - трехмерный вектор пространственных частот.
Если при фиксированных положениях источника ( 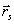 ) и точки детектирования на голограмме ( ) и точки детектирования на голограмме (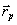 ) осуществить сканирование по частоте ν, то можно передать информацию о тех пространственных частотах объекта, которым соответствует линия вдоль орта m в фурье-облости. Отсюда видно, что, варьируя продолжительностью импульса Δt, исследователь получает возможность менять информационное содержание сигналов, посылаемых 3D фазовым объектом на голограмму в результате рассеяния сферической ) осуществить сканирование по частоте ν, то можно передать информацию о тех пространственных частотах объекта, которым соответствует линия вдоль орта m в фурье-облости. Отсюда видно, что, варьируя продолжительностью импульса Δt, исследователь получает возможность менять информационное содержание сигналов, посылаемых 3D фазовым объектом на голограмму в результате рассеяния сферической
волны. Например, беря δ-импульс (21), которому соответствует полный спектр временных частот, можно в одном измерении получать весь набор луч-сумм, характеризуемых ортом 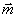 , т.е. полную томографическую проекцию. , т.е. полную томографическую проекцию.
Из рассматриваемых примеров видно, что даже элементарный анализ самой простой формы операторной связи преобразований Фурье Радона в виде (34) позволяет прийти к практически полезным выводам относительно возможностей компьютерного голографического эксперимента. В действительности, связь преобразования Фурье через потенциалы Рисса с теми преобразованиями интегральной геометрии, которые постоянно используются в современной томографии, существенно глубже и многограннее /19,20/. Последовательный учет этой связи, по-видимому, сможет привести к ряду новых следствий, представляющих практический интерес как для голографии, так и для томографии.
Л и т е р а т у р а
1. Хермен Г. Восстановление изображений по проекциям (Основы реконструктивной томографии), М., Мир, 1983, с.350.
2. Пикалов В.В., Преображенский Н.Г. Вычислительная томография и физический эксперимент. Успехи физических наук, 1983, с.141, №3, с.469-498.
3. Barrett H.H. The Radon transform and its applications.-
In: Progress in Optics, ed.E.W оlf, Elsevier, v.21, 1934, p.217-286.
4. Lesem L., Hilrsch P., Jordan J.Comutor synthesis of holograms for 3-d display,-Communications of A.C.M., 1968, v.7, 10, p.661-674.
5. Huang I.S. et al. Digital Holography- Proceedings of the IEEE 1971, v.59, 9, р.1335-1345.
6. Голография. Методы и аппаратура. Под ред.В.М.Гинзбург и Б.М.Степанова. М., Советское радио, 1974, с.376.
7. Ярославский Л.П., Мерзляков Н.С. Цифровая голография. М., Наука, 1982.
8. Денисюк Ю.H. Некоторые проблемы и перспективы голографии в трехмерных средах. // Оптическая гслография, под ред. Г.Колфилда, М., Мир, 1982, т.2, с.691-729.
9. Ч.Вест. Голографическая интерферометрия. М., Мир, 1982, с.504.
10. Козанне А., Флере Ж., Мэтр Г., Руссо М. Оптика и связь, М ., Мир, 1984, с.504.
11. Гельфанд И.М., Граев М.И., Виленкин Н.Я. Интегральная геометрия и связанные с ней вопросы теории представлений. М., ГИМФЛ, 1962, с.656.
12. Луитт P.M. Алгоритмы реконструкции с использованием интегральных преобразований. ТИИЭР, 1983, с.71, №3, с.125-147.
13. Кольер Р. Беркхарт К., Лин Л. Оптическая голография. М., Мир, 1973. с.686.
14. Борн М., Вольф Э. Основы оптики. М., Наука, 1970, с.856.
15. Йон Ф. Плоские волны и сферические средние в применении к дифференциальным уравнениям с частными производными. М., ИЛ, 1958, с.156.
16. Курант Р. Уравнения с частными производными. М., Мир, 1964, с.830.
17. Barrett H.H. Dipole-sheet transform.- J.Opt.Soc.Amer., 1982, v.72. 4, р.463-475.
18. Воскобойников Ю.Е., Пиклов В.В., Седельников А.И. Регуляризующий алгоритм Фурье-реконструкции. II-ой Всесоюзный симпозиум по вычислительной томографии. Куйбышев, 1985, с 40-41.
19. Smith K.I., Keinert I. Mathematical foundations of computed tomography.- Appl.Optics., 1985, v.24, 23, p.3950-3957.
20. Хелгасон С. Преобразование Радона, М., Мир, 1983, с. 150.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

