|
|
 |
 |

|
| |
ИТЕРАЦИОННЫЕ МЕТОДЫ ВОССТАНОВЛЕНИЯ ФАЗЫ
ПО РАСПРЕДЕЛЕНИЮ ИНТЕНСИВНОСТИ
М.А.Воронцов, В.П.Сивоконь
Проблема восстановления фазы световой волны является одной из классических задач оптики. Обсуждению тех или иных аспектов этой проблемы посвящено большое количество работ /1,2/. В классической постановке задачи фазовый профиль требуется найти по единственному распределению интенсивности. Несмотря на существующие дисперсионные соотношения, связывающие интенсивность и фазу поля (преобразование Гильберта) непосредственно воспользоваться этой связью в практических задачах оказывается довольно сложно /2,3/. По этой причине широкое распространение получил альтернативный подход к восстановлению фазы, приводящий к итерационным методам её восстановления. Рассмотрим этот подход подробнее.
Пусть на вход некоторой оптической системы поступает монохроматическая световая волна с комплексной амплитудой A(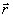 ,z): ,z):
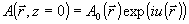 , (1) , (1)
где 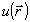 - подлежащая определению фазовая функция, - подлежащая определению фазовая функция, 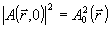 - распределение интенсивности светового поля на входе в систему, которое предполагается известным, - распределение интенсивности светового поля на входе в систему, которое предполагается известным, 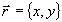 - декартовы координаты в плоскости, перпендикулярной оптической оси системы oz. В выходной плоскости системы регистрируется некоторое распределение интенсивности - декартовы координаты в плоскости, перпендикулярной оптической оси системы oz. В выходной плоскости системы регистрируется некоторое распределение интенсивности  [4]. Вид этого распределения зависит от фазы поля [4]. Вид этого распределения зависит от фазы поля 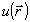 во входной плоскости и характера преобразования входного поля в оптической системе. Задача заклю- во входной плоскости и характера преобразования входного поля в оптической системе. Задача заклю-
чается в определении 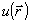 на основе анализа распределений интенсивности на основе анализа распределений интенсивности 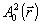 , , 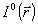 во входной и выходной плоскостях системы. во входной и выходной плоскостях системы.
Одним из первых практических алгоритмов восстановления фазы был алгоритм Гершберга-Сакстона, предложенный в 1972 году /5/. Этот алгоритм является итерационным, т.е. фаза 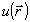 является пределом последовательности оценок фазовых функций является пределом последовательности оценок фазовых функций 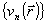 , определяемых в процессе итераций по некоторому правилу. Процедура определения фазы , определяемых в процессе итераций по некоторому правилу. Процедура определения фазы 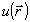 в алгоритме Гершберга-Сакстона была предложена, исходя из эвристических соображений. Позднее было показано /6/, что при малых отклонениях начальной фазовой функции в алгоритме Гершберга-Сакстона была предложена, исходя из эвристических соображений. Позднее было показано /6/, что при малых отклонениях начальной фазовой функции 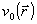 итерационного процесса от точного решения итерационного процесса от точного решения 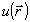 , алгоритм эквивалентен градиентной процедуре минимизации функционала ошибки , алгоритм эквивалентен градиентной процедуре минимизации функционала ошибки
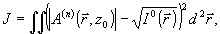 (2) (2)
где 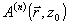 - комплексная амплитуда поля в выходной плоскости z=z0 на n-ой итерации, соответствующая фазовой функции - комплексная амплитуда поля в выходной плоскости z=z0 на n-ой итерации, соответствующая фазовой функции 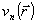 . Более того, в процессе итераций значение функционала J не возрастает /5/. В целом же вопрос о математическом обосновании алгоритма Гершберга-Сакстона, его эффективности остается открытым. Помимо этого, чисто теоретического вопроса, белее важным являются практические потребности как-то модифицировать алгоритм. Дело в том, что алгоритм Гершберга-Саксона хорошо сходится лишь при достаточно малых отклонениях начальной фазы от искомой функции . Более того, в процессе итераций значение функционала J не возрастает /5/. В целом же вопрос о математическом обосновании алгоритма Гершберга-Сакстона, его эффективности остается открытым. Помимо этого, чисто теоретического вопроса, белее важным являются практические потребности как-то модифицировать алгоритм. Дело в том, что алгоритм Гершберга-Саксона хорошо сходится лишь при достаточно малых отклонениях начальной фазы от искомой функции 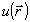 . Кроме того, метод оказался чувствительным к различного рода шумам, неизбежным при измерении интенсивности. В результате наличие сравнительно малых ошибок в определении интенсивности приводит к расходимости алгоритма. Другой, практически важный вопрос связан с самой постановкой задачи восстановления фазы. В практических задачах часто имеется возможность зарегистрировать не два, а, вообще говоря, несколько распределений интенсивности. Алгоритм Гершберга-Сакстона не дает рецепта, как воспользоваться этой дополнительной информацией. . Кроме того, метод оказался чувствительным к различного рода шумам, неизбежным при измерении интенсивности. В результате наличие сравнительно малых ошибок в определении интенсивности приводит к расходимости алгоритма. Другой, практически важный вопрос связан с самой постановкой задачи восстановления фазы. В практических задачах часто имеется возможность зарегистрировать не два, а, вообще говоря, несколько распределений интенсивности. Алгоритм Гершберга-Сакстона не дает рецепта, как воспользоваться этой дополнительной информацией.
В настоящей работа дается математическое обоснование алгоритма Гершберга-Сакстона. Показано, что он является реализацией метода условного градиента минимизации функционала J. На основе проведенного анализа предложены новые алгоритмы восстановления фазы по любому числу зарегистрированных распределений интенсивности. Оказалось, что такие алгоритмы позволяют восстанавливать фазовую функцию при значительном уровне помех.
Преобразование светового поля 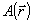 в системе будем описывать некоторым линейным оператором G: в системе будем описывать некоторым линейным оператором G: 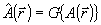 , где , где 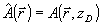 - комплексная амплитуда поля в выходной плоскости прибора. Будем считать, что при распространении волны через оптическую систему ее энергия W сохраняется, т.е. W=(A,A)= - комплексная амплитуда поля в выходной плоскости прибора. Будем считать, что при распространении волны через оптическую систему ее энергия W сохраняется, т.е. W=(A,A)=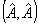 , где (f,g) означает скалярное произведение функций: , где (f,g) означает скалярное произведение функций: 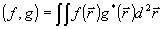 (интегрирование ведется в бесконечных пределах). Легко показать, что из сохранения энергии W следует унитарность оператора: (интегрирование ведется в бесконечных пределах). Легко показать, что из сохранения энергии W следует унитарность оператора: 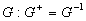 (сопряженный оператор равен обратному). Введенные ограничения на характер преобразования поля в оптической системе характерны для большинства оптических приборов, не содержащих внутренних диафрагм или других поглощающих энергию элементов. В математическом плане задача восстановления фазы сводится к решению нелинейного уравнения: (сопряженный оператор равен обратному). Введенные ограничения на характер преобразования поля в оптической системе характерны для большинства оптических приборов, не содержащих внутренних диафрагм или других поглощающих энергию элементов. В математическом плане задача восстановления фазы сводится к решению нелинейного уравнения:
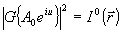 , (3) , (3)
Как правило, задача (3) является некорректной. При наличии шумов, неизбежных при регистрации интенсивности, уравнение (3) может вообще не иметь решения. Вопрос о единственности решения уравнения (3) достаточно сложен и в данной работе не рассматривается (см., например, /2,7-9/).
Будем искать фазовую функцию 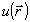 из условия минимума некоторого функционала J, характеризующего отличие измеренного значения из условия минимума некоторого функционала J, характеризующего отличие измеренного значения 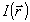 в выходной плоскости системы от некоторого вспомогательного распределения в выходной плоскости системы от некоторого вспомогательного распределения 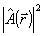 . Конкретный вид функционала J может быть самым разнообразным. Выберем, напри- . Конкретный вид функционала J может быть самым разнообразным. Выберем, напри-
мер, его в виде (2)
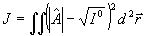 . (4) . (4)
Вспомогательное распределение 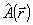 рассчитывается по известной амплитуде поля во входной плоскости следующим образом: рассчитывается по известной амплитуде поля во входной плоскости следующим образом: 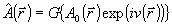 , где , где 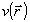 - некоторая оценка искомой фазовой функции - некоторая оценка искомой фазовой функции 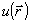 . Задачу восстановления фазы будем считать решенной, если удастся найти такую функцию . Задачу восстановления фазы будем считать решенной, если удастся найти такую функцию 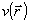 , при которой функционал J достигает минимального значения. Фактически речь идет об определении фазовой функции, с помощью которой наилучшим образом (в смысле критерия J) воспроизводится зарегистрированное распределение интенсивности , при которой функционал J достигает минимального значения. Фактически речь идет об определении фазовой функции, с помощью которой наилучшим образом (в смысле критерия J) воспроизводится зарегистрированное распределение интенсивности 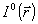 . Воспользуемся градиентной процедурой минимизации функционала J. Наилучшая оценка фазы . Воспользуемся градиентной процедурой минимизации функционала J. Наилучшая оценка фазы 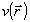 является пределом последовательности оценок фазовых функций является пределом последовательности оценок фазовых функций 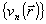 определяемых согласно тому или иному градиенту методу, например: определяемых согласно тому или иному градиенту методу, например:
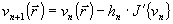 , (5) , (5)
где hn - длина шага метода, 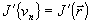 - градиент функционала на n-ой итерации. Начальная оценка - градиент функционала на n-ой итерации. Начальная оценка 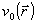 выбирается произвольным образом. Найдем выражение для градиента функционала J. Для этого рассмотрим приращение ΔJ, вызванное малым изменением фазы выбирается произвольным образом. Найдем выражение для градиента функционала J. Для этого рассмотрим приращение ΔJ, вызванное малым изменением фазы 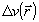 . С точностью до членов второго порядка малости относительно приращения поля . С точностью до членов второго порядка малости относительно приращения поля 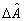 , получим , получим
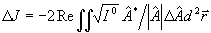 . (6) . (6)
Введем функцию
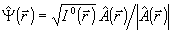 , (7) , (7)
тогда вместо (6) запишем 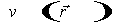 . Используя приведенные выше свойства оператора G, найдем: . Используя приведенные выше свойства оператора G, найдем:
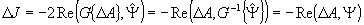 , (8) , (8)
где
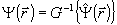 . (9) . (9)
В силу ( 1) 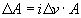 , поэтому для градиента функционала получаем окончательное выражение: , поэтому для градиента функционала получаем окончательное выражение:
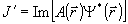 . (10) . (10)
Одним из наиболее эффективных градиентных методов является метод условного градиента /4/. В нем очередная оценка фазы на n-ой итерации определяется из условия минимума приращения ΔJ (8), который, как нетрудно показать, достигается при vn+1=φn, где φn=argΨ(n) - фаза функции Ψ на n-ой итерации.
Рассмотрим некоторые примеры использования предложенного подхода. Пусть оптическая система представляет собой тонкую линзу с фокусным расстоянием F. Пусть также плоскость регистрации расположена на некотором расстоянии z<F от апертуры линзы. Оператор G описывает в этом случае преобразование Френеля:
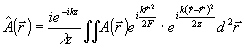 . (11) . (11)
Рассмотренная выше процедура минимизации функционала J (4) методом условного градиента оказывается в этом случае эквивалентной алгоритму Гершберга-Сакстона. Тем самым рассмотренный подход к фазовой проблеме позволяет дать строгое обоснование этого алгоритма, выявляет его градиентный характер.
В практических задачах часто имеется возможность зарегистрировать сразу несколько распределений интенсивности Ik(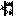 ) (набор изображений), например, в плоскостях, расположенных на расстояниях z=zk, k=1,...,NI от входной плоскости системы (линзы). Стандартные алгоритмы восстановления фазы, как отмеча- ) (набор изображений), например, в плоскостях, расположенных на расстояниях z=zk, k=1,...,NI от входной плоскости системы (линзы). Стандартные алгоритмы восстановления фазы, как отмеча-
лось, не позволяют воспользоваться этой дополнительной информацией. На основе изложенного подхода сравнительно просто построить алгоритмы восстановления фазы по любому числу NI зарегистрированных распределений интенсивности. С этой целью рассмотрим функционал
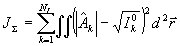 , (12) , (12)
представляющий собой естественное обобщение функционала (4) и учитывающий отклонение вспомогательного распределения интенсивности 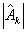 от зарегистрированного в каждой из плоскостей регистрации. Не сложно показать, что градиент функционала от зарегистрированного в каждой из плоскостей регистрации. Не сложно показать, что градиент функционала 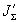 также определяется выражением (10), если при этом функция также определяется выражением (10), если при этом функция 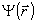 имеет вид: имеет вид:
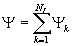 ; ; 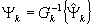 ; ; 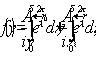 (13) (13)
(оператор Gk описывает распространение поля до плоскости регистрации z=zk).
Приведем некоторые примеры численного исследования рассмотренных алгоритмов. Рассмотрим линзу с радиусом апертуры b и фокусным расстоянием F. Фазовая функция 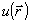 во входной плоскости задавалась в виде во входной плоскости задавалась в виде
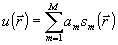 , , М=9, (14)
где 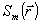 - полиномы Цернике, которые нормированы так, что - полиномы Цернике, которые нормированы так, что 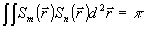 . При этом среднеквадратичное отклонение σ фазы . При этом среднеквадратичное отклонение σ фазы 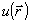 от плоской составляет, как не сложно показать, от плоской составляет, как не сложно показать, 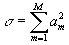 . Явный вид нормированных полиномов Цернике . Явный вид нормированных полиномов Цернике 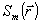 приведен, например, в работе /10/. Аберрационные коэффициенты приведен, например, в работе /10/. Аберрационные коэффициенты 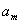 характеризуют диапазон изменения фазовой функции характеризуют диапазон изменения фазовой функции 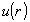 . Амплитуду волны во входной плоскости . Амплитуду волны во входной плоскости 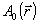 будем считать постоянной: будем считать постоянной: 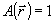 , , 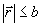 . Все коэффи- . Все коэффи-
циенты полагались одинаковыми и равными am=a, m=1,...,M. Рассматривались три случая: 1 - малый диапазон изменения фазы 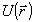 (а=0,05 λ - слабые аберрации, максимальное по апертуре изменение фазы Δ=maxU-minU=1,06λ), 2 - аберрации средней силы (a=0,15 λ, Δ=3,2λ), 3 - сильные аберрации (a=0,25λ, Δ=5,3λ). Распределение интенсивности в плоскостях z=zk рассчитывалось по формуле (11). (а=0,05 λ - слабые аберрации, максимальное по апертуре изменение фазы Δ=maxU-minU=1,06λ), 2 - аберрации средней силы (a=0,15 λ, Δ=3,2λ), 3 - сильные аберрации (a=0,25λ, Δ=5,3λ). Распределение интенсивности в плоскостях z=zk рассчитывалось по формуле (11).
На рис.1 приводятся результаты восстановления фазы для случая
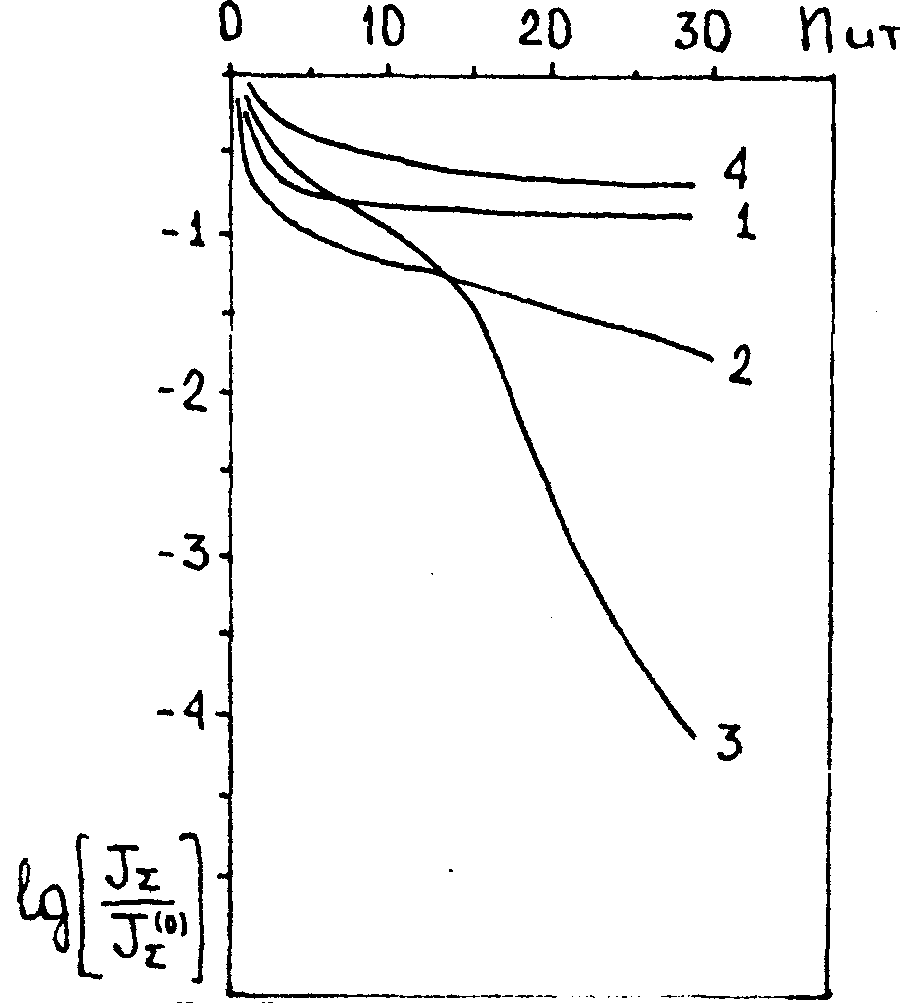
Рис.1. Динамика изменения критерия JΣ при его минимизации методом условного градиента в итерационном процессе восстановления фазы по набору изображений, зарегистрированных на расстояниях {Lk}:
1 - L=∞, 2 - L=0,1, 3 - L={0,1∞}, 4 - L={0,02, ∞}
а = 0 ,15 λ по набору изображений. Рисунок отражает динамику изменения критерия JΣ при его минимизации методом условного градиента. Расстояние до плоскости регистрации zk удобно характеризовать безразмерными величинами, Lk, связанными с zk - соотношениями:
zk=F∙(1-F/(F+LLg)).
где Lg=0,5kb2 - дифракционная длина для заданного размера апертуры линзы b. При этом фокусу линзы z=F соответствует значение L=∞. Из рисунка видно, что использование всего двух изображений (L={0,1, ∞}, кривая 3) позволяет существенно ускорить сходимость процедуры по сравнению с восстановлением фазы по единственному распределению интенсивности (L=∞, кривая 1 и L = 0,1, кривая 2). Добавление третьей плоскости регистрации уже слабо улучшает эффективность восстановления.
Обработка набора из двух изображений ( L={0,1 ,∞}) позволяет существенно расширить и диапазон восстановления. Теперь удается восстанавливать фазу, обладающую сравнительно сильными аберрациями (a=0,25 λ). При этом за 75 итераций критерий JΣ уменьшается почти на 5 порядков (точность восстановления, оцениваемая как максимальное по апертуре отличие оценки фазы 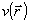 от ее точного значения от ее точного значения 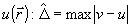 составляет 0,0045λ). Отметим, что в традиционных схемах восстановления по одной плоскости регистрации (типа алгоритма Гершберга-Сакстона) удается восстанавливать фазу, обладающую значительно меньшими аберрациями (a=0,1λ для плоскости регистрации, лежащей в фокусе линзы L=∞, и a=0,15 λ для плоскости с L=0,1). составляет 0,0045λ). Отметим, что в традиционных схемах восстановления по одной плоскости регистрации (типа алгоритма Гершберга-Сакстона) удается восстанавливать фазу, обладающую значительно меньшими аберрациями (a=0,1λ для плоскости регистрации, лежащей в фокусе линзы L=∞, и a=0,15 λ для плоскости с L=0,1).
Вместе с тем, эффективность восстановления фазы и по двум распределениям интенсивности также может оказаться невысокой, если плоскости регистрации выбраны неудачно (рис.1, кривая 4). Это обстоятельство поясняет рис.2, где приведены распределения интенсивности 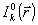 для входного поля с сильными аберрациями (а=0,25 λ) волнового фронта, зарегистрированные на различием расстоянии Lk от апертуры линзы: L1=0,01, для входного поля с сильными аберрациями (а=0,25 λ) волнового фронта, зарегистрированные на различием расстоянии Lk от апертуры линзы: L1=0,01,
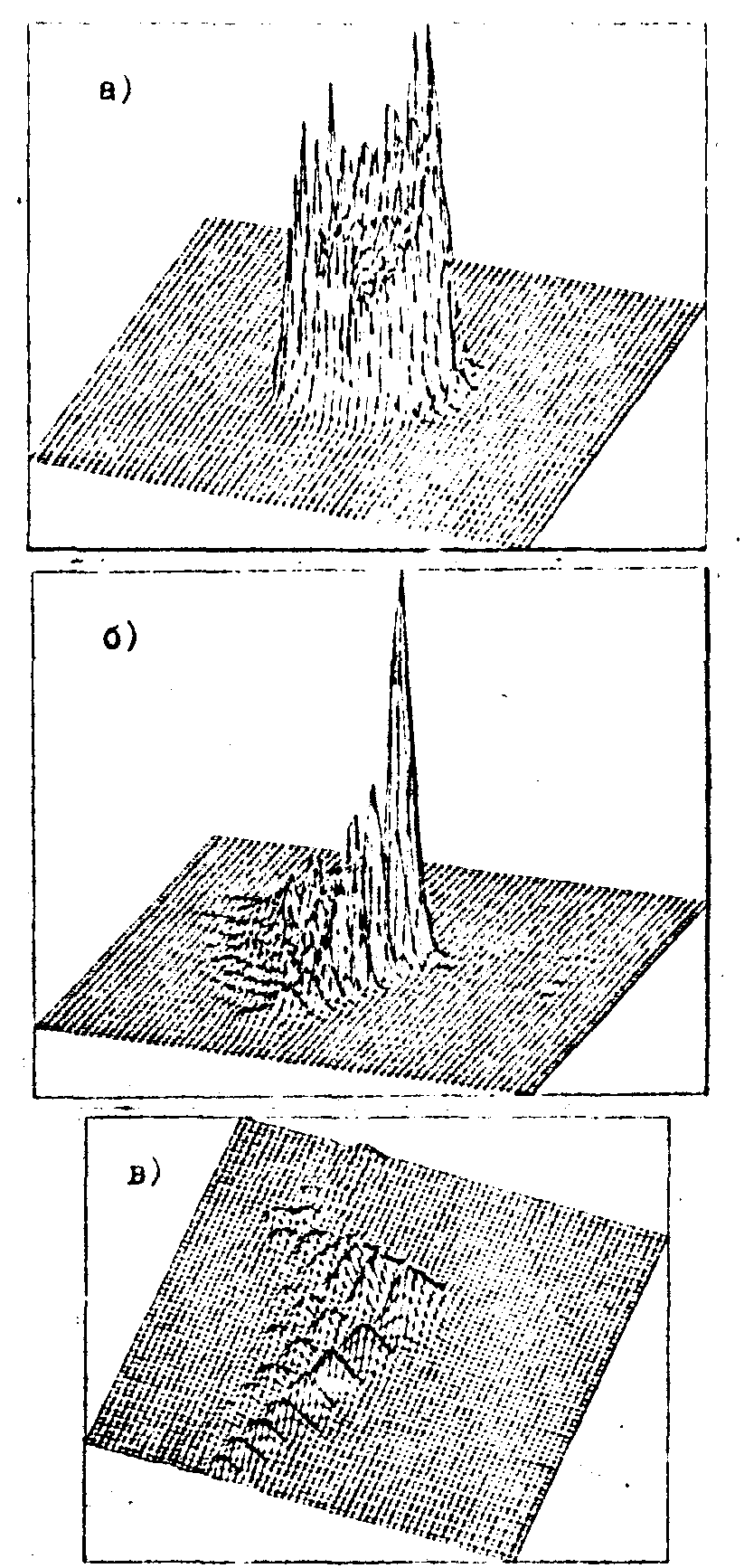
Рис.2.
L2=0,1 и L3=∞ (фокус линзы). Как видно из рисунка, распределение интенсивности 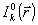 наиболее чувствительно к фазе входного поля в фокальной плоскости (L=∞). При сильных аберрациях это распределение имеет сложный нелокальный характер и резко отличается от соответствующего распределения при отсутствии аберраций. Это, по-видимому, и приводит к отсутствию сходимости итерационной процедуры восстановления. Использование еще одной плоскости регистрации, лежащей в зоне слабой дифракции ( L=0,01) не изменяет ситуацию, поскольку распределение интенсивности в этой плоскости слабо зависит от фазы входного поля. Улучшение сходимости может наступить, если вторая плоскость регистрации будет расположена в зоне умеренного проявления дифракционных эффектов (L=0,1), что и наблюдалось в численных примерах (см.рис.1, кривая 3). По мере приближения оценки фазы наиболее чувствительно к фазе входного поля в фокальной плоскости (L=∞). При сильных аберрациях это распределение имеет сложный нелокальный характер и резко отличается от соответствующего распределения при отсутствии аберраций. Это, по-видимому, и приводит к отсутствию сходимости итерационной процедуры восстановления. Использование еще одной плоскости регистрации, лежащей в зоне слабой дифракции ( L=0,01) не изменяет ситуацию, поскольку распределение интенсивности в этой плоскости слабо зависит от фазы входного поля. Улучшение сходимости может наступить, если вторая плоскость регистрации будет расположена в зоне умеренного проявления дифракционных эффектов (L=0,1), что и наблюдалось в численных примерах (см.рис.1, кривая 3). По мере приближения оценки фазы 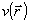 к ее точному значению к ее точному значению 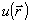 , основной вклад в восстановление фазы начинает вносить фокальная плоскость регистрации, которая и обеспечивает необходимую точность. , основной вклад в восстановление фазы начинает вносить фокальная плоскость регистрации, которая и обеспечивает необходимую точность.
Использование нескольких плоскостей регистрации позволяет также значительно повысить устойчивость процедуры восстановления по отношению к аддитивному шуму в зарегистрированной интенсивности. Это связано, по-видимому, с некоторым эффективным усреднением шума, которое происходит при обработке набора изображений. В таблицу сведены результаты восстановления волнового фронта при наличии шума в каждом из зарегистрированных распределений интенсивности 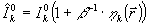 , k=1,...,N1, где , k=1,...,N1, где 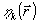 - равномерно-распределенная на интервале [0,1] случайная величина: - равномерно-распределенная на интервале [0,1] случайная величина: 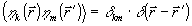 , β - отношение сигнал/шум, , β - отношение сигнал/шум, 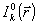 - неискаженное изображение. - неискаженное изображение.
На практике большой интерес представляет задача определения некоторого конечного числа M аберрационных коэффициентов волнового фронта am, m=1,...,N1 непосредственно по распределению интенсивности 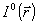 (или набору распределений (или набору распределений 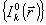 ) без предварительного восстановления самой фазы ) без предварительного восстановления самой фазы 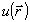 . В таких задачах использование градиентных методов . В таких задачах использование градиентных методов
Таблица
Восстановление фазы по набору изображений, искаженных аддитивным дельта-коррелированным шумом регистрации, для сравнительно
слабых аберраций волнового фронта (а=0,1 λ)
|
Число плоскостей регистрации
N1 |
Координаты плоскостей регистрации {Lk} |
Отношение сигнал/шум
β |
Выполненное число
итераций
n |
Достигнутое качество восстановления
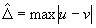
|
|
1*)
2
3
|
{∞}
{0.1, ∞}
{0.1, 0.5, ∞} |
1
0.33
0.1 |
30
28
24 |
0.045λ
0.048λ
0.049λ |
*) - приведены результаты для слабых аберраций волнового фронта (a=0.05λ).
дает особо значительные преимущества. В численных расчетах подлежащая анализу фаза 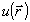 выбиралась аналогично (14). Для определения аберрационных коэффициентов am использовался градиентный алгоритм: выбиралась аналогично (14). Для определения аберрационных коэффициентов am использовался градиентный алгоритм:
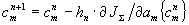 , ,
где 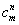 - оценка аберрационных коэффициентов на n-ом шаге итерационного процесса, - оценка аберрационных коэффициентов на n-ом шаге итерационного процесса, 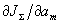 - проекции градиента функционала JΣ относительно функций - проекции градиента функционала JΣ относительно функций 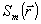 , которые, как не сложно показать, анализируя изменение ΔJΣ, вызванное малым изменением Δаm, определяются выражением: , которые, как не сложно показать, анализируя изменение ΔJΣ, вызванное малым изменением Δаm, определяются выражением:
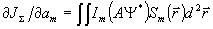 . .
На рис.3 приведена динамика изменения критерия JΣ в процессе итераций для аберраций различной силы. Определение коэффициентов
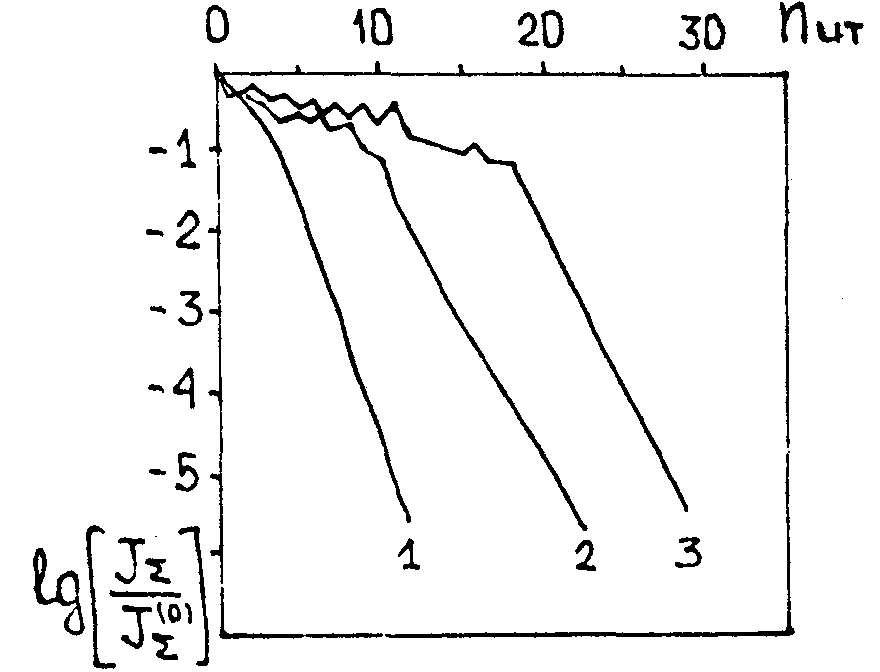
Рис.3. Динамика сходимости итерационного процесса определения аберрационных коэффициентов волнового фронта по набору изображений L={0,1, ∞):
1 – a=0,1 λ, 2 – a=0,20λ, 3 – a=0,25λ.
а m производилось по набору из двух изображений (L={0.1, ∞}). Заметим, что теперь изменение критерия JΣ (особенно в начале итерационного процесса) происходит немонотонным образом, что не наблюдалось при восстановлении всей фазы (см.рис.1).
Следует отметить также, что предлагаемый метод анализа волнового фронта имеет примерно в M/2 раз меньше вычислительные затраты на один итерационный шаг и в 5 раз больший диапазон восстановления, чем итерационный алгоритм, предложенный в /10,11/.
Все приведенные в работе результаты по восстановлению фазы и определению аберрационных коэффициентов волнового фронта получены при одной и той же начальной оценке фазы 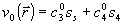 . Коэффициенты . Коэффициенты 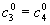 полагались равными 0,01λ (максимальный размах такой фазы по апертуре равен 0,06λ, т.е. она слабо отличается от плоского волнового фронта). полагались равными 0,01λ (максимальный размах такой фазы по апертуре равен 0,06λ, т.е. она слабо отличается от плоского волнового фронта).
Таким образом, предлагаемый метод позволяет с единых позиций подойти к решению задачи восстановления фазы световой волны по ряду зарегистрированных распределений интенсивности и дает возможность синтеза эффективных алгоритмов восстановления, которые могут лечь в основу экспресс-методов анализа волнового фронта.
Л и т е р а т у р а
1. Аблеков В.К., Колядин С.А., Фролов А.В. Высокоразрешающие оптические системы. М., Машиностроение, 1985, с.176.
2. Обратные задачи в оптике (под ред.Болтса Г.П.) М., Машиностроение, 1984, с.200.
3. Аблеков В.К. и др. Доклады АН СССР, т.261, №3, 1981, с.609-610.
4. Васильев Ф.П. Методы решения экстремальных задач. Наука, М., 1981, с.400.
5. Gerchberg R.W., Saxton W.O. - Optik, 1972, v.35, 2, 237-246.
6. Fienup J.R. - Appl.Opt., 1982, v.21, 15, 2758-2769.
7. Аблеков В.К. и др. Доклады АН СССР, т.271б №6, 1983, с.1377-1379.
8. Клибанов М.В., Волостников В.Г., Котляр В.В. Доклады АН СССР. т.279, №6, 1984, с.1348-1351.
9. Клибанов М.В. Доклады AН СССР, т.285, №2, 1985, с.278-260.
10. Саутвэл В. //Адаптивная оптика., под ред.Витриченко Э.А., Мир, М., 1980, с.416-427.
11. Nahrstedt D.A., Southwell W.H. - Appl.Opt., 1984, v.23, 23, 4328-4331.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

