|
|
 |
 |

|
| |
АЛГОРИТМ, ВОССТАНАВЛИВАЮЩИЙ КОМПЛЕКСНОЕ
СВЕТОВОЕ ПОЛЕ ПО ДВУМ РАСПРЕДЕЛЕНИЯМ ИНТЕНСИВНОСТИ
И НЕКОТОРЫЕ ВОЗМОЖНЫЕ ЕГО ПРИМЕНЕНИЯ
Т.И.Кузнецова
За последние 15 лет в литературе по оптике сформировалось новое направление, относящееся к обработке информации, передаваемой световыми полями. Было выявлено, что применение надлежащих математических методов при обработке оптических изображений дает удобный способ восстановления волновых фронтов световых полей, а также позволяет синтезировать оптические элементы, заданным образом воздействующие на световые поля. Начало этому направлению положила работа /1/.
Разумеется, проблема извлечения фазовой информации из данных об интенсивности поля привлекала внимание исследователей задолго до появления /1/. Однако в более ранних работах речь шла об использовании данных об интенсивности, относящихся только к одной плоскости. Такой подход изложен, например, в /2-4/. В этих работах можно найти соотношения, связывающие пространственное распределение фазы поля с распределением интенсивности. Эти соотношения содержат, кроме пространственного распределения интенсивности, еще ряд величин, которые обычно не удается извлечь из измерений простым способом. К настоящему времени выяснено (см. /5/), что абстрактная возможность получить фазовые характеристики поля, переносящего изображение, по амплитудным - имеется, и на определенном классе функций можно обеспечить единственное решение. Однако, реально построить такое решение никогда не удается. Причина этого в том, что задача восстановления фазы по амплитуде является некорректно поставленной: малым отличиям в распределении амплитуды могут соответствовать сильные отличия в распределении фазы. Поэтому реально зарегистрированная интенсив-
ность, содержащая шумы, не дает возможности восстановить правильное фазовое распределение.
Основа успеха, достигнутого в работе /1/, заключается в том, что авторы ее ввели в рассмотрение больше входной информации, чем это необходимо для единственности решения задачи: они стали использовать распределения интенсивности в двух плоскостях (а не в одной), чем обеспечили регуляризацию фазовой задачи. Следует сказать, что идеи регуляризации в строгой формулировке проникли в оптику несколько позже, чем была выполнена работа /1/ (см. /6/ и указанную здесь литературу), сама же работа содержала просто описание удачно найденного алгоритма. Ниже мы даем изложение работы /1/.
Алгоритм Гершберга-Сэкстона
Допустим, что исходное монохроматическое поле, несущее информацию о заданном объекте, было зарегистрировано в двух плоскостях: в плоскости изображения и в Фурье-плоскости. Обозначим поле в плоскости изображения через Е(х)=а(х)ехр(iφ(x)), в Фурье-плоскости - через F(x')=А(x')ехр(iФ(x')), для операции преобразования Фурье введем символ L, так что
F(x')=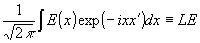 . .
При регистрации получена информация о функциях а(х) и А(х'), а информация о фазовых множителях потеряна. Задача состоит в построении комплексной функции по заданному ее модулю и модулю ее Фурье-образа. Для решения этой задачи Гершберг и Сэкстон предложили итерационную процедуру, которая заключалась в следующем. В качестве пробной функции бралась функция, модуль которой совпадал с заданным в плоскости изображения модулем а(х), а фазовый множитель ехр( iΨ(x)) брался произвольный, в работе он строился с помощью генератора случайных чисел. Эту функцию удобно обозначить через у0(х), где индекс соответствует числу итераций, у0(х)=а(х)ехр(iΨ(x)). Для этой функции строилось преобразование Фурье Lу0=А0( х)eхр(iФ0(x )). Затем у полученной функции модуль заменялся на правильный, т.е.
на А (х), а фаза сохранялась, Так получали функцию в Фурье-плоскости Y0(х)=A(х)exp(iФ0(х)), что можно представить как
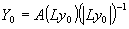 . .
Затем выполнялось обратное преобразование Фурье и снова исправлялся модуль, при этом получалась функция в плоскости изображения в первом приближении
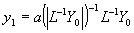 . .
На следующем шаге выполнялись такие же преобразования. Всю итерационную процедуру можно представить формулами :
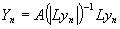 , , 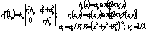 . (1) . (1)
Если процесс окажется сходящимся, то функцию, получающуюся в качестве предела итераций, будем обозначать через у,
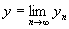 . .
Во многих случаях процесс действительно сходился, и функция у совпадала с исходным комплексным полем a exp(iφ). Однако, ни существование решения, ни его единственность здесь не гарантируются. Тем не менее, многочисленные удачи в численном эксперименте привели к тому, что алгоритм стали широко использовать другие авторы. Более того, алгоритм Гершберга-Сэкстона стали применять к несколько иным задачам, возникли его модификации, обусловленные как измененной постановкой задачи, так и стремлением ускорить численную процедуру. Здесь прежде всего следует упомянуть задачу восстановления неотрицательной функции по заданному модулю ее Фурье-спектра /7/ и задачу для двумерных нефакторизуемых функций /8/.
Схема оптического устройства для восстановления
фазовых характеристик световых полей
Поставим вопрос, нельзя ли процедуру, описанную в п.2, выполнить с помощью оптических преобразований. Пусть информация о функциях а(х) и А(х), введенных выше, представлена в виде пропускания транспарантов. Потребуем, чтобы при помещении транспарантов в специальную оптическую систему на выходе системы формировалась волна, имеющая правильную пространственную зависимость как амплитуды, так и фазы. Рассмотрим однонаправленный кольцевой лазер (рис.1). Линза 4 осуществляет фурье-преобразова-
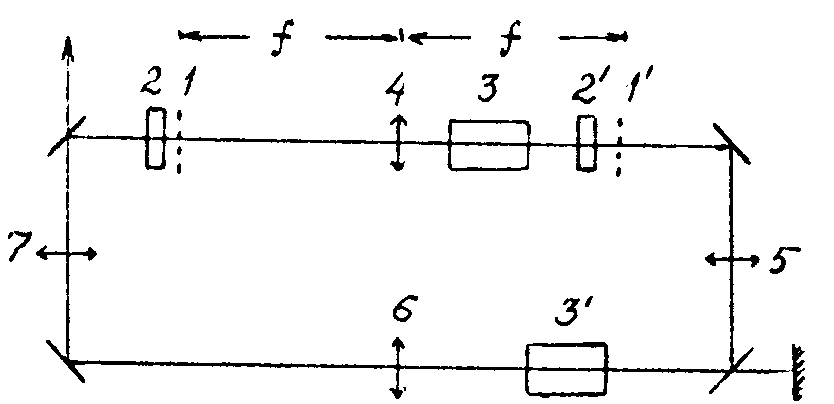
Рис.1. Однонаправленный кольцевой лазер.
ние от плоскости 1 к 1 ', линзы 5-7 дают обратное преобразование Фурье от 1' к 1. Все линзы имеют фокусные расстояния, равные f, длина оптического пути при полном обходе резонатора составляет Sf. В плоскостях 1 и 1' должны быть помещены транспаранты. Усиливающие элементы 3 и 3' (каждый с коэффициентом усиления β) предназначаются для компенсации потерь на транспарантах. Каждый усиливающий элемент должен быть достаточно однородным и иметь достаточную угловую апертуру (см.требования, предъявляемые к усилителям яркости для оптических приборов, в /9/). Перед каждым транспарантом следует поместить нелинейно поглощающий элемент, который будет сглаживать поперечную структуру интенсивности световой волны, оставляя фазовое распределение неизменным (элементы 2 и 2' на рис.1). Если, например, нелинейность обес-
печивается двухфотонным поглощением и толщина поглотителя l мала по сравнению с дифракционной длиной, то можно воспользоваться уравнением
 (2) (2)
и получить, что поле у(х), падающее на поглотитель, на выходе из поглотителя перейдет в N(у(x)), где
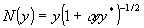 . (3) . (3)
Ясно, что преобразование (3) дает частичное выравнивание интенсивности. Схема устройства и анализ его работы содержатся в /10,11/.
Если бы такое устройство было реализовано, его действие являлось бы альтернативой голографическому способу регистрации и воспроизведения световых полей. При этом процесс регистрации поля, который здесь требуется, оказывается гораздо проще, чем традиционный голографический.
Алгоритм для восстановления фазовых характеристик,
моделирующий действие оптического устройства
В оптическом устройстве, описанном в п.4, выполняются нелинейные преобразования поля в поглотителе, умножение на транспаранты, преобразование Фурье, усиление. Поля на последовательных проходах, уn и уn+1, связаны друг с другом уравнением
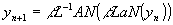 . (4) . (4)
Входящие в (4) операторы N, L, а также величины а, А, β определены в п.п.2,3. Следует обратить внимание, что при сильных нелинейностях (|y|2→∞) алгоритм (4) переходит в алгоритм (1). По формуле (4) в /10,11/ проводились численные расчеты. При расчетах мы брали оператор N в виде (3), причем для простоты полагали в (3) α=1. Значение α можно брать
любое, поскольку изменение α эквивалентно перенормировке интенсивности поля |у|2. Можно было бы вместо (3) ввести нелинейность другого вида. например, связанную с генерацией ВКР, с насыщением усиления; важно только, чтобы нелинейное преобразование сглаживало выбросы интенсивности.
Если начинать расчеты с малых интенсивностей, |y0|<<1, то, в зависимости от параметра β, можно прийти к одному из двух режимов. При малых β поле затухает от прохода к проходу, в течение всех итераций нелинейность на поле не действует. При этом за 8-10 итераций достигается устойчивое распределение по координате х, а среднее значение от итерации к итерации затухает (допороговый режим). В этом режиме установившееся распределение у(х) и исходное поле а(х)ехр(iφ(x)) имеют интеграл перекрытия ≈0,75÷0,90.
При больших β (надпороговый режим) поле сначала растет, затем, после нескольких итераций, включается нелинейность, рост замедляется и, наконец, устанавливается стационарное среднее значение интенсивности и устойчивое распределение поля по x. При этом можно получить более высокое значение интеграла перекрытия функций у(x) и a(x)ехр(iφ(x)), чем в допороговом режиме. Обычно - без сколько-нибудь тщательного подбора значений β и |y0| - легко достигались значения интеграла перекрытия ≈ 1 - 3∙10-3, они устанавливались за 15÷20 итераций. Однако в сильно нелинейном надпороговом режиме возможны случаи выхода на неправильное решение (с интегралом перекрытия <0,5); частота их появления растет с увеличением β. Чтобы избежать их, следует уменьшать начальную интенсивность, тем самым затягивая линейную стадию итераций.
Связь с задачами построения киноформов
Как известно, при синтезе киноформа решается задача подбора фазовой функции по двум распределениям интенсивности: равномерное распределение в плоскости транспаранта (обычно кусочно-постоянное, иногда - Гауссово) и заданная сложная пространственная картина в дальней зоне. Нормально здесь мы имеем те же исходные данные, как в задаче восстановления фазы поля, интенсивность которого зарегистрирована в двух плоскостях. Поэтому
при построении киноформов пользуются алгоритмами типа Гершберта-Сэкстона. Литературу по этому вопросу можно найти в /12/. Есть, впрочем, и другой подход к расчету киноформов (см.,например, /13/).
Есть однако важнее отличие фазовой задачи от задачи синтеза киноформа. В случае восстановления фазы всегда известно, что решение существует. Действительно, в фазовой задаче мы имеем два распределения интенсивности, полученные для объектного поля, которое реально существовало; эти два распределения можно назвать согласованной парой. В случае киноформа заранее не ясно, существует ли такое комплексное поле, которое содержит оба заданных распределения интенсивности.
Численные расчеты по киноформам показали, что если требуется заданное для дальней зоны пространственное распределение воспроизвести с грубой точностью, то решение обычно удается построить. Однако задача повышения точности, как правило, оказывается невыполнимой (заданные входное и выходное распределения не являются согласованной парой). Эта ситуация описана в /12/.
В /12/ предложен такой путь улучшения характеристик киноформов: высокая точность в центральной области выходного распределения интенсивности достигается за счет того, что допускается некоторый произвол в периферийной области.
Связь с задачами измерения
временных характеристик лазерного излучения
В настоящее время ведутся многочисленные работы по исследованию временной структуры лазерного излучения как прямыми, так и некоторыми косвенными методами. Последние достижения в этой области изложены, например, в /14/. Не исключено, что при изучении временных характеристик света может найти применение алгоритм Гершберга-Сэкстона и его модификации.
В частности, с помощью алгоритмов можно было бы проводить исследование фазовой модуляции световых импульсов на основе данных о временном ходе интенсивности и о спектре. Разумеется, при этом необходимо высокое разрешение как временное, так и спектральное.
Новая возможность возникает также при изучении временного хода интенсивности излучения на основе данных о корреляционной функции интенсивности. Легко показать, что здесь задача сводится к задаче восстановления неотрицательной функции по модулю ее Фурье-спектра. Для решения этой задачи известен алгоритм /7/. К сожалению, требования к точности измерения корреляционной функции, сформулированные в /15/ в новом подходе не снимаются.
Литература
1. Gerchberg R.W., Saxton W.O. 1971, 35, 237-246.
2. Мандель Л., Вольф Э. УФН (1966), 88, 619-673.
3. Нуссенцвайг Х.М. Причинность и дисперсионные соотношения. М., "Мир". 1976.
4. Клаудер Дж., Сударшан Э. Основы квантовой оптики. М., "Мир", 1970.
5. Ферверда Х.А. Проблема восстановления фазы волнового фронта по амплитудному распределению и функциям когерентности. Обратные задачи в оптике, ред. Г.П.Болтс, М., Машиностроение, 1984.
6. Bertеro M., DeMol C., Viano G.A., The Stabillty оf Inverce Problems. In:Inverse Scattering Problems in Optics Ed.H.P.Baltes, N.-Y., 1980.
7. Fienup J.R. Appl.Optics, 1982, 21, 2758-2769.
8. Bates R.H.T., Tan D.G.H. JOSA. s еr.A, 1985, 2, 2013-2017.
9. Петраш Г.Г. Вестник АН СССР (1962), 2, 66-75.
10. Кузнецова Т.Н., Кузнецов Д.С. Квантовая электроника (1965), 12, 2507-2509.
11. Кузнецова Т.И., Кузнецов Д.Ю. Краткие сообщения по физике, ФИАН. 1986, №2, с.12-14.
12. Hiroshi Аkanori. Аррl.Орtics, 1986, 25, 802-811.
13. Гончарский А.В., Данилов В.А., Попов В.В., Прохоров А.М., Сисакян И.Н., Сойфер З.А.. Степанов В.В. ДАН СССР (1983), 273, 605-608.
14. Щелев М.Я. Тр.ФИАН. Пикосекундная электронно-оптическая диагностика в лазерных исследованиях" (1985), 155, с.3-145,
15. Кузнецова Т.Н. ЖЭТФ (1968), 55, 2453-2458.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

