|
|
 |
 |

|
| |
ГОЛОГРАФИЯ ВОЛНОВЫХ ПАКЕТОВ
Ю.Т.Мазуренко
Рассмотрены методы регистрации, восстановления и преобразования пространственно-временных оптических сигналов, основанные на интерференции, дифракции и нелинейных взаимодействиях сверхкоротких импульсов, подвергнутых пространственному спектральному разложению.
1. В настоящее время возможно получение сверхкоротких оптических импульсов, длительность которых достигает 10 -14 с и менее. Волновые пакеты, сформированные из таких импульсов, имеют продольные размеры, существенно меньшие, чем характерные размеры элементов оптических систем. Это позволяет реализовать условия, при которых дифракция волнового пакета на пространственных неоднородностях приводит к изменению не только пространственной, но и временной структуры излучения. Если распределение неоднородностей в пространстве надлежащим образом соответствует распределению в пространстве и времени амплитуды и фазы некоторой нестационарной волны, то (в рамках определенных ограничений) возможно восстановление этой волны при дифракции на пространственных неоднородностях короткого волнового пакета. Это обстоятельство позволяет осуществить непосредственную регистрацию в трехмерной среде и последующее восстановление ограниченной во времени нестационарной волны при использовании в качестве опорного излучения плоского короткого волнового пакета
Более широкие возможности возникают при использовании пространственного спектрального разложения сверхкоротких импульсов.
Любой временной сигнал, как известно, может быть определен через его комплексный спектр (фурье-образ), содержащий в общем
случае амплитудную и фазовую структуру. При реальном Фурье-анализе частотное разрешение аппаратуры, с помощью которого формируется спектр временного сигнала, должно удовлетворять условию Δ ν<<1/τ γде τ - размер наиболее грубой временной структуры сигнала, например, его длительность. Спектральное разложение в оптике основано на многолучевой интерференции, поэтому величина спектрального разрешения определяется в конечном счете максимальной пространственной задержкой, т.е. максимальной разностью хода, интерферирующих лучей, которая достигается в данном приборе. Если максимальная разность хода равна L, то частотное разрешение прибора составляет Δν≈ρ/L и в лучших случаях может достигать 108-10 9 Гц. Таким образом, условие Δν<<1/τ означает, что размер волнового пакета, подвергаемого спектральному разложению, должен быть существенно меньше реализуемых значений разности хода L, что практически возможно только для сверхкоротких оптических импульсов.
Несмотря на это обстоятельство, ряд важных результатов по свойствам сверхкоротких импульсов был получен задолго до их реального появления. Эти результаты были получены при исследовании волновых свойств белого света. Фактически первые опыты, демонстрирующие фазовую структуру оптического спектра, поставили Фуко и Физо, которые наблюдали полосы двухлучевой интерференции в спектре белого света - канавчатый спектр /2/. Рэлей и Устер объясняли эти опыты как результат интерференции очень коротких (~10 -14 с) импульсов, составляющих белый свет /3/. Интерференция сверхкоротких импульсов белого света рассматривалась также в связи с объяснением полос Тальбота /3/.
Появление изолированных сверхкоротких световых импульсов возродило интерес к интерференции спектрально разложенного света. Так, в работах /4,5/ было предложено использовать интерференцию спектров двух импульсов для регистрации формы одного из них. Было рассмотрено действие дифракции на временную форму сверхкоротких импульсов /5,6,7/. В работах /8,9/ были предложены методы голографической регистрации и восстановления зависящих от времена оптических сигналов при использовании вращающейся опорной волны.
Следует также отметить возможности спектральной регистрации и восстановления сверхкоротких импульсов с помощью светочувствительных сред, обладающих малым однородным и большим неоднородным уширением спектра поглощения света /10/.
В настоящей работе рассмотрены методы регистрации, восстановления и преобразования пространственно-временных оптических сигналов, основанные на интерференции, дифракции и нелинейных взаимодействиях сверхкоротких импульсов /11-17/.
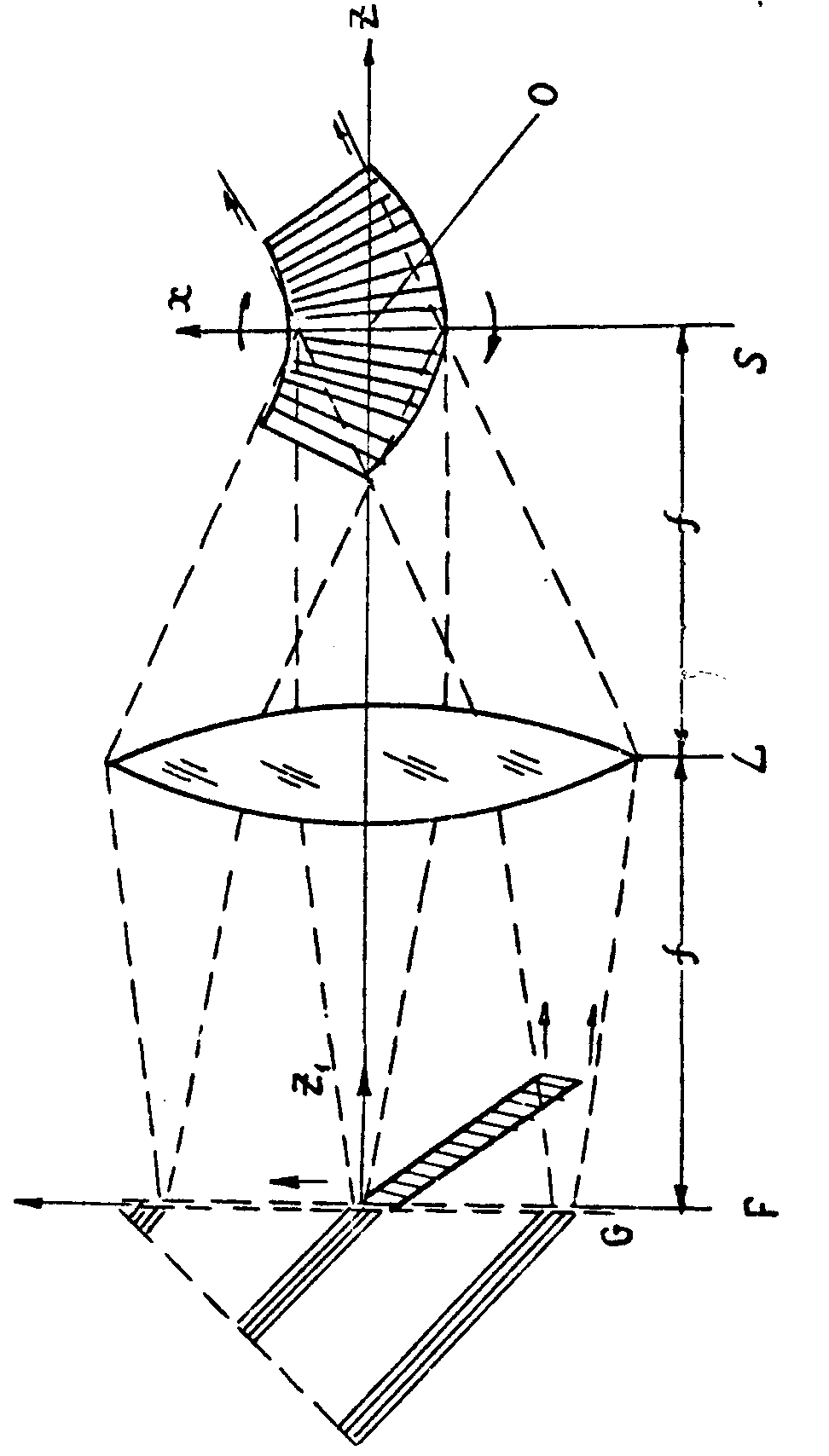
2. Рассмотрим волновые поля, формируемые при пространственном спектральном разложении сверхкоротких световых импульсов. На рис.1 изображена схема спектрального прибора, состоящего из диспергирующего элемента G (в данном примере дифракционной решетки, работающей на пропускание) и объектива L. Диспергирующий элемент расположен вблизи передней фокальной плоскости объектива F. Плоскость спектра S совпадает с задней фокальной плоскостью объектива. Действие диспергирующего элемента можно рассматривать как прохождение плоских волн через эквивалентный транспарант, обладающий комплексным пропусканием:
G(Ω,x)=p(x)exp(iβΩx/c).
В этом выражении x - поперечная координата в плоскости F, параллельная направлению спектрального разложения, Ω=ω-ω0, ω - частота света, ω0 - частота света, распространяющегося а направлении оптической оси прибора, р(x) - функция, описывающая апертурные ограничения, β - характеристика угловой дисперсии, с - скорость света /12//
Пусть на диспергирующий элемент G падает плоский волновой пакет, временной профиль которого описывается выражением r(t)exp(-ω0t), где r(t) - комплексная огибающая. Введем спектр комплексной огибающей:
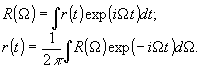 (1) (1)
Рассматривая в спектральном представлении фильтрацию этого излучения транспарантом G(Ω,x), а затем переходя от спектрального представления к временному с помощью (1), получим следующее распределение поля на передней фокальной плоскости объектива L после прохождения излучением диспергирующего элемента:
v(t,x)=r(t-βx/c)p(x)exp(-iω 0t). (2)
Распределение (2) можно наглядно интерпретировать как поле, создаваемое источником монохроматического излучения, который обладает распределением амплитуды по координате x, повторяющим временную форму импульса r(t), и двигается по плоскости F со скоростью с/β (см.рис.1). Поскольку не существует принципиальных ограничений величины β, скорость движения этого источника может быть как меньше, так и больше скорости света. Если размер апертуры диспергирующего элемента (определяемый функцией р(x)) равен а, то время пробега рассматриваемого источника по апертуре равно Т=aβ/c. Это время может быть названо временем отклика спектрального прибора, определяющим его частотное разрешение Δω=2π/Т. Будем считать в дальнейшем, что длительность импульса τ<<T. Это соответствует рассмотренным выше условиям формирования его полного спектра.
Найдем также распределение поля в пространстве, примыкающем к плоскости F и ограниченном ближней зоной дифракции. Нетрудно показать, что область ближней зоны дифракции определяется выражением
z01 =2πω0c/(βΩ0) 2,
где Ω0 - ширина спектра импульса r(t). Если z1 - продольная координате, отсчитываемая от плоскости F, то при условии |z1|<z01 пространственное распределение поля имеет вид:
v(t,x,z1 )=r[t-(βx-z1)/c]exp[i(k 0z 1-ω0t)]. (3)
Выражение (3) описывает монохроматический луч, перемещающийся в поперечном направлении. Благодаря высокой скорости поперечного перемещения луч наклонен по отношению к направлению его волнового вектора.
Рассмотрим теперь волновое поле спектрального разложения импульса, формируемое вблизи плоскости S. Качественно структуру этого поля можно представить себе следующим образом. Излучение бегущего по плоскости F небольшого источника монохроматического излучения преобразуется объективом L в параллельный пучок лучей, вращающийся вокруг заднего фокуса О. Несмотря на вращение пучка скорость распространения волн должна быть постоянной и равной скорости света в любой точке его поперечного сечения. Это возможно лишь в том случае, если пучок искривлен как показано на рисунке. Длина волны в искривленном пучки зависит от координаты в его поперечном сечении, что и означает реализацию спектрального разложения импульса (см.рис.1).
Строгое рассмотрение нетрудно провести, пользуясь методами фурье-оптики. Используя фурье-преобразующие свойства объектива L и учитывая условие τ<<Т, получим следующее пространственное распределение поля вблизи плоскости S, создаваемое при спектральном разложении импульса z(t) /13-17/
u(t,x,z)=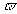 (t)R(αx)exp[i(ω0+αx)(z/c-t)]. (4)
Здесь z - координата, отсчитываемая в направлении оптической оси от плоскости S, α=dΩ/dx - линейная дисперсия на плоскости спектра, 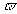 (t)=const∙p(ct/β) - функция временного отклика спектрального прибора (ее длительность равна Т). Выражение (4) справедливо в пределах ближней зоны дифракции относительно плоскости спектра. Глубина ближней зоны равна (t)=const∙p(ct/β) - функция временного отклика спектрального прибора (ее длительность равна Т). Выражение (4) справедливо в пределах ближней зоны дифракции относительно плоскости спектра. Глубина ближней зоны равна
z02 =(f/ω2λ0, где λ0 - длина волны, отвечающая Ω0.
Поверхность постоянной фазы волны (4) расположена веерообразно, поэтому волна спектрального разложения (4) может быть кратко названа веерной волной. Нетрудно видеть, что эта волна содержит полный набор разделенных в пространстве амплитудных частотных составляющих исходного волнового пакета и поэтому является реализацией амплитудного спектрального разложения в оптике.
Волновой пакет, падающий на вход спектрального прибора, кроме временной модуляции может также содержать и пространственную модуляцию в направлении оси у, перпендикулярной направлению спектрального разложения. С учетом этого обстоятельства огибающая волнового пакета может быть записана в виде r(t,y), где у - координата на передней фокальной плоскости объектива. Распределение r(t,y) фактически описывает некоторое нестационарное одномерное изображение. Преобразование падающего излучения спектральным прибором рис.1. при малой апертуре происходит по координатам х и у независимо. При этом в сечении у спектральный прибор работает как обычное устройство оптического Фурье-преобразования изображения, формирующее на плоскости S спектр пространственных частот. Спектр пространственных частот S(ky) изображения S(у) запишем в виде:
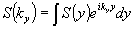 ; ; 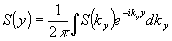 , (5) , (5)
где kу - проекция волнового вектора на ось у (пространственная частота). Исходя из (1), (5), нестационарному изображению r(t,у) может быть сопоставлен двумерный спектр пространственно-временных частот R(Ω, kу):
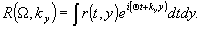 (6) (6)
Амплитудный двумерный спектр R(Ω,ky) изображается объективом L на плоскости S в виде распределения амплитуды поля R(αx,γу), где α и γ - коэффициенты подобия между временной и пространственной частотой и координатами на плоскости S. При учете поперечной пространственной модуляции волнового пакета распределение R(αх) в (4) следует заменить на R(αυ, γу) в соответствии с (6).
3. Пусть на диспергирующий элемент спектрального прибора G (рис.2) падают два коротких волновых пакета a и b. Если расстояние между ними в шкале времени меньше, чем Т, то возможна интерференция волн их спектральных разложений. Найдем картину интерференции на плоскости спектра S. С целью последовательного проведения аналогий с фурье-голографией эту задачу полезно рассмотреть с помощью представления о бегущих излучателях, описываемых выражением (2).
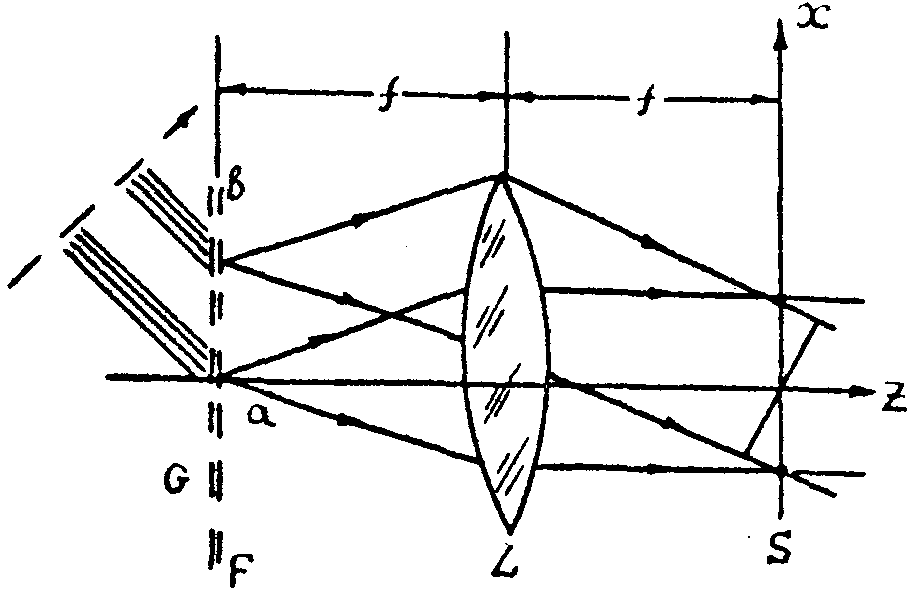
Рис.2. Регистрация двумерной спектральной голограммы.
В рассматриваемом случае существует два бегущих излучателя a и b, движущихся с одинаковой скоростью. Хорошо известно, что картина интерференции, создаваемая на задней фокальной плоскости линзы источниками, расположенным на ее передней фокальной
плоскости, практически не изменяется, если источники перемещать синхронно. Поэтому интересующая нас картина интерференции не отличается от картины интерференции двух неподвижных излучателей, соответствующих двум падающим на диспергирующий элемент волновым пакетам. В частном случае точечных излучателей, соответствующих двум "мгновенным" импульсам, картина интерференции имеет вид периодически расположенных полос. В частотной шкале расстояние между полосами равно Δ ω1=2π/Δt, где Δt - расстояние между импульсами во временной шкале. Из этого рассмотрения вытекает, что существует весьма близкая аналогия интерференции временных и пространственных частот в оптике.
Развивая эту аналогию в количественном отношении либо пользуясь полученными выше выражениями для волн спектрального разложения, найдем, что распределение интенсивностей на плоскости спектра с учетом поперечной пространственной модуляции двух волновых пакетов имеет вид :
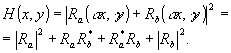 (7) (7)
Здесь Ra(Ω,ky), R b(Ω,ky) -пространственно-временные спектры волновых пакетов ra(t,y), rb(t,y). Распределение (7) можно назвать двумерной спектральной голограммой. Эта голограмма содержит регистрацию пространственно-временной формы сигнального излучения, например, ra(t,y), относительно опорного излучения rb(t,y). В качестве опорного излучения можно выбрать "мгновенный" импульс, ограниченный на плоскости F узкой целью вблизи у=0. Такому импульсу отвечает спектр Rb(Ω, kу)~const=В. При этом (7) преобразуется к виду:
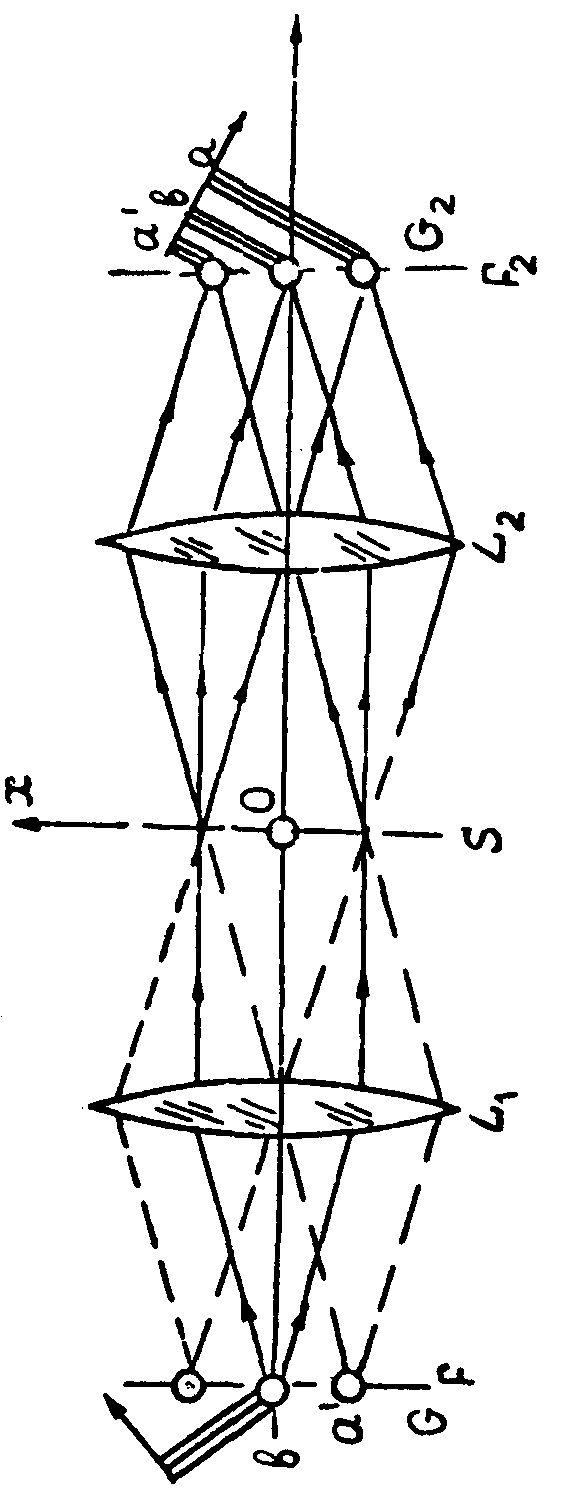
H(x,y)=|Ra|2+(Ra+Ra*)B+B2. (8)
4. Перейдем к восстановлению волнового пакета, записанного на спектральной голограмме /11-14/. Для этого воспользуемся двойным спектральным прибором, изображенным на рис.3. Левая ветвь схемы рис.3 аналогична схемам рис.1 и 2, а правая ветвь является зеркальным отражением левой от плоскости спектра S. Поскольку элементы G1 и G2 взаимно компенсируют свою дисперсию, то при отсутствии преград в плоскости S прибор не изменяет формы прошедшего сквозь него короткого волнового пакета. Поместим в плоскость S прибора проявленную спектральную голограмму (7) и (8) и направим на G1 копию опорного волнового пакета (восстанавливающее излучение). Вновь обращаясь к аналогии с фурье-голографией, рассмотрим в сечении xoz схемы результат дифракции на голограмме излучения, исходящего от бегущего по плоскости G1 излучателя, который создан опорным волновым пакетом. Рассмотрим простейший случай спектральной голограммы двух мгновенных импульсов, не содержащих поперечной модуляции. Такая голограмма, как отмечалось, фактически является периодической решеткой. Предположим вначале, что точечный излучатель, создаваемый восстанавливающим волновым пакетом на плоскости G1, неподвижен. В этом случае на голограмму падает параллельный пучок лучей. При дифракции параллельного пучка на решетке возникают, как обычно, два новых параллельных пучка, отклоненные в обе стороны от падающего на одинаковый малый угол. Этим пучкам на плоскости G1 соответствуют точечные мнимые изображения а и а', расположенные по обе стороны от излучателя b. Пусть теперь источник b перемещается по плоскости F1 вместе с восстанавливающим волновым пакетом. В этом случае падающий на плоскость S-пучок и оба дифрагированных пучка синхронно вращаются, а мнимые восстановленные изображения а и а' перемещаются по плоскости F, синхронно с излучателем b. При этом одно из восстановленных изображений не отличается от бегущего изображе-
ния , создаваемого сигнальным волновым пакетом при записи голограммы, а другое соответствует сигнальному волновому пакету, обращенному во времени. Иными словами, наблюдая излучение справа от плоскости S невозможно отличить дифрагированные на спектральной голограмме волны от волн спектрального разложения сигнального импульса и импульса, который является его обращением во времени (обращение во времени происходит относительно момента появления опорного импульса). После прохождения дифрагированных на голограмме волн сквозь правую ветвь спектрального прибора рис.3 формируется реальная временная копия сигнального волнового пакета и его копия, обращенная во времени. Эти выводы нетрудно распространить на импульсы произвольной формы.
Восстановление можно рассматривать и как результат фильтрации волн спектрального разложения голограммой (7) или (8). В частности, при восстановлении двумерной голограммы (8) мгновенным точечным импульсом получим две представляющие интерес волны, сформированные вблизи плоскости спектра S.
[Ra (αx,γy)+Ra*(αx,γy)]exp[i(ω0+αz)(z/c-t)].
Первая волна ничем не отличается от волны спектрального разложения сигнального волнового пакета ra(t, у), вторая - отвечает сигналу rа*(-t, -у), т.е. сигнальному излучению, обращенному во времени к пространстве. Если при записи голограммы опорный и сигнальный импульсы пространственно разделены в сечении уoz - схемы, то при восстановлении оказываются пространственно разделенными восстанавливающий импульс, прямая и обращенная во времени копии сигнального импульса, а также сигнал корреляции сигнального импульса, отвечающий компоненте |Ra|2 голограммы (8).
Учет конечной величины спектрального разрешения приводит к ограничению длительности регистрируемого и восстанавливаемого сигнального импульса величиной ~ Т = 2π /Δω. Временное разрешение регистрации и восстановления определяется обратной величиной ширины спектра опорного импульса (если этот спектр до-
статочно равномерен).
В работе /12/ рассмотрены также регистрация и восстановление двумерных нестационарных изображений, основанные на использовании методов многолучевой интерферометрии и голографии. В этом случае запись движения объекта на фурье-голограмме обеспечивается в результате дискретизации регистрируемого спектра пространственных частот объекта, позволяющей освободить место для регистрации спектра временных частот.
5. Естественным развитием аналогии обычной и спектральной голограммы является объемная спектральная голограмма - аналог голограммы Ю.Н.Денисюка /16/. Регистрация и восстановление такой голограммы показаны на рис.4. Опорный и сигнальный импульсы падают на разные диспергирующие элементы двойного спектрального прибора и распространяются один навстречу другому. Соответствующие им встречные волны спектрального разложения при надлежащем временном согласовании могут интерферировать в течение времени ~Т в слое, окружающем плоскость спектра S и имеющем толщину, равную дифракционной глубине резкости 2Z02. Объемная картина интерференции имеет вид стоячей веерной волны:
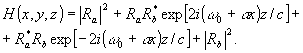 (9) (9)
Запись картины интерференции (9) в объемной регистрирующей среде приводит к получению объемной спектральной голограммы. Объемная спектральная голограмма (9) содержит в направлении оси z слоистую структуру с периодом, равным, как обычно, половине длины волны зарегистрированного излучения. Однако, поскольку в данном случае длина волны интерферирующих излучений зависит от координаты х, то слои структуры расположены веерообразно. Существование продольной периодической структуры приводит к отражательной способности объемной спектральной голограм-
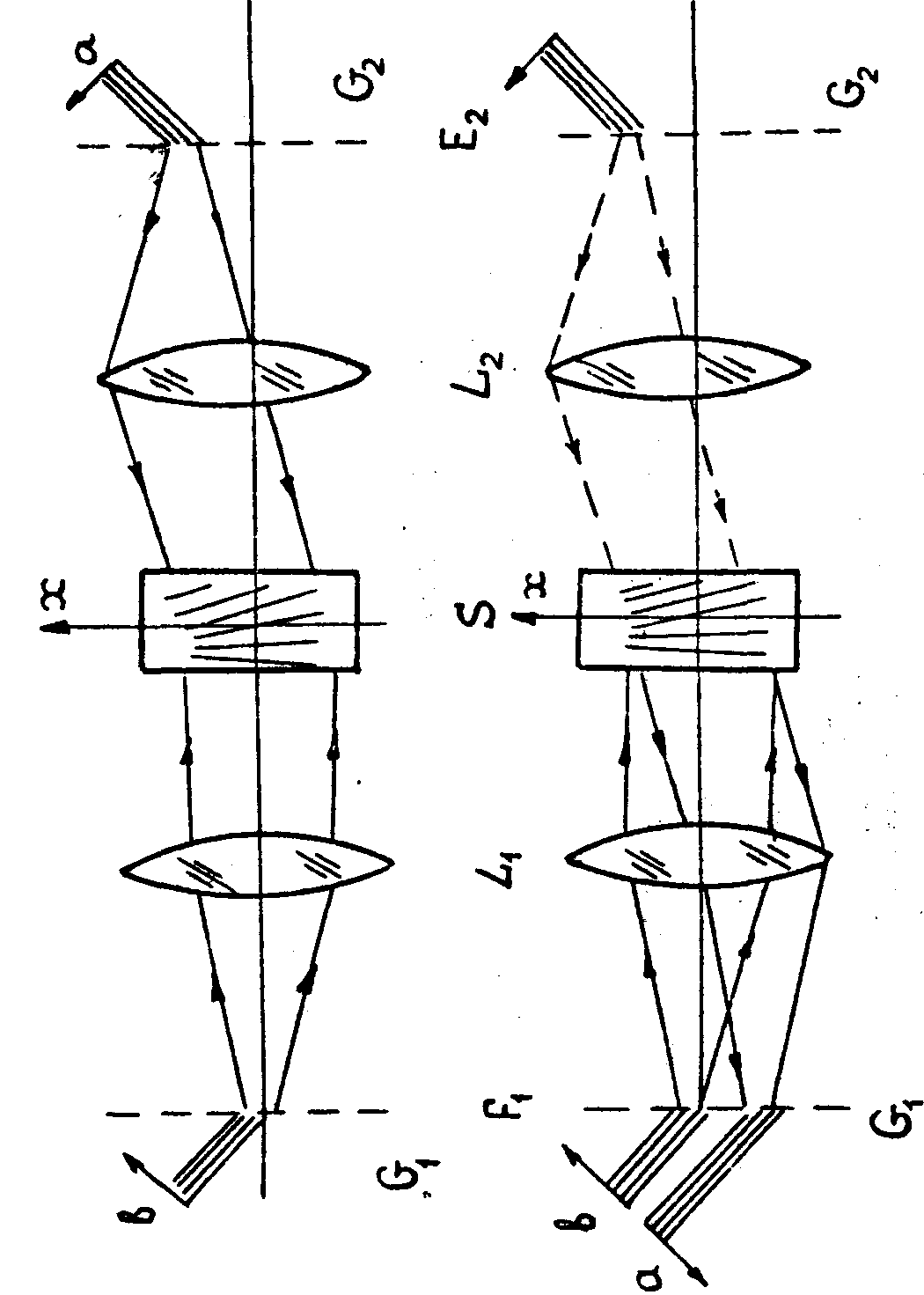
мы, поэтому ее восстановление должно осуществляться в отраженном свете. Направляя в спектральный прибор копию опорного волнового пакета, получим при отражении волны его спектрального разложения от голограммы и прохождения сквозь диспергирующий элемент копию сигнального волнового пакета, свободную от побочных излучений (рис.4). Чтобы получить обращенную во времени копию сигнального излучения следует освещать объемную спектральную голограмму при восстановлении со стороны, противоположной той, с которой она освещалась при записи.
Таким образом, при использовании объемной спектральной голограммы не возникает проблемы пространственного разделения восстановленного сигнального излучения и его копии, обращенной во времени, а также отделения восстановленного излучения от восстанавливающего и от автокорреляционного сигнала. Кроме того, как известно, объемные голограммы принципиально обладают высокой эффективностью восстановления, что естественным образом переносится и на спектральные голограммы.
6. Из изложенного выше видно, что когерентные преобразования коротких временных сигналов при дифракции волн их спектральных разложений имеют весьма близкую аналогию с когерентными преобразованиями пространственных сигналов (изображений) в фурье-оптике и фурье-голографии не только в математическом, но и в аппаратурном смысле. Рассмотрим этот вопрос в более общей форме. Основным методом фурье-оптики является воздействие на спектр пространственных частот изображений. Используемые для этой цели оптические схемы (когерентные Фурье-процессоры) фактически являются фильтрами пространственных частот. Если на входе фильтра пространственных частот расположено изображение 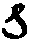 (x), имеющее спектр пространственных частот S(kx) по (5), то на его выходе формируется изображение (x), имеющее спектр пространственных частот S(kx) по (5), то на его выходе формируется изображение 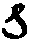 '(x) по спектрам S'(kx) /18/: '(x) по спектрам S'(kx) /18/:
Здесь В (kx) - комплексная характеристика пропускания фильтра пространственных частот. Учитывая, что диспергирующий элемент преобразует короткий световой импульс в движущееся изображение и что фильтр пространственных частот не чувствителен к
поперечному смещению изображения, придем к выводу, что любая ахроматическая система фильтрации пространственных частот может быть преобразована в систему фильтрации временных частот, если не ее входе и выходе поместить диспергирующие элементы, преобразующие временной сигнал в бегущее изображение и обратно. Характеристика пропускания полученного фильтра временных частот при этом будет равна Ф(Ω)=В(β Ω/ρ). Схема рис.3 представляет типичный (хотя и не единственный) пример преобразования пространственного фурье-процессора во временной Фурье-процессор. Аналогии пространственной и временной фильтрации были рассмотрены в /5-7/ и распространены на методы фурье-голографии в /12/.
Фурье-образ спектральной характеристики Ф(Ω) дает функцию временного отклика фильтрующей системы φ (t). Если функция пространственного отклика исходной системы пространственной фильтрации имеет вид b(t), то соответствующая функция временного отклика совпадает с b(t) no форме и равна φ(t)=const b(ct/β). Если r(t) - временной сигнал, падающий на вход спектрального процессора, то преобразованный сигнал на выходе имеет вид:
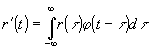 . (11) . (11)
Формула вида ( 11) хорошо известна в теориях линейных динамических систем, например, в теории электрических фильтров. Однако необходимо отметить существенное отличие. Электрический фильтр является системой, сосредоточенной в пространстве, поэтому на его функцию отклика накладывается требование неопережающего отклика, т.е. φ(t)=0 при t>0. Это требование иногда рассматривают как следствие причинности хода событий. В системе фильтрации временных частот, основанной на фурье-оптике, функция временного отклика φ(t) вытекает из функции пространственного отклика β(t), для которого оба направления оси x равноценны. Следовательно, в системах фильтрации временных частот, основанных на фурье-оптике, требование неопе-
режающего отклика в общем случае отсутствует. Это, на первый взгляд, парадоксальное утверждение, конечно, не приводит к нарушению причинности. Действительно, система фильтрации временных частот с помощью спектрального прибора, типа изображенного на рис.3, отличается от электрического фильтра тем, что не является сосредоточенной системой. Более того, именно рассредоточенность оптической системы в пространстве является необходимым условием спектрального разложения света.
Спектральная фильтрация оптического импульса происходит в результате дифракции или рефракции волны его спектрального разложения на амплитудных или фазовых транспарантах, помещаемых в плоскость спектра s (рис.3). При этом возможно как удлинение, так и укорочение пути оптического излучения, проходящего сквозь прибор, т.е. возникновение как запаздывающего, так и опережающего отклика. Примером может служить рассмотренное выше восстановление спектральных голограмм.
Вместо требования неопережающего отклика в оптических системах спектральной фильтрации существует требование ограниченного диапазона отклика, вытекающее из апертурных ограничений. Полный диапазон времени, в течение которого φ (t) отличается от нуля, не должен превышать 2Т.
Рассмотренные аналогии с фурье-оптикой и фурье-голографией создают возможности построения столь же гибкой, как и фурье-оптика, системы преобразования временных оптических сигналов. Эта система может быть названа импульсной фурье-оптикой /12/.
Отметим один из примеров аналогии фильтрации временных и пространственных частот, относящийся к созданию согласованных фильтров. Если сигнал r(t) обладает спектром R(Ω), то, как известно, идеальный согласованный фильтр имеет характеристику R*(Ω) /19/. В технике электрических цепей построение согласованного фильтра для временного сигнала произвольной формы является довольно громоздкой задачей. В фурье-оптике задача построения согласованного фильтра пространственных частот для сколь угодно сложных изображений решается очень просто голографическим методом Вандер-Люгта /18/. Метод Вандер-Люгта может быть перенесен на временные сигналы. Действительно, спектральная
голограмма (8) автоматически содержит согласованный по отношению к сигналу ra(t) фильтр Ra*(Ω). При восстановлении такой голограммы некоторым сигналом rc(t) возникает спектральный сигнал Rc(Ω)Ra*(Ω), которому на выходе прибора соответствует временной сигнал, совпадающий по форме с функцией корреляции сигналов rc(t) и ra(t). Как известно, вид функции корреляции служит признаком опознавания сигнала rc(t) по отношению к записанному на голограмме сигналу rа(t). Поэтому голограмма (8) может рассматриваться как временной аналог фильтра Вандер-Люгта и может использоваться для опознавания временных сигналов, аналогично опознаванию изображений в фурье-оптике /12/.
7. Рассмотрим некоторые возможности нелинейных преобразований сверхкоротких импульсов, основанные на взаимодействии волн их спектрального разложения /15/.
С помощью надлежащим образом построенных оптических систем и правильного временного согласования вблизи одной и той же плоскости спектра могут быть совмещены в пространстве и времени спектральные разложения (4) нескольких световых импульсов. На ту же плоскость могут быть, кроме того, спроектированы неподвижные монохроматические изображения. Считая, что волны спектральных разложений, принадлежащие разным импульсам, обладают одинаковой продолжительностью, запишем одну из них в виде:
Uj(t,x,z)=Gj (x)exp[i(ωoj+αjx)( 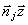 /c-t)]. (12)
Волна (12) может распространяться в положительном либо отрицательном направлении оси z, что учитывается введением в (12) произведения единичного вектора направления волны 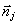 и векторной координаты и векторной координаты 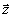 . Принадлежащие разным излучениям волны (12) могут отличаться направлением . Принадлежащие разным излучениям волны (12) могут отличаться направлением 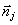 несущей частотой ωoj и дисперсией спектрального разложения αj несущей частотой ωoj и дисперсией спектрального разложения αj. Если положить α=0, то получим, что (12) фактически описывает волны, создаваемые некоторым монохроматическим изображением, причем частота излучения равна ωoj. С целью единообразия мы будем
рассматривать в этом случае (12) как результат оптического Фурье-преобразования некоторого исходного изображения 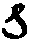 (х). Тогда при α=0 можно считать, что (х). Тогда при α=0 можно считать, что Gj(х)=S(γх), где S(kx) - спектр пространственных частот исходного изображения 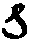 (х), определяемый аналогично (5). (х), определяемый аналогично (5).
Заполним окрестности плоскости спектра оптически нелинейной средой, в которой могут взаимодействовать волны спектрального разложения и монохроматические волны (12). Продольный размер нелинейной среды не должен превышать минимальной глубины резкости (ближней зоны дифракции), отвечающей одной из волн (12).
Создаваемая при взаимодействии излучений (12) волна нелинейной поляризации в простейших случаях определяется произведением амплитуд и сопряженных амплитуд исходных волн, которое зависит от типа используемой нелинейности и имеет следующий общий вид:
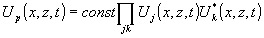 . (13) . (13)
Нетрудно видеть, что волна нелинейной поляризации Up(x,z,t) описывается выражением, аналогичным (12), т.е. имеет веерообразный вид. Если соблюдены условия пространственного синхронизма (условия Брэгга), то волна нелинейной поляризации эффективно генерирует новую световую волну, которая также имеет веерообразный вид и описывается выражением (12) с некоторыми новыми значениями характеристик: Gp(x), ωор, αр, 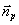 . При этом происходит алгебраическое сложение несущих частот ωoj и дисперсий αj исходных волн, а также умножение распределений Gj(x) и Gj*(x). Если результирующее значение α≠0, то генерируемое излучение можно рассматривать как спектральное разложение некоторого волнового пакета. При α=0 фактически генерируется монохроматическое изображение, которое мы будем рассматривать как спектр пространственных частот некоторого нового изображения. Новый волновой пакет или новое изображение могут быть сформированы с помощью спектрального прибора с нужными характеристиками или соответствующей фурье-оптической схемы. . При этом происходит алгебраическое сложение несущих частот ωoj и дисперсий αj исходных волн, а также умножение распределений Gj(x) и Gj*(x). Если результирующее значение α≠0, то генерируемое излучение можно рассматривать как спектральное разложение некоторого волнового пакета. При α=0 фактически генерируется монохроматическое изображение, которое мы будем рассматривать как спектр пространственных частот некоторого нового изображения. Новый волновой пакет или новое изображение могут быть сформированы с помощью спектрального прибора с нужными характеристиками или соответствующей фурье-оптической схемы.
В общем случае нелинейные взаимодействия приводят к перемножению спектров временных и пространственных частот, поэтому их результатом должны быть математические операции корреляции и свертки исходных временных и пространственных сигналов, генерируемые в виде нового временного или пространственного сигнала.
По-видимому, эти возможности могут быть реализованы наилучшим образом при четырехволновых нелинейных взаимодействиях, которые можно рассматривать как процесс динамической голографии волн спектрального разложения. Пусть на нелинейную среду падают три излучения, любое из которых может быть спектральным разложением короткого импульса либо разложением в спектр пространственных частот одномерного изображения. Частота осцилляции нелинейной поляризации для любого из сечений х= const может быть представлена следующей алгебраической суммой частот взаимодействующих излучений:
ω р=ω1+ω2-ω3,
где 1,2,3 - индексы, присвоенные трем исходным волнам. Этому соотношению соответствует следующее правило умножения амплитуд:
Gp(x)=G1(x)G2(x)G3*(x), (14)
где Gp(x) - распределение амплитуды генерируемого излучения. Введем общее определение фурье-образа для всех четырех амплитуд:
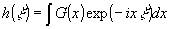 . .
В случае монохроматического сигнала g(x)~s(-ξ/γ), а в случае волнового пакета g(ξ)~r(ξ/α).
Из (14) вытекает
h(ξ)~h 1(ξ)Ä
h2(ξ)*h3(ξ), (15)
где Ä
и * обозначают операции свертки и корреляции /18/. Поскольку любая из функций, входящих в (15), может быть временным
либо пространственным сигналом, то в целом возникают довольно широкие возможности преобразований этих сигналов. Отметим наиболее существенные из этих возможностей ( см. /12/): а) сокращение или удлинение временного сигнала при сохранении его формы; б) динамическое обращение сигнала во времени; в) преобразование временного сигнала в пространственный и обратное преобразование, т.е. модуляция/демодуляция телевизионного типа.
8. Интересные возможности пространственно-временных преобразований возникают при использовании нелинейных взаимодействий волн спектрального разложения (3), (4) с плоской монохроматической волной /17/. Эти взаимодействия приводят к формированию в нелинейной среде нестационарных голографических решеток, обладающих чрезвычайно высокой скоростью линейного или углового перемещения. Так, в результате взаимодействия бегущего луча (3) с встречной плоской монохроматической волной возникает нестационарная решетка следующего вида (рис.5а):

а) б)
Рис.5. Голографические элементы для сверхбыстрого сканирования световых лучей:
"бегущее зеркало" (а) и "вращающееся зеркало" (б).
H(t,x,z1 )~r[t-(βx+z1)/c](cos2k 0z 1+1) (16)
(предполагается, что r(t) - вещественно). Решетка (16) обладает отражательными свойствами. Затем, что поскольку скорость поперечного перемещения решетки (16) сопоставима со скоростью света, то отражательные свойства различны для излучений, падающих на решетку попутно или встречно по отношению в формирующему ее импульсу. Так, если на решетку рис.5а слева падает плоский волновой пакет, то в отраженном излучении на плоскости F формируется неподвижное изображение, которое является пространственным аналогом временного сигнала, содержащегося в волновом пакете. Если же справа на решетку рис.5а фокусируется неподвижное монохроматическое изображение, то в отраженном свете формируется бегущий по плоскости F излучатель, амплитуда излучения которого в каждой точке пропорциональна амплитуде пространственного сигнала. Такой сигнал может быть легко преобразован во временной аналог исходного изображения.
Рассмотрим теперь взаимодействие волны спектрального разложения (4) с направленной навстречу плоской монохроматической волной. Считая, что R(Ω)≈const, получим в результате интерференции волн нестационарную решетку следующего вида:
H(x,z,t)~cos[2k0 z+αx(z/c-t)]+1. (17)
Эта решетка содержит веерообразную структуру, которая вращается вокруг точки фокуса 0 с угловой скоростью α /2k0, в два раза меньшей, чем скорость вращения волны спектрального разложения. Такую решетку можно рассматривать как быстро вращающееся зеркало. Веерообразность решетки компенсирует доплеровские эффекты, возникающие при отражении волн от такого вращающегося зеркала. Как и в случае решетки (16),отражательные свойства решетки (17) зависят от направления падения на нее излучения. При
падении на решетку рис.5б слева плоского волнового пакета, несущего временной сигнал, происходит развертка этого сигнала, аналогичная развертке вращающимся зеркалом в устройствах фотохронографии. При этом в дальней зоне формируется изображение, которое является аналогом исходного временного сигнала.
Пусть на решетку рис.5б падает справа монохроматическое излучение, формирующее на плоскости S некоторое изображение. При отражении света от движущихся слоев решетки формируется вращающаяся волна, модулированная в поперечном направлении исходным изображением. Эту волну можно рассматривать как волну спектрального разложения некоторого импульса, амплитудный спектр которого является аналогом исходного пространственного сигнала.
Таким образом, динамические голограммы волн спектрального разложения сверхкоротких импульсов можно использовать как голографические оптические элементы, перемещающиеся со скоростями, недоступными устройствам с механическим перемещением. Это позволяет осуществлять пространственно-временные преобразования оптического излучения с весьма высоким разрешением во времени. Нетрудно показать, что временное разрешение единичного дифракционного элемента изображения при рассмотренных пространственно-временных преобразованиях равно длительности сверхкороткого импульса, с помощью которого формируется движущаяся решетка, и может достигать, например, 10-12-10 -14 с.
Л и т е р а т у р а
1. Мазуренко Ю.T. Оптика и спектроскопия, 1985, т.59, с.606.
2. Борн М., Вольф Э. Основы оптики. М., Наука, 1970, с.855.
3. Дитчберн Р. Физическая оптика. М., Наука, 1965, с.200.
4. Малышев В.И. Масалов А.В., Сычев А.А. ЖЭТФ, 1970, т.59, с.48.
5. Froehly Cl., Colombeau R., Vampouille M. In:
"Progress in Optics", ed.E.Wolf.-Amst.-London North Holl.publ.press, 1983, 20, р.63.
6. Froehly Cl., Lacourt A., Vienot J.Ch. Nouv.Rev.Optique, 1973, 4, р.133.
7. Froehly Cl., Journ. of Optics, 1981, 12, p.25.
8. Зубов В.А., Крайский А.В., Кузнецова Т.И. Письма ЖЭТФ, 1971, т.13, с.443.
9. Зубов В.А., Кузнецова Т.И. Квантовая электроника, 1973, №1, с.135.
10. Rebane A., Kaarly R., Saari P., Anijalg A., Timpmann K., Opt.Commun., 198 3, 47, р. 1737.
11. Мазуренко Ю.T. Оптика и спектроскопия, 1984, т.56, с.583.
12. Мазуренко Ю.T. Оптика и спектроскопия, 1984, т.57, с.8.
13. Мазуренко Ю.T. Письма ЖГФ, 1984, т.10, с.539.
14. Мазуренко Ю.T. Квантовая электроника, 1985, т.12, с.1235.
15. Мазуренко Ю.T. Оптика и спектроскопия, 1985, т.59, с.57.
16. Мазуренко Ю.T. Оптика и спектроскопия, 1985, т.59. 608.
17. Мазуренко Ю.T. Оптика и спектроскопия, 1986, т.60. с.551.
18. Сороко Л.М. Основы голографии и когерентной оптики. М., Наука, 1971, с.200.
19. Папулис А. Теория систем и преобразований в оптике. М., Мир, 1971, с.300.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

