|
|
 |
 |

|
| |
КИНЕМАТИЧЕСКИЙ МЕТОД СОЗДАНИЯ ГОЛОГРАФИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ УГЛА
Е.П.Кривцов, Д.П.Лукьянов, Ю.В.Филатов
Рассматривается метод создания шкал дискретных преобразователей угла, заключающийся в регистрации носителем записи интерференционного поля, образованного выходящими лучами вращающегося кольцевого лазера. Приводятся оценки разрешающей способности и погрешности шкал.
Голографические методы получили широкое распространение при создании оптических элементов - дифракционных решеток, шкал, сеток. Фоторегистрация интерференционной картины, образованной двумя плоскими волнами позволяет получить периодические структуры с разрешением u
, ограниченным лишь волновой природой света (для he-ne лазера u
max »
3000). Размеры таких структур ограничены апертурой коллимирующей оптики, а также плотностью лазерного излучения, необходимой для экспонирования фотоматериала, и не превышает обычно 100 мм. Для преобразователей линейных перемещений, широко применяемых в прецизионном машиностроении, необходимы шкалы длиной до 1 м и более. Метод фазового согласования интерференционных полей с помощью подвижкой голографической решетки, имеющий точность не хуже l
/100, позволяет путем последовательного экспонирования с наложением получать достаточно длинные шкалы без ухудшения их качества /1,2/.
При этом отдельные участки шкалы формируются в интерференционном поле двух квазиплоских волн, которые обратят на соответствующем носителе амплитудную или фазовую линейную дифракционную решетку.
Перенесение этого же принципа на формирование радиальных решеток для построения преобразователей угловых перемещений встречает определенные затруднения как при синтезе волновых фронтов интерферирующих волн, так и при "сшивания" отдельных участков локального экспонирования и, особенно, при замыкании радиальной решетки
- 207 -
самой на себя. Действительно, интерференция квазиплоской и сферической волн позволяет получить радиальное распределение полос только на сравнительно небольших угловых участках шкалы, которая при этом имеет, как правило, достаточно большой диаметр. Это увеличивает по сравнению с линейной шкалой число необходимых фазовых согласовании, а, следовательно, и время нанесения шкалы. Ухудшение качества фазового согласования при угловом наложении двух интерференционных полей, а также необходимость искусственного замыкания круговой шкалы существенно усложняют процесс ее создания.
Преодолеть указанные недостатки можно переходом к кинематическим методам голографии, при которых интерферирующие волны изменяют свои характеристики, а сама интерференционная картина перемещается относительно регистрирующей среды.
Один из возможных вариантов метода иллюстрируется рис.1 /3/.

Рис.1.
Здесь кольцевой газовый лазер (КГД), образованный зеркалами 1-4 и активным элементом 5, вращается вокруг оси ОС, перпендикулярной плоскости резонатора, с угловой скоростью W
. Выходящие через зеркала 1 и 4 встречные волны КГЛ направляются зеркалами 6 и 7 на неподвижный носитель записи 8, где они образуют интерференционную
- 208 -
картину в точке 9, удаленной от оси вращения на расстояние r. Известно /4/, что при вращении КГЛ с частотой W
разность частот встречных волн удовлетворяет соотношению:
w
1 - w
2 = 2p
4sW
/l
l
где s, l -площадь и периметр резонанса КГЛ, соответственно; l
- средняя длина волны.
Интенсивность поля интерференции встречных волн в неподвижной системе координат может быть в виде /5/:
i(x,y,t) = e21 + e22 + 2e1e2cos[(w
1 - w
2)t – xa cosW
t - yasinW
t] (2)
где a = 2p
/b, b - ширина полосы интерференционной картины;
Таким образом, при вращении КГЛ интерференционная картина вместе с ним перемещается по носителю записи 8, описывая окружность радиуса r, а внутри нее интерференционные полосы смещаются со скоростью, которая может быть найдена из соотношения (2). Если добиться синхронизма, при котором скорость перемещения результирующего поля по поверхности носителя равна по модулю скорости смещения интерференционных полос, то последние окажутся неподвижными относительно носителя 8 и при достаточной интенсивности интерферирующих волн дифракционная решетка может быть записана за один оборот КГЛ.
Условия синхронизма могут быть представлены в виде ' '
a
= arcsin[kl
/4p
r] (3)
где a
- угол сведения лучей в точке 9, К = 2p
4s/l
l - масштабный коэффициент КГЛ.
Минимальное время экспозиции t определяется кинематикой движения результирующего интерференционного поля и радиусом пятна
t
= ℓrW
(4)
С учетом выражения (4) можно определить требуемую чувствительность носителя записи b
b
= p/p
ℓrW
где Р - мощность пучке, выходящего из КГЛ.
Принимая Р = 1 мВт, ℓ = 0,5 мм, W
= 1 с-1 и r = 100 мм, получаем b
= 1,3·10-5 Дж/мм2.
- 209 -
Чувствительность рядя галоидосеребряных эмульсий (микрат ЛОЙ-2, ПВ-1, ВРМ и др) оказывается достаточной для кинематической записи результирующего поля за один оборот.
При сравнительно высоких угловых скоростях движения интервал флуктуаций параметров КГЛ может быть много меньше времени одного оборота, что создает необходимые условия для "сшивания 1' шкалы и создания прецизионных преобразователей "угол-код". По существу, рассматриваемый метод позволяет "перенести" поле из резонатора КГЛ на соответствующую регистрирующую среду. Действительно, можно показать /6/, что в кольцевом резонаторе газового лазера встречные волны образуют интерференционное поле, которое своими характерными точками (узлами и пучностями) делят периметр l КГЛ на n=2l/l
равных частей. Оставаясь при вращении КГЛ неподвижный в инерциальном пространстве, интерференционное поле играет роль высо-коразрешающей угловой шкалы, которая и переносится в рассматриваемом методе на регистрирующую среду. При этом независимо от радиуса r образуемой шкалы общее число штрихов при постоянных параметрах КГЛ остается неизменным и равным масштабному коэффициенту КГЛ.
На основании изложенного можно сделать вывод, что одна из основных характеристик сформированного гадим образом преобразователя угол-код, а именно, дискретность (или угловая цена деления шкалы), полностью определяется масштабным коэффициентом КГЛ и составляет величину 0,б...1 утл.с. При обычной для фотоэлектрических преобразователей интерполяции шага шкалы на конечное число частей n (n = 10…100) это позволяет получить разрешение в сотые доли угловой секунда.
Важной характеристикой шкалы, создаваемой интерференционным методом, является контрастность и ее зависимости от радиуса шкалы и ширины интерференционного пятна. Интегрирование выражения (2) за время экспозиции t
дает следующее выражение для результата регистрации интерференционной картины носителем записи:
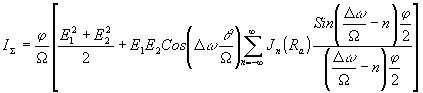 (5) (5)
- 210 -
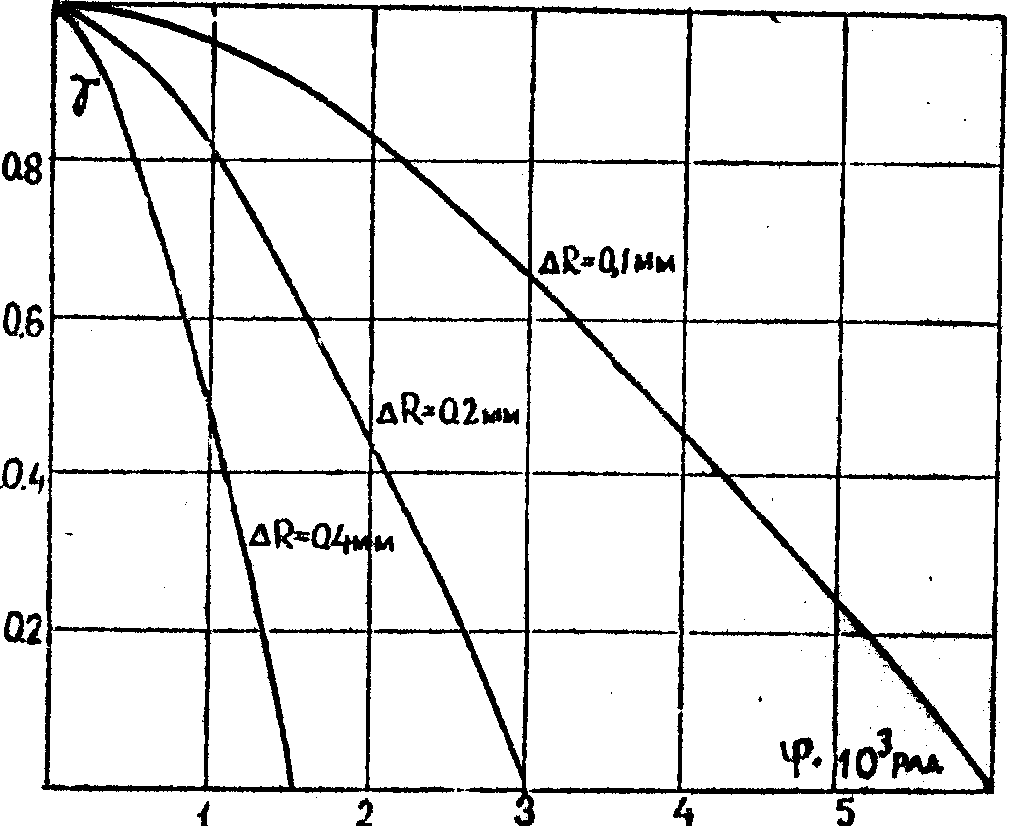
Рис.2.
- 211 -
где j
- угол, под которым видно интерференционное пятно центра вращения, D
w
=w
1-w
2. Координаты точек полученной шкалы задаются радиусом r и углом наблюдения q
. Очевидно, что в идеальном случае зависимость величины iå
от угла q
должна быть чисто гармонической с амплитудой, равной Е1Е2. Следовательно, множитель перед косинусом во втором слагаемом выражения (5) определяет контрастность шкалы
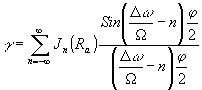 (6) (6)
Анализ показывает, что при r, равном величине r0, определяемой условием "синхронизма" (3), контрастность определяется величиной j
и приближенно может быть определена как
g
~ [1 - j
3/12]
Такая зависимость обусловлена различием угловой цены ширины интерференционной полосы в центре пятна и на его периферии. При отклонении r от r0 на величину D
r контрастность спадает как
g
~ [1 – (D
raj
)2/12]
Характер зависимости контрастности от угловой ширины пятна j
и радиуса шкалы r приведен на рис.2. Для пучка диаметром ℓ = 0,5 мм при r = 100 мм можно получить контрастность g
³
0,5, если длину штрихов шкалы ограничить величиной 0,1 мм. Специфика рассматриваемого метода, заключающаяся в проведении записи шкалы за один оборот КГЛ, приводит к зависимости погрешности шкалы как от систематических, так и от случайных внутриоборотных погрешностей КГЛ. Сведения о внутриоборотных погрешностях можно получить из анализа результатов угловых измерений, проводимых с помощью КГЛ на динамическом гониометре, схема которого представлена на рис. 3 /6/.
В данной схеме КГЛ 1 вращается вместе с многогранной призмой 2 и его выходной сигнал заполняет на счетчике 4 интервалы между импульсами, снимаемыми с автоколлимационного нуль-индикатора 3. Таким образом происходит измерение углов между гранями призмы j
i. В том случае, когда многогранная призма предварительно аттестована
- 212 -
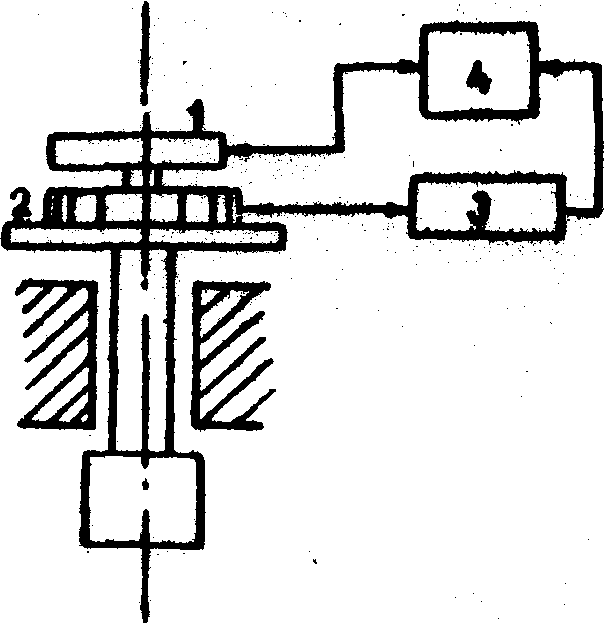
Рис.3.
и с высокой точностью известны значения углов между ее гранями j
ati, отличие значения, полученных в помощью КГЛ, от известных (j
i - j
ati) дает информацию о погрешностях КГЛ. При этом следует учитывать, что существенный вклад в величину j
i - j
ati могут вносить погрешности аттестации многогранной призмы и погрешности нуль-индикатора. Относя, тем не менее, всю погрешность к КГЛ, мы можем оценить верхний предел его погрешностей. Результаты экспериментов, проведенных в работах /7,8/, 'показали, что величина j
i - j
ati - не превышает 0,2...0,4 угл.с. во всем диапазоне измеряемых углов.
С целью исключения погрешности аттестации многогранной призмы были проведены эксперименты на гониометре, в котором нуль-индикатор
- 213 -
содержал два опорных направления, неизвестный, но постоянный угол между которыми подлежал измерению. Многогранная призма в этом случае /9/ играет роль сканирующего устройства и погрешность ее аттестации несущественна. В качестве нуль-индикатора вместо автоколлиматора использовался интерферометр, менее чувствительный к таким источникам систематических погрешностей, как пирамидальность многогранной призмы и ее эксцентриситет. Для КГЛ, имеющего цену импульса 1,3 угл.с. при измерениях внешних углов в диапазоне 5 ¸
10° отклонения от среднего значения внутри оборота, не превысили 0,12 угл.с. При этом указанное значение содержит вклад как систематических, т.е. повторяющихся от оборота к обороту, так и случайных погрешностей КГЛ. Минимальный уровень случайных погрешностей КГЛ определяется естественными шумами и составляет сотые доли угловой секунды /6/. Приведенные результаты экспериментальных исследований позволяют оценивать потенциальную погрешность голографического преобразователя угла на уровне сотых долей угловой секунды, а реальную погрешность менее одной десятой угловой секунды.
Таким образом, проведенный анализ показал, что рассмотренный метод позволяет создавать шкалы дискретных преобразователей угла за один оборот КГЛ и дискретностью порядка 1 угл.с. и погрешностью на уровне 0,1 угл.с. Детальный анализ наряду с проведением экспериментальных исследований позволит, по-видимому, перейти к широкому использованию рассмотренного метода в качестве эффективного средства создания голографических дискретных преобразователей угла.
Литература
1. Турухано Н. Исследование голографических измерительных систем. Канд. дис. Л., 1975.
2. Гордеев С.В., Горелик В.П., Турухано Б.Г., Турухано Н. Подвижная голографическая решетка как измерительный элемент при исследовании интерференционного поля. Препринт ЛИЯФ-683, Л., 1981 с.4.
3. Лукьянов Д.П., Мелехов П.В., Филатов Ю.В., Щербаков С.a. Устройство для разметки угловых шкал. АС № 918785, Б.И., № 13, 1982.
- 214 -
4. Бычков С.И., Лукьянов Д.П., Бакаляр А.И. Лазерный гироскоп. - М.: Советское радио, 1975. -424 с.
5. Лукьянов Д.П., Филатов Ю.В. Особенности интерференции встречных волн кольцевого лазера в не" связанной с ним системе координат. -Оптика и спектроскопия, 1983, т.54, в.6, с.1083-1086.
6. Лазерные измерительные системы. Под ред. Д.П.Лукьянова. -М.: Радио и связь, 1981, 456 с.
7. Блантер Б.Э., Филатов Ю.В. Экспериментальное исследование точности измерительного преобразователя на основе кольцевого лазера. - Метрология, 1979, № 1, с.3-8.
8. Ванюрихин А.И., Зайцев И.И. Автоматизированный гониометр на основе кольцевого лазера. -ОМП, 1982, № 9, с.28-31.
9. Бородавко К.П., Мелехов П.В., Филатов Ю.В. Исследование угловых уходов стабилизированных объектов с помощью лазерного гониометра. -Изв. ЛЭТИ, 1982, вып.307, с.76-80.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

