|
|
 |
 |

|
| |
ПИМЕНИНИЕ ГОЛОГРАФИИ И ИНТЕРФЕРОМЕТРИИ ДЛЯ ИССЛЕДОВАНИЯ КАЧЕСТВА ИЗОБРАЖЕНИЯ КОГЕРЕНТНЫХ ОПТИЧЕСКИХ СИСТЕМ
К.Г.Предко, В.Г.Синченко
Дан краткий обзор известных интерферометрических методов определения когерентных передаточных характеристик (kПx) оптических систем. Приведены экспериментальные результаты по исследованию КПХ, а также функций размытия линии объективов для разных дефокусировок. Найдено, что требование к точности совмещения плоскостей регистрации изображения и наилучшей фокусировки при когерентном освещении выше, чем при некогерентном. Показана возможность упрощения методики измерения КПХ с причинением голографического метода регистрации волнового фронта.
Использование когерентного освещения в различных областях , связанных с получением изображения, требует определения характеристик, формирующих изображение систем для этого случая освещения. Критерий разрешающей способности является неудовлетворительным. Он необъективен (зависит от наблюдателя) и при наличии когерентности неоднозначен (зависит от разности фаз волн, испускаемых двумя точками) /1/. Кроме того, данные о разрешающей способности не дают информации о передаче оптической системой крупных деталей. Характеристика оптических систем должна быть объективной, измеряемой, пригодной для определения характеристик каскадных систем различного назначения /2/. Для некогерентного освещения этим условиям удовлетворяет оптическая передаточная функция или связанная с ней функция размытия точки. При когерентном освещении оптическую систему характеризуют аналогичными когерентными передаточными характеристиками (КПХ): когерентной передаточной функцией или амплитудной функцией размытия точки. При экспериментальном их определении чаще используют одномерную когерентную передаточную
- 164 -
функцию и амплитудную функцию размытия линии. Эти характеристики позволяют: а) учитывать искажение амплитуды и фазы поля, вносимые системой; б) определить разрешающую способность системы для разных условий освещения; в) рассчитывать освещенность в изображении системой различных объектов; г) сравнивать различные системы между собой.
Цель данной работы - дать краткий обзор известных методов определения КПХ, формирующих изображение систем, указать их достоинства и недостатки, показать возможности голографии при определении КПХ сложных, включающих мутную среду систем, а также привести некоторые экспериментальные результаты по исследованию -КПХ объективов.
КПХ линзовых систем могут быть определены интерферометрическими методами из данных о зрачковых функциях систем, используя взаимосвязь этих функций /1/. В связи с этим, интерферометрические метода и приборы, применяемые для нахождения функции зрачка, могут применяться к исследованию КПХ. К ним относятся интерферометры типа Тваймана-Грина и неравноплечий лазерный интерферометр /3/. Достоинство данных приборов - двумерность получаемых КПХ, высокая точность, возможность автоматизации. Для повышения точности в рабочее плечо интерферометра Тваймана-Грина вводят интерферометр Фабри-Перо /4/. К недостаткам - сложности юстировки, расшифровки интерферограмм, высокая стоимость, трудности применения к исследованию КПХ систем, включающих мутные среды.
Исследования КЛХ различных оптических систем можно выполнять, применяя метод Линника /5/. Суть его заключается в анализе интерференционной картины, возникающей вследствие интерференции прошедшей изучаемую систему волны со сферической волной. Сферическая волна формируется в результате дифракции параксиальных пучков на отверстии в полупрозрачной пластине, расположенной в плоскости изображения, когда объектная волна распространяется через пластину. Достоинства данного способа определения КПХ простота элементарной базы установки, низкие требования к виброзащищенности. Недостатками способа является: необходимость учёта искажений, вносимых подложкой пластины, возможность исследовании только небольших деформаций волнового фронта, малый контраст полос при исследовании
- 165 -
систем, включающих мутные среды.
Следует остановиться на методе анализа фазовых распределений в лазерных пучках /6/. Сущность метода состоит в следующем. С помощью двух отверстий выделяют две точки исследуемого пучка и фиксируют при этом положение интерференционных полос, возникающих за отверстиями. Фиксацию проводят с помощью фотоумножителя и расположенной перед ним диафрагмы. Затем перемещают отверстия с шагом, равным расстоянию между ними. Одновременно перемещают на эту же величину и фотоумножитель с диафрагмой. Измеряя при этом интенсивности от двух отверстий и от каждого из отверстий в отдельности, можно рассчитать разность фаз колебаний, выходящих из каждой пары рассматриваемых точек, а затем найти распределение разности фаз для любых пар точек.
В отличие от ранее рассмотренных, в методе /6/ не требуется создания референтного пучка точно известной формы. Это обеспечивает высокую точность получаемых данных. Однако, применительно к исследованию КПХ систем использовать этот метод технически трудно вследствие малых размеров пятен размытия. Кроме того, постоянство расстояния между отверстиями затрудняет исследование фазовых поверхностей сложной формы.
Нахождение зрачковой функции, а равно и КПХ оптической системы, можно выполнить топографическим методом /7/. Его также применяют и для определения оптических передаточных функций /8/. По этому методу для нахождения КПХ в фокальную плоскость исследуемой системы помещают точечный источник и с помощью когерентного референтного пучка одновременно на двух фотопластинках регистрируют две голограммы прошедшего систему пучка. При восстановлении голограммы располагаются в одной плоскости, освещаются референтным пучком, применяемым при записи, а затем смещаются одна относительно другой. В результате за общей областью перекрытия голограмм будет наблюдаться картина, возникающая вследствие интерференции восстановленных из голограмм пучков. Форма полос этой картины зависит как от аберраций исследуемой системы, так и от величины сдвига голограмм. На получаемый результат, кроме того, влияет стабильность установки, а также свойства регистрирующего материале, и условия его обработки /9/.
- 166 -
Из обзора указанных работ следует, что в настоящее время существуют хорошо разработанные методы, а также аппаратура для определения КПХ различных линзовых систем типа объективов. В то же время для ряда задач гидрооптики, атмосферной оптики требуется исследование КПХ каскадных систем, одним из элементов которых является мутная или турбулентная среда. Применение описанных выше методов и приборов к решению такого рода задач встречается со значительными трудностями. В связи с этим, разработка простых, не требующих дорогостоящего оборудования методов, позволяющих исследовать КПХ сложных систем, включающих мутные и турбулентные среды, представляется актуальной задачей.
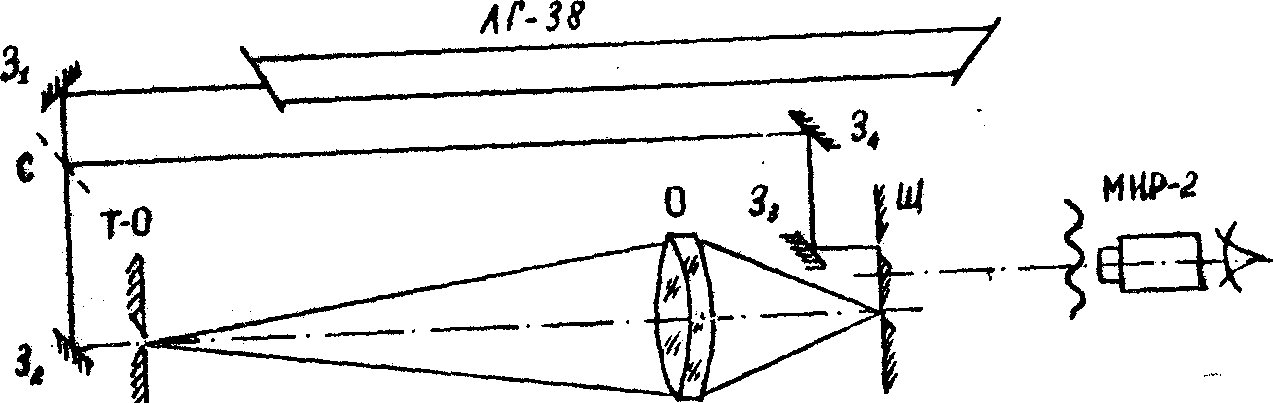
Для решения указанных задач в /10/ предложен метод определения КПХ, пригодный для исследования КПХ систем различного назначения. В данной работе этим методом исследовались такие КПХ, как амплитудная функция размытия линии (АФРЛ) двухлинзовото объектива при его различных относительных отверстиях и положениях плоскости регистрации. Оптическая схема установки приведена на рис.1а. Пучок света от лазера ЛГ-38 расщепляется светоделителем С на два пучка. Один из пучков направляется на тест-объект Т-О, щель шириной 3 мкм и высотой 3 мм. Дифрагировавший на этой щели пучок попадает на исследуемый объектив О. В плоскости изображения Т-О размещается одна из двух анализирующих щелей Щ. Их ширина 2 мам, высота - 2 мм, расстояние между ними - около 1 мм. Во вторую щель Щ посредством системы зеркал З1-З4, направляется отраженный светоделителем пучок. За щелями Щ, с помощью микроскопа МИР-2, наблюдается интерференционная картина. Смещение полос этой картины n(u), при сканировании пятна размытия, определяет фазу АФРЛ j
(u). Для определения модуля АФРЛ h(u) необходимо измерить интенсивность в изображении линии i0(u) и модуль степени когерентности между различными точками пятна размытия линии в второй анализирующей щелью, координата которой а. Обозначая через nl
число смещенных полос, соответствует изменению разности фаз на длину волны l
, h(u) и j
(u) можно определить из соотношений:
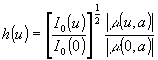 , j
(u) = 2p
n(u)/nl
(1) , j
(u) = 2p
n(u)/nl
(1)
- 167 -
а)
б)
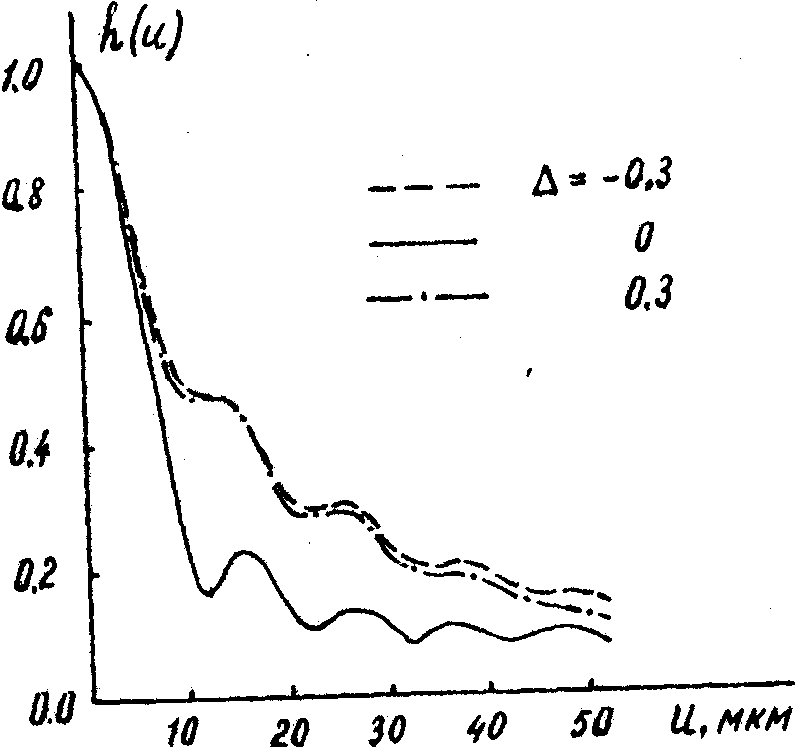
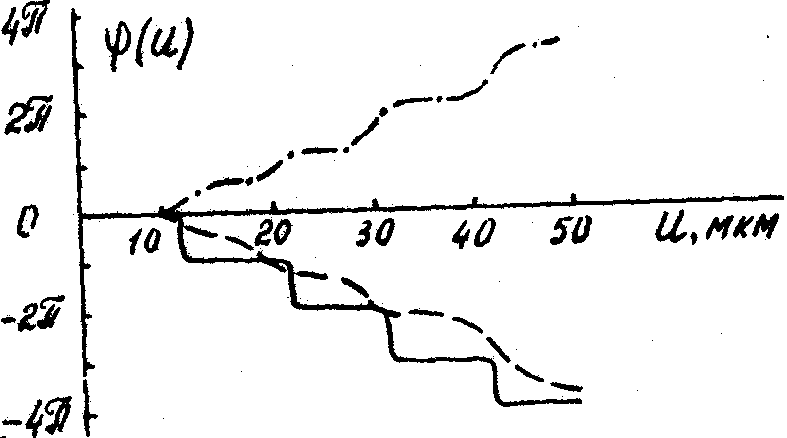
Рис.1. а).0птическая схема установки исследования КПХ объективов, б) модуль h(u) и фаза j
(u) АФРЛ дифракционно ограниченного объектива для разных дефокусировок D
(мм).
- 168 -
Для определения i0(u) и |
m
(u,a)|
за анализирующими щелями располагался фотоумножитель с расположенной перед ним диафрагмой. Её размеры обеспечивали разрешение интерференционной картина.
Таким образом были найдены АФРЛ объектива с фокусным расстоянием 135 мм при отображении тест-объектива с расстояния 550 мм. Перед объективом располагались диафрагмы размером 1 и 3 см. Угловая приемная апертура при этом составляла, соответственно, около 0,02 и 0,06 рад. На рис.1б для апертуры 0,02 рад приведены половины симметричных относительно оси ординат значений h(u) и j
(u) при разных дефокусировках D
. Знак D
считался положительным, если плоскость щелей Щ, удалялась за плоскость параксиального изображения. Как видно из этого рисунка, измеренные h(u) и j
(u) близки к h(u.) и j
(u) дифракционно ограниченной системы. Так, h(u) для D
= 0 имеет вторичные минимумы и максимумы освещенности. Минимумы наблюдаются в точках 10,5, 21,5, 32 и 43 мкм, что соответствует апертуре системы в плоскости изображения около 0,03 рад. При переходе от одною максимума к другому j
(u) измеряется, на p
. В пределах максимума j
(u) постоянна. Для D
= ±
0,З мм также наблюдаются максимумы и минимумы освещенности, однако, относительная интенсивность главного максимума по сравнению со вторичными меньше, чем для D
= 0. Фаза АФРЛ для D
=±
0,3 мм, как и h(u), симметрична относительно плоскости D
= 0, однако, резкие скачки при переходе от одного максимума к другому отсутствует. Данные эксперимента в этих случаях хорошо подтверждают теорию /11/.
Рассмотрим особенности определения АФРЛ, связанные с одномерной структурой тест-объекта. В отличие от точки, интенсивность в изображении которой не зависит or когерентности /12,13/ интенсивность в изображении линии является функцией когерентности освещающего линяю пучка. Действительно, спектр изображения бесконечно узкой линии Т(u
) связан со зрачковой функцией системы 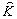 (u
1,u
'1) и функцией, описывающей спектр освещавшего пучка Т(u
'1)=ò (u
1,u
'1) и функцией, описывающей спектр освещавшего пучка Т(u
'1)=ò
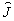 (u
",u
'1)du
", соотношением /13/: (u
",u
'1)du
", соотношением /13/:
t(u
) = ò
ò
t(u
'1)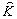 (u
1 + u
1u
'1) (u
1 + u
1u
'1)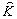 *(u
1,u
'1)du
1du
'1 (2) *(u
1,u
'1)du
1du
'1 (2)
- 169 -
Здесь 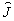 (u
",u
'1) - Фурье-преобразование по пространственным частотам u
" и u
'1 функции взаимной интенсивности (ФВИ) j источника; u
'1 - соответствует частоте вдоль щели. При некогерентном освещении, когда Т(u
'1) = const., выражение (2) переходит в соотношение, связывающее оптическую передаточную и зрачковую функции /2/. При когерентном и частично когерентном освещении зрачок системы модулируется функцией Т(u
'1). Например, при освещении узкой вдели когерентной плоской волной освещение за щелью имеет вид растянутого вследствие дифракции пятна; вдоль щели оно сохраняет свою угловую структуру. В результате на систему попадает волна, радиус кривизны которой соответствует в одном направлении расстоянию от щели до плоскости входного зрачка системы, в другом - бесконечности. При этом входной зрачок полностью заполнен только в одном направлении, В другом - заполнение определяется высотой щели и размером освещающего пучка. Таким образом, изображение щели. освещенной плоской волной, формируется частью входной апертуры системы. В случае некогерентного освещения щели, каждая её точка излучает сферическую волну, заполняющую всю апертуру, вследствие чего изображение щели формируется полной апертурой системы. Отсюда следует, что при наличии аберраций системы нормированные распределения интенсивности в изображении линии при когерентном sk(u) и некогерентном sh(u) освещении должны быть различимы. На рис.2 представлены половины распределений sk(u) и sН(u), полученные для апертуры 0,06 рад и осевых точек поля зрения, подтверждающие сделанные предположения. Случай некогерентного освещения реализовался с помощью освещения Т-О лампой накаливания через светофильтр КС-13. Как видно из рис.2, для D
=0 интенсивность для всех и при некогерентном совещании выше, чем при когерентной освещении. Если приёмную апертуру ограничить до размеров, соответствующих заполнению при когерентном освещении, то, как показывает эксперимент, sК(u) и sН(u) совпадают. Наблюдаемые длинные "крылья" sk(u) и sh(u) обусловлены значительной сферической аберрацией исследуемого объектива. График сферической аберрации объектива, полученный экспериментально, приведен на рис.2. (u
",u
'1) - Фурье-преобразование по пространственным частотам u
" и u
'1 функции взаимной интенсивности (ФВИ) j источника; u
'1 - соответствует частоте вдоль щели. При некогерентном освещении, когда Т(u
'1) = const., выражение (2) переходит в соотношение, связывающее оптическую передаточную и зрачковую функции /2/. При когерентном и частично когерентном освещении зрачок системы модулируется функцией Т(u
'1). Например, при освещении узкой вдели когерентной плоской волной освещение за щелью имеет вид растянутого вследствие дифракции пятна; вдоль щели оно сохраняет свою угловую структуру. В результате на систему попадает волна, радиус кривизны которой соответствует в одном направлении расстоянию от щели до плоскости входного зрачка системы, в другом - бесконечности. При этом входной зрачок полностью заполнен только в одном направлении, В другом - заполнение определяется высотой щели и размером освещающего пучка. Таким образом, изображение щели. освещенной плоской волной, формируется частью входной апертуры системы. В случае некогерентного освещения щели, каждая её точка излучает сферическую волну, заполняющую всю апертуру, вследствие чего изображение щели формируется полной апертурой системы. Отсюда следует, что при наличии аберраций системы нормированные распределения интенсивности в изображении линии при когерентном sk(u) и некогерентном sh(u) освещении должны быть различимы. На рис.2 представлены половины распределений sk(u) и sН(u), полученные для апертуры 0,06 рад и осевых точек поля зрения, подтверждающие сделанные предположения. Случай некогерентного освещения реализовался с помощью освещения Т-О лампой накаливания через светофильтр КС-13. Как видно из рис.2, для D
=0 интенсивность для всех и при некогерентном совещании выше, чем при когерентной освещении. Если приёмную апертуру ограничить до размеров, соответствующих заполнению при когерентном освещении, то, как показывает эксперимент, sК(u) и sН(u) совпадают. Наблюдаемые длинные "крылья" sk(u) и sh(u) обусловлены значительной сферической аберрацией исследуемого объектива. График сферической аберрации объектива, полученный экспериментально, приведен на рис.2.
Распределения sК(u) и sh(u ) для разных D
также
- 170 -
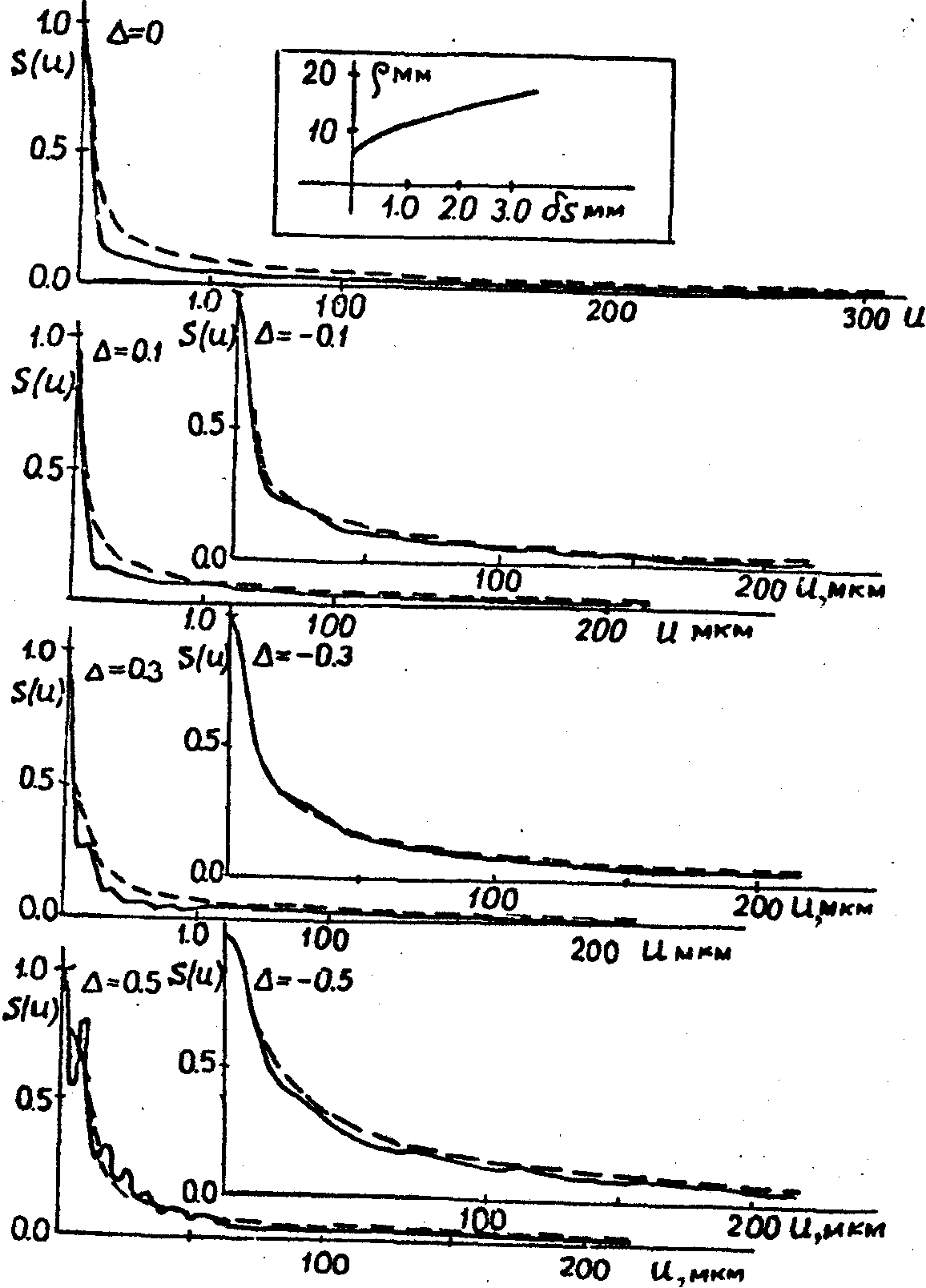
Рис.2. Распределения интенсивности в изображении линии при когерентном (сплошные кривые) и некогерентном (пунктирные) освещении для разных дефокусировок D
(мм) В рамке - график сферической аберрации объектива.
- 171 -
представлены на рве. 2. Как видно, в отличие от дифракционно ограниченного объектива, дефокусировка в разные стороны от плоскости D
= 0 приводит к нарушению симметрии sК(u) и sh(u). Структура sk(u) при положительных D
объясняется интерференцией пучков, проходящих различные участки апертуры объектива и испытывающие при этом неодинаковые фазовые искажения. Для положительных D
наблюдается структура и в sh(u). Однако, она менее выражена. Связано это с различием взаимодействия пучков в плоскости наблюдения при когерентном и некогерентном освещении. При некогерентном освещении sh(u) является результатом сложения интенсивности пучков, приходящих в точку наблюдения; при когерентном - происходит интерференция этих пучков. Этим и объясняются различия в sk(u) и sh(u). Случай отрицательных D
соответствует наблюдению sК(u) и sh(u) в плоскостях, в которых пучки, прошедшие различные участки апертуры объектива, не пересекаются. Вследствие этого структура sК(u) и sН(u) слабо выражена.
Перейдем к результатам исследований модуля h(u) и фазы j
(u) АФРЛ объектива для апертуры 0,06 рад. На рис.3 представлены половины симметричных значений h(u) и j
(u). Для D
= 0 вблизи точки u = 0 h(u) имеет резкий максимум. С увеличением u появляются монотонно убывающие "крылья", распространяющиеся до u = 310 мкм. Фаза j
(u) с ростом u монотонно убывает. Смещение плоскости наблюдения в область отрицательных D
приводит к размытию максимума h(u) и росту величины "крыльев" для всех u. В фазе АФРЛ также наблюдаются изменения. С ростом u её величина растёт. Особенно заметен рост j
(u) для больших u.
В случае положительных D
изменения h(u) и j
(u) носят другой характер. Для D
=0,05 изменения h(u) и j
(u) по отношению к D
= 0 незначительны. Для D
=+0,1 рядом с главным начинает появляться вторичный максимум. С дальнейшим ростом D
вторичная структура h(u) проявляется сильнее. Так. Для D
=0,3 и 0,5мм наблюдается уже 3 и 6 вторичных максимумов, соответственно. О природе их появления говорилось при сопоставлении sk(u) и sh(u).
- 172 -
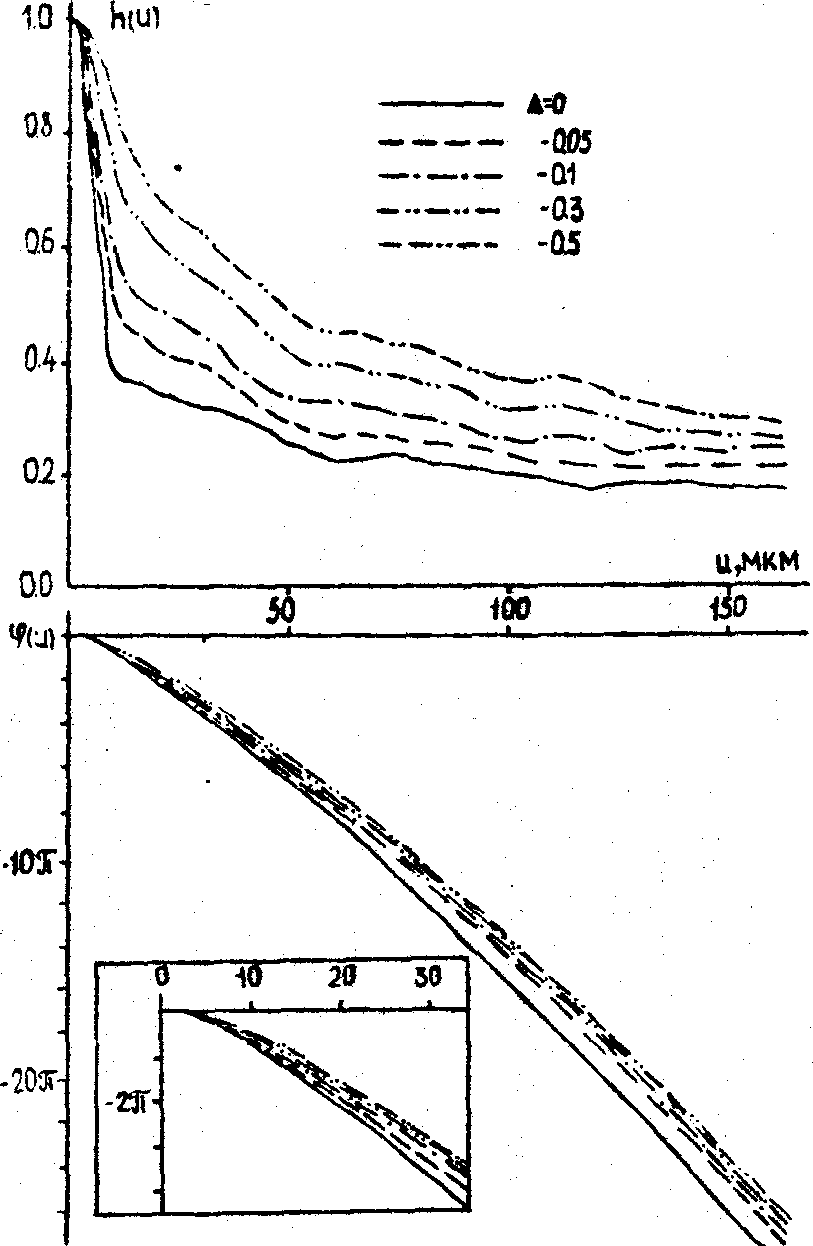 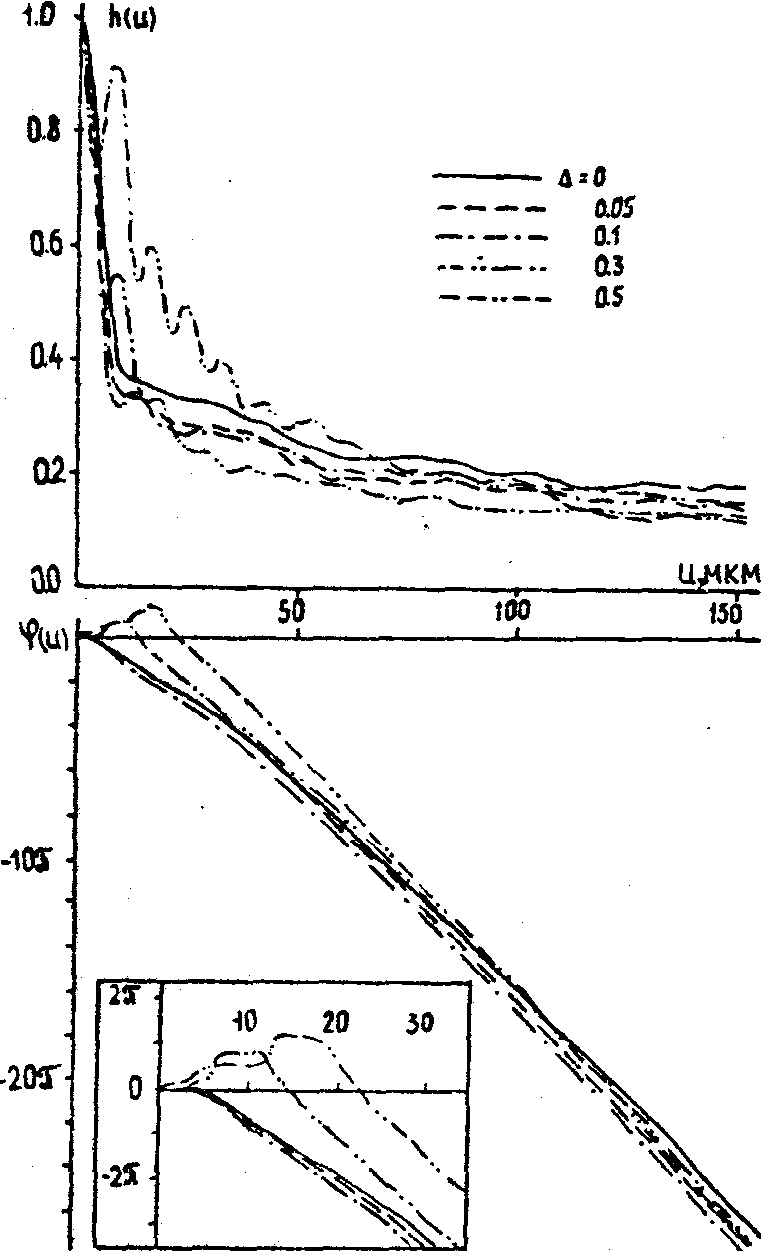
Рис.3. Распределение модуля h(u) и фазы j
(u) АФРЛ объектива для разных дефокусировок D
(мм).
- 173 -
фаза для указанных D
ведет себя сложным образом. Так, для D
=0,3 мм j
(u) в пределах главного максимума постоянна, а затем, в пределах вторичного максимума, наблюдаются положительные значения j
(u). С дальнейшим ростом u j
(u) начинает убывать. Для D
= 0,5 мм наблюдается еще большая структура j
(u). Растут размер области по u, в которой j
(u) положительна, изменения в j
(u) в положительную сторону. Вследствие сильной зависимости h(u) и j
(u) от D
, при формировании изображения устанавливается в плоскость фокусировки с возможно большей точностью.
При исследовании КПХ систем, включающих мутные среда, определение КПХ описанным в /10/ методом затрудняется значительным ослаблением светового потока, проходящего через систему. Эту трудность можно обойти, применяя голографическую запись прошедшего систему пучка с помощью пространственно когерентного референтного пучка. Как известно /14/, при равенстве ФВИ референтных пучков на этапах записи и восстановления голограммы для мнимого изображения восстанавливается пучок. ФВИ которого с точностью до постоянной совпадает с ФВИ объектного пучка. Для действительного изображения ФВИ восстановленного и объектного пучков с точностью до постоянной комплексно сопряжены. Обозначая через Гb(р1,р2), Г0(р1,р2) ФВИ восстановленного и объектного пучков в точках р1 и р2 плоскости голограммы, соответственно, для мнимого и действительного изображения, можно записать:
Г b(p 1,p 2) = const· Г0(р1,р2), Гb(p 1,p 2) = const· Г*0(р1,р2) (3)
С ФВИ референтного пучка на этапе восстановления Гr(p 1,p 2) и амплитудным пропусканием ta(рi) в точке р1,р2 Гb(р1, р2) связано соотношением /11/:
Г b(p 1,p 2) = Гr(p 1,p 2)t a(p 1)t *a(p 2) (4)
- 174 -
Степень когерентности восстановленного пучка m
b(p 1,p 2) найдем из (4), представляя Гr(р1,р2) как произведение корней квадратных из интенсивностей ir(р1) и i(p2) на степень когерентности m
r(р1,р2). Тогда получаем;
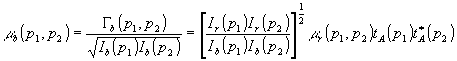
Учитывая, что ib(р1) = i r(р1)t a(p 1)t *a(p 1), a i b(p 2) = i r(p 2)t a(p 2)t *a(p 2), имеем
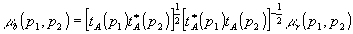 (5) (5)
при постоянной по сечению интенсивности референтного пучка а линейной записи ta(рi) голограммы пропорционально действующей экспозиции /15/, с учетом (3) и (4) для мнимого изображения вместо (5) получим
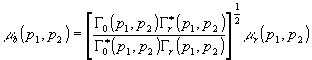
Используя соотношение Г (p1,p2) = 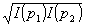 |
m
(p1,p2)|
exp[ij
(p1,p2)], где j
(p1,p2) - аргумент степени когерентности, после упрощения получим |
m
(p1,p2)|
exp[ij
(p1,p2)], где j
(p1,p2) - аргумент степени когерентности, после упрощения получим
m
b(p1,p2) = exp{i[j
0(p1,p2) - j
r(p1,p2)]} (6)
Окончательно для мнимого изображения из (6) будем иметь
|
m
b(p1,p2)|
= |
m
r(p1,p2)|
, j
b(p1,p2) = j
0(p1,p2)
В случае действительного изображения можно получить аналогично
|
m
b(p1,p2)|
= |
m
r(p1,p2)|
, j
b(p1,p2) = -j
0(p1,p2)
Таким образом, как для мнимого, так и действительного голографического изображений модуль степени пространственной когерентности непосредственно за голограммой совпадает с модулем степени когерентности референтного пучка на стадии восстановления. Если восстанавливать
- 175 -
голограмму полностью когерентным пучком (|
m
r(p1,р2) |
= 1 для произвольных р1, р2), то тогда модуль степени когерентности для всех точек пятна размытия линии в плоскости восстановленного изображения также будет равен 1 /16/. В связи с этим, при определении h(u), согласно (1), достаточно ограничиться измерением распределения интенсивности в восстановленном из голограмм изображении линии. Измерения j
(u) проводятся описанным выше образом, по сдвигу интерференционных полос.
Литература
1. Дж.Гудмен. Введение в Фурье-оптику. М., "Мир", 364 с., 1970.
2. М.Я.Шульман. Измерение передаточных функций оптических систем. М., "Машиностроение", 208 с., 1980.
3. Ю.В.Коломийцов. Интерферометры. Основы инженерной теории, применение. Л., "Машиностроение", 296с., 1976.
4. К.Престон. Когерентные оптические вычислительные машина. М., "Мир", 400 с., 1974.
5. В.П.Линник. Доклады АН СССР. № 5, 208-211, 1933.
6. Н.К.Бергер, И.А.Дерюгин, a.b.Миxeeнкo. Приборы в техника эксперимента, № 1, 197-198, 1978.
7. m.quantanilla, s.mar, i.arias. atti della "fondazlon giorgio ronchi", 33, n2, 206-218, 1978.
8. m.may. optica acta 16, n 5, 569-577, 1969.
9. v.j.tiziani, a.h.aemmer. optik, 36, n4, 443-453, 1972.
10. К.Г.Предко, В.Г.Синченко. В кн.: Физические основы голографии (Материалы xi Всесоюзной школы по голографии). Л., 130-136, 1979.
11. М.Борн, Э.Вольф. Основы оптики. М., "Наука", 720 с., 1973.
12. r.roler, r.krusche, r.van der heydt. optlk, 29, 30-44. 1969.
13. В.Я.Герловин. Оптика и спектроскопия, 39, вып.4, 759-764, 1975.
1 4. И.А.Дерюгин. В кн.: Материалы viii Всесоюзной школы по голографии, Л., 7-45, 1976.
15. Х.Фризер. Фотографическая регистрация информация. М., "Мир", 672 с., 1980.
16. b.j.thompson, c.roychodhuri. optica Аctа, 26, n1, 21-34, 1979.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

