|
|
 |
 |

|
| |
ТЕОРИЯ ВОССТАНОВЛЕНИЯ ОБЪЕМНЫХ ГОЛОГРАММ СПЕКЛ-ПОЛЕЙ
Б.Я.Зельдович, В.В.Шкунов
Рассмотрена задача дифракции света в объемной голограмме, записанной спекл-полем. Проведен количественный расчет эффектов, к которым приводит пространственный резонанс спекл-поля с неоднородностями среды, воспроизводящими профиль интенсивности записывающего поля. Показано, что внесение в записывающие пути спекл-структуры приводит для фазовых голограмм лишь к малому сдвигу кривой спектрально-угловой селективности при сохранении ее формы, а для голограмм с амплитудной компонентой в решетке ещё и к изменении величины максимума этой кривой.
Интерес голографистов к объемным средам постоянно поддерживается благодаря таким заманчивым свойствам объемных голограмм, как высокая дифракционная эффективность, наличие селективности по частоте и по углу, потенциально низкий уровень шумов и, тем самым, высокая информационная ёмкость на единицу площади /1/. В настоящее время технические трудности, связанные с созданием и обработкой фоточувствительных слоев большой голограммы успешно преодолеваются, о чём свидетельствуют, в частности, результаты с фотопластинками ПЭ-2 /2/ и освоение нового материала "реоксан" /3/. Такой прогресс стимулирует и теоретические исследования.
От теоретика, пытавшегося описать процесс восстановления объемной голограммы, требуется решить электродинамическую задачу дифракции считывающей опорной волны в среде фотослоя с сильными нерегулярными неоднородностями диэлектрической проницаемости e
( ) по всем трем пространственным координатам ) по всем трем пространственным координатам  : :
e
( ) = e
+ b
1(|
a(r)|
2 + |
b|
2 + b
2(ab*exp[i( ) = e
+ b
1(|
a(r)|
2 + |
b|
2 + b
2(ab*exp[i(  a - a -  b) b) ] + ] + к.с.) (1)
- 105 -
Здесь e
- однородная часть проницаемости , не затронутая экспозицией,
Ве xp[-iw
0t + i b b ] - поле опорной волны, a a( ] - поле опорной волны, a a( exp[iw
0t + i exp[iw
0t + i a a ] - поле объектной волны при записи, ] - поле объектной волны при записи,  А А и  В В - волновые векторы этих волн, b
1 и b
2 характеризуют светочувствительность среды на низких и высоких пространственных частотах, соответственно.
Благоприятным обстоятельством в этой неприступной, на первый взгляд, задаче является то, что неоднородности имеют в основном периодический характер, воспроизводя интерференционную решетку объектной и опорной волн АВ *еxp[i( a- a- b) b) ] + к.с. Однако, поскольку голограмма призвана регистрировать поля, несущие информацию в виде неоднородностей своей пространственной структуры, в наиболее интересном общем случае медленная амплитуда a( ] + к.с. Однако, поскольку голограмма призвана регистрировать поля, несущие информацию в виде неоднородностей своей пространственной структуры, в наиболее интересном общем случае медленная амплитуда a( ), а часто и b( ), а часто и b( ), оказываются функциями пространственных координат ), оказываются функциями пространственных координат  . В результате амплитуда и аза топографической решетки неоднородны как поперек голограммы, так и по глубине. Кроме того, на решетку накладываются крупномасштабные интрамодуляционные оптические неоднородности b
1 . В результате амплитуда и аза топографической решетки неоднородны как поперек голограммы, так и по глубине. Кроме того, на решетку накладываются крупномасштабные интрамодуляционные оптические неоднородности b
1( |
a(  ) |
2+ |
b(  ) |
2) . воспроизводящие профиль интенсивности каждого из полей.
Тем не менее, в настоящее время найдены и широко применяются несколько приближенных методов для решения теоретической задачи восстановления. Первый из них отвечает случаю малой эффективности голограммы и содержатся в пионерской работе Денисюка /4/. Ограничение малой эффективностью позволяет пренебречь истощением считывающей опорной волны 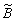 exp[-iw
t + i exp[-iw
t + i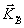  ], .т.е. воспользоваться Борновским приближением теории дифракции ], .т.е. воспользоваться Борновским приближением теории дифракции
e воост~b
2ab*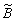 exp[-iw
t + i( exp[-iw
t + i( a+ a+ b+ b+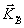 )]. Уже в этом приближении можно получить вид кривых спектрально-угловой селективности, оценить величину дифракционной эффективности в оптимальных условиях и вычислить уровень интрамодуляционных искажений восстановленного поля. )]. Уже в этом приближении можно получить вид кривых спектрально-угловой селективности, оценить величину дифракционной эффективности в оптимальных условиях и вычислить уровень интрамодуляционных искажений восстановленного поля.
Продвинуться теоретически в область больших дифракционных эффективностей удалось Кочельнику /5/ в модели плоских связанных волн, пожертвовав пространственной структурой записывающих полей. Несмотря на жесткое ограничение типа записывающих полей - плоские волны - этот подход обладает большой общностью. Так, для
- 106 -
голографических слоев не слишком большой, толщины, когда амплитуду голографической решетки можно считать постоянной по глубине голограмма, локально можно принять взаимодействующие волны плоскими, даже если в масштабах всей поверхности голограммы опорный и объектный пучки пространственно неоднородны. Программа вычисления вида восстановленного поля и уровня шумов в таких голограммах, которые мы называем толстослойными /9/, локальным применением теории плоских связанных волн проведена для гладких пучков гауссовского типа в /6,7/, а для пучков со слекл-структурой в /8,9/.
Наиболее сложным .для теоретического анализа оказался интересующий нас в этой статье случай собственно объемных голограмм, характеризуемых условием неоднородности голографической решетки не только поперек, но и по глубине /9/. Наиболее часто применяемый здесь метод состоит в разбиении волны объекта на отдельные плоские компоненты. Первый успех в расчетах режима высокой эффективности этим методом достигнут в работе /10/, в которой предполагалось, что каждая из компонент поля объекта дифрагирует лишь на своей голографической решетке, а интрамодуляционные слагаемые не учитывались. Расчет параксиальной фазовой просветной голограммы методом разложения по плоским волнам с учетом интрамодуляционных слагаемых проведен Сидоровичем в /11/. Потом появились работы для отражательных голограмм /12-15/ и ряд дротах /!6-23/ объединяемых общим названием "медовая теория" и выполненных в тех же терминах разложения по плоским волнам с предположением статистической независимости их амплитуд.
Следует отметить, что на языке пространственных структур такое предположение означает, что объектное поле в каждой точке образуется сложением малых независимых вкладов от разных точек объекта, т.е. обладает сильными пространственными неоднородностями типа спекл-структуры. Именно спекл-поля создают объемные голограммы, поскольку голографируемые поля без спекл-структуры обладают обычно масштабом продольной неоднородности заметно большим толщины фотослоя и хорошо описываются в модели толстослойных или гонких голограмм.
Пожалуй, в наиболее общем виде - для произвольной геометрии записи и произвольного типа голограммы и записывающих полей - выражения
- 107 -
для дифракционной эффективности объемной голограммы спекл-полей в зависимости от целого ряда параметров получены в работе /24/, в /25/ проведен расчет уровня шумов объемных голограмм, в /26/ - эффективности голограмм с наложенной записью, в /27/ - влияния нелинейности фотопроцесса на эффективность восстановления объемной голограммы.
Итак, в теории объёмных голограмм накоплен к настоящему времени довольно обширный материал, касающийся практически всех сторон проблемы. Однако, частично, видимо, из-за увлеченности мате -магической стороной сложной задачи, а частично из-за не всегда удачно выбираемых терминов и обозначений, теория использует большое число промежуточных параметров, не влияющих на конечный ответ (например, амплитуды компонент разложения), а её результаты представлены в виде довольно громоздких формул, трудных для непосредственного использования.
В настоящей работе мы попытаемся сформулировать теорию вое -становления объемных голограмм спекл-полей, опираясь, в частности, на процитированные работы /10-27/, в простой модели связанных волн, использующей минимальное число параметров. Задачей теории этого уровня, на наш взгляд, является расчет кривых спектрально-угловой селективности, т.е. их формы, характерной ширины и значений эффективности в максимуме. Чтобы представить результаты в терминах наблюдаемых величин, мы выбрали путь сравнения голограмм спекл-полей с голограммами плоских волн, свойства которых широко известны /5/.
Спеклон
При решении сложной математической задачи подчас полезно привлечь дополнительные физические соображения. Попробуем угадать вид решения в нашем случае. Пусть идеальная объемная голограмма записана плоской опорной родной be xp[i b b ] и несущей информацию спекл-волной объекта А( ] и несущей информацию спекл-волной объекта А( )exp[i )exp[i a a ], рис.1а. Требование идеальности голограммы означает, что при её восстановления опорной волной Веxp[i ], рис.1а. Требование идеальности голограммы означает, что при её восстановления опорной волной Веxp[i b b ] прошедшее через голограмму излучение содержит только восстановленное без искажений поле объекта А( ] прошедшее через голограмму излучение содержит только восстановленное без искажений поле объекта А( )еxp[i )еxp[i a a ] ]
- 108 -
и, возможно, остатки поля опорной полни, рис.1б. Если мы мысленно уберём заднюю часть фотослоя, уменьшив толщину голограммы, скажем, вдвое, то в отсутствие механических повреждений и в этом случае нет оснований ожидать появления искажений восстановленного поля объекта. Интенсивность в выходном поле лишь перераспределится в пользу остатка опорной волны за счет неполного ее перерассеяния в волну объекта, рис.1в.
Мысленную процедуру обрезания фотослоя можно повторить для наглядности еще много раз, однако и без этого понятно, что в сильно неоднородной среде идеальной объемной голограммы при восстановлении поле состоит из двух частей - опорной и объектной волн, причем пространственная структура обеих частой такая же, как у полей при записи, а сами волны связаны взаимным перерассеянием на решетке так, что их относительный вес по глубине голограммы меняется. Таким образом, мы опять приходя к идее связанных волн, но не только плоских, а обладающих спекл-структурой.
Чтобы найти приближение, в котором решение волнового уравнения в среде с диэлектрической проницаемость (1) имеет указанный вид, нам придется воспользоваться новым понятием, выкристаллизовавшимся в теории обращения волнового фронта при вынужденном рассеянии /28-33/ и получавшем права гражданства с публикацией обзора /34/ по этой теме. Обратимся к модельной ситуации. Пусть в светочувствительной среде тем или иным способом записана интерференционная картина только спекл-поля объекта a(  ):e
= e
0 + b
1|
a( ):e
= e
0 + b
1|
a( )|
2. Характерные масштабы получившихся неоднородностей определяются нерегулярной расходимостью спекл-поля D
q
А и составляют D
zn~l
/D
q
2a вдоль направления распространения поля и D
r^
~l
/D
q
a поперёк; здесь l
- длина волны излучения. Посмотрим, как распространяется в такой среде спекл-волна с пространственной структурой e( )|
2. Характерные масштабы получившихся неоднородностей определяются нерегулярной расходимостью спекл-поля D
q
А и составляют D
zn~l
/D
q
2a вдоль направления распространения поля и D
r^
~l
/D
q
a поперёк; здесь l
- длина волны излучения. Посмотрим, как распространяется в такой среде спекл-волна с пространственной структурой e( )~a( )~a( ), отвечающей записавшему неоднородности полю. ), отвечающей записавшему неоднородности полю.
Если оптическая сила неоднородности невелика, т.е. уровень искажений поля на каждой из них кd
e
D
z|
|
<< 1 мал, то на длине нескольких неоднородностей искажениями этого типа можно пренебречь и считать, что спекл-волна дифрагирует как в однородной, среде, так что структура распространяющегося поля находится
- 109 -
а)
б)
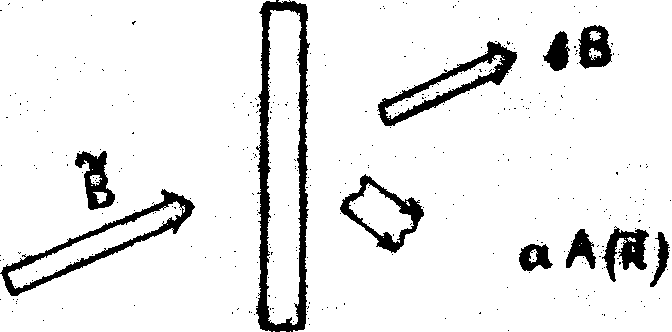
в)
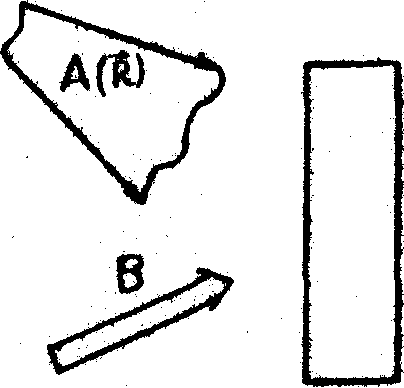
Рис.1. а) Схема записи голограммы плоской опорной волной В и спекл-волной объекта А(Р).
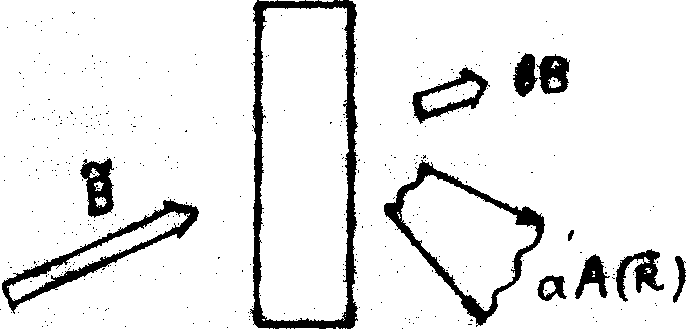
б) Восстановление голограммы полной толщины 1 волной В.
в) Восстановление голограммы с фотослоем половинной толщины 1/2.
- 110 -
в пространственном резонансе с неоднородностями - максимумы поля А(  ) приходятся на максимумы неоднородностей d
e
( ) приходятся на максимумы неоднородностей d
e
( )=b
1|
А( )=b
1|
А( )|
2, рис.3а. В результате большая часть потока энергии считывающей волны распространяется по местам с большей оптической плотностью (при b
1 > 0) и эффективная диэлектрическая проницаемость для согласованного поля Е( )|
2, рис.3а. В результате большая часть потока энергии считывающей волны распространяется по местам с большей оптической плотностью (при b
1 > 0) и эффективная диэлектрическая проницаемость для согласованного поля Е( )~a( )~a( ) должна быть выше, чем среднее по пространству значение. Можно ввести эффективную проницаемость определением ) должна быть выше, чем среднее по пространству значение. Можно ввести эффективную проницаемость определением
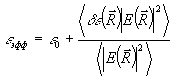
где угловые скобки означают усреднение по пространству, что для спекл-полей эквивалентно усреднению по ансамблю реализации. Тогда, поскольку спекл-поле обладает гауссовской статистикой, для согласованной конфигурации e(  )~a( )~a( ) получим e
эфф = e
0 + 2b
1<|
А|2>, т.е. добавка к проницаемости из-за экспозиции вдвое выше, чем средняя величина b
1 ) получим e
эфф = e
0 + 2b
1<|
А|2>, т.е. добавка к проницаемости из-за экспозиции вдвое выше, чем средняя величина b
1< |
a |
2>.
Для пространственного с неоднородностями поля <e(  )А* )А*(  )>=0, рис.2б, при условии малости неоднородностей кd
e
D
z|
|
<<1 среду в той же мере можно считать однородной, а её эффективную диэлектрическую проницаемость получить из того же определения e
эфф=e
0+b
1<|
a2|
>. Это соответствует среднему по пространству значений, что вполне естественно в отсутствие пространственного резонанса. Таким образом, эффективная диэлектрическая проницаемость среды с неоднородностями, записанными спекл-полем, зависит от вида распространяющегося по среде полю. )>=0, рис.2б, при условии малости неоднородностей кd
e
D
z|
|
<<1 среду в той же мере можно считать однородной, а её эффективную диэлектрическую проницаемость получить из того же определения e
эфф=e
0+b
1<|
a2|
>. Это соответствует среднему по пространству значений, что вполне естественно в отсутствие пространственного резонанса. Таким образом, эффективная диэлектрическая проницаемость среды с неоднородностями, записанными спекл-полем, зависит от вида распространяющегося по среде полю.
Хотя абсолютная величина отличия в эффективных проницаемостях обычно невелика D
e
»
10-4-10-6, его следствия для наблюдаемых величин могут быть весьма значительны. Так, если вариация проницаемости имеют отрицательную мнимую часть jmb
1 < 0, т.е. пространственно неоднородным является усиление как в случае вынужденного рассеяния стоксовой волны Е( ) в поле мощной волны накачки А( ) в поле мощной волны накачки А( ), пространственный резонанс согласованной конфигурации приводит к повышенное инкременту его усиления. Этот факт лежит в основе дискриминационного механизма выделения обращенной конфигураций из спонтанного шума при обращении волнового фронта в вынужденном рассеянии /28-34/. ), пространственный резонанс согласованной конфигурации приводит к повышенное инкременту его усиления. Этот факт лежит в основе дискриминационного механизма выделения обращенной конфигураций из спонтанного шума при обращении волнового фронта в вынужденном рассеянии /28-34/.
- 111 -
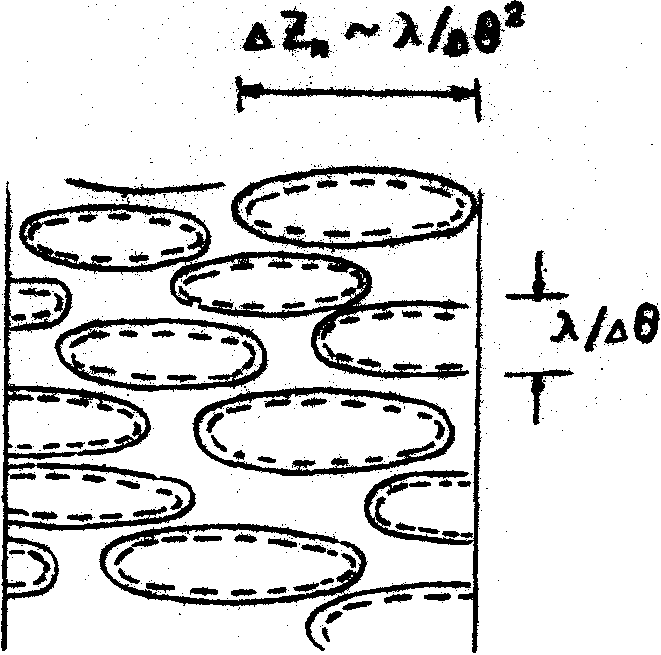
а)

б)
Рис.2. Иллюстрация пространственного резонанса спекл-структур поля (пунктирные линии) и неоднородностей среды (сплошные линии).
а) Наличие пространственного согласования - спеклон. б) Отсутствие пространственного согласования - некоррелированное решение.
- 112 -
Для чисто фазовых сред пространственный резонанс спекл-поля со спекл-неоднородностями меняет фазовую скорость волны, что может оказаться существенным в случае взаимного перерассеяния связанных волн. Для статических объемных голограмм, как будет видно из дальнейшего, поправка к фазовой скорости сдвигает условие Брэгга, а значит и положение максимума спектрально-угловой селективности. В динамическом случае такая поправка способна даже изменить направление перекачки энергии при самодифракции /35/.
Перейдем теперь от качественного обсуждения к уравнениям. Рассматриваемую в этом пункте модельную задачу можно решать в рамках параболического волнового уравнения для распространяющегося в направлении z поля Е( ): ):
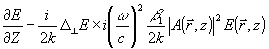 (2) (2)
Здесь k = w
/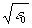  c - волновое число, c - волновое число, 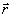 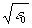  - поперечная координата, - поперечная координата, 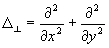 - поперечный лапласиан. Правая часть (2) описывает влияние наведенных интерференционной картиной спекл-поля А( - поперечный лапласиан. Правая часть (2) описывает влияние наведенных интерференционной картиной спекл-поля А( ) неоднородностей. ) неоднородностей.
Чтобы в рамках уравнения (2) получить решения, которые мы только что обсудили, следует поступить следующим образом: в правой части (2) выделить члены с пространственней зависимостью, удовлетворяющей левой части (2), т.е. параболическому уравнении для однородной среды:
|
a(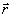 ,z)|
2e( ,z)|
2e(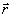 ,z) ®
<|
a|
2>e( ,z) ®
<|
a|
2>e(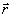 ,z) + <a*e>a( ,z) + <a*e>a(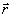 ,z) (3) ,z) (3)
а оставшимися членами (|А| 2Е - <|
a|
>2e - <a*Е>А) пренебречь. Получившееся уравнение действительно имеет два типа решений:
- коррелированное
ek(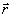 ,z) ~ a( ,z) ~ a(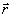 ,z)exp[2ic
1<|
a|
2>z] (4) ,z)exp[2ic
1<|
a|
2>z] (4)
и множество некоррелированных - <Е( 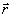 )А* )А*( 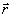 )> = 0,
ehk(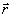 ,z) ~ e( ,z) ~ e(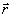 ,z)exp[ic
1<|
a|
2>z] ,z)exp[ic
1<|
a|
2>z]
- 113 -
где e(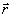 ,z) - решение уравнения (2) без правой части, c
1 ,z) - решение уравнения (2) без правой части, c
1= w
b
1/2c 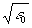 . Процедуру (3) в литературе вводили нескольким;: различными по форме и названиям, но эквивалентными математическими способами: выделение "автоматически брэгговских" членов при разложении полей по плоским волнам /11/, статическим усреднением /31/, выделением в поляризации среди эффективно возбуждающих левую часть слагаемых (2) /36/. Понятно, что суть не в названии и не в приговариваемых при выполнении преобразований словах. Следует количественно очертить область параметров, при которых учет отброшенных при замене (3) членов дает малые поправки. Основной параметр малости, позволяющий пренебречь такими поправками, уже упоминался выше kd
e
D
z|
|
<< 1 /37,29/. Более подробные исследования показали, что уровень этих поправок сильно зависит от соотношения действительной и мнимой частей коэффициента b
1, длины среды и ряда других параметров /32,25/. . Процедуру (3) в литературе вводили нескольким;: различными по форме и названиям, но эквивалентными математическими способами: выделение "автоматически брэгговских" членов при разложении полей по плоским волнам /11/, статическим усреднением /31/, выделением в поляризации среди эффективно возбуждающих левую часть слагаемых (2) /36/. Понятно, что суть не в названии и не в приговариваемых при выполнении преобразований словах. Следует количественно очертить область параметров, при которых учет отброшенных при замене (3) членов дает малые поправки. Основной параметр малости, позволяющий пренебречь такими поправками, уже упоминался выше kd
e
D
z|
|
<< 1 /37,29/. Более подробные исследования показали, что уровень этих поправок сильно зависит от соотношения действительной и мнимой частей коэффициента b
1, длины среды и ряда других параметров /32,25/.
В большинстве конкретных задач решение для коррелированной конфигурации заметно сложнее, чем в простой модельной ситуации (4). Самый общий вид решения Е k( 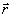 ,z)= ¦
( 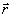 ,z)a( 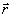 ,z) содержит зависящую от всех трех координат  огибающую ¦
( огибающую ¦
( ), которая является медленной функцией координат в масштабах спекл-структуры поля А( ), которая является медленной функцией координат в масштабах спекл-структуры поля А( ). Наличие такой огибающей с необходимостью сопровождается мелко-структурными искажениями, наконец, связь d
e
( ). Наличие такой огибающей с необходимостью сопровождается мелко-структурными искажениями, наконец, связь d
e
( ) с интенсивностью записывающего поля |a( ) с интенсивностью записывающего поля |a( )|2 может быть нелинейной в насыщающихся нелинейных средах или материалах с нелинейным фотооткликом. )|2 может быть нелинейной в насыщающихся нелинейных средах или материалах с нелинейным фотооткликом.
Тем не менее, в средах с неоднородностями, наведенными полем со спекл-структурой, пространственный резонанс согласованного поля и неоднородностей приводит к нетривиальным эффектам, и в подобных задачах именно согласованные к некоррелированные поля типа (4) и (5) являются адекватным базисом разложения искомого решения.
Термином спеклон мы решили назвать спекл-волну, согласованную со спекл-неоднородностями среды и резонансно с ними взаимодействующую. Кроме отсутствия аналогов в других областях физики и эвристических преимуществ, которые дает введение этого понятия в качестве базиса разложения для искомых полей в спекл-неоднородных
- 114 -
средах, у нас было еще одно основание придумать новое слово. Спеклон оказался удивительно устойчив к .изменению рада параметров - к спектральным /17,31/ и угловым /20,38,39/ сдвигам, а в ряде случаев и к уровню своего зашумления неоднородностями /32,34/. Последующее изложение является примером применения понятия спеклон для решения задачи дифракции спекл-полей при восстановлении объемной голограммы.
Дифракционная эффективность и спектрально-угловая селективность объемных голограмм
Рассмотрим процесс восстановления голограммы, которая записана плоской опорной волной Вe xp[i b b -iw
0t] и спекл-волной объекта a( -iw
0t] и спекл-волной объекта a( )exp[i )exp[i a a -iw
0t]. Примем следующие допущения: 1) считывающая опорная волна тоже является плоской; 2) все пучки одинаково поляризованы, так что можно ограничиться скалярной задачей; 3) голограмма является объемной, т.е. на её толщине укладывается много спекл-неоднородностей объектной волны, а небрегговскими максимумами дифракции можно пренебречь: -iw
0t]. Примем следующие допущения: 1) считывающая опорная волна тоже является плоской; 2) все пучки одинаково поляризованы, так что можно ограничиться скалярной задачей; 3) голограмма является объемной, т.е. на её толщине укладывается много спекл-неоднородностей объектной волны, а небрегговскими максимумами дифракции можно пренебречь:
l >> D
z|
|
~ l
/D
q
2a >> l
/q
2ab
q
ab - угол между записывающими пучками, D
q
a - спекл-расходимостъ волны объекта; 4) интрамодуляционные неоднородности d
e
a= b
1|
a(  ) |
2 являются слабыми, kd
e
aD
z |
|
>> 1 . Как видно из рассуждений предыдущего параграфа, решение для поля внутри голограммы в рамках таких допущений следует искать в виде
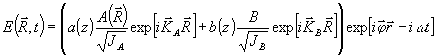 (6) (6)
Здесь средние интенсивности ja=<|
А|
2> и jb=|
b|
2, которые постоянны по площадке взаимодействия, введены для нормировки, a(z) и b(z) - искомые амплитудные веса двух связанных волн, z - координата в глубь голограммы, 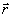 - в плоскости голограммы, вектор - в плоскости голограммы, вектор 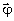 , лежащий в плоскости голограммы, учитывает возможное отличие частот и направлений опорных волн при считывании , лежащий в плоскости голограммы, учитывает возможное отличие частот и направлений опорных волн при считывании
- 115 -
и записи и необходим для удовлетворения граничным условиям на входной поверхности голограммы: 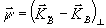 . Подставляя (6) в волновое уравнение для волны с частотой w
в среде с диалектической проницаемостью e
( . Подставляя (6) в волновое уравнение для волны с частотой w
в среде с диалектической проницаемостью e
( ), и (1) получим, пренебрегая небрэгговскими порядками дифракции и применяя правило (3) для учёта влияния интранеоднородпостей d
e
a ), и (1) получим, пренебрегая небрэгговскими порядками дифракции и применяя правило (3) для учёта влияния интранеоднородпостей d
e
a= b
1|
А( )|
2, систем уравнений для связанных волн: )|
2, систем уравнений для связанных волн:
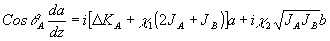 (7) (7)
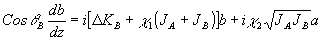 (8) (8)
где q
А,В - утлы между векторами  a,В a,В и осью z, нормалъной к поверхности голограммы, 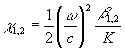 , D
КА и D
КВ - отличия волновых чисел при записи и восстановлении, вызванные изменением средней оптической плотности среды D
e
=e
¾
e
0 в результате обработки, отличием частот D
w
=w
-w
0 и направлений считывания, усадкой голограммы, r
=(l-l0)/l0. В первом порядке по этим параметрам можно получить /24/ , D
КА и D
КВ - отличия волновых чисел при записи и восстановлении, вызванные изменением средней оптической плотности среды D
e
=e
¾
e
0 в результате обработки, отличием частот D
w
=w
-w
0 и направлений считывания, усадкой голограммы, r
=(l-l0)/l0. В первом порядке по этим параметрам можно получить /24/
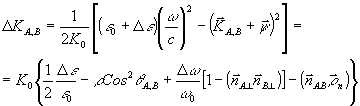 (9) (9)
Здесь 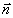 a,b - единичные орты в направлении распространения волн А и В, a,b - единичные орты в направлении распространения волн А и В, 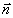 А^
,В^ А^
,В^
- их проекции на поверхность голограммы, d
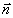 = = 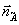 - -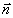 В В - векторный угол наклона опорной волны при считывании. Заметим, что при выводе (7), (8) и (9) мы не накладываем никаких ограничений на геометрию записи, в частности, плоскости падения пучков А и В могут не совпадать. Кроме того, здесь мы не отвлекаемся на исследование поляризационных свойств голограммы, поскольку они будут одинаковы для голограмм плоских волн и спекл-полей, а соответствующей формулы приведены в /24/. Отличие поляризаций в записываемых и считывающих полей очень легко учесть, модифицируя амплитуду кросс-решетки 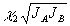 фактором | фактором |
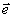 a a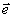 *b|
ps,p, где *b|
ps,p, где 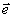 А,В А,В - произвольные комплексные
- 116 -
поляризационные орты записывающих волн, Р s=1 для s-поляризации, а Рр=cosq
a,b для р-поляризации восстанавливающей опорной волны.
Последние члены в правой части уравнений (7) и (8) описывают взаимное .пере рас сеяние волн на кросс-модуляционной решетке b
2АВ*exp[i(  a a-  b b)  ] +к.с., а члены, пропорциональные c
1 - влияние интрамодуляционных слагаемых b
1( |
a(  ) |
2+|b |
2). Как и следовало ожидать, влияние интрамодуляционных слагаемых в случае спекл-волны объекта А( ) различно для плосковолновой компоненты b(z)В и спеклона а(z)А( ) различно для плосковолновой компоненты b(z)В и спеклона а(z)А( ). Плосковолновая компонента некоррелирована с интрамодуляционными неоднородностями и воспринимает их среднее значение и её фазовый набег за счет экспозиции d
j
В~c
1(ja - jb), тогда как для спеклона из-за пространственного резонанса вес коррелированных неоднородностей выше. В нашем случае линейной записи d
e
~j( ). Плосковолновая компонента некоррелирована с интрамодуляционными неоднородностями и воспринимает их среднее значение и её фазовый набег за счет экспозиции d
j
В~c
1(ja - jb), тогда как для спеклона из-за пространственного резонанса вес коррелированных неоднородностей выше. В нашем случае линейной записи d
e
~j( ) пространственный резонанс удваивает силу воздействия и d
j
a ) пространственный резонанс удваивает силу воздействия и d
j
a~ c
1(2j a - j b). Таким образом, при низком уровне интрамодуляционных искажений система уравнений связанных волн (7), (8) в случае спекл-волны объекта a(r) отличается от соответствующей системы уравнений в случае двух плоских волн лишь добавочные членом ic
1jaa(z), описывающая пространственный резонанс спекл-поля с коррелированной частью неоднородностей.
Решение системы (7) и (8) в отсутствие поглощения при записи /16/ ja=const, jb=const трудностей не представляет /1,5,9-27/. Для дифракционной эффективности просветной голограммы cosq
a,b >0 имеем:
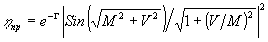 (10) (10)
Здесь сила голограммы М определяется,
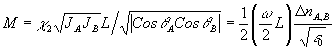 (11) (11)
средней амплитудой голографической решетки D
na,b=b
2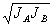 , параметр брэгговской отстройки , параметр брэгговской отстройки
v = v0 + ½c
1jal/cosq
a (12)
- 117 -
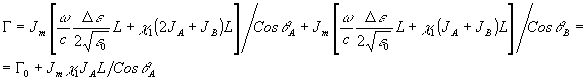 (13) (13)
где Г 0 отвечает случаю плоской волны объекта.
Параметры М и Г полностью задаются условиями записи и обработки голограммы. Изменение наклона и частоты считывающей опорной волны приводит к вариациям параметра брэгговской отстройки. Зависимость h
({rev) (10) с учетом (9) и (12) дает кривую спектрально-угловой селективности голограмма. Максимальная дифракционная эффективность для фазовых голограмм s in2m - достигается при считывании под углом Брэгга, т.е. при rev = 0. Ширина кривой спектрально-угловой селективности как для голограмм малой эффективности |
М|
<<1, так и для голограмм заметной силы |М|
~1 в единицах универсального параметра v составляет |rev|
£
p
.
Для отражательных голограмм имеем /1,59-27/:
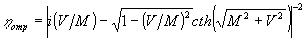 (14) (14)
где М и v даются как и раньше, формулами (11) и (12) с учетом того, что опорная волна встречная и Со sq
b<0, Соsq
a>0. Максимум эффективности для фазовых голограмм th2М - также достигается при строгом выполнении условия Брэгга rev=0. Ширина максимума в единицах v составит как и для просветных голограмм |
re|
£
p
при всех разумных значениях силы голограммы М.
Одинаковая ширина максимумов спектрально-угловой селективности в единицах re v отвечает различным ширинам единицах D
w
и D
q
В. Так, из (9) и (12) видно, что условие d
v£
p
отвечает для частотной селективности условию
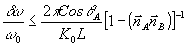
Для отражательных голограмм фактор 1-( 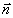 А А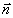 В В) всегда ~1¸
2 и их селективность высока. Для просветных голограмм селективность
- 118 -
будет сколь либо заметной только дня непараксиальных голограмм 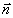 А ¹ А ¹
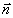 В. В.
Сравнение фазовых голограмм для плоских волн и для спекл-полей
Обсудим сначала чисто фазовые голограмма jmb
1,2= 0. Наличие или отсутствие спекл-структуры в объектном поле в этом случае приводит лишь к изменению чисто действительного параметра v. В результате, условие Брэгга максимально эффективного перерассеяния v=0 для голограмм плоских волн и спекл-полей, записанных и обработанных в идентичных условиях, выполняется при различных условиях считывания. Как видно из (10)-(14), внесение спекл-структуры в поле объекта приводит к сдвигу максимума кривой спектрально-угловой селективности. При этом максимальная дифракционная эффективность, ширина кривой и её форма при сохранена геометрии записи и средних интенсивностей записывающих пучков на голограмме остаются без изменений. Это, в частности, означает , что объемная голограмма в отличие от толстослойной, может дать 100%-ую дифракционную эффективность даже при записи спекл-полями. Направление сдвига максимума кривой определяется знаком величины b
1, а для угловой селективности ещё и геометрией запаси.
Сдвиг кривой селективности вызван тем, что из-за пространственного резонанса спеклона А с интранеоднородностями b
1|
А|
2 эффективный показатель преломления фоточувствительного слоя в процессе восстановления для спеклона и опорной волны оказывается различным - 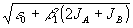 и и 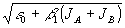 , соответственно. В результате радиусы сфер Эвальда /10,40/ для взаимодействующих волн не совпадают и волновые векторы этих волн при восстановлении удается замкнуть вектором решетки , соответственно. В результате радиусы сфер Эвальда /10,40/ для взаимодействующих волн не совпадают и волновые векторы этих волн при восстановлении удается замкнуть вектором решетки  А- А- В, изменив либо частоту, либо угол считывания, рис.3. В, изменив либо частоту, либо угол считывания, рис.3.
Величину самого сдвига легко оценить в единицах полуширины кривой селективности. По строгому критерию первого обращения в нуль (hwom) при малой эффективности голограммы М<<1 и приближенно при М ~ 1 полуширина определяется условием d
v(НwoМ)=p
.
- 119 -
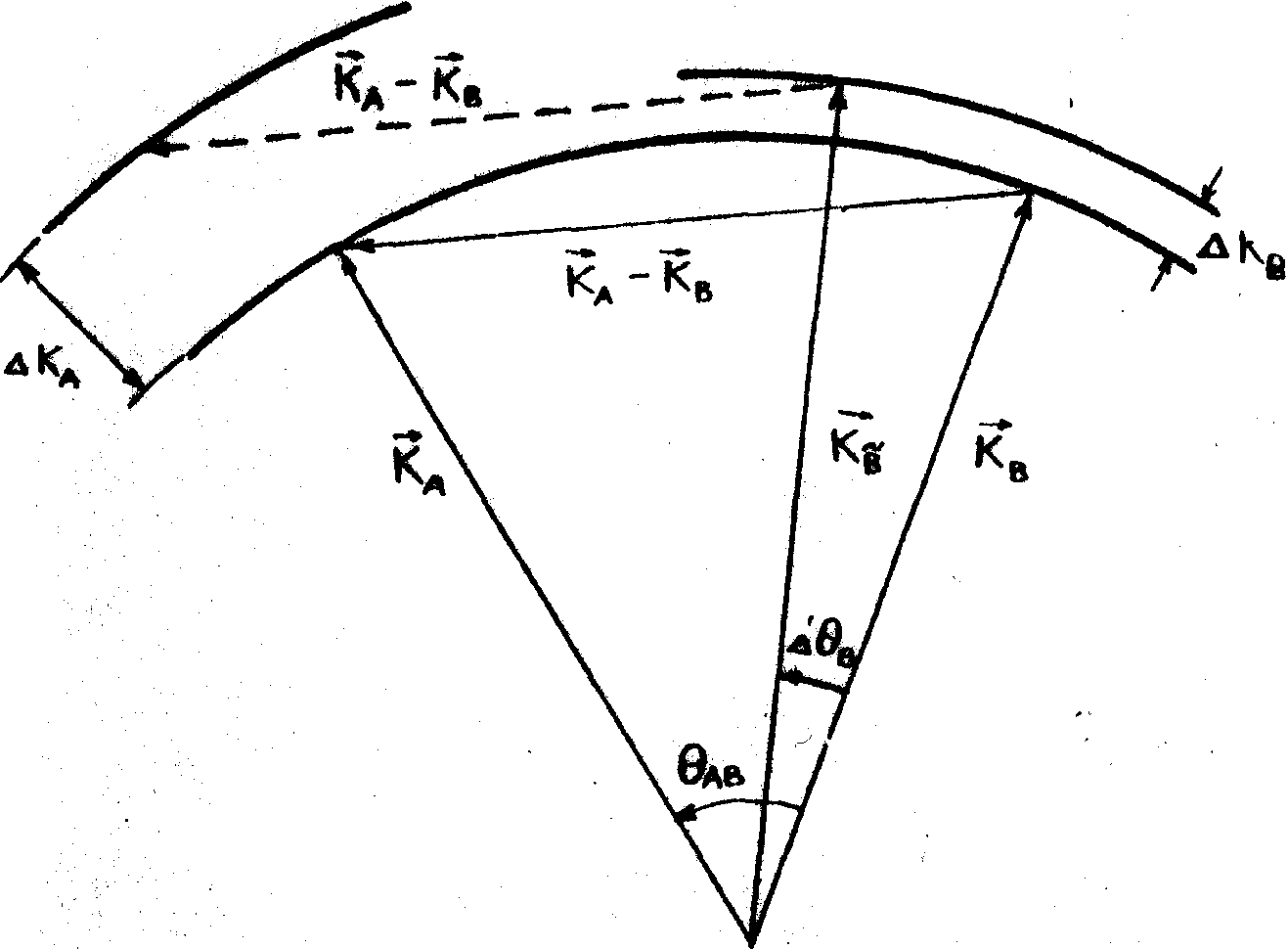
Рис.3. Из-за несовпадения радиусов сфер Эвальда считывающей опорной волны 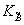 и спеклона и спеклона 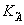 условие Брэгга дифракции на решетке с волновым вектором условие Брэгга дифракции на решетке с волновым вектором 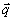 = = А¾ А¾
 В В удовлетворяется не для старого направления считывания 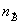 , а для нового , а для нового 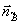 . .
- 120 -
Тогда, сдвиг кривой составит долю её полуширины:
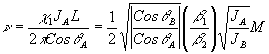 (15) (15)
Так, при ja=jb, b
1=b
2, cosq
a=Сosq
b сдвиг максимума составит М/2p
полуширины кривой селективности. В Борновском приближении М<<1 он составит 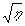 /2p
; в оптимальном режиме М = p
/2 - 1/4 полуширины. Таким образом, сдвиги весьма малы и процесс восстановления фазовой голограммы спекл-полей в типичной ситуации вполне удовлетворительно описывается в модели плоских волн. Выделим ситуации, когда, тем не менее, учет спекл-структуры записываемых полей оказывается существенным. /2p
; в оптимальном режиме М = p
/2 - 1/4 полуширины. Таким образом, сдвиги весьма малы и процесс восстановления фазовой голограммы спекл-полей в типичной ситуации вполне удовлетворительно описывается в модели плоских волн. Выделим ситуации, когда, тем не менее, учет спекл-структуры записываемых полей оказывается существенным.
Чисто формально сдвиги оказываются велики при
|
cosq
b|
>> |
cosq
a|
, ja >> jb, b
1 >> b
2
Из всех этих условий лишь последнее может реализоваться в практически интересных ситуациях по причине резкого максимума частотно-контрастной характеристики фотоматериала на низких пространственных частотах или несовпадения состояний поляризации волн А и В при записи.
Кроме этого, эффект может быть заметен для голограмм, практически не обладающих селектирующими свойствами. Так, при cosq
a=cosq
b просветная голограмма не имеет спектральной селективности, а при q
a,b << 1 практически не селектирует и по углу. В этом случае v0 = 0 при всех разумных частотах и направлениях считывания я внесение спекл-структуры в волну объекта природа при считывании к отклонению от оптимума, которое нельзя скомпенсировать частотно-угловыми сдвигами. Дифракционная эффективность при этом уменьшается, причем степень уменьшения зависит от соотношения интенсивностей записывающих волн /11/. Таким образом, для просветной голограммы без селективности спекл-структура в поле объекта может привести к вредному эффекту снижения дифракционной эффективности. Чтобы его избежать, следует лишь удовлетворить условию u
<<1, которое с хорошей точностью выполнено при 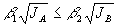 , т.е. когда интрамодуляционные неоднородности , т.е. когда интрамодуляционные неоднородности
- 121 -
не превышают амплитуду голографической решетки.
Амплитудные голограммы
Для чисто амплитудных голограмм r eb
= 0 сдвига кривой селективности не происходит, поскольку rev = rev0. Пространственный резонанс спекл-неоднородностей меняет в этом случае не фазовые скорости волн, а их темп поглощения или усиления: в голограммах с решетками коэффициента поглощения спеклон затухает на интранеоднородностях поглощения с вдвое большим инкрементом, а в усиливающих голограммах - нарастает с удвоенным инкрементом. В результате, внесение спекл-структуры в объектное поле голограмм коэффициента поглощения снижает их эффективность, а для голограмм коэффициента усиления, наоборот, её увеличивает. Количественно эти эффекты описываются формулами (10)-(14). Влияние спекл-структуры пренебрежимо как и для фазовых объемных голограмм при малом относительном весе интрамодуляционных неоднородностей. В общем случае амплитудно-фазовых регистрирующих сред могут присутствовать оба эффекта - сдвиг положения максимума кривой селективности и изменение его величины. В большинстве реальных ситуаций эти эффекты невелики.
Случай спекл-структуры в опорной волне
Полученные результаты нетрудно обобщить на случай, когда спекл-структуру несет и опорнаяволна В(  )еxp[i )еxp[i b b ]. Пространственный резонанс спеклона В( ]. Пространственный резонанс спеклона В( ) с интранеоднородностями b
1|
В( ) с интранеоднородностями b
1|
В( )|
2 приведёт к возникновению в правой части (8) дополнительною слагаемого ic
1jbb(z). В результате изменятся два из параметров, определяющих дифракционную эффективность просветных (10) и отражательных (14) голограмм: )|
2 приведёт к возникновению в правой части (8) дополнительною слагаемого ic
1jbb(z). В результате изменятся два из параметров, определяющих дифракционную эффективность просветных (10) и отражательных (14) голограмм:
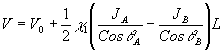 , , 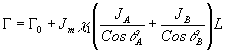
Если, как в случае голографической коррекции, объектная волна при этом будет плоской, соответствующие формулы примут вид:
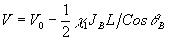 , , 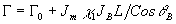
- 122 -
И в этих случаях влияние спекл-тструктуры (при малости шумов) сведётся к двум возможным эффектам. Для фазовых голограмм кривая селективности сдвигается, но на величину, отличную от случая плоской опорной волны, - большую для отражательных и меньшую для просветных голограмм. Для амплитудных голограмм появится также дополнительное затухание или усиление. Интересно отметить, что если обе записывающие волны несут спекл-структуру, при jacosq
b=jbcosq
a сдвигов максимума кривой не происходит.
3аключение
Резюмируем основные результаты. Показано, что внесение спекл-структуры в записываемые голограммой поля приводит для фазовых объемных голограмм к малому сдвигу кривой спектрально-угловой селективности, сохраняя значение эффективности в максимуме и форму кривой, а при наличии амплитудной составляющей решетки еще и к небольшому изменению максимальной эффективности. Проведен количественный расчет этих аффектов. Влияние спекл-неоднородностей заметно лишь при большом относительном весе интрамодуляционных возмущений диэлектрической проницаемости голограммы.
Все эти выводы справедливы для "идеальной" голограммы. т.е. в пренебрежении шумами. При заметном уровне интрамодуляционного шума отличия голограмм плоских волн и спекл-полей более существенны - интранеоднородности спекл-поля приводят к возникновению шумов. Количественно интрамодуляционные шумы объемных голограмм исследованы в /25/ хотя приведенные в этой работе вычисления довольно громоздки и, видимо, пришло время их ревизовать с позиций теории спеклонов, общий вид можно сформулировать следующий образом. Вполне доступен такой режим работы объёмной голограммы, когда дифракционная эффективность ~100%, а уровень интрамодуляционных шумов пренебрежимо мал, тогда как для толстослойных голограммы высокая эффективность автоматически означает высокий уровень шумов /9/. Этот вывод является лишним аргументом для стимулирования разработки голографических сред с глубокой записью, т.е. с толщиной фотослоя ~ 0,1 см.
- 133 -
Литература
1. Кольер Р., Беркхарт К., Лин Л. "Оптическая голография" - Мир, m., 1973.
2. Кириллов Н.И. "Высокоразрешающие фотоматериалы для голографии и процессов их обработки" - Наука, m., 1979.
3. Суханов В.И., Лашков Г.И. и др. В кн.: "Оптическая голография" - Наука, Л., 1979, стр.24.
4. Денисюк Ю.Н. Опт. спектр., 1963, 15, 522.
5. kogelnik h., bell.syat.techn.j., 1969, 48, 2909.
6. Сooke d.j., solymar l., sheppard c.j.r. int.j.electron., 1979, 46, 337.
7. Якимович А.П. Оптика и спектроскопия. 1979, 47, 960.
8. upatnieks j., leonard С., j.opt.soc.am., 1970, 60, 297.
9. Зельдович Б.Я., Даунов В.В., Яковлева Т. В. Квантовая электроника. 1983, 10, №7.
10. Аристов В.В., Шехтман В.Ш. УФН, 1971, 104, 51.
11. Сидорович Е.Г. ЖТФ, 1976, 46, 1306.
12. Зельдович Б.Я.. Шкунов В.В. Препринт ФИАН. 1978, № 266.
13. Лещев А.А., Сидорович b.Г. Опт.спектроск., 1978, 44, 302.
14. Зельдович Б.Я,, Шкунов В.В. Квантовая алектроиика, 1979. 6, 1533.
15. Лещёв А.А., Сидорович В.Г. В кн. "Оптическая голография", Наука, Л., 1979, стр.42.
16. Зельдович Б.Я, Шкунов В.В, Кр.сообщ.физ., 1979, стр.24, №1.
17. Сидорович В.Г., Шкунов В.В. Оптика и спектроскопия, 1978, 44, 1001.
18. shkunov v,v., zel'dovich b.ya., appl.opt., 1979, 18, 3633.
19. Зельдович Б.Я., Шкунов В.В. В сб. Физические основы голографии, Л., 1978, с.46-84.
20. Баранова Н.Б., Зельдович Б.Я., Шкунов В.В., Яковлева Т.В. В сб. Голография и оптическая обработка информации: методы и аппаратура". Л., 1980. с.3-38.
21. Сидорович В.Г. В сб. Голографические методы исследования. Л., 1978. с.161-186.
22. Краснов А.Е. Квантовая электроника, 1977, 4, 2011.
- 124 -
23. Краснов А.Е. Квантовая электроника, 1980, 7, 818.
24. Зельдович Б.Я., Шкунов В.В., Яковлева Т.В. Препринт ФИАН, 1979, № 54.
25. Зельдович Б.Я., Шкунов В.В., Яковлева Т.В. Препринт ФИАН, 1979, № 26.
26. Зельдович Б.Я., Шкунов В.В., Яковлева Т.В. В кн.: "Проблемы оптической голографии" - Наука, Л., 1981, с.80-97.
27. Зельдович Б.Я., Яковлева Т.В. Квантовая электроника, 1980, 7, 519.
28. Зельдович Б.Я., Поповичев В.И., Рагульский В.В., Файзуллов Ф.С. Письма в ЖЭТФ, 1972, 15, 160.
29. Сидорович В.Г. ЖТФ, 1976, 46, 2168.
30. Бельдюгин И.М., Галушкин М.Г., Земсков Е.М., Мандросов В.И. Квантовая электроника, 1976, 3, 2467.
31. Зельдович Б.Я., Шкунов В.В. Квантовая электроника, 1977, 4, 1090.
32. Зельдович Б.Я., Шкунов b.В. Квантовая электроника, 1978, 5, 36.
33. Зельдович Б.Я., Шкунов В.В. ЖЭТФ, 1978, 75, 428.
34. Зельдович Б.Я., Пилипецкий Н.Ф., Шкунов В.В. УФН, 1982, 138, 249.
З5. Духовный А.М., Стаселько Д.И., Письма ЖТФ, 1982, 8, 1009:
Суханов В.И., Корзинин В.Л. Письма ЖТФ, 1982, 8, 1144.
36. Беспалов В.И., Бетин А.А., Пасманик Г.А. Изв. ВУЗов, Радио-физика, 1978, 21, 961.
37. Бетин А.Л., Пасманик Г.А. Письма ЖЭТФ, 197 6, 23, 577.
38. Баранова Н.Б., Зельдович Б.Я. Квантовая электроника, 1980, 7, 299.
39. Баранова Н.Б., Зельдович Б.Я.. Квантовая электроника, 1980, 7, 973.
40. Эвальд П. УФН, 1966, 89, 287.
41. Мамаев А.В., Мухин Ю.В., Пилипецкий Н.Ф., Шкунов В.В. Квантовая электроника, 1983, 10, 1483.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

