ПРОЯВЛЕНИЕ ТОНКОЙ СТРУКТУРУ СЛЕКЛ-ПОЛЕЙ ПРИ ИХ ИНТЕРФЕРЕНЦИИ
И.С.Клименко, В.П.Рябухо, Б.В.Федулеев
Обсуждается эффект осцилляции интерференционных полос в голографической и спекл-интерферометрии, обусловленный конкретным наложением идентичных спекл-модулированных полей.
1. Введение
В последние годы заметный интерес вызывают вопросы, связанные с изучением световых полой, содержащих вследствие диффузного рассеяния, так называемые спекл-структуры. С такими световыми полями приходится сталкиваться в голографии и голографической интерферометрии /1-3/, при обращении волнового фронта /4,5/ в астрономии /6/ и в других задачах. Получило распространение новое направление интерференционных измерений, основанное на регистрации спекл-структур и именуемое спекл-интерферометрией /7,8/.
Есть основания считать (см. /9/), что методы голографической и спекл-интерферометрии базируются на обидах физических принципах интерференции диффузно рассеянных световых полей (спекл-полей). Такой подход позволяет рассматривать формирование голографических и спекл-интерферограмм с единых позиций, основанных на анализе взаимных смещений спекл-полей и учете роли зрачка оптической системы (играющего роль пространственного фильтра).
Интересные особенности .cnew-полей были выявлены в недавней работе /10/, в которой осуществлялось когерентное наложение исследуемого спекл-поля и однородного (опорного) поля.
- 71 -
В настоящей работе исследуется тонкая структура спекл-поля, связанная с характерным распределением комплексной амплитуды света в каждом его элементе (индивидуальном спекле) к проявляющаяся при когерентном наложении двух идентичных, но сдвинутых друг относительно друга спекл-полей. Интересно, что при этом появляется возможность наглядной визуализации функции поперечной когерентности спекл-поля.
Для получения двух взаимно-сдвинутых идентичных спекл-полей нами использовалась голографическая интерферометрия - регистрировалась двукратно экспонированная голограмма диффузно отражающего квазиплоского объекта, который в промежутке между экспозициями поворачивался на малый угол вокруг оси, близкой к нормали к его поверхности.
Выбор голографической интерферометрии в качестве средства суперпозиции спекл-полей обусловлен возможностью воспроизведения комплексной амплитуды световых полей, допускающей управление протяженностью и амплитудным распределением индивидуальных спеклов путем изменения апертуры на этапе восстановления, а выбор вращательного сдвига - обеспечением центральной симметрии и линейным приращением относительно смещения спеклов с удалением от оси вращения.
2. Смещение спекл-поля в плоскости изображения при вращении диффузно-рассеивающего объекта
Запишем1комплексную амплитуду светового поля, восстановленного двукратно экспонированной голограммой квазиплоского диффузно отражающего объекта в плоскости его изображения (см.рис.1, на
- 72 -
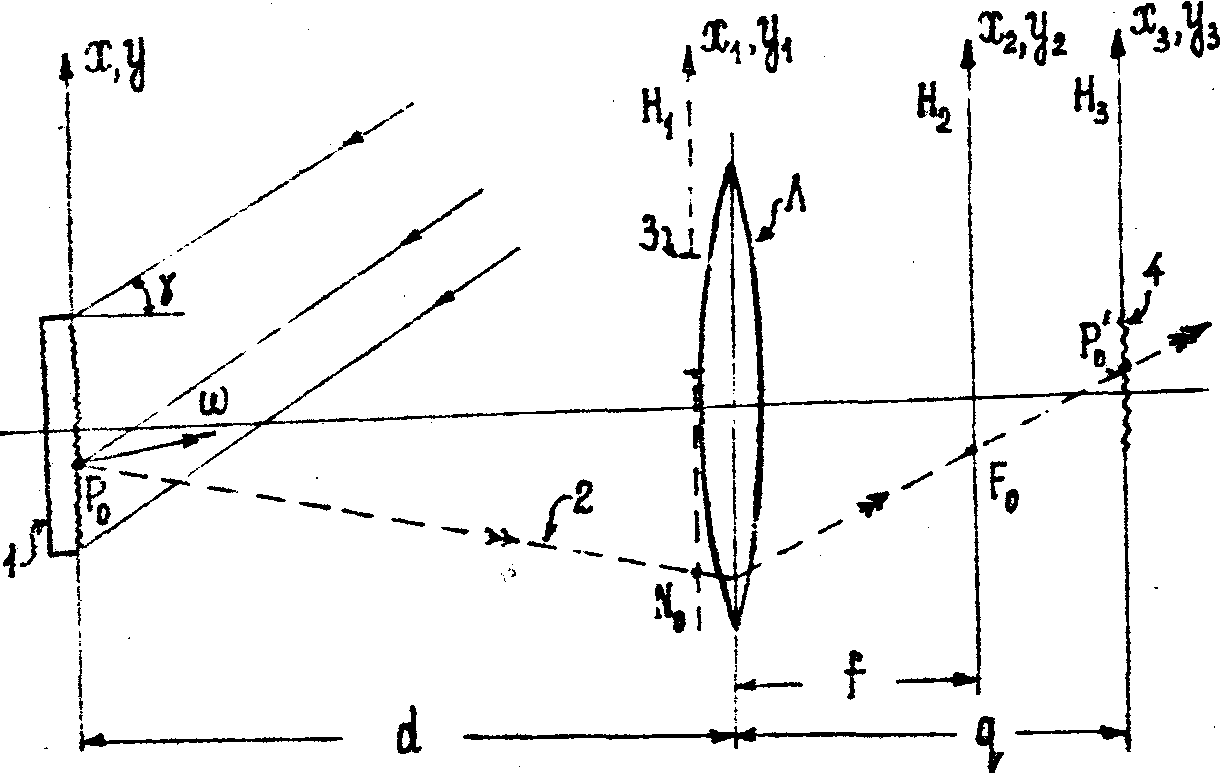
Рис.1. Формирование (восстановление) объектного светового поля. 1 - объект (восстановленное изображение), 2 - ось поворота, 3 - входной зрачок, 4 - действительное изображение, Л - линза, Н1, h2, Н3 - соответственно, плоскости входного зрачка, Фурье-, резкого изображения.
- 73 -
котором в целях упрощения голограмма и восстанавливающий пучок не показаны) в виде
u(x,y) = u1(x,y) + u2(x,y) = t(x,y)exp(i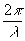 sing
x) + t(x + w
y,y - w
x)exp(i
sing
x) + t(x + w
y,y - w
x)exp(i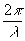 sing
x)(1)
sing
x)(1)
где l
- длина волны излучения, g
- угол освещения объекта, w
- угол поворота объекта, а функция t(х,у) имеет смысл комплексного коэффициента отражения объекта и может быть представлена как
t(x,y) = t0(x,y)exp[iФ(x,y)] (2)
Здесь t0(x,y) - является макроскопической характеристикой поверхности (амплитудный коэффициент отражения), а exр[iФ(x,у)] - микроскопической, представляющей изменяющееся случайным образом по поверхности объекта диффузное рассеяние.
Пусть восстановленное световое поле переотображается (рис.1) положительной линзой, которую считаем обобщенным представлением произвольной наблюдательной или регистрирующей системы глаз, фотоаппарат и т.п.). Тогда комплексную амплитуду в плоскости х3,у3, оптически сопряженной с плоскостью изображения объекта, для его исходного положения можно представить /11/ выражением;
u1(x3.y3) = cò
ò
t(x1,y1)p(x1,y1)exp[i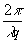 (x1x3 + y1y3)]dx1dy1
(x1x3 + y1y3)]dx1dy1
где 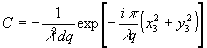 , d и q - расстояния от восстановленного изображения до линзы и от линзы до сформированного
, d и q - расстояния от восстановленного изображения до линзы и от линзы до сформированного
- 74 -
ею изображения, соответственно, р(х1,у1) – функция пропускания входного зрачка наблюдательной системы и
t(x1,y1) = ò
ò
t(x,y)exp(i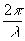 sing
x)exp[-
sing
x)exp[-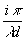 (x2 + y2)]exp[i
(x2 + y2)]exp[i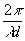 (xx1 + yy1)]dxdy (4)
(xx1 + yy1)]dxdy (4)
Выражение (4) с точностью до постоянного коэффициента и фазового множителя сферической волны представляет собой интеграл Френеля-Кирхгофа, записанный в приближении Френеля /12/, и описывает комплексную амплитуду объектного поля в плоскости входного зрачка.
В общем случае, когда ось вращения объекта, определяемая вектором w
(w
х,0,w
z), составляет некоторый угол с нормалью к поверхности объекта и пересекает её в произвольной точке p0(x0,y0), комплексную амплитуду для смещенного положения объекта можно представить в виде
|
u2(x3,y3) = cò
ò
exp[i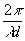 w
z(y0x1 – x0y1)]t(x1 - w
zy1 - w
zy0,y1 - w
zx1 - w
zdsing
+ w
z(y0x1 – x0y1)]t(x1 - w
zy1 - w
zy0,y1 - w
zx1 - w
zdsing
+ |
(5) |
|
+ w
zx0 + w
xdcosg
)p(x1,y1)exp[i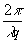 (x1x3 + y1y3)]dx1dy1 (x1x3 + y1y3)]dx1dy1 |
Следовательно, световые поля, соответствующие исходному и смещенному положениям объекта и имеющие, в силу диффузного рассеяния света микроструктурой объекта, сложный фазовый микрорельеф случайного характера, повернуты друг относительно друга на угол вокруг оси, проходящей через точки Р0 и n0(x10,y10) с координатам:
x10 = x0 - dsing
+ 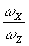 (1 + cosg
), y10 = y0, z = d (6)
(1 + cosg
), y10 = y0, z = d (6)
- 75 -
Уравнение этой оси (прямой) определяется соотношениями:
x1 = z[- sing
+ 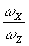 (1 + cosg
)] + x0, y1 = y0, (7)
(1 + cosg
)] + x0, y1 = y0, (7)
которые показывают, что ось вращения объекта и ось поворота объектного светового воля лежат в плоскости, компланарной направлению освещения объекта и направлению поворота, причем ось вращения объекта является биссектрисой угла между этими направлениями.
В плоскости резкого изображения, сформированного линзой, в предположении, что угловая апертура голограммы больше угловой апертуры линзы, комплексная амплитуда суперпозиционного поля равна сумме комплексных амплитуд, определяемых выражениями (3) и (5).
Пусть входном зрачок наблюдательной системы (линзы) имеет форму круглого отверстия радиуса r с центром в некоторой точке х1Р, у1Р. Функцию пропускания такого зрачка запишем в виде
p(x1,y1) = rect(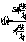 )Ä
d
(x1 – x1p,y1 – y1p) (8)
)Ä
d
(x1 – x1p,y1 – y1p) (8)
где Ä
знак операции свертки, d
(x1,y1) - дельта-функция,
В подавляющем большинстве случае при наблюдении голографических интерферограмм приходился использовать наблюдательные системы с сильно ограниченной апертурой (см., например, /3/), что позволяет получать интерференционные волосы высокого контраста. Поэтому вначале наложим ограничение на радиус отверстия входного зрачка, а именно, будем считать, что в пределах отверстия относительное смещение световых волн можно рассматривать как поступательное поперечное смещение, величина которого определяется положением центра входного зрачка. Кроме того, потребуем, чтобы в пределах отверстия входного зрачка изменения показателя функции
- 76 -
exр[i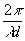 w
z(y0x1 – x0y1)], указывающей на изменение угла наклона объектного светового поля в результате поперечного смещения объекта на величину
w
z(y0x1 – x0y1)], указывающей на изменение угла наклона объектного светового поля в результате поперечного смещения объекта на величину 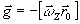 , где
, где 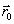 - радиус-вектор точки p0, были бы значительно меньше p
. Последнее накладывает ограничение,на положение точки Р0.
- радиус-вектор точки p0, были бы значительно меньше p
. Последнее накладывает ограничение,на положение точки Р0.
С учетом этих ограничений комплексную амплитуду в плоскости х3,у3 можно представить в виде
|
u(x3,y3) = cò
ò
t(x1,y1)p(x1,y1)exp[i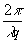 (x1x3 + y1y3)]dx1dy1 + (x1x3 + y1y3)]dx1dy1 + |
(9) |
|
+ cexp[i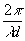 w
z(y0x1p + x0y1p)]ò
ò
t(x1 – a,y1 – b)b(x1,y1)exp[i w
z(y0x1p + x0y1p)]ò
ò
t(x1 – a,y1 – b)b(x1,y1)exp[i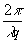 (x1x3 + y1y3)]dx1dy1 (x1x3 + y1y3)]dx1dy1 |
где а = -w
zy1p + w
zy0,
b = w
zx1p + w
zdsing
- w
xx0 + w
xd + w
xdcosg
.
Соотношение (9) представляет собой сумму интегралов Фурье от произведения двух функций - комплексной амплитуды света в плоскости входного зрачка и функции пропускания входного зрачка, причем смещенное поле в плоскости зрачка имеет поперечный сдвиг по отношению к исходному.
Пользуясь известными свойствами преобразования Фурье, выражение (9) можно привести к виду:
u(x3,y3) = d2l
2c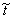 2(x3,y3)Ä
p(x3,y3){1 + exp[iy
(x3,y3)] (10)
2(x3,y3)Ä
p(x3,y3){1 + exp[iy
(x3,y3)] (10)
где
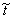 (x3,y3) = t(b
x3,b
y3)exp(i
(x3,y3) = t(b
x3,b
y3)exp(i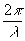 sing
b
x3)exp[i
sing
b
x3)exp[i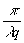 b
(x23 + y23)] (11)
b
(x23 + y23)] (11)
- 77 -
y
(x3,y3) = 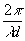 b
[w
z(y0x1p – x0y1p) – ax3 – by3] (12)
b
[w
z(y0x1p – x0y1p) – ax3 – by3] (12)
p(x3,y3) = f[p(x1,y1)] = ò
ò
p(x1,y1)exp[i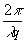 (x1x3 + y1y3)]dx1dy1 (13)
(x1x3 + y1y3)]dx1dy1 (13)
Здесь b
= -d/q - поперечное увеличение, f - операторный символ Фурье-преобразования.
При получении (10) мы вынесли из-под знака интеграла свертки функцию exp[iy
(x3,y3)] как медленно меняющуюся в силу малости величин w
Х и w
z, предполагая, что её период значительно больше области существования (ширины) функции p(х3,у3). Очевидно, что период экспоненты определяет период интерференционных волос, вызванных вращением объекта, тогда как ширина функции p(х3,у3) определяет характерный размер индивидуальных спеклов в плоскости изображения.
Выражение (11) описывает перевернутое изображение объекта с измененным в раз масштабом. Экспоненциальные фазовые множители плоской и сферической юли в нашем рассмотрении не играют существенной роли, так же как и фазовый множитель сферической волны, содержащийся в коэффициенте С.
Операцию свертки функции 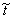 (х3,у3) с Фурье-образом функции пропускания входного зрачка. В силу диффузного рассеяния света поверхностью объекта, фаза световой волны в объектном поле меняется случайным образом от точки к точке, однако, при уширении каждой такой точки до Фурье-образа входного зрачка считается /13,14/, что фаза становится детермированной в пределах некоторой области, размеры и форма которой определяются параметрами
(х3,у3) с Фурье-образом функции пропускания входного зрачка. В силу диффузного рассеяния света поверхностью объекта, фаза световой волны в объектном поле меняется случайным образом от точки к точке, однако, при уширении каждой такой точки до Фурье-образа входного зрачка считается /13,14/, что фаза становится детермированной в пределах некоторой области, размеры и форма которой определяются параметрами
- 78 -
входного зрачка. Эту область и следует рассматривать как элементарную область пространственной когерентности диффузно рассеянного светового поля (спекл-поля), переотображенного оптической системой с некоторой функцией пропускания. Очевидно, что чем меньше размеры входного зрачка, тем шире функция p(х3,у3), т.е. тем больше область пространственной когерентности спекл-поля 1).
При выводе выражения (10) предполагалось, что функция p(х3,у3) имеет достаточную ширину за счет малых размеров зрачка. Это предположение соответствует пространственному перекрытию идентичных элементарных областей когерентности (спеклов) в световых полях, восстановленных двукратно экспонированной голограммой. В результате имеет место интерференция между участками волновых фронтов с одинаковой фазой, что эквивалентно представлению об интерференции идентичных (соответственных) точек /15/.
Наблюдаемое в плоскости изображения распределение интенсивности представим соотношением;
<i(x3,у3)> = 2b
2<|
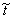 (x3,y3)Ä
p(x3,y3)|
2>{1 + cos[y
(x3,y3)] (14)
(x3,y3)Ä
p(x3,y3)|
2>{1 + cos[y
(x3,y3)] (14)
где введено усреднение по области пространства, для которой y
(x3,y3) = const, с целью исключения из рассмотрения спекл-модуляции интерферограммы, сформированной на фоне изображения объекта. Как следует из (12), интерферограмма, характеризующая поворот объекта, имеет вид прямолинейных эквидистантных полос с
1) Здесь речь идет об образовании при взаимном наложении спекл-полей "низкочастотной" интерференционной картины, период которой значительно превышает размер индивидуальных спеклов.
- 79 -
пространственными частотами во осям х3 и у3:
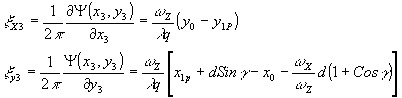 (15)
(15)
Отсюда видно, что пространственные частоты интерферограммы зависят от положения центра входного зрачка относительно точки n0(x10,у10), координаты которой определяются соотношением (6).
3. Закономерности локализации интерферограмм и распределения видности интерференционных полос
Выясним теперь, к каким изменениям в наблюдаемых интерферограммах приведет изменение размеров м формы входного зрачка наблюдательной системы,
При получения выражения (14) мы использовали предположение о малости размеров круглого отверстия входного зрачка с тем. чтобы Фурье-образ функции его пропускания, т.е. ширина импульсного отклика наблюдательной системы, значительно превышал наибольшую величину относительного смещения точек изображения объекта. В этом случае два срекл-поля оказываются пространственно-когерентными (в смысле образования низкочастотной интерферограммы) в силу суперпозиции идентичных элементарных областей когерентности, и наблюдаемая нитерферограмма имеет высоким контраст по всему полю изображения.
При увеличении размеров зрачка увеличивается разрешение системы, т.е. уменьшается ширина импульсного отклика. Следовательно,
- 80 -
но, в силу вращательного характера смещения, сокращается зона, где имеет место суперпозиция идентичных областей когерентности, и два спекл-поля оказываются пространственно когерентными не по всему полю изображения. Наибольшее перекрытие идентичных элементарных областей когерентности (спеклов) имеет место там, где происходит наименьшее относительное смещение световых полей, я именно там должен наблюдаться максимальный контраст интерференционных полос, указывающий на положение области локализации интерферограммы /16/.
В рассматриваемом случае объектное световое поле не испытывает смещения на оси своего поворота, определяемой уравнением (7). Следовательно, голографическая интерферограмма вращательного сдвига локализована вблизи прямой линии, ориентация которой зависит от направления освещения объекта и ориентации оси его вращения . Этот вывод полностью согласуется с результатами, полученными в /17/ на основе геометрической теории локализации.
На рис.2 приведены снимки интерферограмм, иллюстрирующие сокращение области когерентности с увеличением входного зрачка наблюдательной системы.
При значительных размерах отверстия входного зрачка в выражениях для комплексных амплитуд необходимо учесть относительный вращательный сдвиг между изображениями. Представим соответствующие выражения в виде
- 81 -



а) б) в)
Рис.2. Голографические интерферограммы, полученные в случае круглого зрачка при относительных отверстиях 1:8 (а), 1:4 (б), 1:2 (в).
- 82 -
где
|
a0 = w
z(y30 – y3) |
(18) |
|
b0 = w
z(-x30 + x3) |
Для интерпретации соотношений (16) и (17) диффузно отражающую поверхность объекта полезно представить в виде набора когерентных точечных источников света со случайной начальной фазой /18,19/. Тогда в плоскости изображения комплексная амплитуда светового поля может быть представлена набором функций p(х3,у3), в пределах области существования которых фаза является детерминированной величиной и меняется случайный образом при переходе от одной такой области к другой. При этом предполагается, что наблюдательная система не разрешает точечные источники на поверхности объекта. Комплексный коэффициент отражения поверхности в этом /19/ случае удобно представить в виде
t(x,y) = t0(x,y)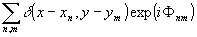 (19)
(19)
где Фnm - случайная начальная фаза световой веяны в точке xnym. Из (16) и (17) следует, что интенсивность в плоскости изображения с точностью до постоянного коэффициента описывается соотношением:
|
i(x3,y3) = |
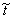 (x3,y3)Ä
p(x3,y3)|
2 + | (x3,y3)Ä
p(x3,y3)|
2 + |
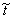 (x3 – a0,y3 – b0)Ä
p(x3,y3)|
2 + (x3 – a0,y3 – b0)Ä
p(x3,y3)|
2 + |
(20) |
|
+ 2re{exp[iy
(x3,y3)]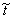 (x3,y3)Ä
p(x3,y3) (x3,y3)Ä
p(x3,y3)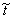 *(x3- a0,y2 – b0)Ä
p*(x3,y3)} *(x3- a0,y2 – b0)Ä
p*(x3,y3)} |
- 83 -
Здесь первые два слагаемых с учетом (19) описывают спекл-структуру в исходном и смещенном состояниях объекта, тогда как третье слагаемое - интерференционный член - описывает интерферограмму. Для исключения из рассмотрения спекл-модуляции проведем усреднение по пространственным координатам, Тогда (20) примет вид:
|
<|
i(x3,y3)|
> = <|
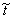 (x3,y3)Ä
p(x3,y3)|
2> + <| (x3,y3)Ä
p(x3,y3)|
2> + <|
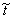 (x3 – a0,y3 – b0)Ä
p(x3,y3)|
2> + (x3 – a0,y3 – b0)Ä
p(x3,y3)|
2> + |
(21) |
|
+ 2re{exp[iy
(x3,y3)]<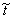 (x3,y3)Ä
p(x3,y3) (x3,y3)Ä
p(x3,y3)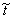 *(x3- a0,y2 – b0)Ä
p*(x3,y3)>} *(x3- a0,y2 – b0)Ä
p*(x3,y3)>} |
Здесь первые два слагаемых описывают среднюю интенсивность исходного и смещенного изображений объекта. Полагая эти интенсивности равными, получим для видности интерференционных полос выражение
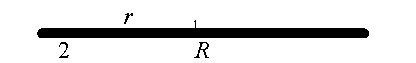 (22)
(22)
Пусть t0 = (x,н) = 1 для всей поверхности объекта. Тогда, подставляя (11) и (19) в (22) и опуская несущественные детерминированные фазовые множители, получим:
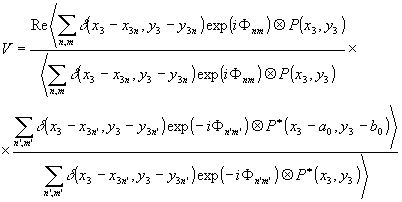 (23)
(23)
где было использовано свойство коммутативности свертки. Далее,
- 84 -
используя фильтрующее свойство дельта-функции, приведем (23) к виду:
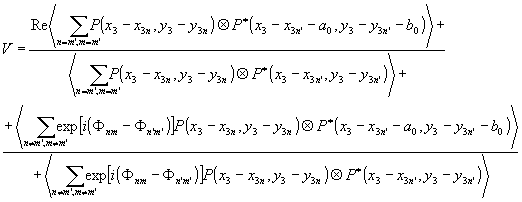 (24)
(24)
Поскольку, в силу случайности значений Фnm на площади усреднения, Фnm-Фn’m’ также является оду чайной величиной, равномерно распределенной в интервале 2p
, то вторые слагаемые в числителе и знаменателе (24) в результате усреднения оказываются равными нулю. Производя суммирование в первых слагаемых, получаем
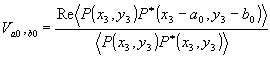 (25)
(25)
В (25) усреднение выполнено по площади, значительно превышающей область, где функция p(x3,y3) заметно отличается от нуля. Следовательно, пределы интегрирования можно распространить до бесконечности и зализать (25) в виде
- 85 -
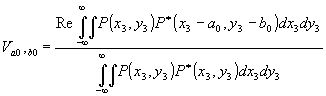 (26)
(26)
Преобразуем (25), используя теорему свертки:
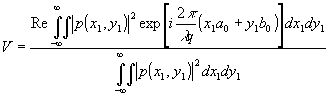 (27)
(27)
Выражения, стоящие в числителях (26) и (27), являются автокорреляционной функцией поля в плоскости изображения /14/. Сами же выражения (26) и (27) определяют нормированную функцию автокорреляции спекл-поля, т.е. являются нормированными комплексными коэффициентами когерентности. Таким образом, имеет место полное совпадение с формулировкой теоремы Ван Циттерта-Цернике /14,20/, если в качестве источника света рассматривать зрачок наблюдательной системы, освещаемый диффузно-когерентным светом.
Если функция пропускания зрачка равна единице в пределах его отверстия и нулю за его пределами, то |
p(x1,y1)|
2 = p(x1,y1) (27) примет вид:
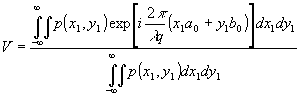 (28)
(28)
- 86 -
Здесь опущен знак rе, поскольку Фурье-образ бинарного зрачка является величиной действительной.
Таким образом, видность голографической интерферограммы определяется как нормированный Фурье-образ функция пропускания зрачка наблюдательной системы. При этом, пространственными частотами Фурье-преобразования являются величины x
0 = a0/l
q и h
0 = b0/l
q, определяющие относительное смещение изображений. Поэтому видность зависит как от вида функции Р(x
0,h
0) = f[p(x,y)], так и от величин a0 и b0. Поскольку а0 и b0 являются линейными функциями координат, то функция v(a0,b0) по своему виду будет отличаться от нормированного Фурье-образа функции пропускания зрачка только масштабом.
4. Роль формы входного зрачка изображают системы
Из выражения (28) следует, что v =1 при условий a0 = b0 =0, т.е. в неподвижной точке Р’0 изображения, что соответствует сделанному выше выводу о локализации интерферограммы вращательного сдвига. В этой связи при дальнейшем анализе удобно будет считать, что центр вращения изображения совпадает с началом системы координат x3, у3. Тогда (28) и учетом (18) принимает вид:
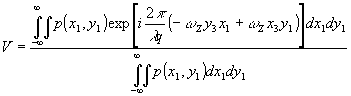 (29)
(29)
- 87 -
Рассмотрим теперь зрачки различной формы и получим соотношения для видности соответствующих интерферограмм.
4. Круглый зрачок
Для такого зрачка достаточно рассмотреть изменение видности вдоль какого-либо радиус-вектора 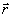 3. Выражение (29) для этого случая принимает вид:
3. Выражение (29) для этого случая принимает вид:
vw
z(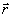 3) = 2j1(t
)/t
(30)
3) = 2j1(t
)/t
(30)
где j1(t
) - функция Бесселя первого рода первого порядка, а
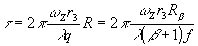 (31)
(31)
График функции вида (30) хорошо известен. Поскольку первый нуль функции 2j1(t
)/t
соответствует значению t
= 3.83, то видность падает до нуля в точках с радиус-вектором 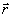 31, модуль которого определяется из соотношения
31, модуль которого определяется из соотношения
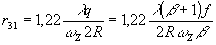 (32)
(32)
Принимая во внимание характерный размер спеклов, который для круглого зрачка принято определять /21/ соотношением
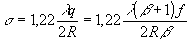 (33)
(33)
- 88 -
убеждаемся в том, что видность интерферограммы падает до нуля в тех областях изображения, где относительное смещение достигает характерного размера спеклов 2) в этой плоскости. Ниже мы увидим, что за этим падением видности до нуля следуют "всплески" и падения видности, определяемые вторичными максимумами и нулями функции (30).
Вернемся к рис.2,на котором приведены снимки интерферограмм, полученные при различных значениях относительного отверстия ¦
/2r объектива фотоаппарата. Видно, что при увеличении относительного отверстия уменьшается область, где контраст полос близок к единице. Кроме того, достаточно отчетливо наблюдается осцилляция видности по мере удаления от центра вращения, хотя во вторичных максимумах видность существенно меньше, чем в главном. Тем не менее, можно заметить, что при переходе от одного максимума видности к другому интерференционные полосы испытывают поперечный сдвиг на половину периода, что соответствует изменению фазы на p
. Можно в этой связи считать, что видность в определенных областях принимает отрицательное значение, и её можно представить в комплексной форме:
vw
z(r3)= |vw
z(r3)|exp(ij
) (34)
где j
- фаза видности, характеризующая сдвиг интерференционных полос при переходе видности через нулевое значение.
2) При определении размеров спеклов с помощью (33) предполагается, что они представляют собой пятна с практически однородной освещенностью.
- 89 -
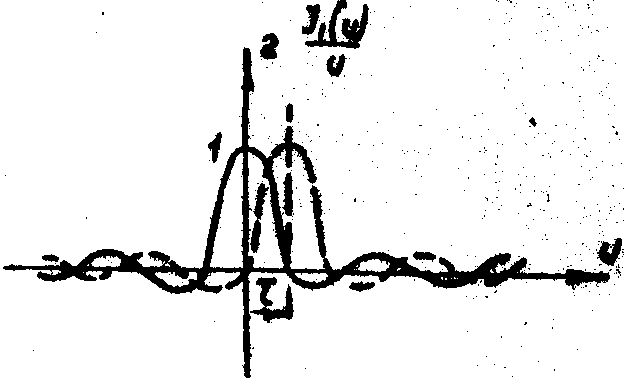
Поясним эффекты осцилляции видности и "сбоя" её фазы, рассматривая различные степени перекрытия элементарных областей когерентности, световое поле в которых представляет собой Фурье-образ функции пропускания зрачка. На рис.3 схематически представлено нормированное распределение амплитуды в такой области когерентности для четырех характерных участков плоскости изображения в случае круглого зрачка. В точке Р'0 (рис.3а) элементарные области когерентности (спекли) исходного и смещенного световых полей полностью совпадают, и эта точка соответствует максимуму интерференции (центру светлой интерференционной волосы). С удалением от этой точки, т.е. с ростом t
уменьшается степень перекрытия элементарных областей когерентности, и интенсивность светлой полосы уменьшается. Рис.3б соответствует ситуации, когда главный максимум одного спекла совпадает с первым нулем другого (t
= 3.83) - при этом контраст падает до нуля. Далее, (рис.3в) , главный максимум одного спекла совпадает с первым максимумом другого, имеющим отрицательное значение, и амплитуды оказываются в противофазе, т.е. светлая интерференционная полоса переходит в темную (сдвиг на p
). В силу различия значений амплитуд в главном и первом максимумах функция 2j1(t
)/t
видность в этом участке значительно ниже, чем в окрестностях точки Р’0 (»
0,13). При дальнейшем удалении от центра вращения видность снова падает до нуля, а затем наступает совпадение глазного максимума уже со вторым, имеющим положительное значение (рис.3г), и вновь происходит сдвиг полос на половину периода, а видность оказывается еще меньше. Аналогичный анализ .нетрудно провести и для темной полосы интерференционной картины.
- 90 -
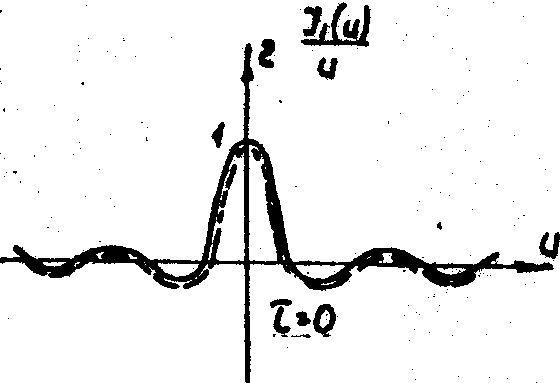
а) б)
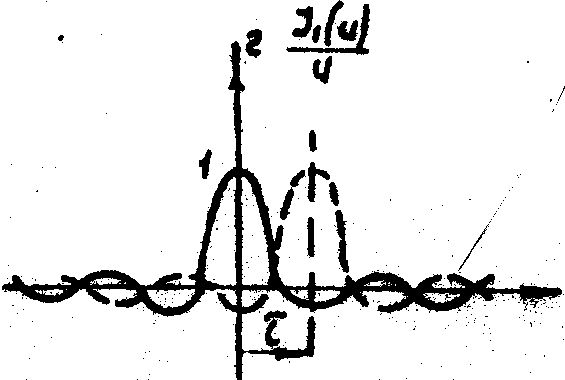
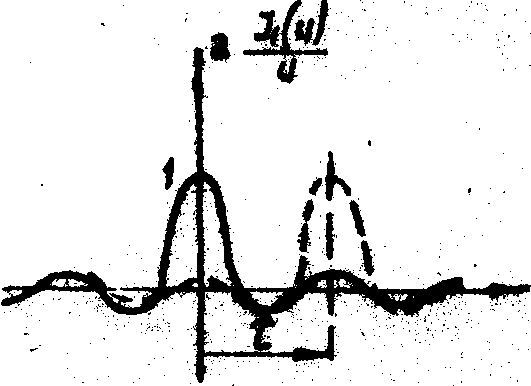
в) г)
Рис.3. Когерентное сложение двух идентичных спеклов для круглого зрачка при различней степени их относительного смещения. а - полная корреляция, б - декорреляция, в,г >- частичная корреляция.
- 91 -
В наших экспериментах было замечено, что направление сдвига интерференционных полос зависит от направления вращательного смещения объекта, что объясняется соотношением между направлениями изменения фазы интерференционной картины и фазы в пределах элементарной области когерентности.
Отметим, что на наличие осцилляции видности голографических интерферограмм обращал внимание ряд авторов (см., например, /3/), однако, их природа оставалась невыясненной. Замечание о связи этого эффекта со взаимным смещением спеклов имеется в теоретических работах /22,23/, в которых, кроме того, машинный расчет показал наличие сбоя интерференционных полос. Однако, ограничение видности в расчетах значением, не меньшим О,1, не позволило выявить более одного вторичного "всплеска" видности, поскольку рассматривался только зрачок круглой формы.
Между тем, формирование интерференционной картины с использованием зрачков другой - более сложной - формы позволяет более полно и убедительно выявить аффекты осцилляции видности интерференционных полос и их сбоя на полпериода после каждого прохождения области с нулевой видностью, а также связать эти эффекты с тонкой структурой амплитудно-фазового распределения в пределах индивидуального спекла.
б. Кольцеобразный зрачок
Пусть внешний диаметр кольцеобразного зрачка равен Р, а внутренний -m
r (0<m
<1). Тогда импульсный отклик изображающей системы определяется (см., например, /24/) соотношением
- 92 -
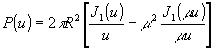 (35)
(35)
где u = 2p
rr3/l
q.
Видность интерференционных полос, рассчитанная по формуле (29), имеет вид:
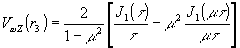 (36)
(36)
где t
определяется выражением (31).
Если m
»
1, т.е. имеется узкое кольцо, то (35) принимает вид:
vw
z(r3) = j0(t
) (37)
где j0(t
) - функция Бесселя первого рода нулевого порядка.
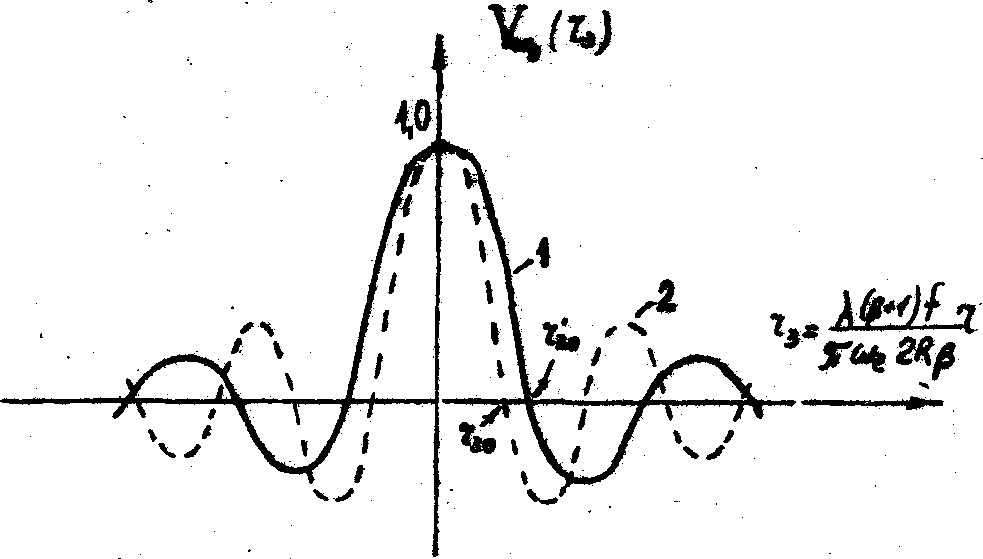
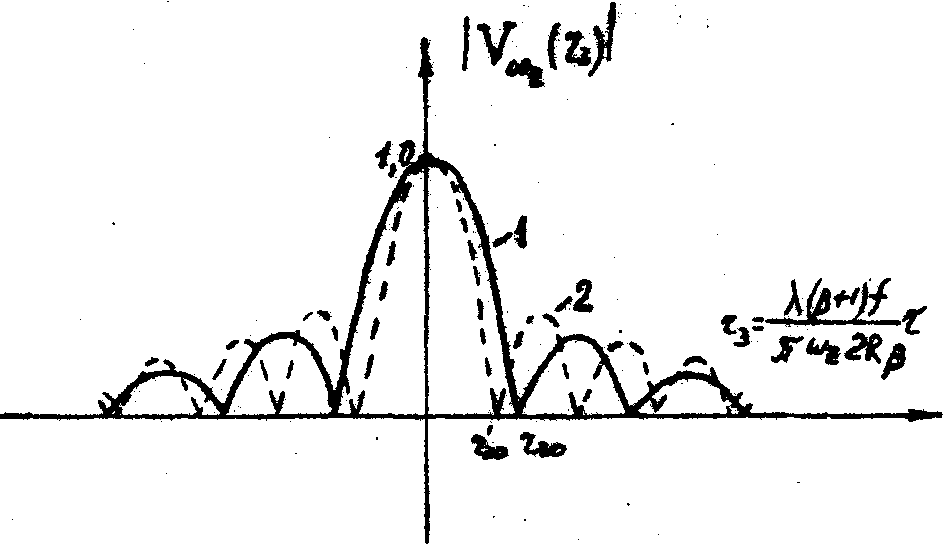
Графики функций (36) и (37), соответственно, для m
= 0,66 (машинный расчет) и m
»
1 приведены на рис.4 а,б. Очевидно, что в случае кольцеобразного зрачка уменьшение видности происходит заметно медленнее, чем в случае круглого зрачка, а пространственная частота осцилляции видности - выше. При этом, чем уже кольцо, тем больше амплитуда вторичных максимумов и тем выше частота осцилляции.
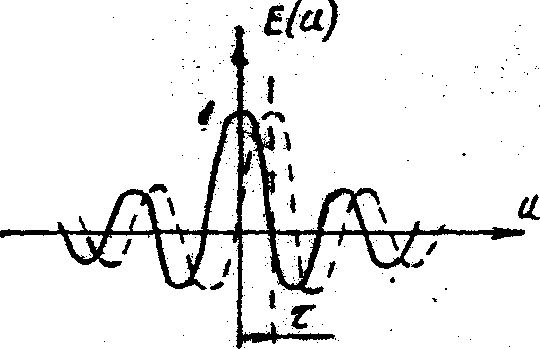
Плавное уменьшение видности от главного ко вторичным её максимумам, а также эффекты осцилляции видности и сдвига полос на p
нетрудно объяснять, пользуясь рис.5, на котором схематически показано распределение амплитуд в перекрывающихся идентичных спеклах для четырех характерных значений их относительного смещения подобно тому, как это было сделано выше для круглого зрачка.
- 93 -
а)
б)
Рис.4. Закономерность измерения видности (а) и модуля видности (б) интерферограммы вращательного сдвига для кольцеобразного зрачка при m
= 0,66 (1) и m
= 1,0 (2).
- 94 -
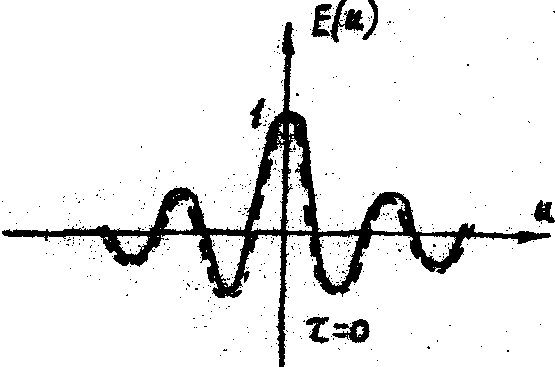
а) б)
в) г)
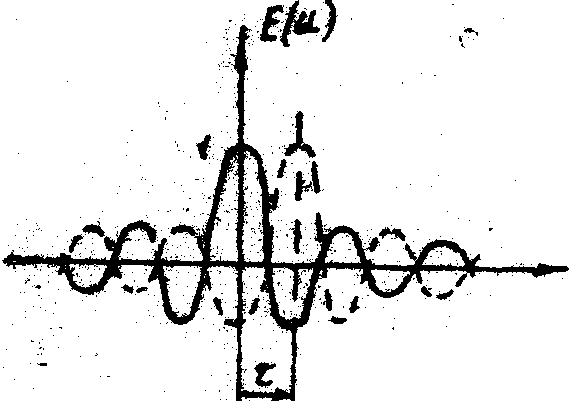
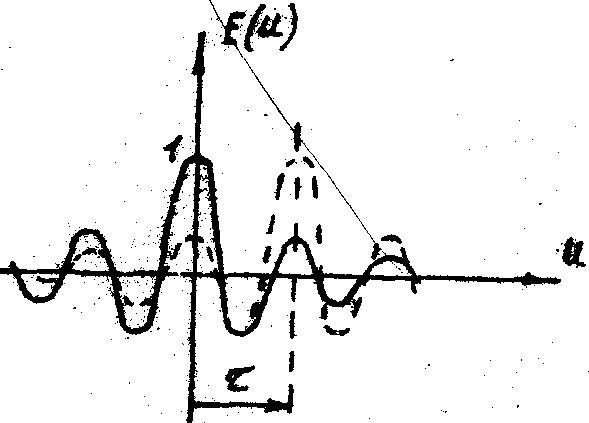
Рис.5. Когерентное сложение двух идентичных спеклов для кольцеобразного зрачка при различной степени их относительного смещения.
- 95 -
На рис.6а приведен снимок интерферограммы, сформированной с использованием кольцеобразного зрачка при следующих условиях эксперимента: r=14,5 мм, m
= 0,66, b
= 0,1, ¦
/2r = 2, l
= 0,63 мкм. w
z »
4’.
График зависимости интенсивности зарегистрированных интерференционных полос от смещения, полученный путём фотометрирования негатива этого снимка, приведен на рис.6б, а соответствующие значения видности, нанесенные на теоретический график, - на рис.4а. Отчетливо видны осцилляции контраста и сбои периода полос при переходе от одного максимума к другому. Отличие значений видности в главном максимуме от теоретических значений обусловлено, нелинейностью фотографического процесса.
в. 3рачок в виде двух параллельных щелей
Пусть две одинаковые параллельные щели с длиной ℓ1 и шириной ℓ2, расстояние между центрами которых равно l, ориентированы длинными сторонами вдоль оси х1. Тогда, для видности интерференционных полос по ортогональным осям получим соотношения:
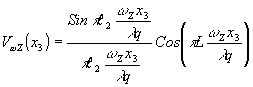 (38)
(38)
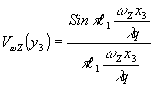 (39)
(39)
- 96 -

а)
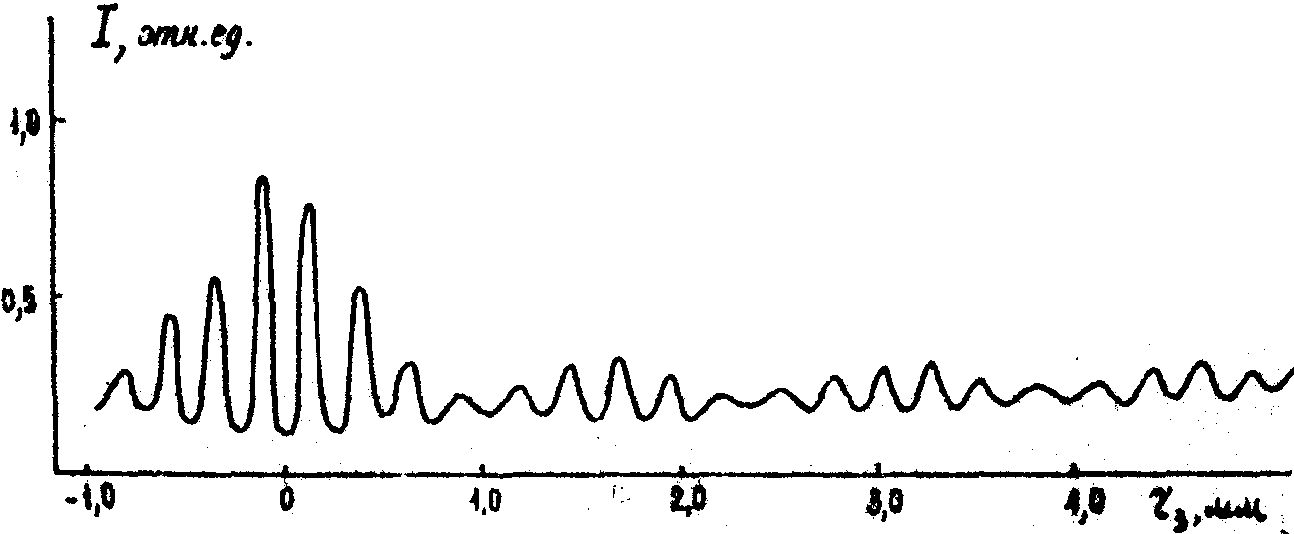
б)
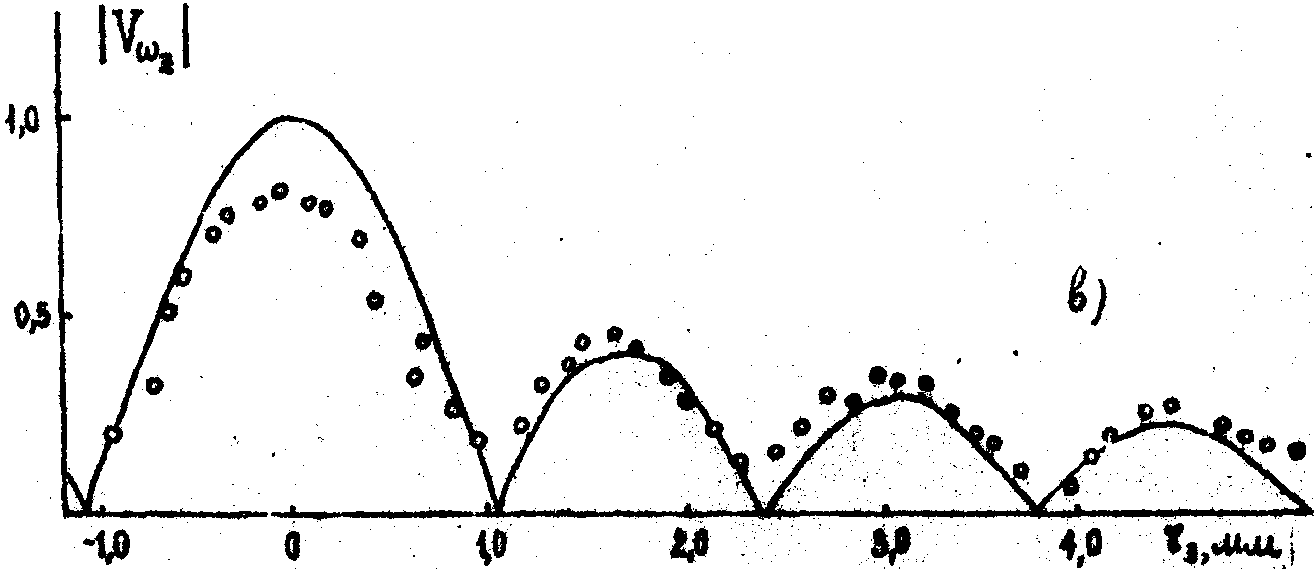
в)
Рис.6. Голографическая интерферограмма вращательного сдвига, полученная с кольцеобразным зрачком (a), соответствующая микрофотограмме (б), и график распределения видности (в).
- 97 -
В этом случае видность интерферограммы промодулирована в направлении длинной стороны щелей функцией cos(p
lw
zx3/l
q), поскольку импульсный отклик система промодулирован в направлении у3 функцией cos(p
lw
zx3/l
q), а асимметрия области, занимаемой интерферограммой. обусловлена различием размеров спеклов по осям х3 и у3.
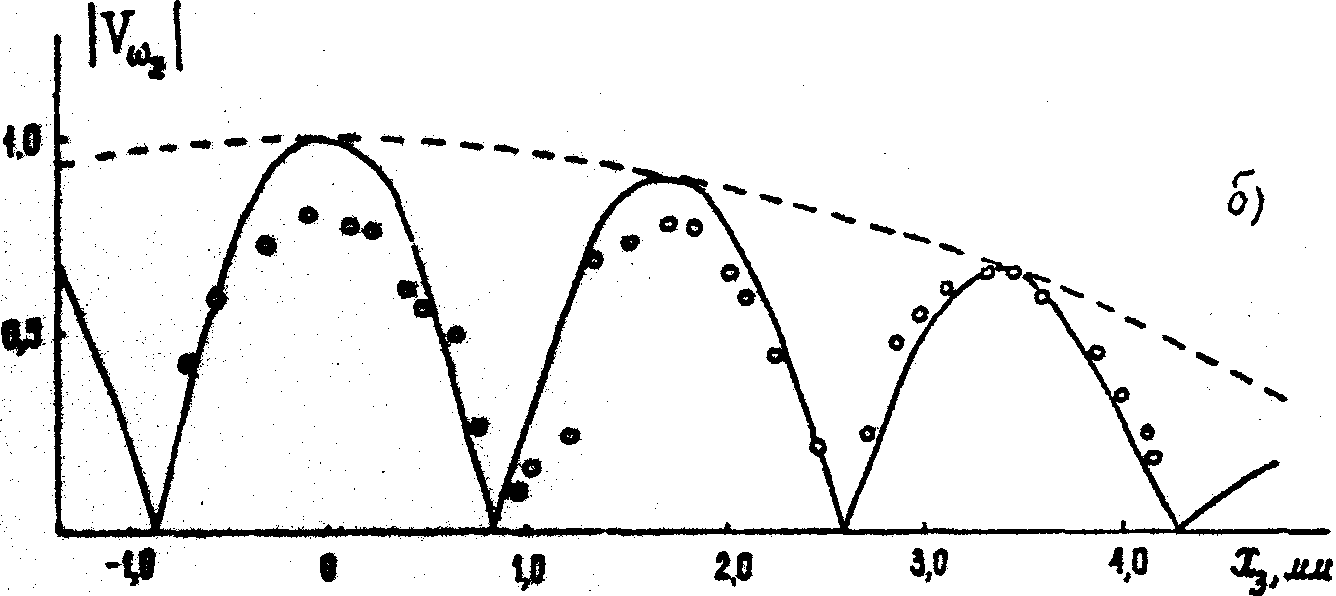
График видности интерференционных полос для двухщелевого зрачка приведен на рис.7. Нетрудно убедиться, что видность осциллирует с пространственной частотой, пропорциональной расстоянию между щелями, а скорость уменьшения видности определяется шириной щелей. Поэтому для узких и далеко разнесенных щелей амплитуда осцилляции видности медленно убывает при высокой пространственной частоте этих осцилляции, что иллюстрируется рис.8, на котором приведены снимки интерферограмм для разных двухщелевых зрачков.
Нетрудно оценить характер распределения видности для зрачков другой формы. Так, например, для применяемого в спекл-интерферометрии /25/ зрачка из двух круглых отверстий центрально симметричная модуляция видности Бесселевой функцией первого рода первого порядка будет сочетаться с модуляцией косинусоидальной функцией вдоль одного направления.
Подчеркнем, что все описанные эффекты проявляются также и при обеспечении наложения взаимно-сдвинутых спекл-полей средствами спекл-интерферомегрии, причем очевидно, что рассмотренные особенности поведения спекл-полей проявляются и при других видах смещений.
Отметим, что измерение видности интерференционных полос или размеров областей, на границах которых видность падает до нуля,
- 98 -
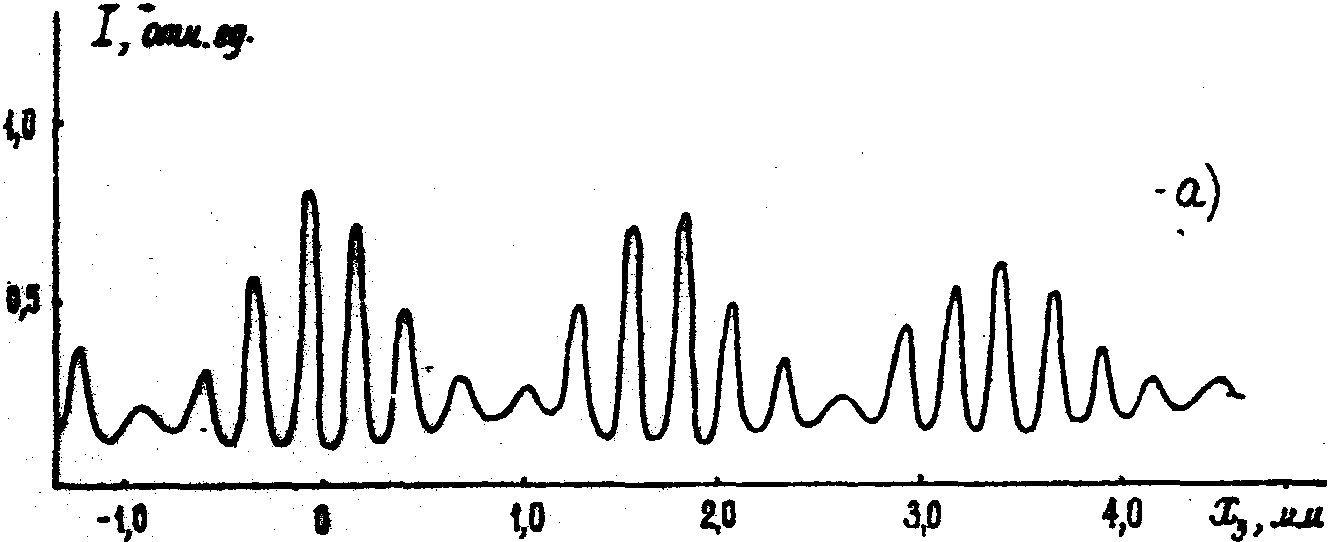
а)
б)
Рис.7. График видности интерференционных полос для двухщелевого зрачка (теория и эксперимент).
- 99 -

а)

б)
Рис.8.
- 100 -
позволяет определить величину смещения - в нашем случае угол поворота объекта. Например, для кольцеобразного зрачка с отношением радиусов m
= 0,66 первый нуль функции видности соответствует значению t
= 2,62. Подставляя это значение в выражение (31) и измеряя в плоскости изображения или по негативу фотоснимка значение r3, получаем для реальных параметров l
, r, ¦
/2r и b
значение w
z.
5. Заключение
Закономерности образования интерференционных картин, формируемых при наложении двух идентичных, но сдвинутых друг относительно друга спекл-полей, свидетельствуют о том, что размеры и геометрическая структура областей существования интерференционных полос, а также распределение видности последних определяются главным образом тонкой структурой элементарных областей когерентности (спеклов), однозначно связанной с импульсным откликом изображающей системы.
В этой связи с понятием индивидуальных спеклов следует связывать представление не о пятнах с постоянной амплитудой и фазой, а об областях с достаточно сложным распределением комплексной амплитуды, все участки которых вносят вклад в формирование наблюдаемых интерференционных полос.
Выбор размеров и особенно формы входного зрачка позволяет в широких пределах управлять этим распределением комплексной амплитуды и наглядно выявить такие эффекты, связанные с тонкой структурой индивидуальных спеклов, как осцилляции видности интерференционных полос, их сдвиг на половину периода при переходе
- 101 -
через нуль видности, визуализация функции пространственной когерентности спекл-поля.
Индивидуальные спеклы можно рассматривать как своеобразные "поперечные моды” спекл-поля, поскольку только при перекрытии идентичных спеклов (или их участков) образуется низкочастотная интерференционная картина с отличной от нуля видностью.
Визуализация посредством регистрации распределения видности функции поперечной когерентности спекл-поля является наглядным образом, отражающим к тому же распределение комплексной амплитуды в индивидуальном спекле при выборе той или иной формы зрачка изображающей системы или самого диффузно рассеивающего объекта.
Выявленные особенности спекл-полей позволяют прояснить и углубить объяснение поведения голографических интерферограмм, получаемых в диффузно рассеянном излучении, в первую очередь, закономерности локализации и уменьшения видности, связав их непосредственно с параметрами индивидуальных спеклов,
Необходимо отметить определенные аналогии с особенностями, проявляющимися при взаимном наложении спекл-поля и однородного поля /10/ - в дислокациях также имеется сбой на половину периода, причем имеются сбои с противоположными знаками.
В целом, результату настоящей работы могут представить интерес во всех случаях, когда необходим детальный анализ структуры спекл-поля или имеет место суперпозиция световых полей, содержащих спекл-структуры.
Авторы благодарят Г.В.Скроцкого за обсуждение результатов.
- 103 -
Литература
1. dainty j.o., welford w.t. opt.comm., 1971, 3, 289.
2. Клименко И.С., Матинян Е.Г., Скроцкий Г.В. ДАН СССР, 1973, 211, 571.
3. Вест Ч„ Голографическая интерферометрия, М., Мир. 1982,
4. Зельдович Б.Я., Поповичев В.И., Рагульский В.В., Файзуллов Ф.С;. Письма в ЖЭТФ, 1972, 15, 160.
5. Куликов О.Л., Пилипецкий Н.Ф., Сударкин А.Н., Шкунов В.В. Письма в ЖЭТФ. 1980, 31, 377.
6. labeyrie a. astron. astrophys., 1970, 6, 85.
7. archbold e, ennos a.e. opt.acta, 1972, 19, 253.
8. Франсон М. Оптика спеклов. М., mир, 1980.
9. Клименко И.О., Рябухо В.П. Материалы Хiv Всесоюзной школы по голографии. Л., 1083, с.191.
10. Баранова Н.Б.. Зельдович Б.Я.. Мамаев А.В., Пилипецкий Н.Ф., Шкунов В.В. ЖЭТФ, 1962, 83, 1702.
11. Кольер Р., Беркхарт К., Лин Л. Оптическая голография, М., Мир, 1973.
12. Гудмен Дж. Введение в Фурье-оптику, М., Мир, 1970.
13. Власов Н.Г., Штанько А.Е. Материалы viii Всесоюзной икота по голографии, Л., 1975, с.191.
14. goodman j.w. laser speckle and related phenomena (ed j.dainty), springer-verlag, berlin, 1975, p.9.
15. Александров Е.Б., Бонч-Бруевич М.А., ЖТФ, 1967, 37, 517.
16. stetson k.a. j.opt.soc.am., 1976, 66, 1267.
17. molin n.e., stetson k.a. optik, 1970, 31, 281.
- 103 -
18. goldfischer. j.opt.soc.am., 1965, 55, 247.
19. dainty j.С. progress in optics (ed Е.wolf), 1976, 14, 3.
20. Власов Н.Г., Скроцкий Г.В., Соловьев Е.Г. В сб. "Проблемы голографии", 1973, вып.1, 85.
21. ennos А.Е. laser speckle and related phenomena (ed j.dainty), springer-verlag, berlin, 1975, p.203,
22. i.yamaguchi. opt.acta, 1977, 24, 1011.
23. i.yamaguchi. opt.acta, 1978, 25, 299.
24. Папулис А. Теория систем и преобразований в оптике, М., Мир, 1971.

