|
|
 |
 |

|
| |
КОРРЕЛЯЦИОННЫЕ СВОЙСТВА ПРОШЕДШИХ РАССЕИВАЮЩУЮ СРЕДУ ПУЧКОВ И КАЧЕСТВО ОТОБРАЖЕНИЯ ИНФОРМАЦИИ МЕТОДАМИ ГОЛОГРАФИИ
В.Г.Синченко
Анализируется выполнимость условия пространственной инвариантности степени когерентности излучения m
(u,u') в точках с координатами u и u' двух пятен размытая линии системы рассеивавшая среда - объектив. Установлено, что величина m
(u,u') является пространственно-инвариантной функцией в пределах узких зон пятен размытия. Показана возможность определения m
(u,u') из анализа картин дифракции на щелях прошедшего среду и объектив пучка.
При создании систем видения, в которых используются голографические методы компенсации амплитудно-фазовых искажений, вносимых рассеивающей средой в объектный пучок /1/, могут использоваться схемы голограммы Фурье /2/, Френеля /3/, а также голограммы сфокусированного изображения /4/. Последняя перспектива с источниками частично-когерентного излучения /5/. Во всех случаях важна информация о корреляционных свойствах прошедших среду пучков, определение взаимосвязи свойств излучения с оптическими характеристиками сред. В частности, при оценке качества изображения систем, использующих схему голограммы сфокусированного изображения, необходимы данные о степени когерентности (СК) двух пятен размытия линий m
(u,u') (u, u' - отклонения рассматриваемых точек от точек идеального изображения линий). Данные о m
(u,u') требуются при решении прямой и обратной задачи оптического изображения, а изучение взаимосвязи m
(u,u') и оптических характеристик среды позволяет решать важные для практики задачи: оценивать возможность и эффективность получения информации через рассеивающую среду голографическими методами, а также прогнозировать по известным характеристикам сред качество формируемого системой изображения.
- 49 -
Использование для получения изображений через рассеивающую среду варианта голографии сфокусированного изображения оправдывается также большей интенсивностью объектного пучка в плоскости регистрации и меньшими требованиями к виброзащите системы и когерентности источника излучения по сравнению, например, с голограммой Френеля /6/. Кроме того, на стадия восстановления голограммы в этом случае возможно использовать протяженные полихроматические источники излучения /7/.
В данной работе анализируется выполнимость условия пространственной инвариантности величины m
(u,u') в системе среда-объектив. Анализ выполнен по результатам экспериментальных исследований СК излучения между точками одного пятна размытия линии и опорной точкой /8/. Рассмотрена возможность нахождения значений m
(u,u') из анализа картин дифракции прошедшего среду и объектив пучка на щелях, помещаемых в плоскость изображения системой двух линий.
Для когерентного освещения величину m
(u,u') можно найти, если известна СК излучения между точками одного пятна размытия линии и опорной точкой m
(u,а). Здесь u - отклонение рассматриваемой точки в пятне размытия от точки идеального изображения линии, а - координата опорной точки. Действительно, представим функции взаимной интенсивности j(u,a) и j(u',a) в изображении двух освещенных точечным монохроматическим источником линий через возмущения v(s,u), v(s,u'), v(s,a) в точках u, u', a по формуле Гопкинса /9/:
j(u,a) = v(s,u)v*(s,a) = 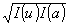 m
(u,a), j(u',a) = v(s,u')v*(s,a) = m
(u,a), j(u',a) = v(s,u')v*(s,a) = 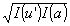 m
(u',a) m
(u',a)
Здесь i(u), i(u'), i(a) - интенсивности точек с координатами u, u' и a, соответственно. Образуя произведение j(u,a)j*(u',a) и учитывая, что j(u,u')=v(s,u)v*(s,u')= =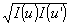 m
(u,u'), получаем для |m
(u,u')|
и j
(u,u')=argm
(u,u')-argm
(0,0) соотношения: m
(u,u'), получаем для |m
(u,u')|
и j
(u,u')=argm
(u,u')-argm
(0,0) соотношения:
|
m
(u,u')|
= |
m
(u,a)|
|
m
(u',a)|
, j
(u,u') = j
(u) - j
(u') (1)
- 50 -
Эти соотношения справедливы только в случае полностью когерентного освещения в ненарушающей когерентность оптической системе. Отметим, что по физическому смыслу j
(u,u') с точностью до постоянной совпадает с фазой m
(u,u').
Значения m
(u,a) можно найти экспериментально, анализируя вbдность и положение интерференционных полос, образованных за двумя анализирующими щелями /10/. Они связаны с модулем h(u) и фазой j
(u) амплитудной функции размытия линии, определяющей качество изображения системой когерентно освещенных объектов, соотношениями
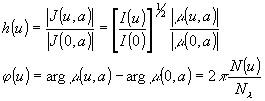 (2) (2)
где n(u) - смещение полос, nl
- смещение полос, соответствующее изменении разности хода на длину волны. Из соотношения (2) видно, что j
(u) совпадает с фазой m
(u,a) с точностью до постоянной.
В работе /8/ на модельных средах (растворы молока в воде) для случая когерентного освещения найдены зависимости |m
(u,a)|
и j
(u) при вариациях такой характеристики рассеивающей среды как оптическая толщина /11/. В качестве формирующего изображения использовался двухлинзовый объектив с фокусным расстоянием 135 мм. В результате исследований показано, что с увеличением оптической толщены от 0 до 20 величина |
m
(u,a)|
уменьшается для всех u. Максимум |
m
(u,a)| соответствует точкам идеального изображения. Уменьшение значений |
m
(u,a)|
есть следствие нарушения когерентности в системе среда-объектив за счет подвижности рассеивающих частиц. Значения j
(u) в указанном диапазоне оптических толщин не зависят от толщины среды, что связано с малостью угль приема излучения в формирующей изображение системе и усреднением рассеянной части излучения объектного пучка, когда изображение формируется только прямопрошедшим излучением.
- 51 -
Вследствие вышесказанного из данных о m
(u,a), m
(u',a) по /1/ можно рассчитать только величину j
(u,u'). Рассчитать |
m
(u,u.')|
не представляется возможным.
На рис.1а представлена зависимость j
(u,u') от u, u', найденная из данных работы /8/. Как видно, эта зависимость, характеризующая систему в диапазоне оптических толщин от 0 до 20, представляется достаточно сложной. При симметричной j
(u) j
(u,u') также симметрична относительно осей О-u, 0-u'. Для точек u = u' = 0 j
(u,u') принимается равной нулю. Кроме того, j
(u,u') º
0 для всех u при u = u'. В зависимости от u и u' могут реализовываться ситуации, когда j
(u,u') принимает положительные или отрицательные значения. Это соответствует опережению или задержке соответственно прихода волн в точку наблюдения в одном пятне размытия по отношению к точке наблюдения в другом пятне.
Рассмотрим, удовлетворяют ли условию пространственной инвариантности значения m
(u,u') в случае формирования изображения когерентно освещенного объекта нарушающей когерентность системой среда-объектив. Это условие, как известно, заключается в выполнении равенства m
(u,u') = m
(u-u'), которое, в силу комплексности m
(u,u'), эквивалентно равенствам:
|
m
(u,u')|
= |
m
(u - u')|
, j
(u,u') = j
(u - u') (3)
В этом случае m
(u,u') является функцией разности координат рассматриваемых точек и не зависит от координат точек.
Рассмотрим выполнение (3), исходя из рис.1а. Из него следует, что j
(u,u') зависит не от u - u', а от координат u, u'. Так, например, при u - u' = 20 мкм для u = 30 и u = 150 мкм j
(u,u') = -2,4p
и -3,8p
, соответственно. Кроме того, для системы среда-объектив можно предположить, что величина |
m
(u,u')|
не является пространственно-инвариантной функцией. Предпосылкой итого предположения является уменьшение значений |m
(u,u')|
для всех u при росте оптической толщины среди. Отметим, что в ненарушающей когерентность системе, например, объективе, при когерентном освещении объекта |
m
(u,u')|
= |
m
(u - u')|
= 1 для всех u, u'.
- 52 -
Однако, даже в такой системе m
(u,u') не является пространственно-инвариантной функцией из-за нарушения второго из соотношений (3). В то же время СК m
(u,u') приближенно можно считать пространственно-инвариантной функцией, если рассматривать m
(u,u') не между всеми точками двух пятен размытия, а только в пределах ограниченных по u и u' интервалов. Остановимся на этом подробнее.
Представим пятно размытия линии системы состоящим из ряда зон, примыкающих друг к другу. Рассмотрим в пределах зоны зависимость j
(u). Если ширина зоны достаточно мала, то в пределах зоны j
(u) можно аппроксимировать линейной функцией, a j
(u) во всем диапазоне изменений u заменить на кусочно-линейную функцию j
a(u). Аналогично рассмотрим второе пятно размытия линии в заменим j
(u') на j
a(u'). Рассчитаем по аналогии с (3) аппроксимирующую функцию
j
a(u,u') = j
a(u) - j
a(u') (4)
Если число зон таково, что j
a(u) »
j
(u), j
a(u') »
j
(u'), то j
a(u,u') »
j
(u,u'). В то же время в пределах каждой пары зон j
a(u,u') = j
(u – u'). Действительно, так как j
а(u) и j
a(u') в пределах зон линейно зависят от u и u', то значения j
а(u,u') рассчитанные по (4), также будут линейной функцией. Геометрическая интерпретация этого утверждения означает, что в пределах двух зон значения j
a(u,u') в координатах u, u', j
будут находиться в одной плоскости. Тогда, в пределах любой пары зон j
а(u,u') зависит только от разности u – u' и не зависит от координат u, u'. В отношении пространственной инвариантности |
m
(u,u')|
в пределах зон отметим следующее. Если ширина зон мала, то при произвольной, не имеющей точек разрыва функции |
m
(u,u')|
в пределах каждой пары зон с небольшой погрешностью, |
m
(u,u')|
можно считать постоянной. В этом случае |
m
(u,u')|
= |
m
(u - u')|
= const является пространственно-инвариантной функцией. Таким образом, СК излучения между точками двух пятен размытия линий системы среда-объектив не является пространственно-инвариантной функцией при рассмотрении всех точек пятен размытия.
- 53 -
Однако её можно считать пространственно-инвариантной в пределах узких зон пятен размытия линий. Указанное обстоятельство позволяет для определения СК применить метод, описанный в /12/.
Представим два неперекрывающихся пятна размытия линий системы как квазимонохроматический, частично когерентный источник. Разобьём каждое пятно на ряд зон, параллельных направлению линий. Нумерацию зон проведем от точек идеального изображения линий. Выпилим две зоны с одинаковыми порядковыми номерами и рассмотрим СК излучения между точками этих зон. За начальную точку зоны примем ближнюю к идеальному изображению линии точку. Конечная точка определится как наиболее удаленная от идеальной в пределах зоны. Пусть интенсивность в пределах зон распределена по закону i(x). Распределение интенсивности в области дифракции Фраунгофера, обусловленное рассматриваемыми двумя зонами, обозначим i(р) . Тогда, если cК m
(х,х') рассматриваемых в пределах зон точек х и х' является пространственно-инвариантной функцией (m
(х,x') = m
(х- х') = m
(v)), то ее можно найти из соотношения /12/:
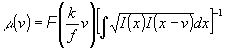 (5) (5)
где 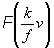 - Фурье-преобразование i(р). k - среднее волновое число, ¦
- фокусное расстояние Фурье-преобразующего объектива. Интегрирование в (5) ведется по общей области перекрытия функций i(x) и i(х – v). Представляя m
(v) в виде |m
(v)|exp[ij
(v)]. а - Фурье-преобразование i(р). k - среднее волновое число, ¦
- фокусное расстояние Фурье-преобразующего объектива. Интегрирование в (5) ведется по общей области перекрытия функций i(x) и i(х – v). Представляя m
(v) в виде |m
(v)|exp[ij
(v)]. а 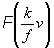 как как 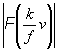 ·exp[iФ ·exp[iФ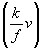 ] = ] = 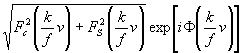 , вместо (5) получим: , вместо (5) получим:
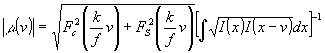 (6) (6)
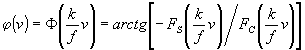 (7) (7)
Здесь 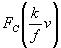 , , 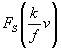 - соответственно, косинус- и синус-преобразование Фурье i(p). Таким образом, измеряя распределения i(x) и i(p), можно по (6), (7) найти модуль и фазу СК излучения между точками двух пятен размытая линий. Выделяя последовательно - соответственно, косинус- и синус-преобразование Фурье i(p). Таким образом, измеряя распределения i(x) и i(p), можно по (6), (7) найти модуль и фазу СК излучения между точками двух пятен размытая линий. Выделяя последовательно
- 54 -
различные зоны, можно найти |
m
(v)|
и j
(v) в разных зонах. Аппроксимируя значения |
m
(v)|
прямой, параллельной оси абсцисс, а j
(v) прямой, проходящей через рассчитанные точки таким образом, чтобы отклонение этих точек от прямой было минимальным, получим графики |
m
(v)|
и j
(v) в пределах каждой пары одноименных зон. На рис.1б для случая трех зон приведены в качестве примера получаемые таким образом графики |
m
(v)|
и j
(v). Разность фаз излучения между начальным точкам зон х0 и х0' принята равной нулю. В этом случае v = х'0 – х0. Максимальные значения разности фаз излучения в зонах j
i, j
ii, и j
iii определяются пересечением полученных прямых с вертикальной прямой, проходящей черев конечную точку зоны.
Данные о j
(v) можно использовать для нахождения функции j
а(u). Предположим, что оси координат графиков j
(u) параллельны и разность фаз начальных точек зон равна нулю. Тогда j
а(u) найдется по следующему правилу. Для её определения, совместив начальную точку второй зоны с конечной точкой первой, перенесем параллельно точки графика j
(v) второй зоны на величину (см.рис.1в). В этом случае точки 2 и 1 совместятся. Аналогично , начальную точку третьей зоны совместим с конечной точкой второй и сдвинем график j
(v) точек третьей зоны до совпадения точек 2 и 3. Максимальная фаза точек третьей зоны по отношению к начальной точке первой зоны определится тогда как j
i + j
ii + j
iii. Такие операции повторяются по числу рассматриваемых в пятне размытия зон. Данное правило следует из анализа функции j
а(u,u'), близкой по форме j
(u,u') и показанной на рис.1а. Рассмотрим сечения j
а(u,u') плоскостями, параллельными плоскости j
ou.. Согласно (4), в любой такой плоскости j
а(u) отличается от j
а(u) для u' = 0 на постоянную. Отсюда следует, что j
а(u) может быть получена путем сдвига на постоянные величины участков кривых j
a(u) из различных сечений. При рассмотрении точек зон равных порядковых номеров из всей совокупности значений j
а(u,u') выбираются только значения, соответствующие этим зонам. Так как в пределах двух выделенных зон j
(v), рассматриваемая как разность фаз СК излучения между начальной точкой зоны одного пятна и всеми точками другого, с точностью до постоянной
- 55 -
совпадает с j
a(u), то из вышесказанного следует правило нахождения j
а(u) по данным j
(v) для разных зон.
Информацию о j
а (u) системы рассеивающая среда-объектив можно получить более простым в экспериментальном отношении образом, анализируя картину дифракции Фраунгофера излучения от одного пятна размытия на щели. Действительно, так как j
(u) и j
(u') имеют одинаковую функциональную связь соответственно с u и u', то j
(u,u'), рассчитанная как разность фаз излучения между всеми парами точек в пределах одного пятна размытия, будет тождественно совпадать с j
(u,u'), полученной из анализа двух пятен размытая линий. Это обстоятельство позволяет при нахождении j
(u,u') заменить анализ фазы СК излучения точек двух пятен размытия линий на анализ фазы СК точек в одном пятне размытия. В этом случае, в пределах зоны j
(u,u') может рассматриваться как пространственно инвариантная. Если предположить, что модуль СК в пределах зоны постоянен, то j
(u - u') = j
(v) можно найти по (7), измеряя i(p). Заметим, что в этом случае х'0 – х0 = 0 и при расчетах v изменяется от нуля до величины, равной ширине зоны. Отметим также , что замена исследования СК излучения между точками двух различных пятен размытия на исследование СК в одном пятне не позволяет найти |
m
(u,u)|
. Для определения |
m
(u,u)|
в этом случае необходимо использовать другой, не зависимый от рассматриваемого, метод.
Данный способ определения j
a(u ) получил экспериментальное подтверждение. Находилась j
a(u) исследованной в /8/ системы среда-объектив при оптической толщине среды 9,5. В плоскость изображения линии устанавливалась щель шириной 14 мкм и с её помощью выделялись последовательно различные зоны. За щелью располагался объектив "Юпитер-8". Его фокальная плоскость и плоскость вели совпадали. За объективов помещался фотоумножитель с расположенной парод ним диафрагмой. Плоскость диафрагмы устанавливалась в другую фокальную плоскость объектива. Как известно /6/, поля комплексных амплитуд между двум фокальными плоскостями связаны преобразованием Фурье в одна фокальная плоскость объектива соответствует области дифракции Фраунгофера излучения на транспаранте, помещаемом в другой фокальной плоскости. Фотоумножитель с диафрагмой посредством микрометрического винта мог перемещаться перпендикулярно
- 56 -
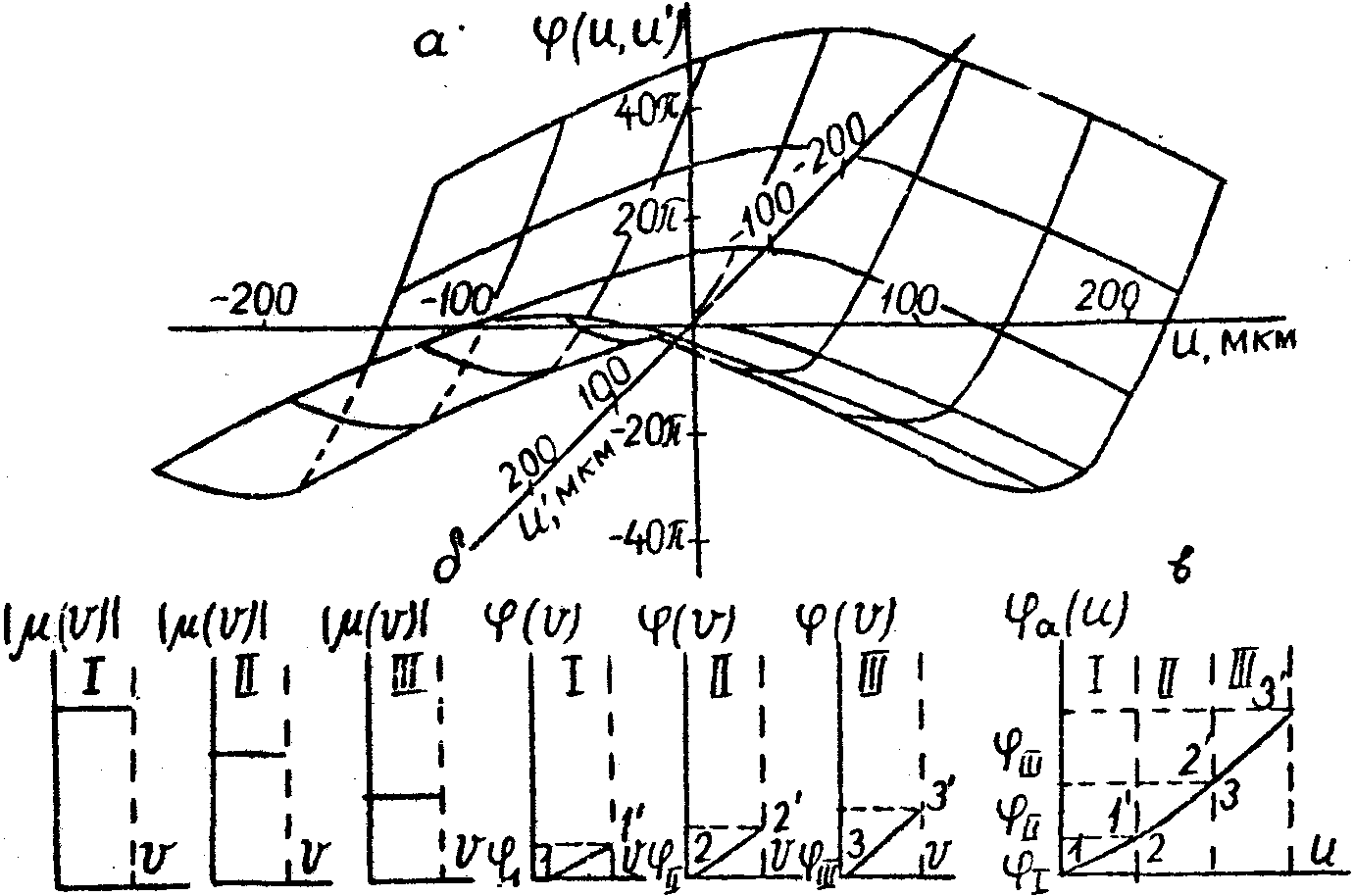
Рис.1. Фаза j
(u,u') ck-излучения между точками двух пятен размытия линии системы среда-объектив а); функции |m
(v)|
и j
(v) для разных зон (б) и построение функции j
а(u) по данным о j
(v) (в). Римские цифры - порядковые номера зон.
- 57 -
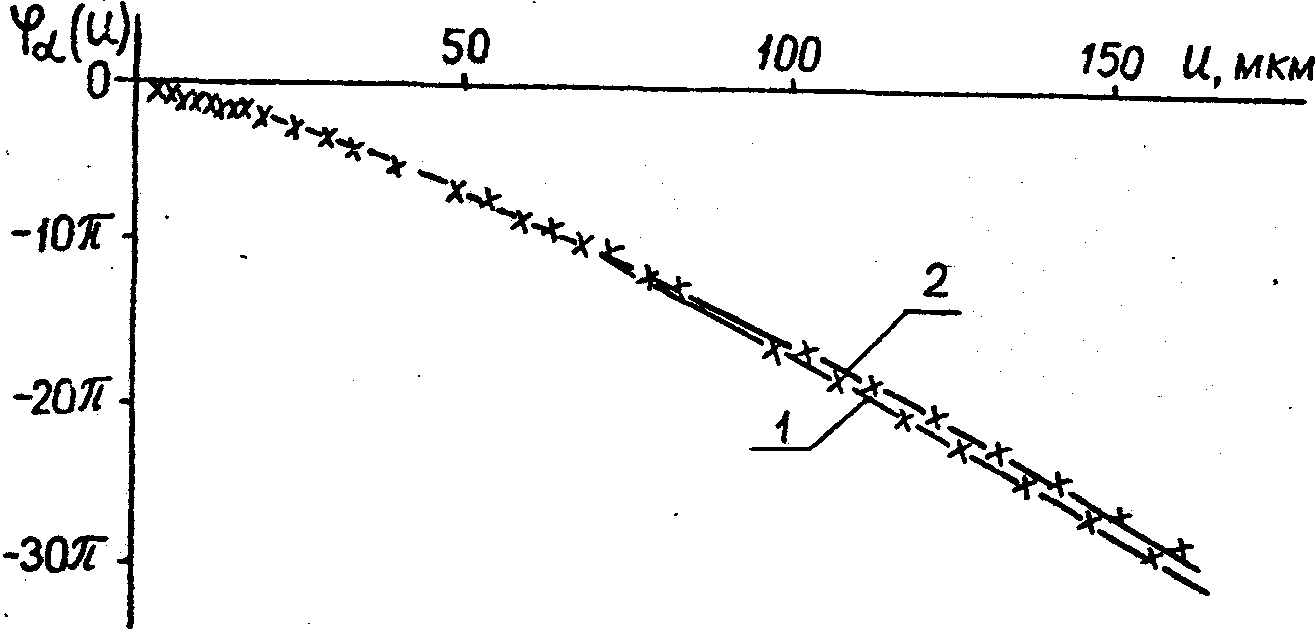
Рис.2. Значения (а) объектива (1) и системы среда-объектив (2), полученные из исследований картин дифракции. Значки - данные о j
(u), полученные интерферометрическим методом.
- 58 -
оптической оси системы. Сигнал с него усиливался и регистрировался потенциометром. По определяемым значениям i(р) по (7) рассчитывались j
(р) в каждой зоне. Общее число зон при исследовании половины пятна размытия равнялось 12. Для определения знака j
(v) применялось следующее правило. Знак j
(v) считался положительным, если при наблюдении со стороны объектива смещение выделяющей зоны щели вправо приводило к сдвигу максимума i(р) также вправо. Затем по данным о j
(v) указанным выше образом находилась j
a(v).
Н a рис.2 представлены данные о j
а(u) системы среда-объектив, а также о j
а(u) объектива, формирующего изображение вне рассеивающей среды, найденные аналогичным образом. Там же проведены значения j
(u), найденные интерферометрическим методом /10/. Как видно из рисунка, значения j
а(u) хорошо совпадают с j
(u). Совпадение наблюдается как для случаев формирования изображения объективом, так и системой среда-объектив. Таким образом, полученные результаты свидетельствуют о возможности определения СК излучения в пятнах размытия оптической системы из анализа картин дифракции Фраунгофера на щелях, помещаемых последовательно в разные участки пятен размытия. Этот способ может оказаться полезным при определении СК в системе среда-объектив в реальных условиях, когда использование интерферометрических методов затрудняется наличием вибраций системы.
Литература
1. П.А.Бакут, Н.Д.Устинов, И.Н.Троицкий, К.Н.Свиридов. Зарубежная радиоэлектроника, № 9, 3-30. 1976.
2. j.w.goodman, w.h.huntley et al. appl.phys.lett., 8, n12, 311-313, 1966.
3. j.d.gaskill. josa, 58, 5, 600-608, 1968.
4. a.w.lohmann, c.a.shuma. opt.communs., 7, n2, 93-97, 1973.
5. Е.В.Ивакин, А.И.Кицак. Оптика в спектроскопия. 53, вып.1, 99-102, 1982.
6. Р.Кольер. К.Беркхарт, Л.Лин. Оптическая голография.
- 59 -
М., "Мир", 688 с., 1973.
7. И.С.Клименко, Г.В.Скроцкий. Успехи физических наук, 109, № 2, 269-292. 1973.
8. К.Г.Предко, В.Г.Свнченко. Оптика и спектроскопия. 55, вып.1, 166-172, 1983.
9. М.Борн, Э.Вольф. Основы оптики. М., Наука, 720с., 1973.
10. Е.Г.Предко, В.Г.Синченко. Известия АН БССР, сер.физ., №6, 117-123, 1979.
11. А.П.Иванов. Физические основы гидрооптики, Минск. Наука ц техника, 504 с., 1975.
12. j.v.cornaocchio, r.p.soni. ii nuovo cimento, 38, 3, 1169-1177, 1965.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

