НАСЫЩЕНИЕ ИНТЕНСИВНОСТИ И УПРАВЛЯЕМОЕ ПРЕОБРАЗОВАНИЕ ВОЛНОВЫХ ФРОНТОВ ПРИ ВЫНУЖДЕННОМ РАССЕЯНИИ СВЕТА
Н.В.Окладников, В.В.Зверев, Г.Л.Бреховских, А.И.Соколовская
Исследуется влияние геометрических условий возбуждения на ход энергетических зависимостей Вp при возбуждении сфокусированным лазерным импульсом длительностью ~10-8 с. Геометрия опыта менялась путем использования линз с разными фокусными расстояниями, а также путем изменения глубины фокусировки пучка возбуждающего излучения в рассеивающую среду. Даётся теоретическая интерпретация экспериментальных результатов, которая базируется на квантовом рассмотрении явления ВКР в двухуровневой системе. Обнаруженные закономерности могут быть объяснены только при учёте выравнивания заселенностей уровней комбинационно-активного перехода. Результаты работы позволяют регулировать распределение интенсивности в спектре пространственных частот вынужденного рассеяния света.
В работах /1,2/, посвященных исследованию восстановления (обращения) волнового фронта света при вынужденном рассеянии (hp), было показано, что толщина слоя активной среды, играющего роль динамической голограммы, в значительной мере определяется распределением плотности мощности лазерного излучения вдоль рассеивающего объёма. В связи с поисками путей управления волновыми фронтами восстановленных при ВР пучков света большой интерес представляют экспериментальные исследования характера энергетической зависимости ВР от геометрических условий эксперимента.
В /3/ было экспериментально и теоретически показано, что при фокусировке возбуждающего излучения в рассеивающую среду наклон кривых энергетических зависимостей вынужденного комбинационного
- 36 -
рассеяния (ВНР) вперед зависит от фокусного расстояния линзы.
В настоящей работе были проведены экспериментальные исследования влияния на ход энергетической зависимости ВР величины фокусного расстояния линзы и глубины фокусировки накачки, т.е. расстояния от входной для накачки границы среды до геометрического фокуса линзы. Влияние глубины фокусировки на характер энергетических кривых ВР ранее не изучалось.
Источниками возбуждающего излучения служили рубиновый лазер с расходимостью »
3,5' и лазер на неодимовом стекле с расходимостью »
3'. Длительность лазерных импульсов – 2·10-8 с. В экспериментах возбуждалось вынужденное комбинационное рассеяние (ВКР) в жидком азоте и нитробензоле и вынужденное рассеяние Мандельштамма-Брилюэна (ВРМБ) в ацетоне и сероуглероде.
Били проведены измерения энергетических зависимостей ВКР вперёд и назад в жидком азоте и ВРМБ в ацетоне при возбуждении рубиновым лазером в слоях вещества существенно отличающейся толщины , но при одинаковой глубине фокусировки u и фокусным расстоянии линзы ¦
. Для возбуждения ВКР использовались кюветы с азотом толщиной ℓ =30 мм и 100 мм при ¦
=50 мм и u = 12 мм, для возбуждения ВРМБ - кюветы с ℓ = 20, 30 и 100 мм, ¦
= 50мм, u = 14мм. Полученные энергетические зависимости приведены на рис.1,2.
Как видно из рисунков, энергетические кривые для разных ℓ, но одинаковой глубины фокусировки практически совпадают. Отступление наблюдалось при больших мощностях накачки, когда расстояние от геометрического фокуса линзы до задней границы среды становилось сравнимым с длиной фокальной перетяжки (см. рис.2). Таким образом, при возбуждении ВР фокусированным пучком глубина фокусировки u является эффективной длиной, на которой происходит усиление ВР назад. Как показали наши эксперименты, увеличение глубины фокусировки при неизменных прочих условиях, приводит к возрастанию энергии рассеянного назад излучения как по абсолютной величине. так и по отношению к энергия излучения, рассеянного вперёд.
Результаты экспериментальных измерений энергии ВКР назад и ВРМБ в режиме насыщения в разных веществах и при различных сочетаниях ¦
и u приведены в таблице. В столбцах таблицы указаны: 1 - вид рассеяния и рассеивающее вещество; 2 - длина волны
- 37 -
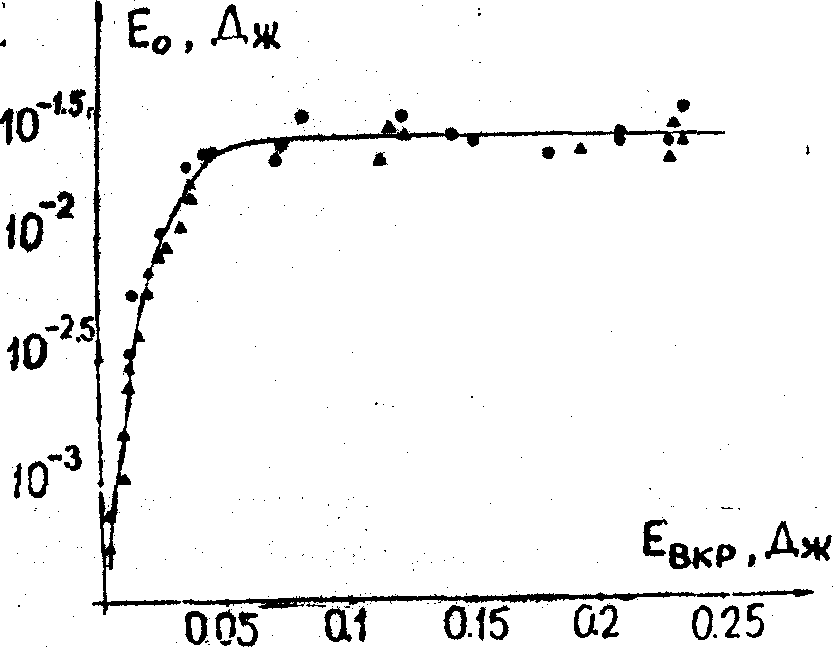
Рис.1. Энергетическая зависимость первой стоксовой компоненты ВКР назад в жидком азоте. ¦
=50мм, u = 12мм.
 ℓ = 30 мм. (ii)
ℓ = 30 мм. (ii)
 ℓ = 100 мм. (i)
ℓ = 100 мм. (i)
- 39 -
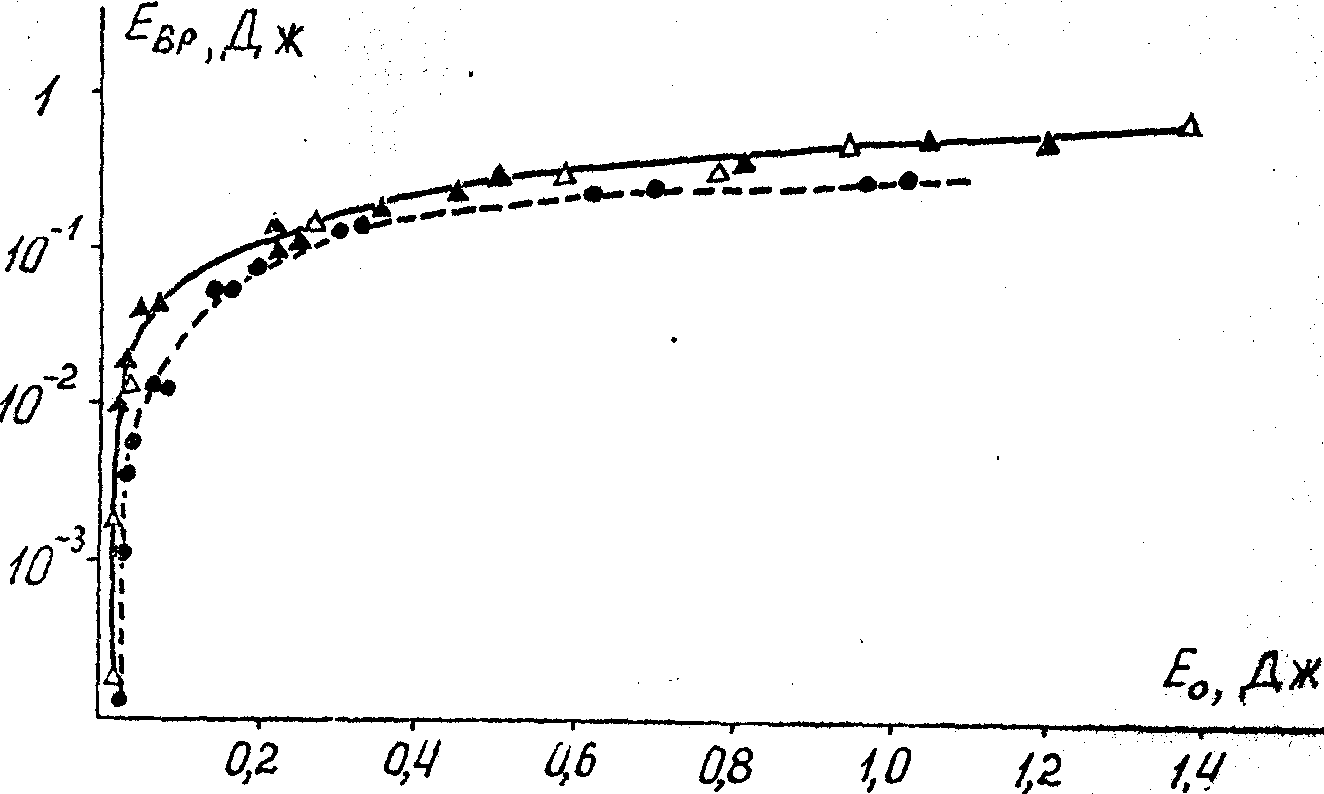
Рис.2. Энергетическая зависимость ВРМБ в ацетоне. ¦
= 50 мм, u = 14 мм.
 ℓ = 20 мм
ℓ = 20 мм
 ℓ = 30 мм
ℓ = 30 мм
D
- ℓ = 100 мм
- 39 -
возбуждающего излучения; 3 - фокусное расстояние линзы; 4 - глубина фокусировки; 5 - число измерений; 6 - интервал энергий накачки, в котором наблюдалось насыщение ВР; 7 - среднее значение энергии ВР в указанной интервале и среднеквадратичное отклонение отдельных измерений; 8 - изменение коэффициента преобразования энергии накачки в ВР в интервале D
Е0. Использовались кюветы толщиной 100 мм; диаметр пучка накачка в плоскости линзы составлял »
10 мм.
Таблица.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
l
0, мкм |
¦
, мкм |
u, мм |
nh |
Е0, мДж |
Есн, мДж |
r, % |
|
ВКР в жидком азоте |
0,69 |
50
100
100
230
280 |
12
24
42
50
48 |
13
9
9
9
6 |
60¸
240
350¸
1230
750¸
1600
370¸
710
310¸
710 |
25±
l
36±
2
47±2
92±2
112±
3 |
42¸
10
10¸
2,9
6,2¸
3,1
25¸
12,5
36¸
12,5 |
|
ВКР в нитробензоле |
0,69 |
100
280 |
31
62 |
7
6 |
140¸
385
550¸
850 |
14±
l
35±
2 |
10¸
3,6
6,4¸
4,1 |
|
ВРМБ в сероуглероде |
1,06 |
70 |
15 |
6 |
340¸
600 |
38±
1 |
11¸
6,3 |
При превышении энергией импульсов накачки определенной величавы Есн в наших экспериментах наблюдалось практически полное прекращение роста энергии ВР назад (полное насыщение). Как видно из таблицы, при увеличении энергии импульсов накачки в 2-3 раза отклонение энергии ВР от средней величину Есн не превышали нескольких процентов.
Прекращение роста энергии ВР назад в зависимости от сочетания ¦
и u наступало при различных коэффициентах преобразованиях
- 40 -
накачки в ВР, в том числе - сравнительно небольших (менее 10%). При дальнейшем увеличении энергии возбуждающего излучения коэффициент преобразования накачки в ВР уменьшался в обратной пропорции по отношению к Е0.
Уменьшение u при прочих равных условиях приводило к уменьшению энергии накачки, необходимой для достижения режима насыщения.
Энергия импульсов ВР назад для данного вещества, как видно из таблицы, в режиме полного насыщения примерно пропорциональна глубине фокусировки накачки в рассеивающий объем. В наших экспериментах величина отношения Есн/u для жидкого азота была 15-20 мДж/см, для нитробензола - »
5 мДж/см.
Энергия антистоксовых и высших стоксовых компонент ВКР назад в наших экспериментах составляла £
1% от энергии первой стоксовой компоненты. Полное прекращение роста ВКР назад не было связано с перераспределением энергии в пользу ВКР вперед. Например, при ВКР в жидком азоте (ℓ = 30 мм, ¦
= 100 мм, u=8 мм) наблюдалось полное насыщение энергии стоксовой компоненты ВКР как в направлении назад, так и вперед: в интервале энергий накачки 90¸
410 мДж энергия ВКР вперед составляла (19±
1) мДж. Полное насыщение ВКР вперёд в жидком азоте мы наблюдали и при несфокусированной накачке (диаметр пучка составлял »
1 мм); при использовании кюветы толщиной 30 мм в интервале D
Е0 130¸
350 мДж энергия ВКР вперед была (22±
1) мДж.
Интересно, что при возбуждении ВКР двумя импульсами накачки, разделенными по времени на »
10-4 с, суммарная энергия насыщения ВКР назад была равна энергии насыщения одиночных импульсов, а не удвоенной её величине.
ВКР световых импульсов длительностью »
10-8 с обычно описывается в предположении плоских волн системой связанных укороченных уравнений для интенсивностей накачки и первой стоксовой компоненты (напр., /4/):
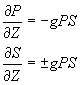 (1)
(1)
- 41 -
где Рб s - плотности потоков энергии возбуждающего и рассеянyоuо излучения, g - коэффициент усиления, знак "+" ("-") соответствует стоксовой волне вперёд (назад).
Систему (1) можно получить из квазистатического приближения более сложной системы укороченных уравнений, связывающих "медленные" амплитуды полей возбуждающей и стоксовой волн, колебательную координату и населенность основного уровня молекул /5/, если пренебречь дисперсией и изменением населенностей в процессе ВКР. Последнее кажется вполне оправданным при используемых интенсивностях накачки.
При небольших коэффициентах преобразования накачки в стоксовую волну (Р=const) остается уравнение ¶
s/¶
z = ±
gps, из которого следует, что интенсивность рассеянного излучения имеет экспоненциальную зависимость от интенсивности накачки и протяженности рассеивающей среды.
Когда интенсивность стоксовой волны по порядку величины сравнима с интенсивностью накачки, следует искать совместное решение системы (1). Теоретический анализ уравнений (1) /6-8/ показывает, что при увеличении интенсивности накачки первоначально экспоненциальный рост интенсивности ВР замедляется и переходит в линейный. Причиной насыщения ВР является истощение накачка вследствие перекачки значительной доли энергии в стоксову волну. Из решений такие следует, что в режиме насыщения интенсивность ВР на выходе на рассеивающей среды не зависит от толщины рассеивающего слоя. Коэффициент преобразования анергии накачки в ВР в отсутствие потерь в среде стремится к единице при возрастании интенсивности возбуждающего излучения.
Теоретическое описание ВР в предположении плоских волн возбуждающего и рассеянного излучения удовлетворительно объясняло экспериментальные результаты по исследованию ВР коллимированных световых пучков /8,9/. Качественное согласие с результатами эксперимента было получено также при использовании уравнений типа (1) для описания ВКР вперёд сфокусированного излучения /3/.
Однако, в рамках изложенной теоретический модели не могут быть описаны следующие результаты настоящей работы: 1) полное насыщение ВР, т.е. отсутствие зависимости интенсивности ВР от интенсивности
- 42 -
накачки; 2) наступление полного насыщения ВР назад в одном и том же веществе при различных значениях коэффициента пре-" образования накачки в ВР, в зависимости от фокусного расстояния линзы и глубины фокусировки; 3) возрастание энергии накачки, необходимой для насыщения ВР назад, при увеличении глубины фокусировки, т.е. эффективной толщины рассеивающего слоя; 4) пропорциональность энергии ВР назад в режиме насыщения глубине фокусировки накачки в рассеивающий объём.
Можно предположить, что насыщение ВКР при больших энергиях импульсов накачки объясняется выравниванием заселенностей уровней комбинационно-активного перехода. Рассмотрим элементарную теорию насыщения, основываясь на модели изотропного ВКР в двухуровневой среде, и покажем, что получающиеся зависимости интенсивности ВКР от интенсивности накачки и размера активной области качественно согласуются с экспериментально наблюдаемыми.
Следуя /10/, представим амплитуды стоксовой волны и волны накачки (имеющих, соответственно, частоты w
с, w
0 и волновые векторы 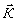 С,
С, 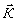 0), а также когерентную амплитуду молекулярных . колебаний в виде:
0), а также когерентную амплитуду молекулярных . колебаний в виде:
и запишем систему укороченных уравнений для медленно меняющихся амплитуд и связанные с ними уравнения для разности заселенностей в единице объёма (нормированное на одну частицу):
a'z + u-1ca't = 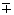 i(p
a
1nw
c/cnc)q*b (3)
i(p
a
1nw
c/cnc)q*b (3)
b'z + u-10b't = -i(p
a
1nw
0/cn0)qa (4)
q't + t-12(1 - iD
)q = -i(a
1c
2/2ħ)ba*n (5)
n't + t-11(n – 1) = -i(a
1/4ħ)(qb*a – к.с.) (6)
- 43 -
Здесь nc, n0 - показатели преломления и uc, u0 - групповые скорости для стоксовой и возбуждающей волн, соответственно, n - число частиц в единице объёма, Т1 - время релаксации колебательной энергия и t2 - время расфазировки; D
= t2(w
0 - w
с - w
к), где w
к - частота молекулярных колебаний. Верхний (нижний) знак в уравнении (3) (а также во всех последующих соотношениях, имеющих сдвоенный знак) соответствует рассеянию вперёд (назад), штрихаьш Обозначено дифференцирование. Входящая в (3-6) константа a
1 определяется членом энергии взаимодействия (1/2·a
1Е2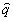 ), линейным по оператору
), линейным по оператору 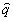 координаты молекулярного осциллятора, матричный элемент этого оператора обозначен c
.
координаты молекулярного осциллятора, матричный элемент этого оператора обозначен c
.
Для наиболее широко используемого в наших экспериментах вещества, жидкого азота, время релаксации Т1, измеренное методом некогерентного антистоксова рассеяния пробного импульса, составляет »
1,5 с /11/; по времени затухания люминесценции молекул СО, наводящихся в смеси с n2 – t1 »
56 с /12/; время расфазировки t2, измеренное по методу kapС - »
1,5·10-10 с /13/. Таким образом, при длительностях возбуждающих импульсов Т ~ 10-8 с выполняется неравенство Т1 > Т >Т2, что позволяет пренебречь релаксацией со временем Т1 и заменить уравнения (3-5) на соответствующие стационарные уравнения (квазистатическое приближение /5/). Вводя плотность потоков энергии
s = cnc|
a|
2/8p
; p = cn0|
b|
2/8p
(7)
и исключая q, получим из (3-6) систему уравнений:
(w
c/w
0)p'z = 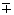 sz = (ħw
cn/2)n't = -g
psn (8)
sz = (ħw
cn/2)n't = -g
psn (8)
где
g
= 8p
2w
ca
21c
2nt2/ħn0ncc2(1 + D
2) (9)
Будем полагать, что уменьшение интенсивности возбуждающей волны, связанное с перекачкой энергия в стоксову волну, пренебрежимо мало, так что p=const. В результате получим нелинейную систему уравнений в частных производных, сводящихся подстановкой
- 44 -
w = ln(sn) к уравнении Лиувилля:
w"zt = 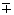 (4g
2p2/ħw
cn)exp(w) (10)
(4g
2p2/ħw
cn)exp(w) (10)
Точное решение уравнения (10) хорошо известно и приводится, к примеру, в работе /14/. Соответствующее решение интересующих нас уравнений может быть найдено путем подстановки
n = 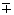 (g
pj
)-1j
'z; s = (ħw
cn/2g
pj
)j
't (11)
(g
pj
)-1j
'z; s = (ħw
cn/2g
pj
)j
't (11)
сводящей решение системы к решению уравнения Даламбера: j
"zt = 0. Как известно, решение последнего имеет вид: j
= g(t) + f(z), где g и f - произвольные функции. Для отыскания этих функций сформулируем начальные и граничные условия.
Будем считать, что при z = 0 имеется источник затравочного излучения стоксовой волны с неизменной плотностью потока энергии: s(0,t) = s0. Кроме того, предположим, что в начальный момент времени t =0 в объёме, заполненном активной средой, установилось квазистатическое распределение поля, соответствующее наибольшему усилению волны в каждой точке; s(z,0)=s0exp(±
g
pz), при этой нормированная разность заселенностей в любой точке максимальна и равна n(z,0) = 1. Представим окончательное решение в виде:
s = -s0rexp(2g
ps0t/ħw
cn), n = rexp(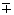 g
pz) (12)
g
pz) (12)
где r = (1 – exp(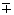 g
pz) – exp(2g
ps0t/ħw
0n))-1.
g
pz) – exp(2g
ps0t/ħw
0n))-1.
Считая импульс накачки прямоугольным, усредним интенсивность стоксовой волны по длительности импульса. Обозначим ℓ протяженность активной области вдоль оси oz и вычислим значение средней интенсивности при z = ℓ (при z = -ℓ) в случае рассеяния вперёд (назад):
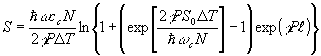 (13)
(13)
Заметем, что при малых энергиях импульса накачки РD
Т за время действия импульса разность заселенностей не успевает измениться
- 45 -
существенным образом. Этот предельный случай получается из (13) при РD
Т ®
0 и соответствует экспоненциальному закону усиления, наблюдаемому вблизи порога ВКР: s = s0ехр(g
Рℓ). В противоположном предельном случае больших Р, соответствующем области насыщения. из (13) следует:
s = ħw
cnℓ/2D
t + s0 (14)
При больших Р энергия импульса bkp sD
t перестает зависеть от Р и линейна по ℓ.
Таким образом, сопоставление результатов экспериментальных исследований и элементарной теории ВКР показывает, что при возбуждении ВКР импульсами наносекундной длительности выравнивание населенностей уровней комбинационно-активного перехода, по-видимому, оказывает значительное влияние на рост интенсивности рассеянного света м может привести к полному насыщению ВКР.
Результата настоящей работы интересны с точки зрения поиска новых путей управления процессами восстановления и преобразования волновых фронтов при КР света. Согласно /2/, при сфокусированной накачке разные области объёма рассеивающей среды играют различную роль в процессе передачи информации полю ВР. В области среды, прилегающей к фокусу линзы, прежде всего наступает полное насыщение ВКР. Экспериментальные исследования показали, что именно в этой области происходит формирование интенсивной когерентной волны ВР, которая во направленности близка к наиболее интенсивной составляющей поля возбуждающего света. Полное воспроизведение сложной амплитудно-фазовой структуры поля накачки происходит при дифракции этих волн на неоднородностях усиления в области экспоненциального роста ВР /15/. Эти области обычно располагаются вблизи окон кюветы, где плотность скорости накачки минимальна.
В случае, когда полное насыщение ВР имеет место во всем рассеивающем объёме, передача полной информации о фазе накачки возможна только, когда глубина модуляции интенсивности возбуждающего излучения равна 1, например, при фокусировке в рассеивающую среду изображения амплитудного транспаранта /16/. Проведённые исследования показали, что дифракционная эффективность усиливающей голограммы
- 46 -
существенно зависит от энергии считывающей волны ВР (см. рис.3). Варьируя длину области полного насыщения ВР в среде, можно управлять дифракционной эффективностью голограммы, что позволяет осуществлять необходимые преобразования волновых фронтов при вынужденных рассеяниях света. Например, повышение дифракционной эффективности голограммы создает наиболее благоприятные условия для восстановления в поле ВР пространственных частот внешних порядков. В результате на частоте ВР производится волновой фронт возбуждающего излучения с преобладанием угловых гармоник высшего порядка, интенсивность которых по отношению к нулевой гармонике может быть значительно больше, чем в поле накачки.
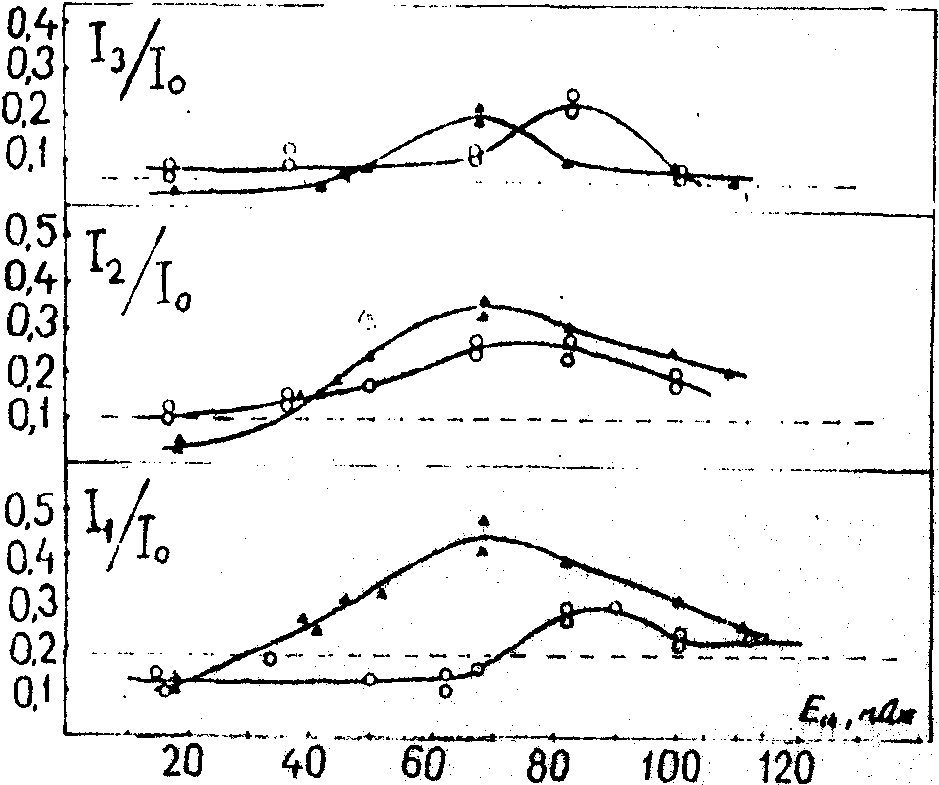
Рис.3. Отношение интенсивности высших порядков дифракции ВР (in) к интенсивности нулевого порядка (i0) в зависимости от энергии считывающего пучка (Есч).
- 47 -
Литература
1. Бреховских Г.Д.. Соколовская А.И., Окладников Н.В. Мaт. xi Всес. школы по голографии, Л., ЛИЯФ, 1979.
2. Бреховских Г.Л., Окладников Н.В., Соколовская А.И. ЖПС, 32, с.24, 1980.
3. Зубов В.А., Крайский А.В., Сущинский М.М., Федянина М.И., Щувалов И.К. ЖЭТФ, 59, с.1466, 1970.
4. shen y.r., bloembergen k. phys.rev., 137А, 1787, 1965.
5. Ахманов С.a., Драбович, К.И., Сухоруков А.П., Чиркин А.С. ЖЭТФ, 59, с.485, 1971.
6. culver w.h., soppy e.j. j.appl.phys., 35, 3421, 1964.
7. Зубов В.А., Сущинский М.М., Щувалов И.К. ЖПС, 3, с.336-341, 1965.
8. tang С.l. j.appl.phys., 37, 2945, 1966.
9. uhfc.r a.3., Зубарев И.Г., Мишин В.М., Смирнов В.Г. Препринт ФИАН. № 14, 1973.
10. Ахманов С.А., Коротеев ii. И. Методы нелинейной оптики в спектроскопии рассеяния света. М., 1981.
11. calaway w.f. and ewing g.e. chem. physics lett., 30, 485, 1975.
12. brueck s.r.j. and osgood r.m.jr. chem. physics lett.. 39, 568, 1976.
13. laubereau a. chem.phys.lett., 27, 600, 1974.
14. Барбашов Б.М., Нестеренко В.В.. Червяков А.М. ТМФ, 40, с.15, 1979
15. Соколовская А.И., Бреховских Г.Л. ДАН СССР, 243, с.630-633. 1978.
16. Окладников Н.В., Дробинин С.Ю. Бреховских Г.Л., Соколовская А.И., Ферье Ж., by 3., Ривуа Ж. Мат. Хiv Всес. школы по когерентной оптике и голографии. Л., 1982.

